math
The artistic and the mathematical mind are not so far apart.
Physicist Don Lincoln explains why mathematics is a powerful tool for scientific modeling, but is not a science itself.
An extraordinary haberdasher obsessed with buttons, lace collars, and death pioneered modern statistical analysis during the Age of Reason.
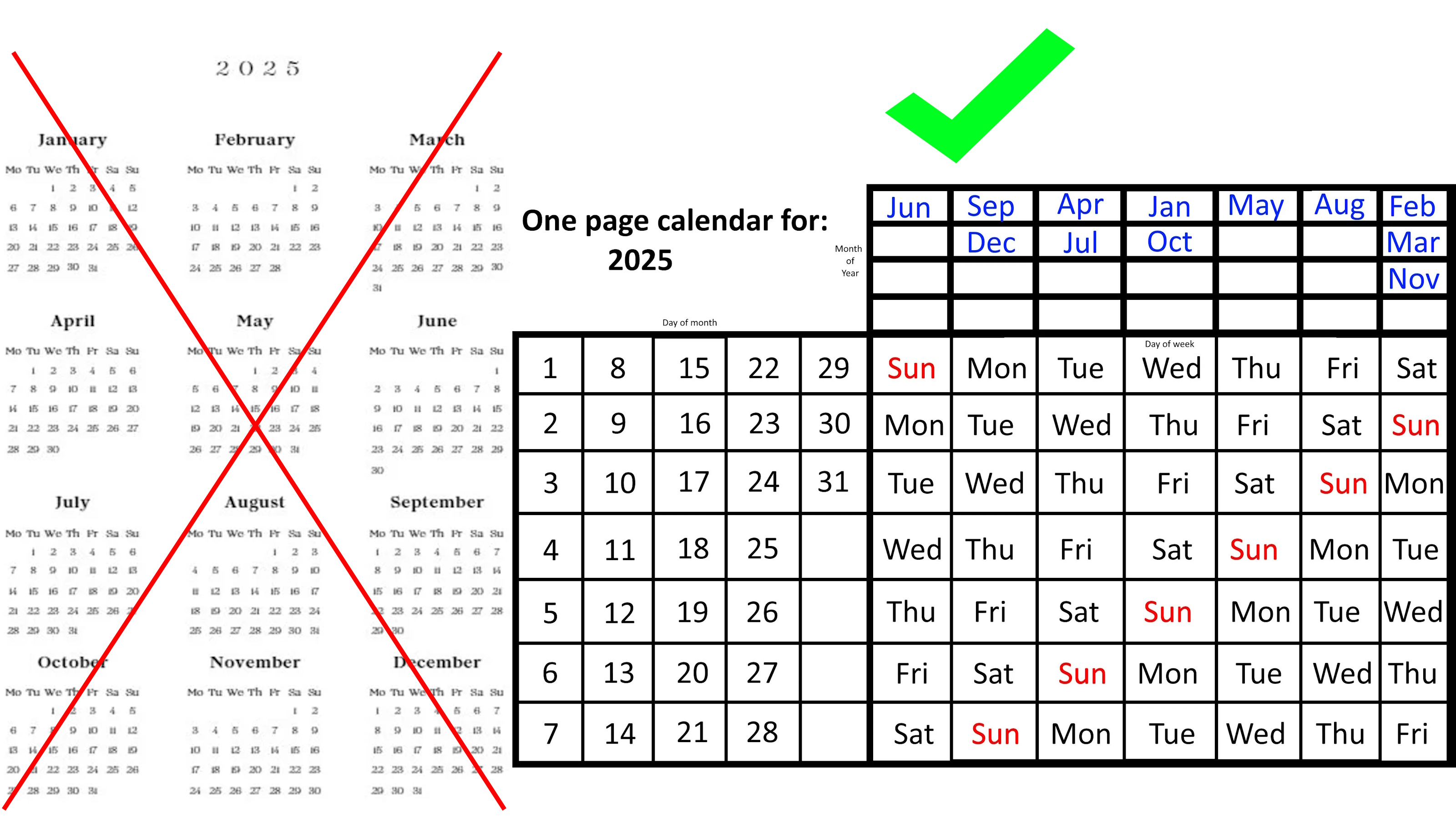
It’s simpler, more compact, and reusable from year-to-year in a way that no other calendar is. Here’s both how it works and how to use it.
On larger and larger scales, many of the same structures we see at small ones repeat themselves. Do we live in a fractal Universe?
How black and white is your thinking?
The secret sauce is the real world.
Are breakthroughs really a matter of chance, or are they simply waiting to be uncovered by the right person at the right time?
From nothing to everything: How zero changed our understanding of the universe, forever.
▸
3 min
—
with
Statistician Talithia Williams on how math is the clearest path to understanding our existence.
▸
3 min
—
with
Why dispelling the notion that it’s all about getting the correct answer is so powerful.
The all-time record is Usain Bolt’s 9.58 seconds, set in 2009. What is the fastest time, ultimately, for an ideal human body?
It’s knowledgeable, confident, and behaves human-like in many ways. But it’s not magic that powers AI though; it’s just math and data.
Holograms preserve all of an object’s 3D information, but on a 2D surface. Could the holographic Universe idea lead us to higher dimensions?
A human hand has the power to split wooden planks and demolish concrete blocks. A trio of physicists investigated why this feat doesn’t shatter our bones.
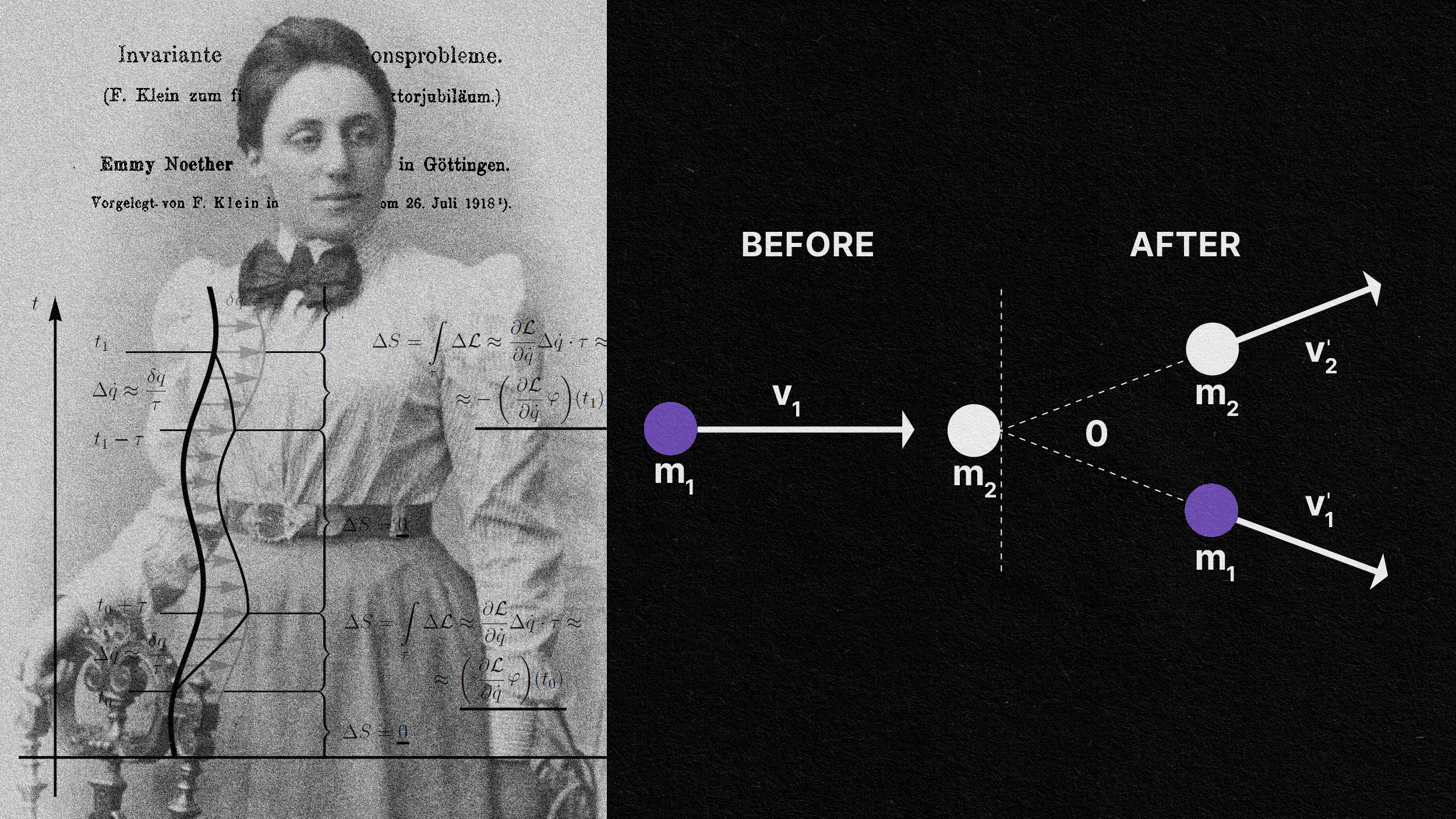
First derived by Emmy Noether, for every symmetry a theory possesses, there’s an associated conserved quantity. Here’s the profound link.
Even if you aren’t in the path of totality, you can still use the solar eclipse to measure how long it takes the Moon to orbit Earth.
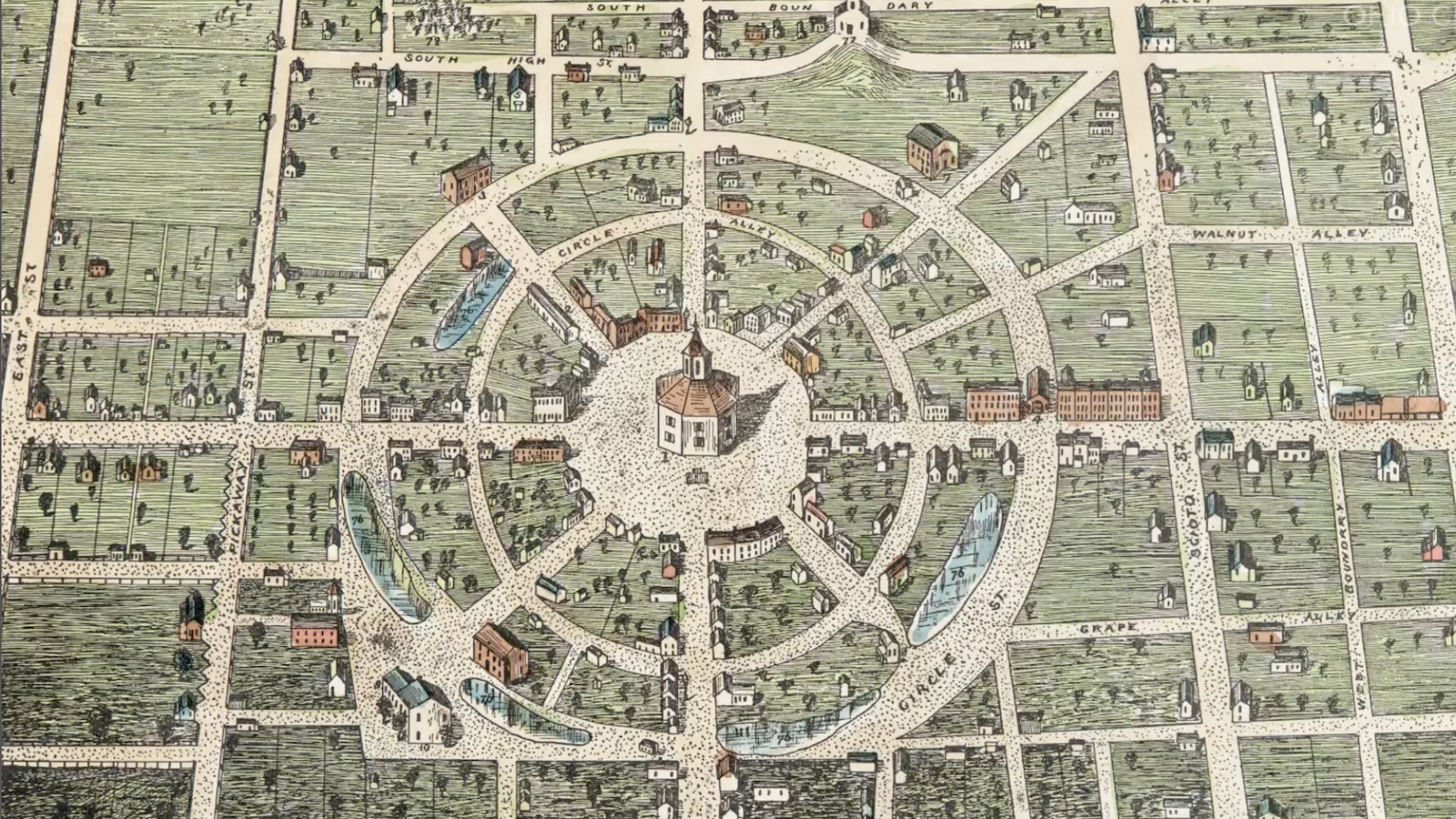
A small Ohio town tried to escape America’s addiction to rectangular grids. It didn’t last long.
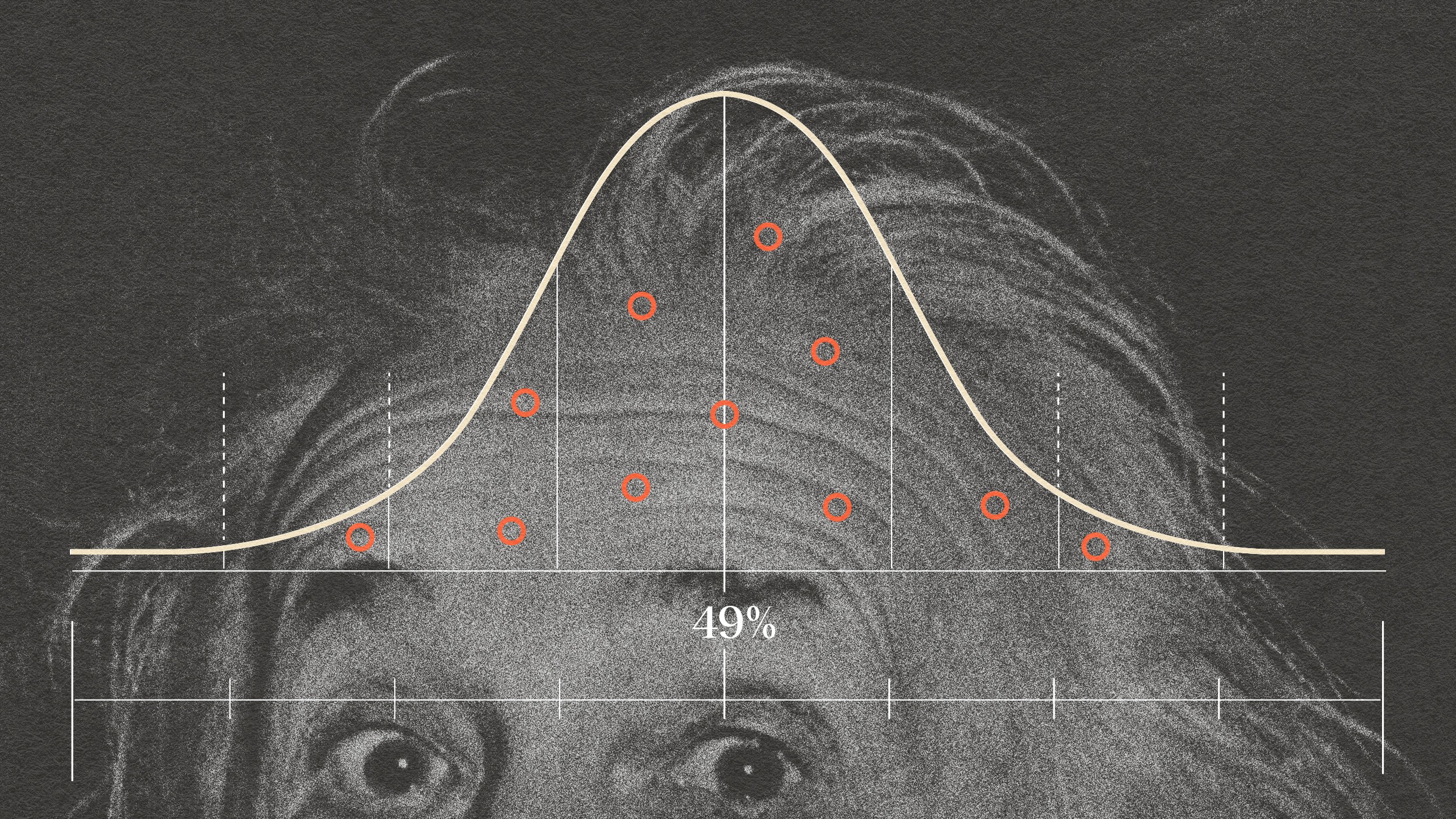
Almost everything we can observe and measure follows what’s known as a normal distribution, or a Bell curve. There’s a profound reason why.
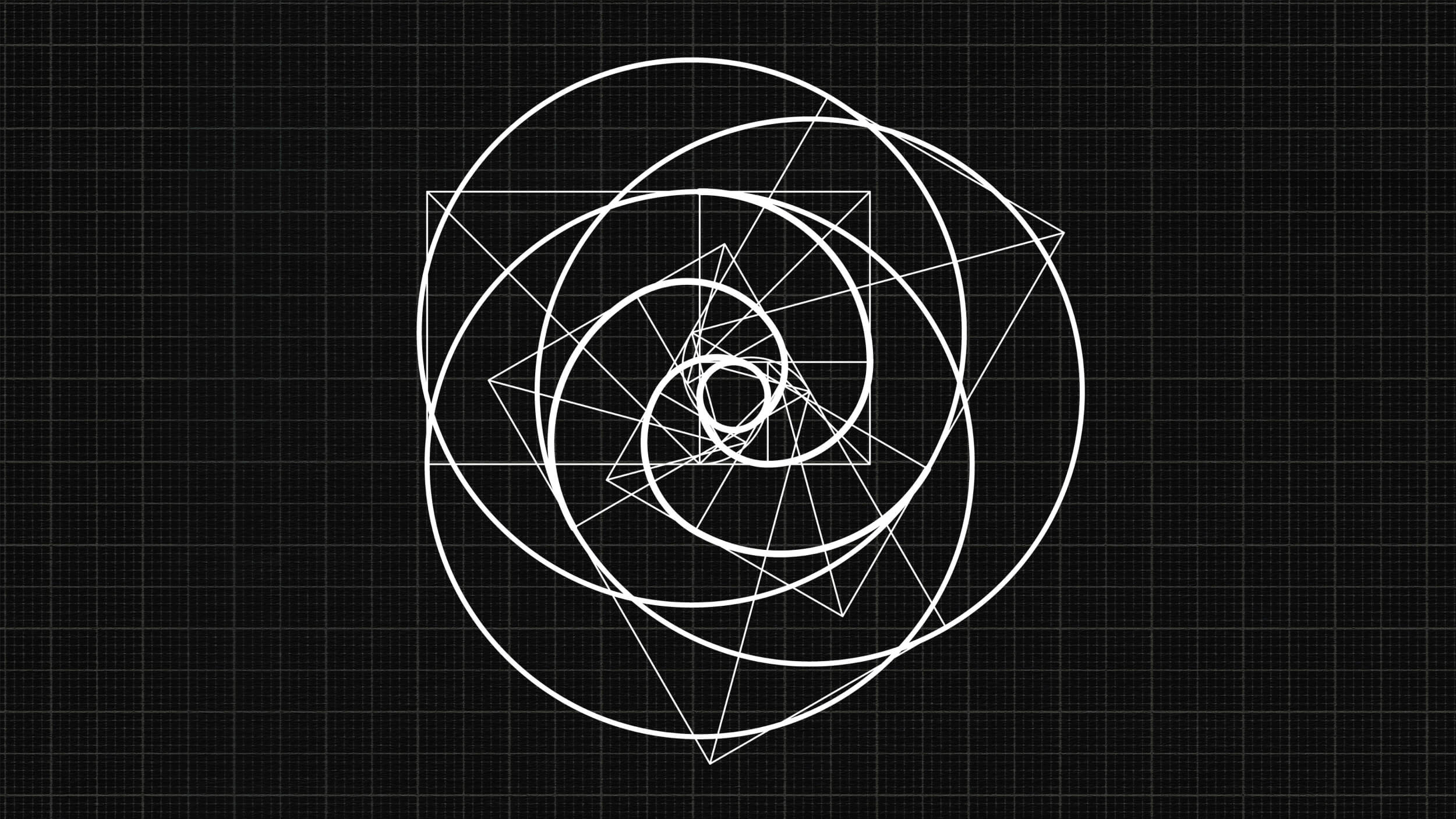
The pattern 1, 1, 2, 3, 5, 8, 13, etc., is the Fibonacci sequence. It shows up all over nature. But what’s the full explanation behind it?
Each time you fold a piece of paper, you double the paper’s thickness. It doesn’t take all that long to even reach the Moon.
In pre-War Cambridge, students had to ace an interview with Ludwig Wittgenstein to attend his lectures — Alan Turing passed that test, and went on to create one of his own.
While ice itself is slick, slippery, and difficult to navigate across under most circumstances, skaters easily glide across the ice.
A woman’s name would undermine the credibility of the mission. Names of former Nazis, however, were no problem.
Yes, you CAN be a “math person” — as long as you follow these learning techniques.
▸
4 min
—
with
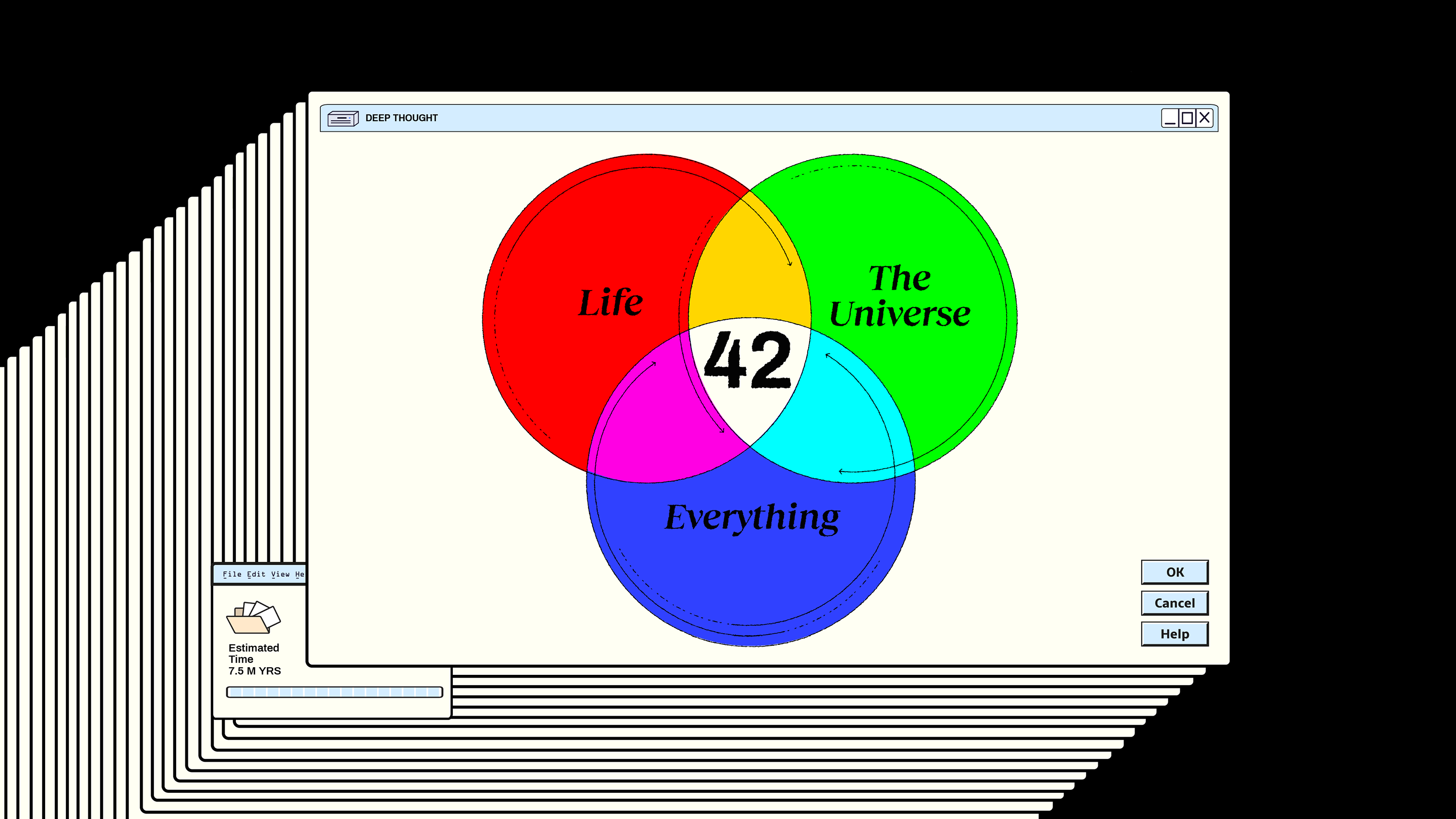
Although we still don’t know the question, we know that the answer to life, the Universe, and everything is 42. Here are 5 possibilities.
The smartest person in the world was Isaac Newton, a true polymath whose brilliance never has been, nor ever will be, surpassed.
They’re not just watching you; they’re also calculating.
How can you maximize the amount of love and happiness in your life? One of history’s greatest scientists found the answer: with math.
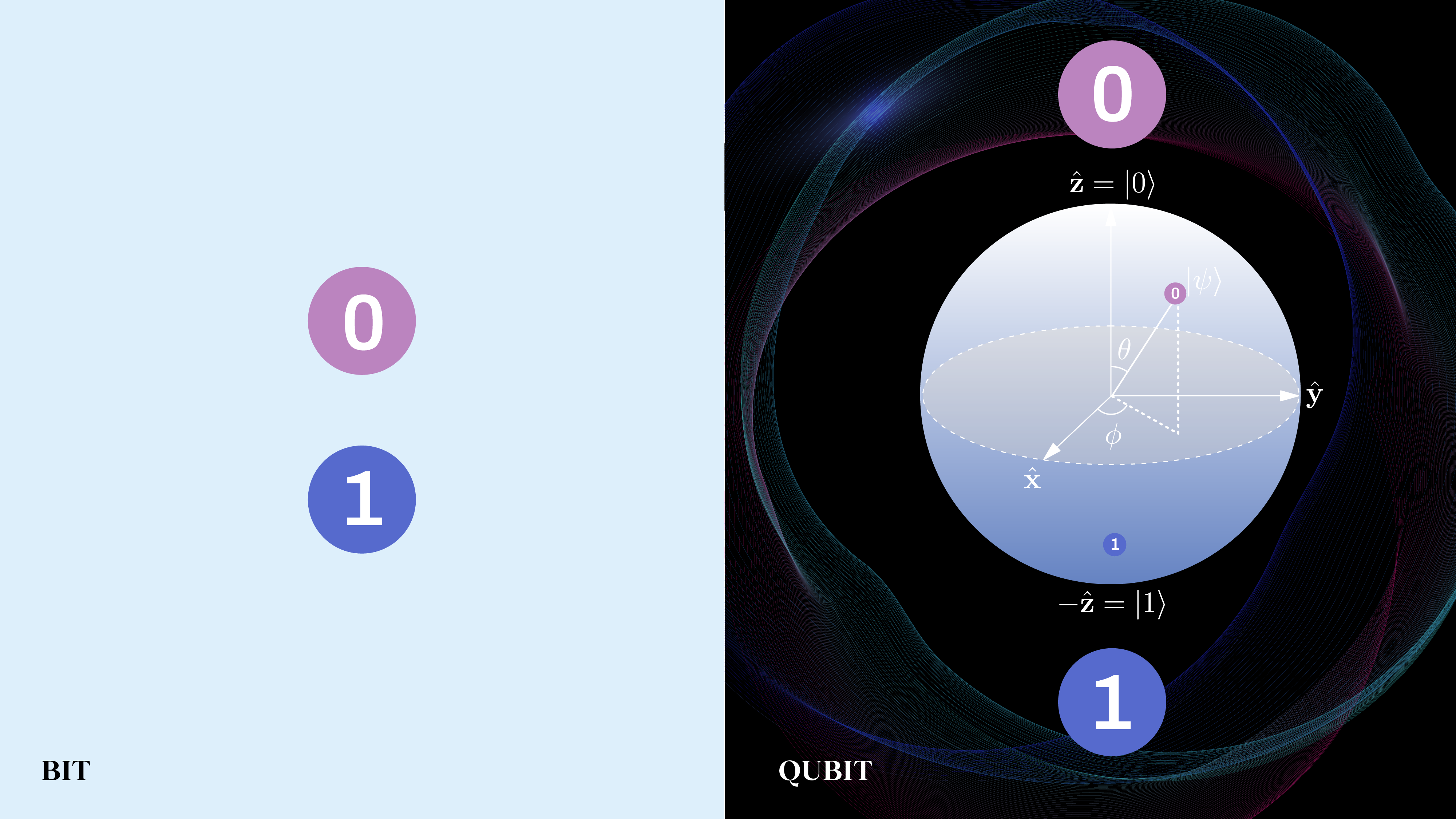
Can quantum computers do things that standard, classical computers can’t? No. But if they can calculate faster, that’s quantum supremacy.