Astronomer Johannes Kepler solved life’s hardest problem: marriage

- Although he's most famed for his laws of planetary motion and the discovery of heliocentric, elliptical orbits, Kepler solved another great problem: marriage.
- In choosing which person to marry, Kepler recognized that both waiting too long and choosing too early led to suboptimal outcomes.
- Through the power of mathematics, he figured out a simple rule: reject the first 37% of all potential marriage partners, then pick the next "best" one. His solution still holds up today.
One of the greatest scientists of all-time, Johannes Kepler, is most famed for being the first to correctly describe the motion of the planets around the Sun. Prior to Kepler, the geocentric model of our Solar System held sway, as its predictions were superior to the heliocentric ones of Copernicus. But Kepler came along and, after initially constructing his own heliocentric model with circular orbits for the planets, abandoned it in favor of a model that better fit the data: one with elliptical orbits instead of circular ones. More than 400 years later, his three laws of planetary motion are still taught and studied all across the world.
However, Kepler also used his mathematical prowess to solve a very different terrestrial problem that many of us still face in our lives here on Earth: when is the optimal time to marry someone, assuming you want to maximize the happiness in your life? The answer, perhaps surprisingly, is to follow what’s known as the 37% rule: reject the first 37% of all possible choices, and then pick the very next one to come along whose potential exceeds the best of the 37% who came before. Although some will wind up passing over their optimal choice and others will choose a partner before ever meeting their best possible match, the 37% rule is the mathematically superlative strategy. Here’s the science behind why.

The marriage puzzle
To be clear, the marriage puzzle that we’re talking about is the puzzle as it applied in Kepler’s day, not as it is today. Whereas today, divorce is common, open/polyamorous relationships are not shunted to the fringes of society, and choosing a new partner isn’t stigmatized in the same way, Kepler’s idea of marriage was more akin to an enormous, irrevocable decision. Back in Kepler’s day, many things were true that are no longer true today, including:
- You had to marry someone before you could truly spend enough time with them to know what life with them would be like.
- Marriage was a one-time proposition: once you married someone, you would be “stuck” with them until you died.
- And marriage meant the exclusion of all other potential partners once you made your selection.
Even though, of course, this is not exactly how marriage worked in practice, the concept of the puzzle — where you can peruse many options and say yes/no to everyone, but once you make your choice, it’s yours to live with forever and you never get to choose again — is very similar to a myriad of choices that many of us will face over the course of our lifetimes.

The way to think about this puzzle, from a mathematical point of view, is that you can imagine there’s some way of measuring your outcome — happiness, in this case — with each of your potential choices. You don’t know what the maximum possible value of your outcome is; you’re only capable of “ranking” the potential candidates according to your own experiences and perceptions. However, it’s very clear that there are two major potential pitfalls that can occur when having to make a big decision in life where you only get one chance that you’ll have to live with forever after.
- You can choose the first “good” thing that comes along and try to be content with that. Although this will give you an outcome where you (supposedly) have more happiness in your life than if you didn’t ever choose anything at all, choosing something too soon means you run the risk of being unable to choose a better option if one should come along again later.
- Or, you can reject the early candidate options that come along in the beginning, waiting until an incredible option comes along that simply blows away everything previous that you had to consider. The downside here is that your potentially optical choice might be “front-loaded” in your experience, and if you wait for someone to surpass that option, you might wind up alone, as that option may never present itself to you.

So, all other things being equal, what should your strategy be when faced with a situation like this:
- where you get one choice among many different candidates,
- where you must either say “yes” or “no” to each option shortly after encountering it,
- where you don’t get to test various options out at once or return to a previous option after rejecting it,
- and where once you decide “yes” to any option, the game is over?
Believe it or not, the answer for arriving at the optimal strategy doesn’t depend on many of the things you might expect it would. It doesn’t depend on how much happiness you see in your future with the first option that comes along. It doesn’t depend on when, assuming you reject the first option, a better option than that first one comes along? It doesn’t depend on what the difference is between your “best” and “worst” option among the first several candidate choices. And it doesn’t depend on the amount that your “best” option, so far, outpaces all of the other options that you encountered.
The only thing your answer should depend on, from a mathematical point of view, is knowing how many potential options you’re likely to encounter over the relevant timeframe.

The solution
Isn’t that a weird bit of information? But statistically, it’s absolutely true: as long as you know the total number of “options” you’ll be presented with, then your strategy for how you should make your choice is determined solely by that. Assuming that the candidates will appear to you in random order, without any bias given to “when” you’re most likely to see your most preferred outcome(s), the answer is as follows.
- No matter how much you like any of the early options that are presented to you, you should unilaterally reject the first 37% — technically, the first 36.788% — of all options that you encounter.
- However, you should remember, honestly and without either rose-colored glasses or sour grapes, what the best option you’ve seen so far is, and that should serve as your standard for comparison.
- Then, the very next time you encounter an option that you deem is superior to that previous “best option” you remembered, you should choose that option and never look back.
Although you’ll still have a chance at a bad outcome, where either a better candidate comes along than the option you’ll wind up choosing or no superior candidate to the one you rejected earlier ever emerges, this strategy will maximize your chances of choosing the best possible option you’ll encounter in your life.

You might be wondering, exactly, what it is that’s so special about the number “37%” or “36.788%” if you want to get more precise?
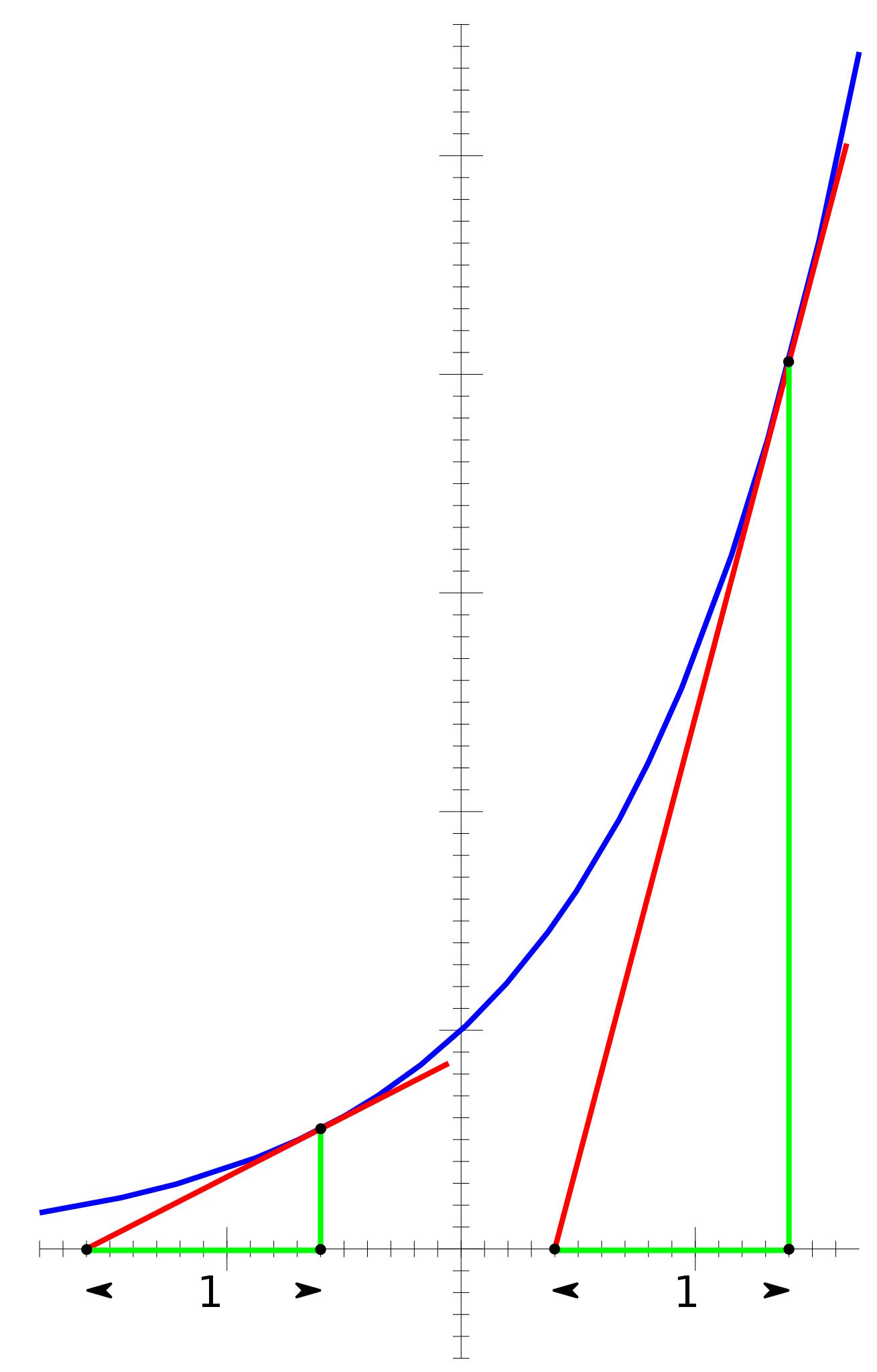
While the most famous transcendental number of all time is π, or 3.14159265358979323846… (and so on), the second most famous transcendental number is one that many of you will have encountered before in mathematics: e. Whereas π is the ratio of a circle’s diameter to its circumference, the mathematical e, approximately 2.718281828459…, is definable in a number of important ways.
- It’s the only positive number that you can graph exponentially, where y = ex, whose slope is 1 at x = 0.
- It’s the base of natural logarithms, where taking the natural log of e = 1.
- It’s the fundamental constant e that appears in the famous Euler identity: where eiπ + 1 = 0.
- And it’s the only natural exponential function whose derivative equals itself: the derivative of ex is also ex.
It also just happens to be, mathematically, involved in the solution to this exact sort of problem. However many candidates you have to consider, you should unilaterally reject the first 1/e fraction of candidates (where 1/e = 0.36787944117…), and then choose the first option that’s better than the best of the options you rejected. It’s not just science, it’s math.
What are your odds of getting the best outcome?
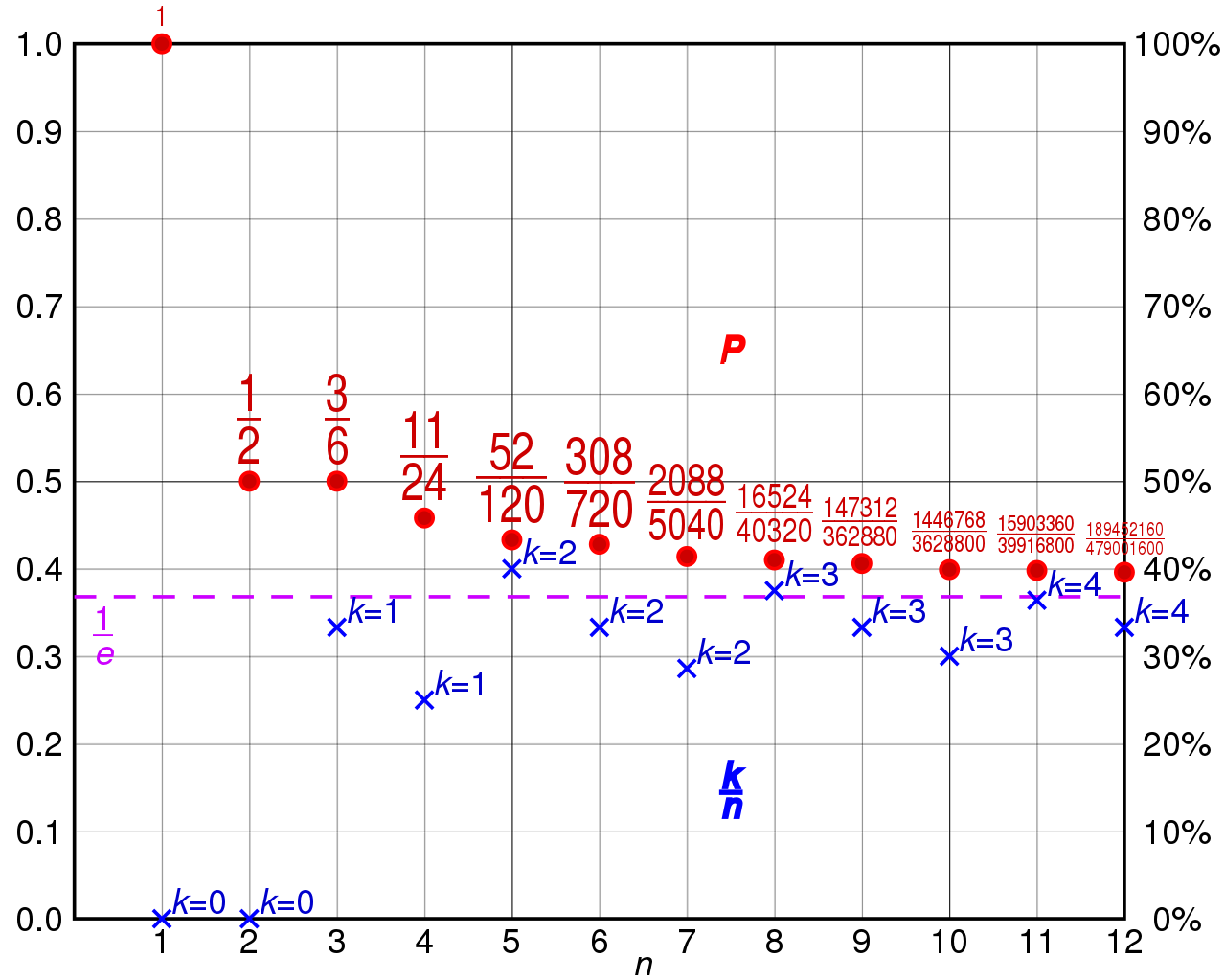
This is a very fun little “part II” to the question: assuming you choose the optimal strategy for attacking this problem — rejecting the first 1/e (or 36.788%) candidate options and then choosing the first option that exceeds the best option you saw over that initial time — what are the odds that you will actually wind up selecting the overall best possible option?
The answer, believe it or not, is also 1/e, or 36.788%. The breakdown of why is as follows.
- If the best option for you, overall, was actually in that first “1/e” or 36.788% of possible options that were presented to you, then you’ve already rejected them, and there’s no chance of choosing them. Simply by adopting this strategy, you’ve opened yourself up to the possibility that the set of options you sampled and threw away contained the best choice.
- Therefore, there’s a “1 – 1/e” or 63.212% chance that you will actually encounter an option that exceeds the value of your “best possible choice” in the set you sampled, meaning that there’s a 63.212% chance that you’ll do better than if you had selected the best from among your early options.
- However, assuming you chose the “best option” you encountered after rejecting the first 36.788% of candidate options, you will very likely have additional options remaining to consider. If you work out the math, it turns out that the odds of the true “best option” being in the set of candidates you do not get to see is “1 – 2/e,” or ~26.424%.
Because 63.212% – 26.424% actually equals 36.788%, which is 1/e, that turns out to be the probability of choosing the optimal outcome. It’s mathematically provable that no other strategy will equal or exceed a 1/e, or 36.788%, chance of obtaining the best outcome.
Did Kepler really have anything to do with it?
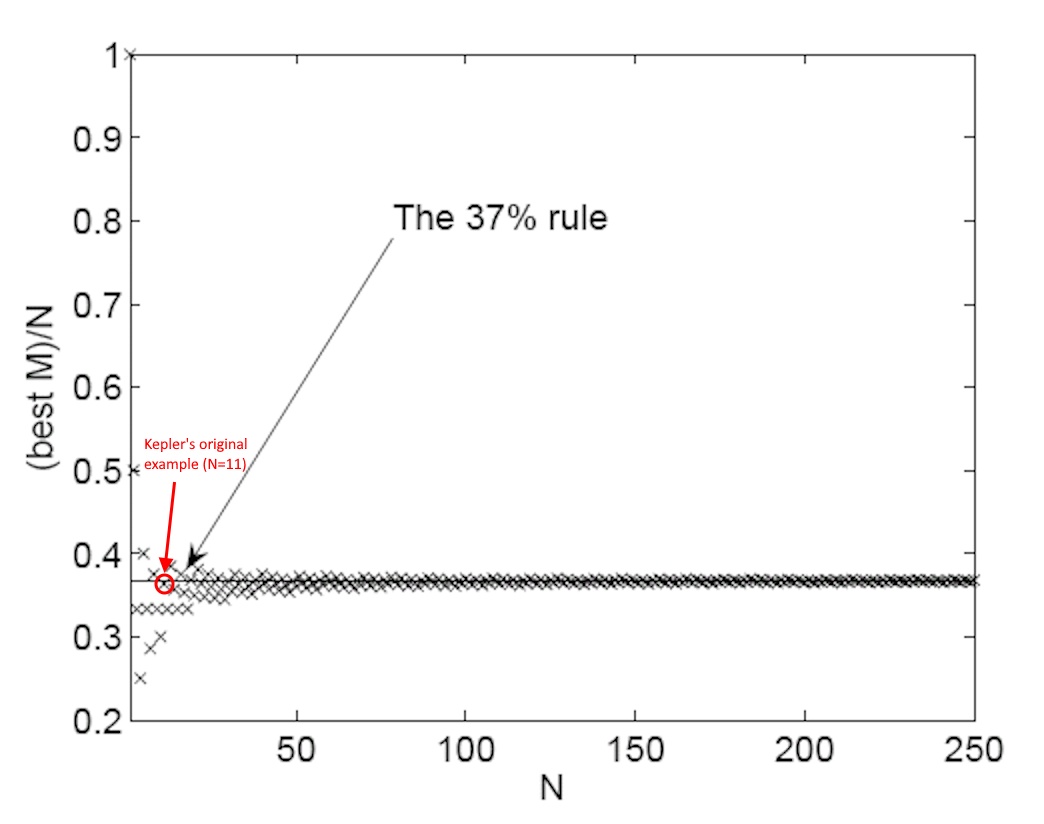
In mathematical circles, this puzzle has many names, and is perhaps best known as the secretary problem, rather than the marriage problem. However, it’s well-documented that the true origin of this problem goes all the way back to Johannes Kepler, who considered it in great detail from the years 1611-1613, after the death of his first wife. Kepler, while expected to remarry, wanted to ensure that he was making a sound choice. Over the ensuing two years, he not only spent time meticulously interviewing and researching 11 potential partners for himself, he worked out the probabilities — again, assuming a random distribution of what sort of “true happiness” he could arrive at with each of the potential candidates — of what sort of outcome he would arrive at dependent on which choice he made.
Assuming he’d encounter these 11 women sequentially, Kepler concluded that he should do his best to measure or estimate his happiness with each of his first four candidates, and irrespective of how he felt about them (even how he felt about them relative to his first wife), he should reject them all. Although there was a 4/11 (or about 36.36% chance) that one of those four would be his best match, there was a 7/11 chance (63.63%) that someone would be better than each of those four in the sample still to come. Out of those 7, so long as he picked the first one that he deemed “superior” to the first 4 options, he’d obtain the best chance of maximizing his happiness. It’s all the more remarkable, considering that natural logarithms were not even discovered until a little bit later: 1614.
The problem came up again and again in subsequent years, and has been applied to a variety of situations: hiring a job candidate, choosing a college, along with many variants where you could potentially return to previously rejected options. One notable variant is known as the “postdoc problem,” where your goal is not to pick the best candidate, but rather the second-best candidate, as the assumption is that “the best candidate will go to Harvard, so if you pick them, you’ll lose out.” (In that instance, it turns out that even with an optimal strategy, your probability of choosing your desired option is at best 1/4, rather than 1/e, demonstrating that it’s easier to pick “the best” option rather than “the second best” option.)
This general class of problem, mathematically, is known as an optimal stopping problem, where you have to take a decisive action after having gathered some sampling experience, with the goal of maximizing your payoff. Although there are many more complexities to all incarnations of this problem in reality, whether it’s making a big-ticket purchase, embarking on a romantic endeavor, or choosing a direction for your career, the notion of “sampling” first, followed by taking decisive action at an opportune time, is a universal aspect in achieving the maximum possible payoff.
Although no strategy can guarantee you’ll make the optimal decision, the way to maximize your probability of choosing the best is on firm mathematical footing. More than 400 years after Kepler, it’s still relevant to apply his lessons learned in probability to all of the biggest decisions in our lives.