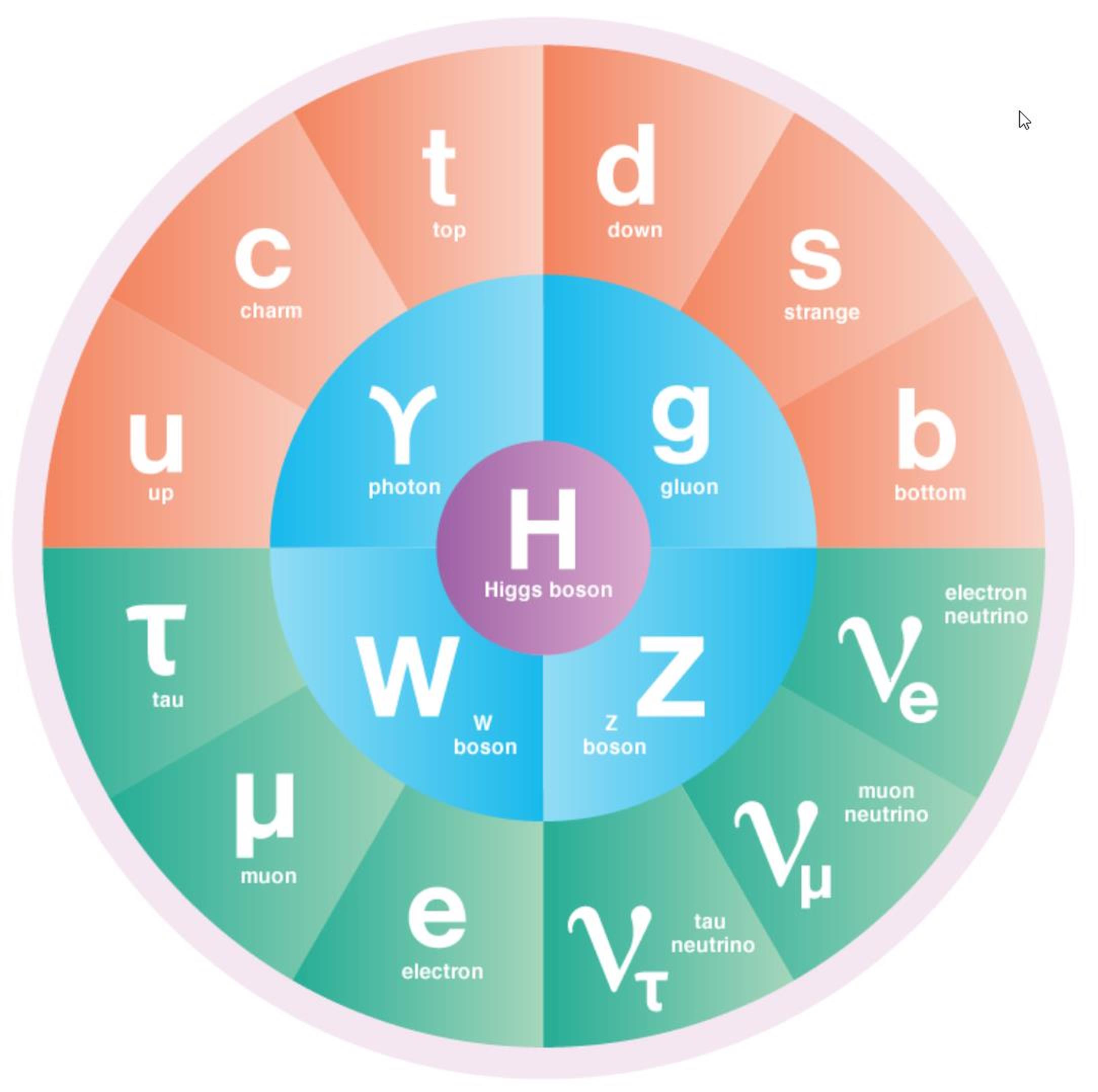
Ask Ethan: How do symmetries lead to conservation laws?
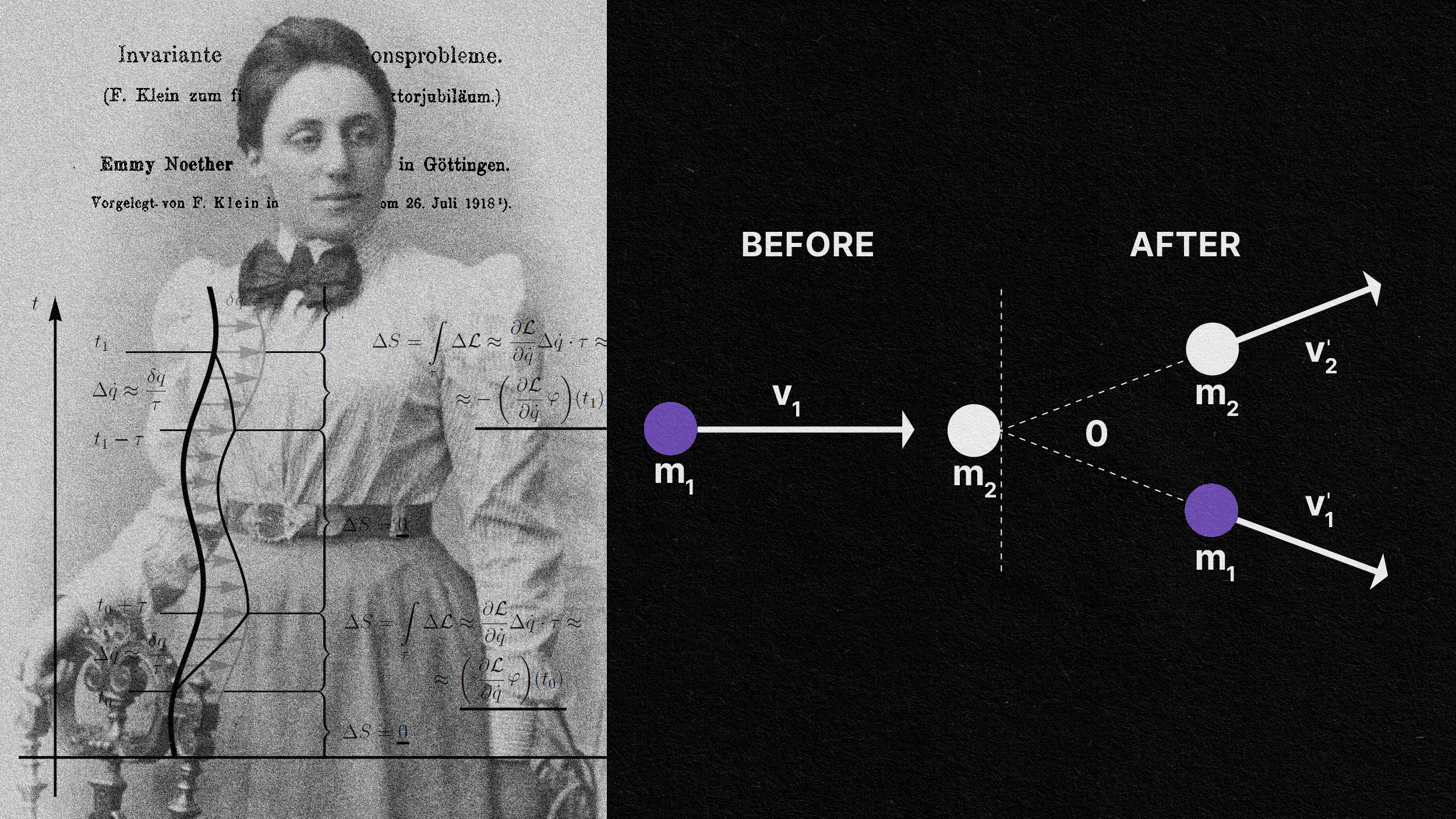
- First proven by Emmy Noether, there’s a profound connection between the symmetries in your theory and the conserved quantities that arise as a necessary consequence.
- There are both continuous and discrete symmetries, such as rotation or translation for the former and charge conjugation or reflection for the latter, but both types lead to conservation laws.
- However, where those symmetries are not obeyed, such as in the expanding Universe, those conservation laws can be violated. Here’s the profound story.
In this Universe, there are certain physical quantities that are — quite importantly — always conserved. Laws like the “conservation of energy,” “conservation of momentum,” and “conservation of angular momentum” are cornerstones of theories ranging from Newtonian mechanics all the way to quantum electrodynamics and beyond, and apply equally to planets in the Solar System as they do to collisions taking place inside the world’s most powerful particle accelerators. But these aren’t just empirical laws that we observe to be true; they’re an inevitable consequence of certain symmetries that these theories exhibit: an unavoidable connection required by Noether’s Theorem.
What’s the connection? That’s the topic of this week’s question from Kaleberg, who enjoyed this prior article on symmetries in physics and inquired with this follow-up:
“Excellent. Now do an article on Noether’s Theorem and show how symmetry leads to conservation laws. Doesn’t spatial invariance imply conservation of momentum, and doesn’t time invariance imply conservation of energy?”
Beyond the fact that symmetries exist, there’s an incredible connection between symmetries and conserved quantities, and it’s one of the deepest physical insights to come out of all of physics history.

Back in 1918, something fascinating occurred in the world of mathematics. Just a few years after the publication of Einstein’s general relativity — which changed how we viewed gravitation, spacetime, and the behavior of the Universe itself — people were puzzling over a seemingly peculiar fact. In the general theory of relativity, energy conservation didn’t appear as a natural consequence that was “baked into” the fabric of spacetime itself, but rather only appeared as an identity. David Hilbert, one of the foremost mathematicians of the time, wondered how, then, it was possible to constrain anything, even energy, within general relativity itself?
On July 23, 1918, a young woman named Emmy Noether summarized the content of her two theorems (previously published in 1915) for presentation to the German Mathematical Society. She wasn’t allowed to present them herself (being both too young and of a disallowed gender), so the great mathematician Felix Klein (of Klein bottle fame) presented them for her. These proofs showed, for the first time, that if you have a:
- physical system,
- with conservative (equal-and-opposite) forces at play,
- whose “action” has a differentiable symmetry,
then each and every independent differentiable symmetry that it possesses will also lead to an associated conservation law, and a “conserved quantity” by further association.

In simple terms, it means that every time you have a physical symmetry to your physical system, then there’s something physical associated with your system that will be conserved. For example, if your system — whether at rest or in motion — is symmetric under rotations, irrespective of how it’s oriented, then it’s an absolute necessity that angular momentum is conserved. Although her theorems were originally only applicable to continuous and smooth symmetries over physical space, has since been generalized to uncover profound connections between symmetries of the Universe and conservation laws. Three other examples, besides the implications of rotational invariance (or symmetry) for the conservation of angular momentum, include:
- If your system is time-translation invariant, which means it’s identical now to how it was in the past or will be in the future, then it leads to the law of conservation of energy.
- If your system is space-translation invariant, which means it’s identical here to how it was back over there or will be ahead down the road, then it leads to the law of conservation of momentum.
- And if your system is invariant under boosts (i.e., velocity transformations), then it leads to the conservation of four-momentum: the center-of-mass theorem.
Noether’s very general theorem, as you might intuit, has profound implications.

Take the time-translation invariant aspect of a physical theory. Throughout the 16th, 17th, 18th, and 19th centuries, most of the rules of mechanics had been arrived at empirically: through trial and error. The concept of energy — foreign to Newton — including the notion that there was such a thing as potential and kinetic energy that could be interconverted as objects fell or rose after being released, was only notable because of how useful it was. There was no fundamental reason known that would necessarily imply that energy was conserved; it was only observed that if you accounted for all the different forms of energy properly, that there was no way to either create or destroy it, only to convert it from one form to another.
But under the rules of Noether’s theorem, the notion that a system would have time-translation invariance — that it was the same in the past as it is in the present and as it will be in the future — that particular symmetry comes along with an associated conservation law: the conservation of energy. If the laws of nature do not vary with time, but rather are the same at all epochs, then the conservation of energy emerges as an unavoidable consequence. Noether’s theorem essentially elevates what were once empirical (i.e., simply observed to be the case) laws to predictable, derivable necessities of having a certain symmetry and/or invariance to your theory.

The profundity of Noether’s theorem was greatly appreciated by a great many 20th century mathematicians and physicists, not just Hilbert and Klein. The noted group theorist, Feza Gürsey, had the following to say:
“Before Noether’s Theorem, the principle of conservation of energy was shrouded in mystery, leading to the obscure physical systems of Mach and Ostwald. Noether’s simple and profound mathematical formulation did much to demystify physics.”
In classical electromagnetism, there are not just the electric and magnetic fields, but also electric and magnetic potentials. It’s interesting that the fields contain too little information to fully describe the system on their own, but the potentials contain too much information; you have redundancies encoded within them. Because of those redundancies, you have the freedom to choose what’s known as a gauge, and you won’t lose any information about your system. So if you have an invariance — a gauge invariance, in this case — Noether’s theorem tells us there must be a conserved quantity associated with it. As first recognized by Hermann Weyl, that conserved quantity is electric charge.
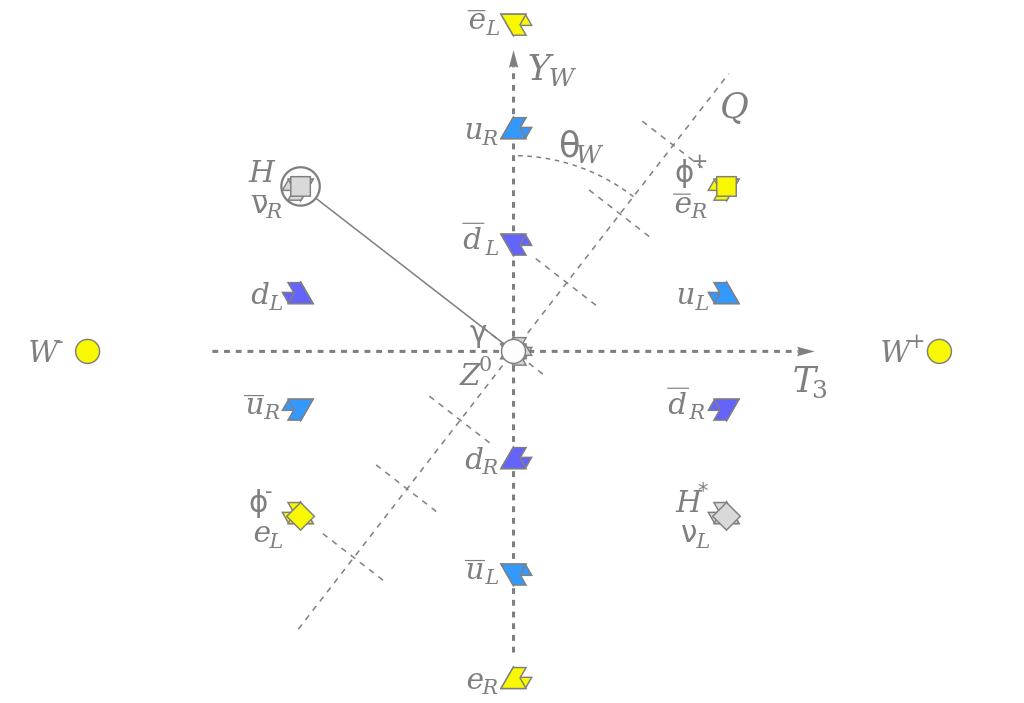
But the theorem goes even deeper than just saying, “If you have a symmetry or an invariance, then you have a conserved quantity.” It enables one to go a level deeper: if you know you must conserve a certain quantity for your theory to be valid, it tells you that your theory must preserve a certain associated symmetry or invariance in order to maintain that conserved quantity. Furthermore, it tells you that if your theory has an internal symmetry to it, that symmetry can generate interactions: the basis of Yang-Mills theory, as Yang and Mills devised a theory of the strong interactions between nuclear particles from the isospin symmetry they exhibited.
While Yang and Mills didn’t quite have the right idea in terms of specifics for how to formulate the interactions between nuclear particles, they can hardly be faulted for that. They were working only with protons and neutrons, not with the (more fundamental) idea of quarks composing those structures. Using very similar symmetry/interaction rules, the theory of quantum chromodynamics was developed to explain the strong interactions, whereas in electroweak theory, the electroweak interaction comes about from a (hidden) gauge symmetry that underlies the theory.

This powerful idea — of the connection between symmetries and invariances of a theory and the interactions and conserved quantities that arise — does have a couple of pitfalls that physicists should be wary of. The first is to beware of the temptation to impose additional symmetries or invariances in order to enable new interactions or to conserve quantities that may not, in fact, actually be conserved in nature.
For example, if you have spacetime and internal symmetries to the theories that pervade it, there’s a theorem known as the Coleman-Mandula theorem that ensures that all of the charges associated with your internal symmetries always remain unchanged regardless of how you transform them. This prevents you from taking a combination of spacetime symmetries and internal symmetries and “mixing” them in some complex way. For quarks, for example, there are flavor symmetries and spin symmetries, but they cannot mix together.
The Standard Model particles obey the rules of Lie algebras, but if you extend this to include Lie superalgebras, there becomes a new way to mix spacetime symmetries with internal symmetries: through supersymmetry. The temptation to make nature more symmetric is one we must beware of, as our Universe is fundamentally asymmetric in a number of important fashions.

It’s also true that some symmetries only apply under certain interactions or circumstances, meaning that violations of what we normally think of as conservation laws can sometimes be possible. Consider, for example, the three incredibly important discrete symmetries in particle physics:
- Charge conjugation (C): this symmetry involves replacing every particle in your system with its antimatter counterpart. It’s called charge conjugation because every charged particle has an opposite charge (such as electric or color charge) for its corresponding antiparticle.
- Parity (P): this symmetry involves replacing every particle, interaction, and decay with its mirror-image counterpart.
- Time-reversal symmetry (T): this symmetry mandates that the laws of physics affecting the interactions of particles behave the exact same ways whether you run the clock forward or backward in time.
The gravitational interaction, the electromagnetic interaction, and the strong nuclear interaction are all observed to obey each of these symmetries, individually as well as in combination with one another. The weak nuclear force, on the other hand, violates each of these symmetries individually (C, P, and T), as well as all combinations of any two of them (CP, PT, and CT). However, all three of them combined, CPT, are conserved under all interactions.

Going all the way back to the initial impetus of the puzzles of general relativity, it turns out that the invariance that leads to the conservation of energy — time-translation invariance — only persists in static spacetimes. The spacetime describing a non-rotating black hole, for example, is a static spacetime in which energy is conserved: it possesses time-translation invariance. But the spacetime describing the expanding Universe, the FLRW spacetime, either expands or contracts over time: an example of a non-static spacetime. In this case, which describes our actual Universe, the symmetry/invariance does not exist, and so the associated conserved quantity, energy, is not conserved in the expanding Universe.
An easy way to see this is to imagine that you have a photon — a quantum of light — that is emitted by one galaxy and heads toward another. If your spacetime is static and unchanging, the light simply travels from point A to point B, and neither its wavelength nor its frequency changes. Since the energy of a photon is defined by its wavelength, its energy remains the same: it’s conserved. But in the real Universe, the space between galaxies expands over time, including during the time that the photon journeys from point A to point B. As the light travels through this expanding space, its wavelength gets stretched to longer wavelengths, causing it to lose energy. That energy doesn’t “go” anywhere, nor does it need to; because we don’t have time-translation invariance, there’s no law of energy conservation in an expanding Universe.

For a long time — hundreds of years, in fact — it was assumed that all conservation laws were fundamental and without a greater cause: they would only be identified empirically, through phenomenological discovery. But thanks to the incredible and profound work of Emmy Noether, who proved the theorems that are now colloquially known as Noether’s theorem, we’re aware that there’s a powerful underlying relationship between all conservation laws and the symmetries and/or invariances that directly lead to them as a consequence. If a symmetry or invariance exists, an associated conserved quantity is inevitable.
Nevertheless, we must be careful. There is a great temptation to impose additional symmetries or hypothesize conservation laws that seem intuitively correct, but that may not reflect what actually exists within our Universe. Even the most vaunted of our conservation laws, the conservation of energy, is violated by the expanding Universe, and certain symmetries which are excellent under certain interactions may not be good symmetries with respect to others. Knowing the fundamental structure of your theory, and applying it correctly to the Universe, can teach you exactly what is and isn’t conserved in reality.
Send in your Ask Ethan questions to startswithabang at gmail dot com!