Ask Ethan: How do symmetries work in physics?

- Many of the laws of physics have symmetries, exhibiting the same behavior whether certain properties are conventional or "flipped," just as in the case of a mirror or folded piece of paper.
- During the 20th century, the recognition of certain symmetries in nature, including as respects particles and fields, led to many theoretical and experimental breakthroughs in fundamental physics.
- However, certain symmetries are either violated or broken by various processes, leading to a Universe that, thankfully, is asymmetric in fascinating ways. Here's how to make sense of it all.
In our everyday lives, as well as at the level of fundamental physics, symmetries play an important role. Human bodies have an approximate bilateral symmetry, or symmetry down the middle, and we judge more symmetric faces to be more visually appealing. Some animals, like starfish, have multiple lines of symmetry, as well as a rotational symmetry, where you can spin it by a certain angle (or set of angles) and it appears identical to the original. But in physics, there are extra kinds of symmetries that we don’t encounter conventionally: not just reflections, rotations, and translations, but discrete and continuous symmetries that are wholly divorced from our intuition and experience.
Can we break them down in ways that are understandable, even to a non-physicist? That’s the question of Shiloh Paul, who asks:
“I’m curious about the concept of ‘symmetries’ in physics. I still picture symmetry the grade school way – can you fold a piece of paper on top of itself? But when I try to understand symmetries in physics, which are apparently super fundamental, I struggle to even get the concept, much less all the mathematical support. Is there a “simple” way to understand what symmetries mean in terms of their importance to all of physics?”
There’s a lot to unpack and dive into, but let’s give it a try.

The familiar symmetries that you know, including:
- a folding symmetry (where you can find an “axis of symmetry” like the various letters shown above),
- a rotational symmetry (either continuously like a circle, or discretely like a starfish),
- or a translational symmetry (like moving either up-or-down an infinitely long line),
all apply to objects we encounter in the everyday world, and are examples of spatial symmetries. Physics absolutely has these symmetries as an integral part of it, and this ranges from objects with mirror symmetries, as shown below, to systems with objects in motion.
However, in physics, it isn’t just objects that have symmetries in physics, but also laws, equations, and entire theories. Kepler’s laws of planetary motion, for example, apply to planets regardless of which direction or orientation they orbit in: prograde or retrograde, in the ecliptic plane or out of the plane, and don’t depend on where, spatially, the object is in its orbit. Newton’s law of universal gravitation, Galileo’s equations of motion, and even Einstein’s theory of general relativity also obey all of these symmetries under the proper physical circumstances; these laws and rules are not different from place-to-place, for instance.

However, in physics, there are other types of symmetries that depend not only on space, but also on time. For example, consider what happens under the two following physical circumstances.
- You have a ball that bounces on a hard floor while moving to one side, and each time the ball bounces, a small amount of energy gets absorbed by the floor, causing the ball to come back up to a slightly lower height with each successive bounce.
- You have a ball in motion in the opposite direction to scenario number one, and as it bounces on the floor, a small amount of energy gets put into the ball with each successive bounce, causing the ball to rise to a slightly higher height with each successive bounce.
If the only thing you got to see was a recorded trajectory of the ball’s path, you would have no way of knowing which way the clock was running: forward or backward. Similarly, when you watch a satellite orbit around the Earth, because gravitation is a time-reversible theory, you have no way of knowing whether the satellite is in orbit with the clocks running forward or whether you’re watching the satellite in motion with the video being played backward. It isn’t just space that can be reversed or translated, but time as well, where an example of a time-translation invariant system is known as a time crystal.
There are other examples of discrete symmetries that don’t depend on space and time at all, however, and those are even harder to wrap your mind around. For example, if you’re talking to a particle physicist, there’s a symmetry between matter and antimatter particles, known as charge conjugation symmetry, or C symmetry. When you see the basketball bouncing, above, you have no way of knowing whether this is:
- a basketball made of matter, bouncing on a matter-based floor,
- or a basketball made of antimatter, bouncing on an antimatter-based floor,
because gravitation, the laws of motion, and the electromagnetic force are all symmetric under C symmetry: they’re equivalent whether you’re talking about matter or antimatter.
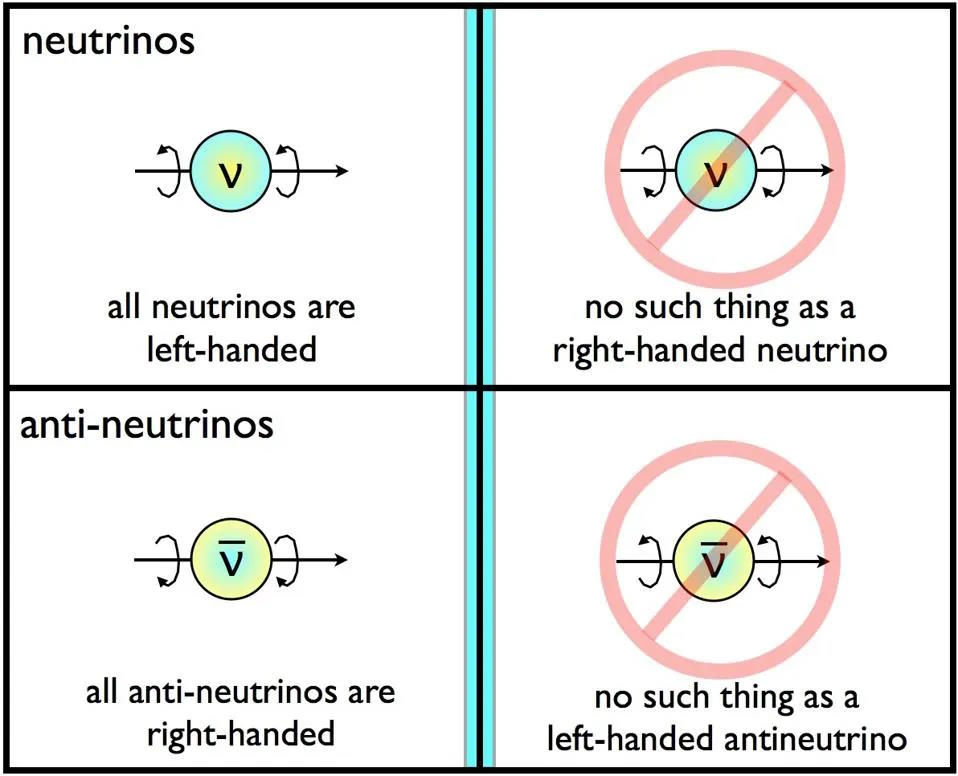
But just because you can envision a type of symmetry that could exist doesn’t necessarily mean that every force or interaction exhibits that symmetry. For example, the strong nuclear force, the electromagnetic force, and the gravitational force are all invariant under C symmetries, but the weak nuclear force is not. Consider a neutrino that moves in a particular direction: say, to the right. If you measure the spin of that neutrino, you’ll find that if you were to look “down” the direction it’s moving, it always spins clockwise. However, if you swap out that neutrino for an antineutrino, and had an antineutrino moving to the right, if you looked “down” the direction it was moving, it would always spin counterclockwise.
In general, when physicists talk about symmetries, they fall into a series of categories.
- Symmetries can be continuous or discrete, where there are an infinite number of discrete symmetries that you can apply to something that has a continuous symmetry. The letter O, for example, has discrete symmetries through any line that you draw through its center, but it has a continuous rotational symmetry if you rotate it about its center.
- Symmetries can also be preserved or violated, in the sense that you can imagine a Universe where everything obeys a specific symmetry, but that in our very real Universe, not everything actually does. Mirror image symmetry is a good example: if you only had the force of gravity to consider, a ball that was dropped or thrown would obey the same rules whether you watched its behavior in the mirror or in the real world. A neutrino, however, can only exist in the real world, because it’s left-handed; if you saw a neutrino’s image in a mirror, you’d know that it wasn’t a part of the real world, because it would appear right-handed, as illustrated above.
- And, in a more complicated sense, symmetries can be either restored, where it exists in a symmetric state, or symmetries can be broken, in the sense that you could have imagined it in a symmetric state, but the way you see it now, that symmetry has been violated.

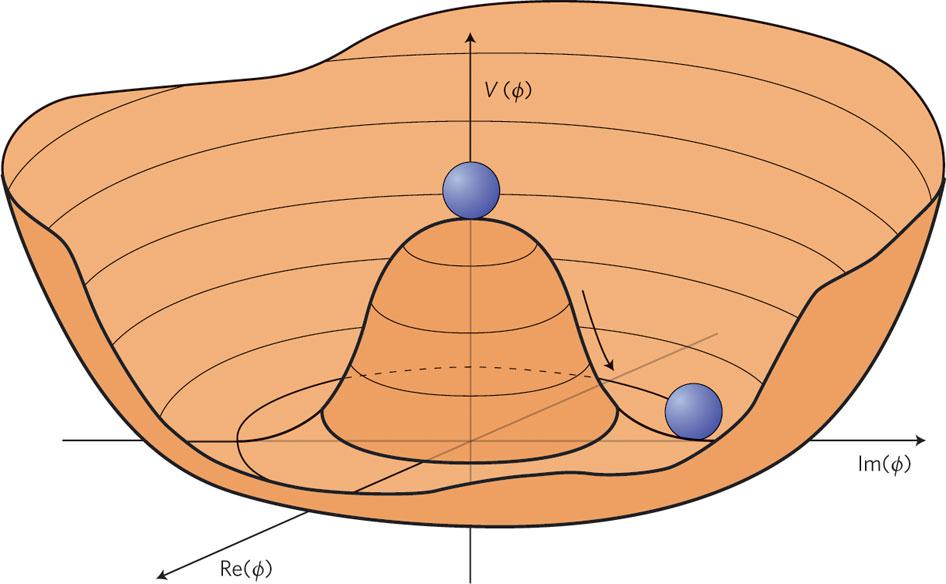
The sombrero-like potential that you see above, for instance, is a fantastic example of a potential that can exist in either a restored-symmetry state, as shown in yellow at the top, or in a broken-symmetry state, as shown in blue at the bottom. When the ball is at the top of this potential, all directions are equivalent. It doesn’t matter what direction the ball “faces,” all directions look like they’re “down,” into the valley below, with no discernible differences between any of the directions it can move.
Of course, that top-of-the-hill state isn’t exactly stable; it’s an example of what we call an unstable equilibrium in physics, where if there were any tiny perturbation, or “jitter” that we applied to it, it would roll down into the valley below.
And when it does that, corresponding to the blue ball down at the bottom, now that original symmetry is broken. If you look at the blue ball, all directions are no longer equivalent: you won’t have an equal likelihood of rolling “up” the hill to the peak, nor “up” farther away from the peak out of the valley. The only two directions that are equivalent are the abilities to roll either counterclockwise, which would take the blue ball around the valley in one direction, or clockwise, which would take the blue ball around the valley in the opposite direction. (If we further “tilted” the sombrero shape, so that there was one direction that was lower than the rest, that would take that last degree-of-freedom, or symmetric option, away from the blue ball, which is what happens in the theoretical case of the axion.)
Another way to look at things, though, is in terms of energy. The sombrero-like shape you see, above, you can also imagine as being the bottom of a wine bottle, but with “edges” that rise up far higher than the central peak in the middle of the bottom.
Imagine what would happen, now, if you filled the bottle with wine so thoroughly that the bottom “peak” in the middle of the bottle were completely covered over by wine. If you put a ball that floated, such as a ping-pong ball, in that bottle, it would float atop that wine, and all positions would be equivalent: it wouldn’t matter where the ball was, it would always be the same amount above the bottom of the wine bottle, at the same height. (In other words, it would have the same value along the y-axis, which corresponds to the value of energy that the field possesses.)
However, as you start draining the wine out of that bottle, the ball that’s floating atop the wine starts to drop. And things will remain in a symmetric state right until the level of the wine drops below the peak in the center of the bottle’s bottom. Once all locations are not equally likely for a ball to reside, and once all directions are not equally favored based on the ball’s position, that’s no longer a completely symmetric state, and so that’s the start of what we call a symmetry “breaking” in physics.

Sometimes, we deal with symmetries that are very badly broken in the modern Universe, but that were restored long ago at high energies: such as the electroweak symmetry, which triggers the Higgs mechanism when it breaks. In the symmetry-restored state, all of the bosons that made up the Standard Model would be massless: not just the gluons, but also four massless bosons, typically known as W1, W2, W3, and B. Just like the wine bottle example, at high energies (i.e., when the bottle is full enough), the state is entirely symmetric, and all values for the field are equivalent.
But as the bottle drains and energy in the Universe drops, that electroweak symmetry breaks, and that triggers the Higgs mechanism. All of a sudden, those four bosons now couple to the Higgs, and that gives three combinations of them mass: corresponding to the W+, W-, and Z bosons. However, one combination remains massless, and that corresponds to the massless photon, which still mediates the electromagnetic force. In addition, a new, single, massive boson, the Higgs boson, pops out of the theory. It’s only when the symmetry that triggers the Higgs mechanism breaks, the electroweak symmetry, that these particles gain a rest mass.
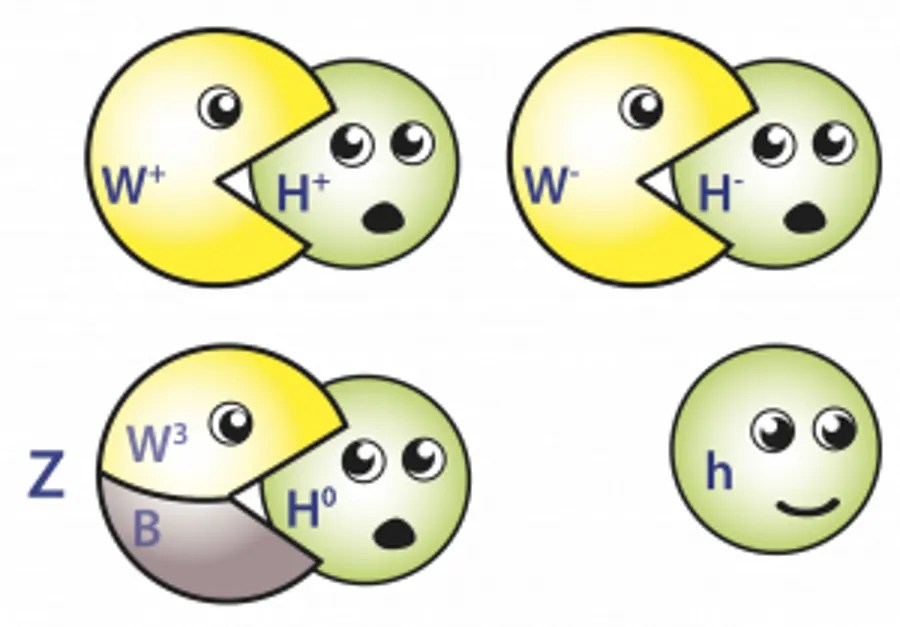
There are also approximate symmetries, where we know that things aren’t truly symmetric but treating them as though they are is informative and useful. For example, it’s sometimes useful to consider the lightest two (or even the lightest three) species of quarks, the up and down (and sometimes strange) quarks, as massless. If you consider that the bare mass/energy of the up quark is only about 2.3 MeV and the bare mass/energy of the down quark is only 4.8 MeV, then it doesn’t make sense that the proton (two up quarks and one down quark) and neutron (one up quark and two down quarks) should come in at 938 MeV and 939 MeV, respectively.
But if you treat those quarks as entirely massless and instead try to use chiral symmetry breaking to explain the mass generation for the quarks in the proton and neutron, you arrive at an idea of constituent quark masses, where the up and down quarks have constituent masses that are approximately equal, and are around ~313 MeV each. This can be extended to heavier quarks, but with less and less accuracy, as the strange, charm, bottom, and top quarks are all much heavier than the up-and-down quarks, with mass increasing substantially between each of those four heavier species. (Isospin, in nuclear physics, is another example of such an approximate symmetry.)

And finally, there are hypothesized symmetries, like supersymmetry, that would have astounding implications for our Universe if true. In our current understanding of physics, there are distinct categories that are most definitely not symmetric: fermions and bosons, for example, which are entirely different classes of particles from one another.
However, ideas like supersymmetry are ways of imposing additional symmetries on the Universe, and provide a framework for exploring what the consequences of adding such a symmetry would be. For example, supersymmetry’s big idea hypothesizes that for every fermion we have in the Standard Model, there’s a superpartner for it that’s a boson: a sfermion, with integer spin instead of half-integer spin. Similarly, for every boson we have in the Standard Model, there’s a superpartner for it that’s a fermion: a bosino, with half-integer spin instead of integer spin.
There are reasons to find a scenario like this theoretically attractive:
- it can explain the hierarchy problem, or why the masses of the Standard Model particles are so small compared to the Planck mass, as the superpartner particles cancel the mass contributions from the normal particles,
- it comes along with a possible dark matter candidate in the form of the lightest supersymmetric particle,
- and it could provide a pathway to the unification of the three Standard Model forces through the modified running of the coupling constants.
Of course, there is no evidence from experiment or observation in favor of supersymmetry; there’s clearly a limit to how symmetric nature actually is.

So, in summary, each symmetry that you can consider in physics can either be:
- discrete or continuous,
- exact or approximate,
- preserved or violated,
- restored or broken,
- and hypothetical or real,
and can be any or all of those things in combination. For instance, the symmetries of C (charge conjugation, or replacing particles with antiparticles), P (parity, or reflecting your system in a mirror), and T (time-reversal symmetry, or running the clock backward instead of forward) are each individually violated for the weak interactions. However, the combination of CPT together, where you do all of them at once, is conserved for all the interactions of the Standard Model, including the weak interaction individually.
However, it’s important to note that it’s the asymmetries in our Universe, and in our fundamental laws, that make our existence possible. If we extrapolated the ingredients of our Universe back to the earliest stages of the hot Big Bang, where many now-broken symmetries were restored, we would find that there would be no molecules, no atoms, no atomic nuclei, and no protons or neutrons at all. It’s only at our low-energy, highly asymmetric Universe that life, including human beings, is at all possible. Symmetry is incredibly important for fundamental physics, but the fact that the Universe is not symmetric is the most important fact of all when it comes to our existence.
Send in your Ask Ethan questions to startswithabang at gmail dot com!