No, the laws of physics are not time-symmetric

No matter when, where, or what you are in the Universe, you experience time in only one direction: forward. In our everyday experiences, clocks never run backward; scrambled eggs never uncook and unscramble themselves; shattered glass never spontaneously reassembles itself. But if you were to look at the laws of physics that govern the way the Universe works ⁠ — from Newton’s laws of motion down to the quantum physics of subatomic particles ⁠ — you’d find something peculiar and unexpected: the rules are exactly the same whether time runs forward or backward.

This corresponds to a certain symmetry of nature: T-symmetry, or time-reversal invariance. Our everyday experience indicates to us, quite strongly, that the laws of physics must violate this symmetry, but for decades, we couldn’t demonstrate it. From Newtonian physics to Maxwell’s electromagnetism to the strong nuclear force, every individual interaction ever observed appears to obey this time-reversal symmetry. It was only in 2012 that we finally experimentally showed that the laws of physics are different depending on which direction time runs. Here’s how we figured it out.

A wine glass, when vibrated at the right frequency, will shatter. This is a process that dramatically increases the entropy of the system, and is thermodynamically favorable. The reverse process, of shards of glass reassembling themselves into a whole, uncracked glass, is so unlikely that it never occurs spontaneously in practice. However, if the motion of the individual shards, as they fly apart, were exactly reversed, they would indeed fly back together and, at least for an instant, successfully reassemble the wine glass. Time reversal symmetry is exact in Newtonian physics.

Imagine you and a friend decide to go to Pisa, with one of you standing atop the famous leaning tower and the other located down at the bottom. From the top, whoever throws a ball off the edge can easily predict where it will land down on the bottom. Yet if the person at the bottom were to throw the ball upward with an equal-and-opposite velocity to the ball that just landed, it would arrive exactly at the location where the person at the top threw their ball from.

This is a situation where time-reversal invariance holds: where the T-symmetry is unbroken. Time reversal can be thought of the same way as motion reversal: if the rules are the same whether you run the clock forward or backward, there’s true T-symmetry. But if the rules are different when the clock runs backward from when the clock runs forward, that T-symmetry must be broken. And there are at least two very good, very fundamental reasons to think that this symmetry cannot hold in all instances.

Changing particles for antiparticles and reflecting them in a mirror simultaneously represents CP symmetry. If the anti-mirror decays are different from the normal decays, CP is violated. Time reversal symmetry, known as T, must also be violated if CP is violated. Nobody knows why CP violation, which is fully allowed to occur in both the strong and weak interactions in the Standard Model, only appears experimentally in the weak interactions.

The first is a proven theorem in physics known as the CPT theorem. If you have a quantum field theory that obeys the rules of relativity ⁠ — i.e., is Lorentz invariant ⁠ — that theory must exhibit CPT-symmetry. What we call C, P, and T symmetries are three symmetries that are both discrete and fundamental in the context of the Standard Model of particle physics:

• C-symmetry, which demands that you replace all particles with their antiparticles,
• P-symmetry, which demands that you replace all particles with their mirror-image reflections, and
• T-symmetry, which demands that you run the laws of physics backward in time instead of forward.

The CPT theorem tells us that the combination of all three symmetries, C and P and T all together, must always be preserved. In other words, a spinning particle moving forward in time must obey the same rules as its antiparticle spinning in the opposite direction moving backward in time. If C-symmetry is violated, then PT-symmetry must also be violated by an equal amount to keep the combination of CPT conserved. Since the violation of CP-symmetry had already been demonstrated long ago (dating back to 1964), we knew that T-symmetry had to be violated as well.

If you create new particles (such as the X and Y here) with antiparticle counterparts, they must conserve CPT, but not necessarily C, P, T, or CP by themselves. If CP is violated, the decay pathways — or the percentage of particles decaying one way versus another — can be different for particles compared to antiparticles, resulting in a net production of matter over antimatter if the conditions are right.

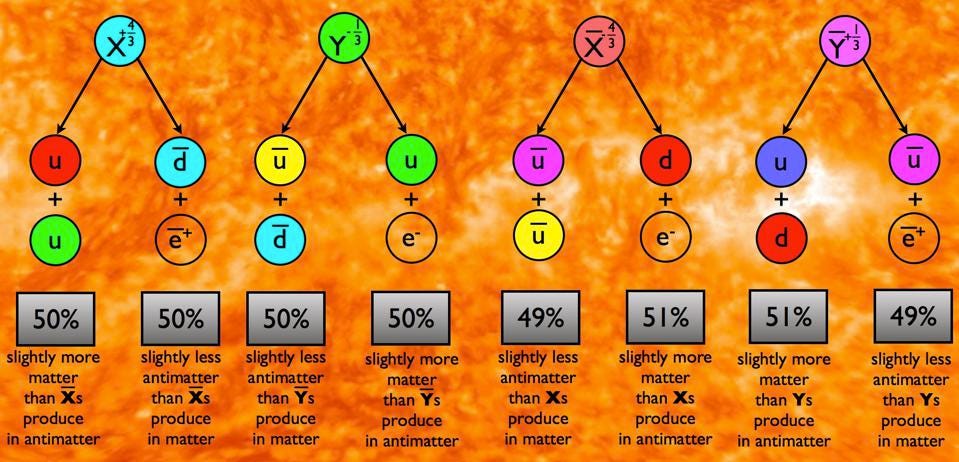
The second reason is that we live in a Universe where there’s more matter than antimatter, but the known laws of physics are completely symmetric between matter and antimatter.

It’s true that there must necessarily be additional physics to what we’ve observed to explain this asymmetry, but there are significant restrictions on the types of new physics that can cause it. They were elucidated by Andrei Sakharov in 1967, who noted:

1. The Universe must be in an out-of-equilibrium state.
2. Both C-symmetry and CP-symmetry must be violated.
3. And baryon number-violating interactions must occur.

Even if we hadn’t observed CP-violating interactions directly, we’d still have known that they must occur in order to create a Universe that’s consistent with what we observe: a Universe that isn’t matter-antimatter symmetric. And therefore, since T-violation is necessarily implied if you have the required CP-violation (in order to conserve the combination of CPT), time-reversal symmetry, or T-symmetry, cannot hold true under all circumstances.

In the Standard Model, the neutron’s electric dipole moment is predicted to be a factor of ten billion larger than our observational limits show. The only explanation is that somehow, something beyond the Standard Model is protecting this CP symmetry in the strong interactions. If the C symmetry is violated, so is PT; if P is violated, so is CT; if T is violated, so is CP.

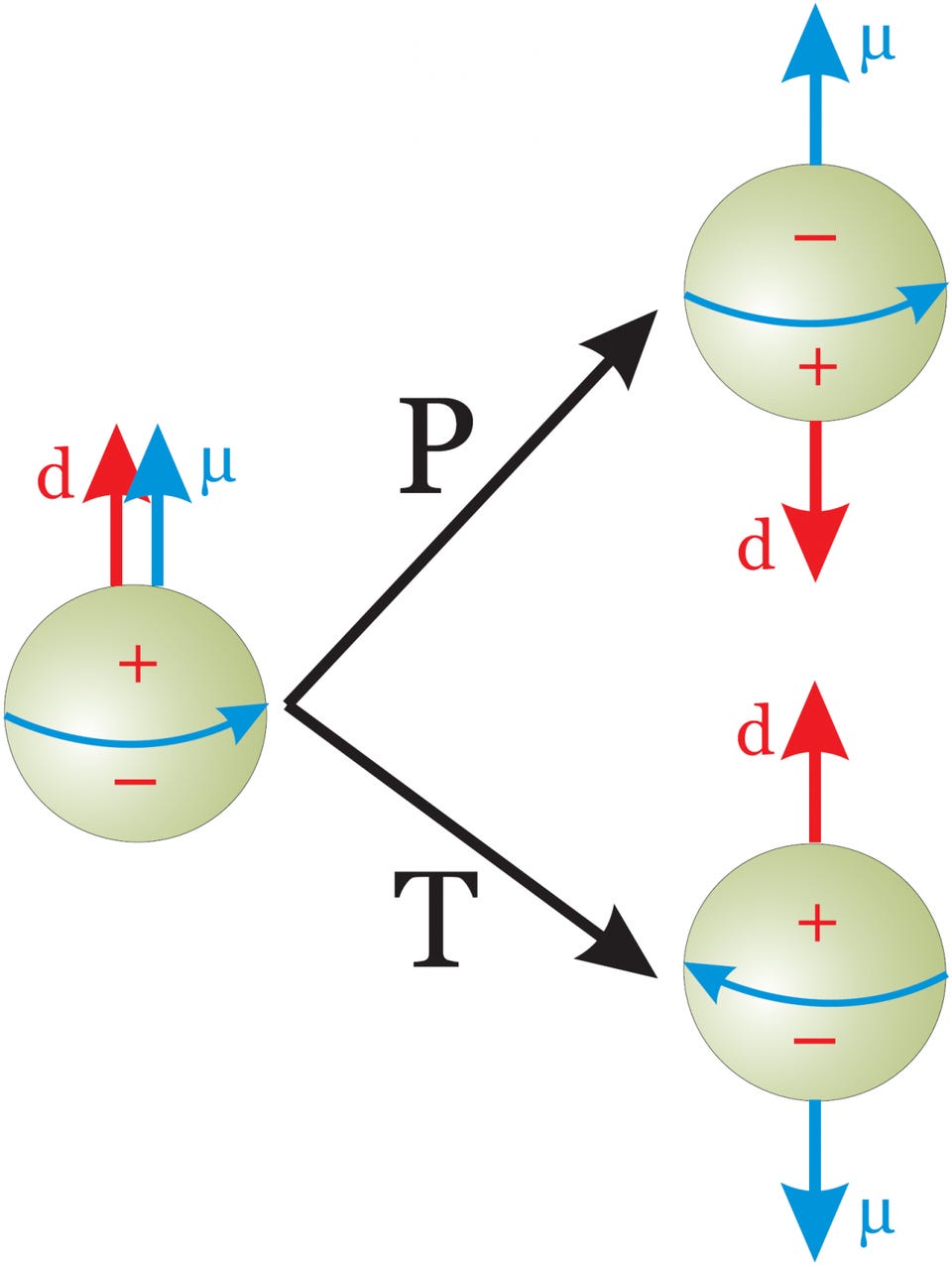
But there’s an enormous difference, in any science, between either theoretical or indirect evidence for a phenomenon and a direct observation or measurement of the desired effect. Even in instances where you know what the outcome must be, experimental verification must be demanded, or we run the risk of fooling ourselves.

This is true in any area of physics. Sure, we knew by watching the timing of binary pulsars that their orbits were decaying, but only with the direct detection of gravitational waves could we be certain that’s how the energy was being carried away. We knew that event horizons must exist around black holes, but only by directly imaging them did we confirm this prediction of theoretical physics. And we knew that the Higgs boson must exist to make the Standard Model consistent, but only by discovering its unambiguous signatures at the LHC were we able to confirm it.

So that set up the key task for physicists: rather than measuring other types of violations (like C, P, or CP) and using those violations in combination with what must be conserved (CPT) to conclude that the conjugate symmetry (e.g., PT, CT, and T, respectively) must also be violated, we’d need to explicitly and directly find a way to put T-symmetry to the test in an instance where it should be violated.

The first robust, 5-sigma detection of the Higgs boson was announced a few years ago by both the CMS and ATLAS collaborations. But the Higgs boson doesn’t make a single ‘spike’ in the data, but rather a spread-out bump, due to its inherent uncertainty in mass. Its mass of 125 GeV/c² is a puzzle for theoretical physics, but experimentalists need not worry: it exists, we can create it, and now we can measure and study its properties as well. Direct detection was absolutely necessary in order for us to be able to definitively say that.

This would require a lot of thought, and a very clever experimental setup. What one must do is design an experiment where the laws of physics could be directly tested for differences between an experiment that runs forward in time versus one that runs backward. And since — in the real world — time only runs forward, this requires some truly creative thinking.

The way to think about this is to remember how entangled quantum states work. If you have two quantum particles that are entangled with one another, you know something about their combined properties, but their individual properties are indeterminate until you make a measurement. Measuring the quantum state of one particle will give you some information about the other one, and will give it to you instantaneously, but you cannot know anything about either individual particle until that critical measurement takes place.

Typically, when we think about quantum entanglement of two particles, we perform experiments involving stable particles, like photons or electrons. But there’s only one type of physics process where CP-violation is known to occur: through decays that proceed through the weak nuclear interaction.

When the neutral kaon decays, it typically results in the production of either two or three pions. Supercomputer simulations are required to understand whether the level of CP-violation, first observed in these decays, agrees or disagrees with the Standard Model’s predictions. With the exception of only a few particles and particle combinations, almost every set of particles in the Universe are unstable, and if they don’t annihilate away, they will decay in short order.

In fact, this direct type of CP-violation was observed in 1999, and by the CPT theorem, T-violation must occur. Therefore, if we want to test for direct violation of time reversal symmetry, we’d have to create particles where T-violation occurs, which means creating either baryons or mesons (unstable composite particles) that decay via the weak interactions. These two properties, of quantum indeterminism and of unstable particles that decay through the weak interactions, were what we needed to leverage in order to design the exact type of experiment required to test for the direct violation of T-symmetry.

The way to go about testing time reversal violation directly was first proposed only quite recently, as the technology to produce large numbers of particles that contain bottom (b) quarks has only come about in the past few years. The ϒ particle (the Greek letter upsilon) is the classic example of a particle containing bottom quarks, as it’s actually a meson made of a bottom quark and a bottom antiquark pair.

Like most composite particles, there are many different energy states and configurations it can exist in, similar to how the hydrogen atom exhibits a variety of possible energy states for the electron to be in. In particular, it was suggested that the 4s energy state — the third excited spherically symmetric energy level — holds some special properties, and might be the best candidate for observing T-symmetry violation directly.

In an atomic system, each s orbital (red), each of the p orbitals (yellow), the d orbitals (blue) and the f orbitals (green) can contain only two electrons apiece: one spin up and one spin down in each one. In a nuclear system, even in a meson which has just a quark and antiquark, similar orbitals (and energy states) exist. In particular, the 4s state of the Upsilon (ϒ) particle has particularly interesting properties, and was created hundreds of millions of times for the BaBar collaboration at SLAC.

Why would this be the case?

Because the ϒ(4s) particle, when you create one, decays into into both a neutral B-meson (with a down quark and an anti-bottom quark) and a neutral anti-B-meson (with a bottom quark and an anti-down quark) about 48% of the time. At an electron-positron collider, you have the freedom to tune your collisions to occur at the exact energy needed to create a ϒ(4s) particle, meaning that you can create enormous numbers of B-mesons and anti-B-mesons for all your particle physics needs.

Each of these mesons, either a B-meson or an anti-B-meson, can decay in a few possible ways. Either you can produce:

• a J/ψ (charm-anticharm) particle and a long-lived Kaon,
• a J/ψ particle and a short-lived Kaon,
• or a charged lepton and a variety of other particles.

This is interesting, because the first decay has a known value for its CP, the second has a known value for its CP that’s opposite to the first, and the third decay identifies whether it’s a B-meson or anti-B-meson by virtue of the sign of the charge on the lepton. (A positively-charged anti-lepton indicates a B-meson decay; a negatively-charged lepton indicates an anti-B-meson decay.)

A setup of the system used by the BaBar collaboration to probe time-reversal symmetry violation directly. The ϒ(4s) particle was created, it decays into two mesons (which can be a B/anti-B combination), and then both of those B and anti-B mesons will decay. If the laws of physics are not time-reversal invariant, the different decays in a specific order will exhibit different properties. This was confirmed in 2012.

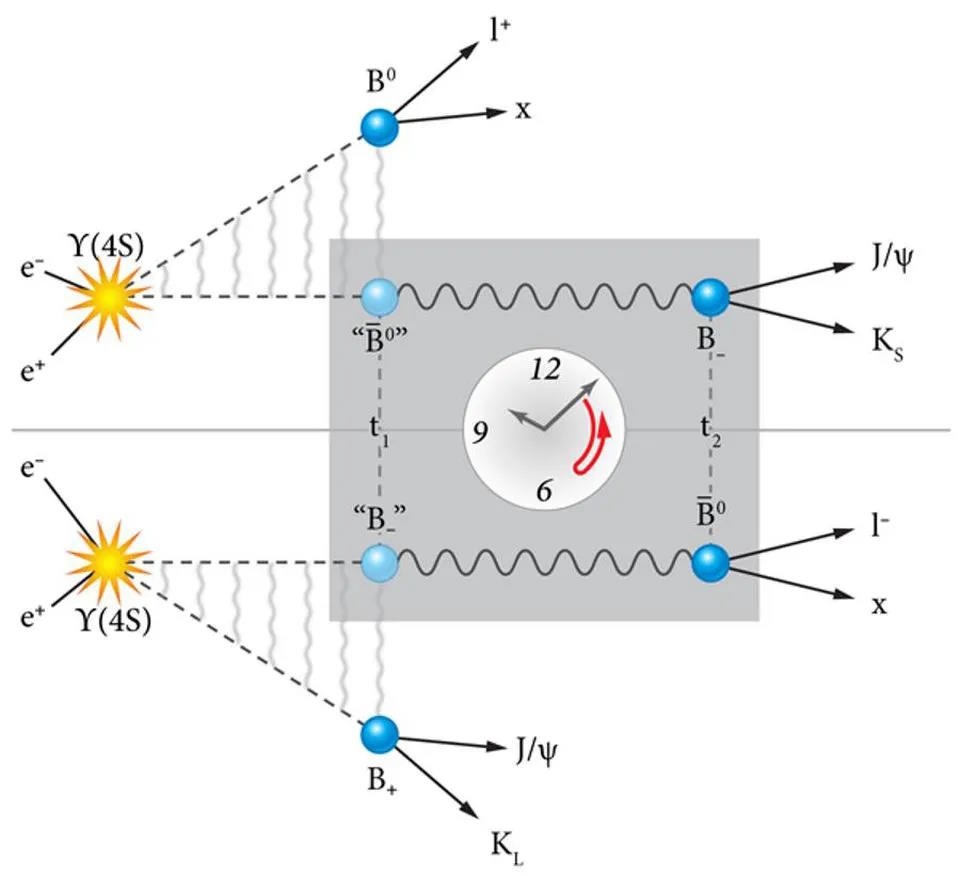
Knowing that information lets us set up a method for detecting T-symmetry violation. Whenever one member of the B/anti-B pair of mesons decays into a J/ψ and a Kaon while the other member decays into a lepton (plus other particles), this gives us the opportunity to test for time-reversal violation. Because these two particles, the B-meson and the anti-B-meson, are both unstable, their decay times are only known in terms of their half-lives: decays don’t occur all at once, but at random times with a known probability.

Then, you’ll want to make the following measurements:

1. If the first meson to decay does so into a positively charged lepton, you know that the second must be an anti-B particle.
2. You then measure the decay of the anti-B particle, and see how many of them give you a decay into a short-lived Kaon.
3. Then, you look for events where the order of decays is reversed and the initial and final states are exchanged, i.e., where the first meson decays into a long-lived Kaon and is followed by the second one decaying into a negatively-charged lepton.

This is a direct test of time-reversal violation. If the two event rates are unequal, the T-symmetry is broken. After the creation of over 400 million ϒ(4s) particles, time-reversal violation was detected directly: a feat accomplished by the BaBar collaboration back in 2012.

There are four independent time-reversal-violating asymmetries in the decaying ϒ(4s) system, corresponding to decays into charged leptons and charm quark-antiquark combinations. The dashed blue curve represents the best fit to the BaBar data without T-violation; you can see how absurdly bad it is. The red curve represents the best-fit data with T-violation. Based on this experiment, direct T-violation is supported at the 14-sigma level.

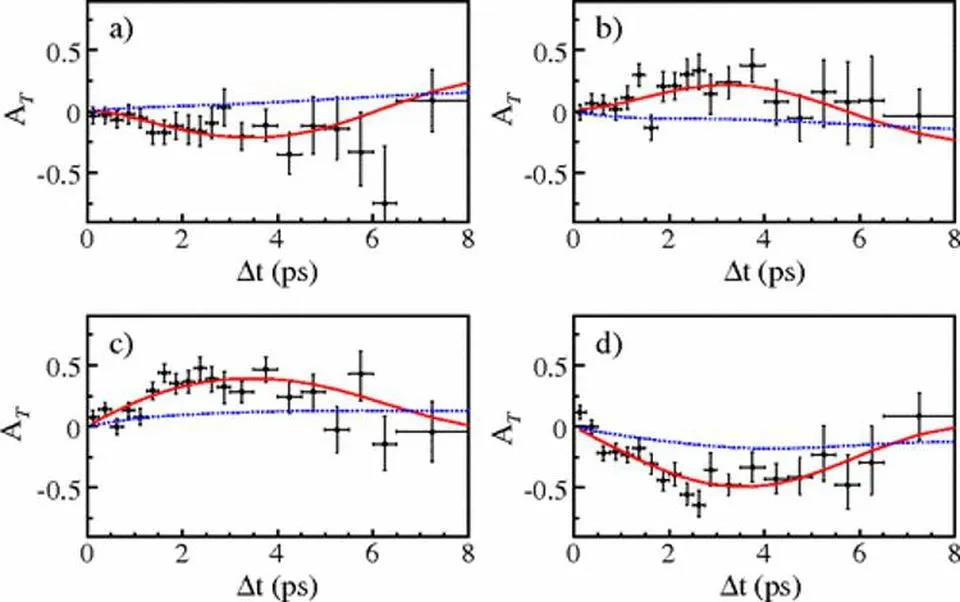
The test for whether you can reverse the initial and final entangled states in the 4s-excited state of the ϒ-meson is, to date, the only test ever performed to see if T-symmetry is conserved or violated in a direct fashion. Just as anticipated, the weak interactions really do violate this T-symmetry, proving that the laws of physics are not perfectly identical dependent on whether time is running forward or backward.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

In particle physics, the gold standard for experimental significance is a threshold of 5-sigma. Yet BaBar physicists achieved a statistical significance of this result at a 14-sigma level: a remarkable accomplishment.

So why, then, is this groundbreaking result something you’ve likely never heard about before?

Because at right around the same time, in the same year, in the world of particle physics, the results of the BaBar collaboration were overshadowed by slightly bigger particle physics news occurring at nearly the same time: the discovery of the Higgs boson at the Large Hadron Collider. But this result, demonstrating that the laws of physics are not time-symmetric, might be Nobel-worthy as well. The laws of nature are not the same forward and backward in time. Eleven years after it was established, it’s time the world truly knew about the magnitude of this discovery.