Ask Ethan: What’s the real science behind Google’s time crystal?

- Google’s quantum computing team, in a first, has developed and demonstrated a discrete time crystal on a quantum computer.
- By driving the system with a microwave pulse, they can get it to return to its original quantum state periodically, with no thermal noise or decoherence effects.
- However, claims that it violates thermodynamics, is otherworldly, or changes physics forever are all demonstrably untrue and misrepresentative of the actual quality research.
It is tempting, whenever a new discovery comes along, to imagine a whole slew of revolutions that might soon ensue. After all, anytime you can suddenly do or accomplish any task that was previously impractical or even (thought to be) impossible, that is one less obstacle standing in the way of even your loftiest, pie-in-the-sky dreams. However, no matter what discoveries ensue, the fundamental laws of physics that underlie reality must always be obeyed; you might be able to cajole nature into doing a lot of clever things, but you cannot very well break the rules that govern it. If you could, we would have to write down new laws, because the old ones would no longer be valid. Despite all the tricks we have developed, we cannot create fundamental magnetic monopoles, violate the conservation of momentum or energy, or work our way around the second law of thermodynamics.
Yet a recent article, touting a brand new discovery involving time crystals and Google’s quantum computer, claims to do just that: evade the second law of thermodynamics. Is that even right? Patreon supporter Chad Marler wants to know, asking:
Hi Ethan… I was reading some headlines and came across this article. While I suspect the innovation was real, some of the wording in the article made my [nonsense] detector go off… it sounds like something you would hear on an Art Bell show.
I will tell you, up front, that the scientific paper is legit, but the recent article is full of misconceptions and misinterpretations. Let’s dive in and find out what it is all about.
What is a time crystal?
Unlike most things in physics, where theorists imagine a possibility far out of reach of current or near-future technology, time crystals have only been around for a very short time, even in our minds. In 2012, Nobel Laureate Frank Wilczek proposed that a new state of matter might exist: a time crystal. Most of us know what a normal crystal is: a repeating, rigid lattice or grid of particles, like atoms or molecules, that compose a solid, ordered structure.
When we talk about time crystals, however, there is no lattice, no grid, and no solid, ordered structure. The important component of a time crystal, at least conceptually, is the “repeating” part. Whereas a conventional crystal has a structure that repeats in space, meaning it exhibits translational symmetry (if you move within the crystal, the structure looks the same everywhere), a time crystal should repeat its configuration, periodically, in time.
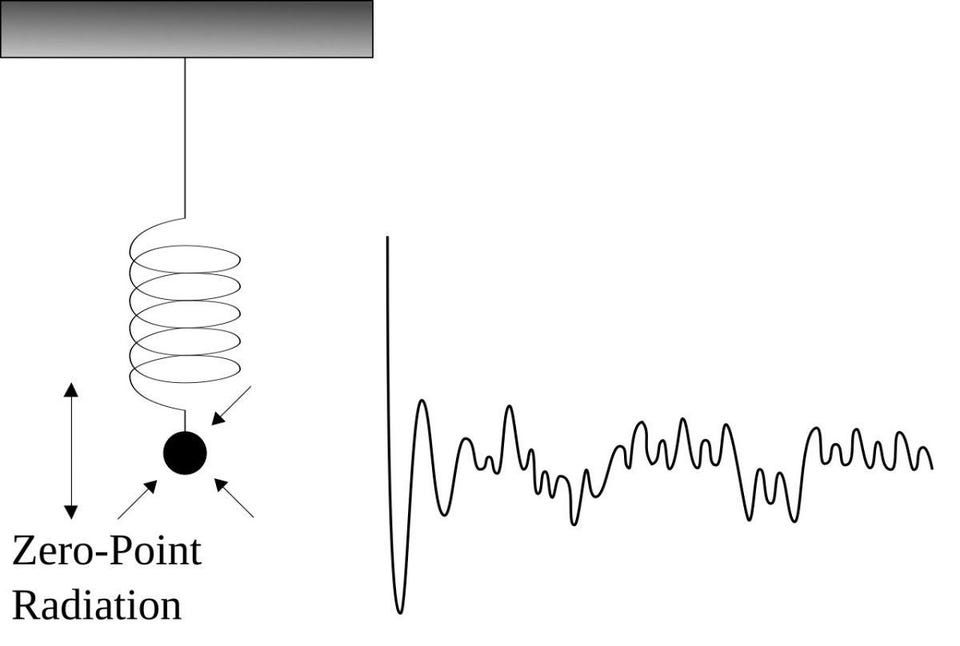
Originally, when time crystals were first considered, they were presumed to be impossible for a number of reasons. There were theorems published that proved their impossibility. There were assertions that a system that transitioned from lower-to-higher energy states would not return to its original state again spontaneously, and then go back-and-forth between those two states, because that would indicate some type of perpetual motion, violating the second law of thermodynamics and the conservation of energy.
But not only did theorists find loopholes in those theorems, but more impressively, experimentalists just went right ahead and created them in the lab. In 2016, Norman Yao and his team came up with a scheme to create a time crystal through a very clever plan. Instead of taking a closed, constant system, he proposed leveraging a system with out-of-equilibrium conditions. He would then “drive” that system externally, making it an open (rather than a closed) system and achieving the much sought after “time crystal” state.
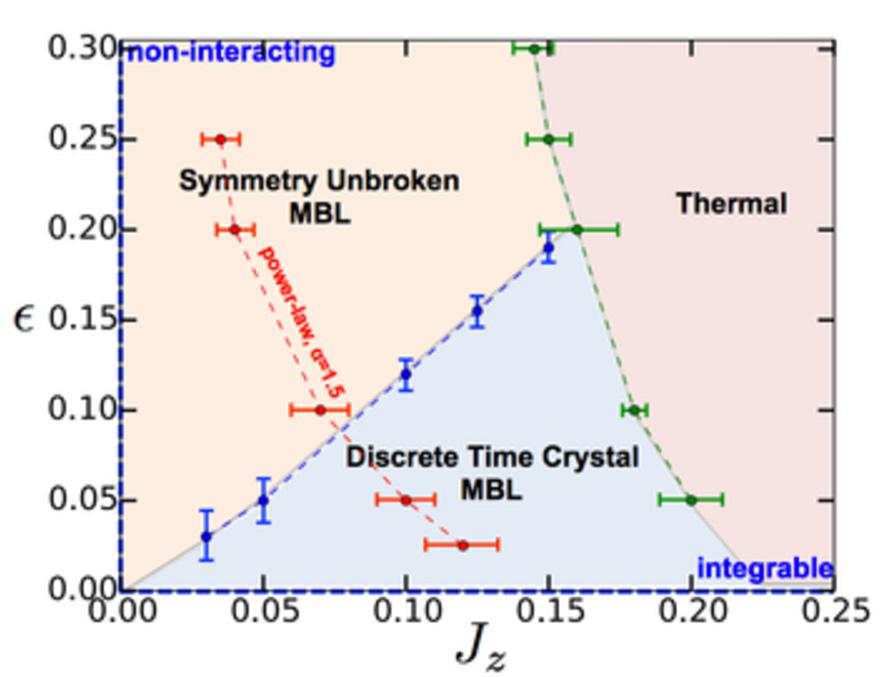
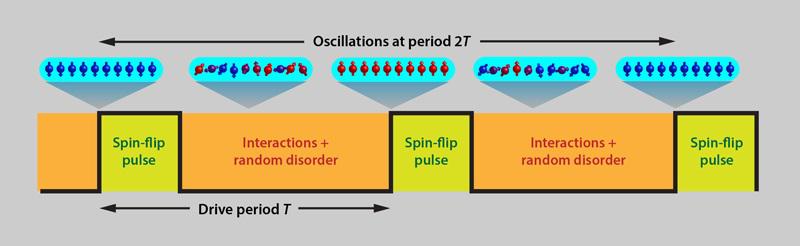
It is a little bit complicated, but you can imagine that you have a bunch of atoms that have a spin, and those spins have directions: dipole moments. The way you can “drive” the system is by subjecting the system to spin-echo pulses that contain imperfections, but which occur periodically while allowing interactions to randomly occur in the intermediate times. If you get the combinations of these dipole moments of the spins and the spin-echo pulses to behave in a certain fashion, you could get a time crystal.
The hard part, though, is avoiding what normally happens when you interact with a system: If there is an exchange of energy, that energy gets transferred throughout the system, internally, causing runaway heating due to many-body interactions. Somehow, you have to:
- drive the system, externally, with a spin-flip pulse,
- so that you get a periodic response,
- that is proportional to the time at which you pulse the system,
- and at some multiple of the period, you return to your initial state,
- while the “time crystal” only oscillates away from and then back into that initial state.
Only if you go back, periodically, to exactly your initial state, with no extra heating and achieve a pure steady-state can you make a time crystal.
How can you make one in real life?
Yao’s work first appeared in August 2016, and within mere months, two independent groups put it to the test:
- Mikhail Lukin‘s at Harvard University, and
- Christopher Monroe‘s at University of Maryland.
They tried to set up a system precisely as Yao had demanded but, because the conditions are so general, wound up taking vastly different approaches.
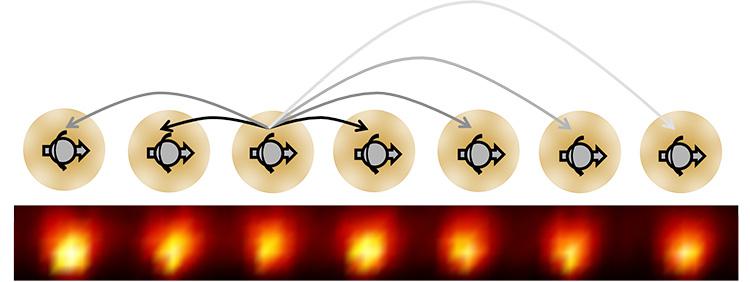
Monroe’s group took a series of yttrium atoms all lined up, in a one-dimensional line, all coupled together via their electrostatic interactions. When they subjected this atomic line to a series of spin-flip pulses, they found that the system would return to its initial state every two full pulse periods. Meanwhile, Lukin’s group took an actual diamond crystal that contained somewhere on the order of ~1,000,000 spin-impurities within it and pulsed those impurities within the crystal with microwave radiation. That radiation flipped their spins, but time crystal oscillations were only observed every three full pulse periods — whereupon the crystal would return to its initial quantum state.

This occurred for both groups, interestingly enough, even when the driving pulses were imperfect. You could:
- alter the magnitude of the pulse, making it stronger or weaker,
- vary the frequency of pulsation, making it a little quicker or slower,
- turn up or turn down the amount of noise and/or interactions that occurred between the pulses,
- or change the conditions of the environment that the system is placed in,
and still recover this time crystal behavior. Surprisingly, for these non-equilibrium systems, there is a lot of wiggle-room as far as what you can do and still observe this time crystal behavior.
But as they were originally envisioned by Wilczek in 2012, an idealized time crystal would occur in a system that was in thermal equilibrium — that was neither absorbing nor emitting energy from or to the surrounding environment. In order to create a time crystal, you needed to have an open system that could exchange energy with its external surroundings, and that system needed to be driven at a periodic frequency. Moreover, the imperfections in the driving could not be too large, or the crystal would “melt” in precisely the fashion we want to avoid: with runaway heating occurring from many-body interactions.
What did the Google team, using a quantum computer, actually do?
Back when these time crystals were first realized in 2016/2017, it was recognized that time crystals could conceivably be applied to quantum computers. Instead of encoding a bit, like the “0” or “1” a standard computer encodes, a quantum computer encodes a qubit, which is a probability-weighted superposition of both “0” and “1” simultaneously. Although you can only measure a “0” or “1” at the end, the fact that you have many qubits allows you to see whether you have preserved the quantum behavior of the system (or not), whether your results are error-free (or not), and what type of final-state distribution you get and whether it matches your theoretical predictions.
The hard “problem” with a quantum computer is the problem of decoherence: Over relatively short timescales, the system interacts with the surrounding particles, and this causes you to lose the quantum behavior you are trying to preserve. For Google’s quantum computer, which is based on superconducting qubits (as opposed to quantum dots or ion traps, for example), you get a coherence timescale of about 50 microseconds. You can only perform perhaps a few dozen computations before decoherence ruins your experiment, and you lose the quantum behavior you sought to maintain and measure. (Or, more precisely, before too many errors, including errors from simple crosstalk between qubits, simply transform your signal into noise.)
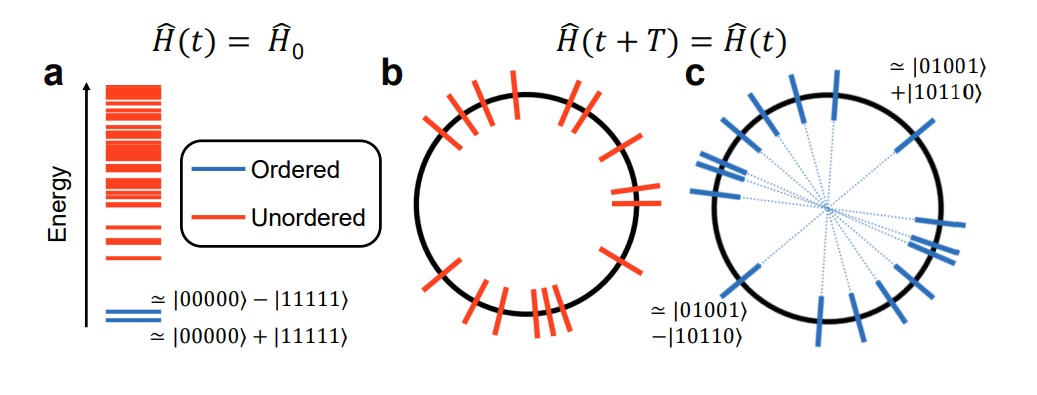
Instead of using a dynamical phase like the spins of atoms, though, a quantum computer allows you to use a different property: the order of eigenstates in many-body systems. If you brought your qubits into an equilibrium setting, you would see that there was order in the lowest energy states and unordered states at higher energies. That is why, under normal circumstances, if you allow too much energy to propagate through your system, you just wind up with featureless, unordered systems; it is like the heat or energy just randomized everything.
However, some systems can exhibit what is called MBL: many-body localization, where you get local conservation laws and only a discrete number of ordered states. When you drive the system, which the Google team did with pulsed microwaves that cause the qubits to flip, your qubits have the potential to behave just like the dynamical phases did when we were measuring atomic spins: If the qubits do not absorb heat or impart energy to their surroundings, they can simply flip between different ordered states. With enough pulses, you can conceivably recover your original state.
Sure enough, every two full periods of the microwave pulses resulted in a recovery of the original state: a time crystal. Not bound by these decoherence effects any longer, the researchers could maintain this time crystal state for up to ~100 seconds, a remarkable achievement.

And how do the claims in the LiveScience article hold up?
Although the article does a fine job of describing the experiments performed themselves, there is a howler of a statement made early on:
With the ability to forever cycle between two states without ever losing energy, time crystals dodge one of the most important laws of physics — the second law of thermodynamics, which states that the disorder, or entropy, of an isolated system must always increase. These bizarre time crystals remain stable, resisting any dissolution into randomness, despite existing in a constant state of flux.
There is no dodge; the second law of thermodynamics applies to closed systems, not open ones. The disorder of the system, if you include the microwave pulses and the external environment, does in fact go up, just as predicted. The crystals oscillate between allowable states and return to their original ones when driven properly, just as their non-qubit analogues did years prior. In order to do this, the researchers needed to discriminate between external decoherence and internal thermalization, both of which can destroy the quantum state they are seeking to maintain, which itself is an admirable achievement.

Although it may be fun to claim, as the headline of the article did, that this is “otherworldly” and “could change physics forever,” it is more like imagining you have got a skillet with different sized and shaped mollusks in it and a chef who jiggles the pan in a way that makes the shelled creatures flip. Some will flip 180°, others 360°, others 540°, etc. In the quantum world, some of these mollusks can take on in-between values, too. But after a certain number of jiggles, the mollusks all wind up the same way they started, regardless of what that specific initial configuration was. That is all the Google team is doing, but instead of mollusks or spinning atoms, they are using the eigenstates of a quantum computer.
Which, if we are being honest, is still a remarkable achievement! This is a new kind of time crystal, a new way of achieving it, and one with the potential to study non-equilibrium phases of matter on a quantum computer. And although you have to pump energy into the system in pulses, the time crystal can, in fact, return to whatever specific state it began with, even with small imperfections occurring in the “flips,” without destroying, decohering, or losing the nature of the quantum state due to thermal instabilities. No laws are violated and the physics we know is not changed in any way, but this is a phenomenal achievement nonetheless. In a mere nine years, we have gone from theorizing the existence of time crystals to creating them to observing them on a quantum processor. When a new field yields significant advances so quickly, it compels us to pay attention.
Send in your Ask Ethan questions to startswithabang at gmail dot com!