Strange but true: the expanding Universe doesn’t conserve energy

In all the Universe, one of the most fundamental rules of all is the law of energy conservation. In its simplest form, it states that energy can neither be created nor destroyed, but only transformed from one type into another. Regardless of transformations between different types of energy, including:

• gravitational potential energy,
• chemical energy,
• the energy of radiation,
• thermal (heat) energy,
• kinetic (motion) energy,
• rest mass energy,
• as well as any other form of energy you can dream up,

the total amounts of “initial” and “final” energy in any physical system must always add up to the same values.

But there’s an underlying reason for why energy is always conserved: it’s because there’s a physical symmetry that corresponds to the conserved quantity of energy. In this case, it’s time-translation invariance: the notion that physical properties and laws don’t evolve with time. But there is a very important physical property — not on Earth, but on cosmic scales — that actually does evolve with time: the distance between any two cosmic objects that aren’t gravitationally bound together. In the expanding Universe, distant galaxies recede from one another, growing farther apart with time.

Does that imply that energy is no longer conserved in an expanding Universe? Bizarrely, it actually does. As strange as it may seem, it’s actually true: energy is not conserved in the expanding Universe. Here’s the science behind why.

The gravitational behavior of the Earth around the Sun is not due to an invisible gravitational pull, but is better described by the Earth falling freely through curved space dominated by the Sun. The shortest distance between two points isn’t a straight line, but rather a geodesic: a curved line that’s defined by the gravitational deformation of spacetime. The notion of “distance” and “time” is unique for every observer, but under Einstein’s description, all frames of reference are equally valid, and the “spacetime interval” remains an invariant quantity.

Back in 1915, something fascinating occurred in the world of mathematics. No, I’m not talking about the publication of Einstein’s General Relativity, which changed how we viewed gravitation, spacetime, and the behavior of the Universe itself. Rather, it was the proof of a greatly underappreciated but profound theorem by mathematician Emmy Noether: Noether’s theorem. The proof showed, for the first time, that if you have a:

• physical system,
• with conservative (equal-and-opposite) forces at play,
• whose “action” has a differentiable symmetry,

then each and every independent differentiable symmetry that it possesses will also lead to an associated conservation law, and a “conserved quantity” by further association.

In simple terms, it means that every time you have a physical symmetry to your physical system, then there’s something physical associated with your system that will be conserved. For example, if your moving system is symmetric under rotations, regardless of how it’s oriented, that means that angular momentum is conserved. This isn’t only true for spherical objects; the Moon orbiting the Earth, and the Earth-Moon system orbiting the Sun, conserve angular momentum as well, because no matter how you orient this orbiting system, the physical rules it plays by don’t change.

The Earth orbits the Sun not in a perfect circle, but rather in an ellipse. The eccentricity, or the difference between the “long axis” and the “short axis” of our orbit, changes over time, while the Earth-Sun orbital period, which defines our year, changes slowly over the lifetime of our Solar System. If we neglect the other planets and the mass loss of the Sun due to the solar wind and nuclear fusion, we’d find that the total angular momentum of the Earth-Sun(-and-moon, if you like) system remains conserved.

Another example is that if your system is symmetric under spatial translations — i.e., changing your coordinate position — then linear momentum is going to be conserved.

So which symmetry leads to the conservation of energy?

That’s the symmetry known as time-translation invariance. It says that the laws of physics, or the rules that particles and fields play by, remain unchanged whether we move any physical system forward or backward in time.

This appears very strongly to be a property of all of our quantum laws of physics, governing individual particles as well as all quantum fields. It governs particles in isolation as well as particles that interact. It governs the creation and annihilation of particle-antiparticle pairs. And it governs every gravitational experiment we’ve ever performed: on Earth, in the Solar System, and even within the Milky Way galaxy. As long as the laws of physics remain unchanged with time for any physical system, then energy is going to be conserved for that system. And that’s true for the strong nuclear force, the weak nuclear force, and the electromagnetic force: always.

A ball in mid-bounce has its past and future trajectories determined by the laws of physics, and only loses energy between bounces due to dissipative interactions of the ball with the ground. In general, if all forms of energy are taken into account, energy is conserved for all four of the fundamental interactions on Earth. In the expanding Universe, however, gravitation experiences a different story.

But it’s only true for the gravitational force sometimes. The reason why is straightforward: for all of the other physical forces in the Universe, the same laws and rules apply at all times, under all conditions, at all locations, no matter what. When things with electric charges move apart, for example, it’s because either some conservative force (like the electric force) is pushing them apart from one another, or some external force is being applied over a distance, performing work on those particles in order to move them. Since work is just another form of energy, and because the equal-and-opposite forces that act on these charges conserve the total (kinetic + electric potential) energy, it’s easy to see that energy conservation still holds.

But for the gravitational interaction, this is only true — under Einstein’s General Relativity — in a spacetime that has a static, unchanging structure with time. If all you had was a single, point mass, the structure of your Universe wouldn’t change over time; it would simply be describable by an exact solution: the Schwarzschild spacetime. If you write down the equations governing this scenario, the coordinates, the laws, and the rules of your spacetime don’t change. Because they’re invariant under time translation, that means energy must be conserved within that spacetime as well.

Both inside and outside the event horizon of a Schwarzschild black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, the gravitational acceleration decreases the farther away you position yourself.

Unfortunately for fans of energy conservation, however, this is no longer true if your Universe expands. In our realistic Universe, the curvature of spacetime is determined by the presence and distribution of matter and energy, and that curved spacetime then tells matter and energy how to move. This works the other way around, too: the presence and distribution of matter and energy defines how spacetime evolves in response to matter-and-energy, and then that evolving spacetime can affect the distribution of matter-and-energy within it as a result.

If your Universe is uniformly filled with matter-and-energy, which our Universe is on the largest of cosmic scales, then the spacetime that describes it isn’t Schwarzschild anymore, nor is it static and unchanging. Instead, that spacetime is known as the Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime, and its most important feature is that it must either expand or contract with time; all static solutions are inherently unstable.

Observationally, we can see and measure that our Universe is expanding, and if that’s the case, then it means that relative positions and distances change over time, and — as a consequence of that — so do energy-dependent quantities that depend on distance, such as gravitational potential energy.

The ‘raisin bread’ model of the expanding Universe, where relative distances increase as the space (dough) expands. The farther away any two raisins are from one another, the greater the observed redshift will be by the time the light is received. The redshift-distance relation predicted by the expanding Universe is borne out in observations and has been consistent with what’s been known since the 1920s.

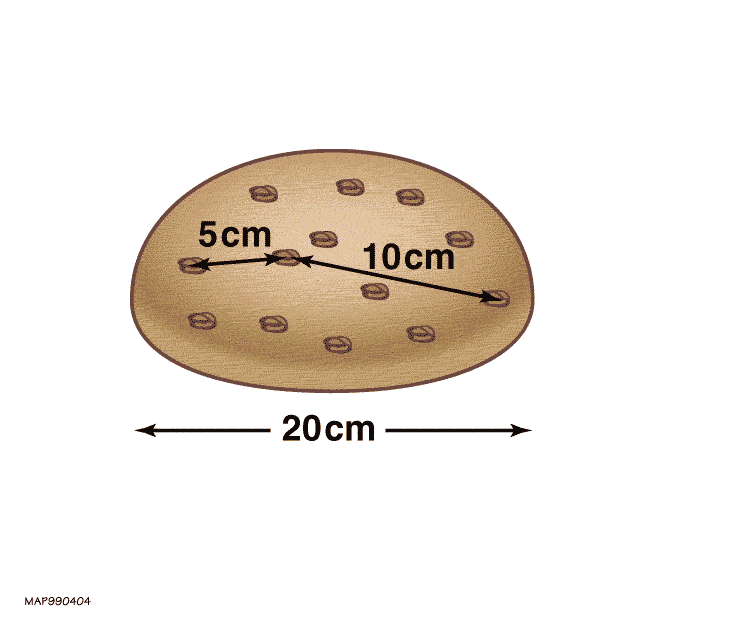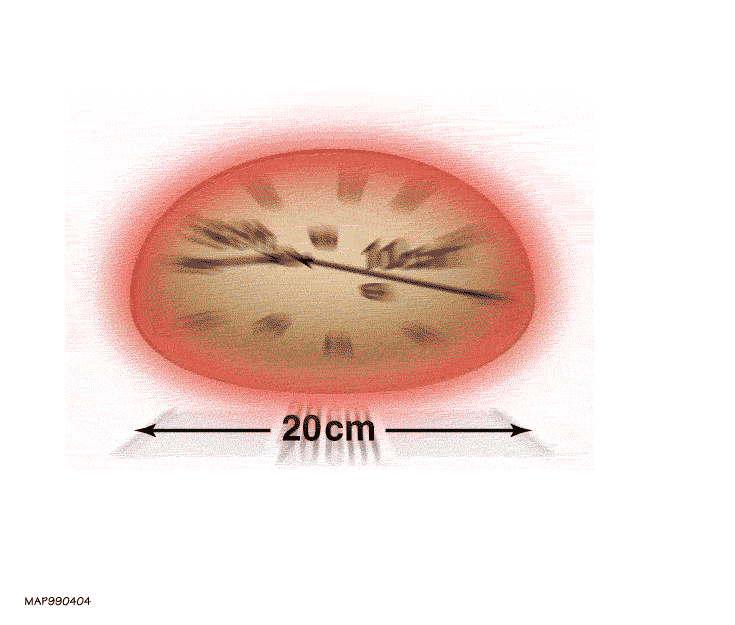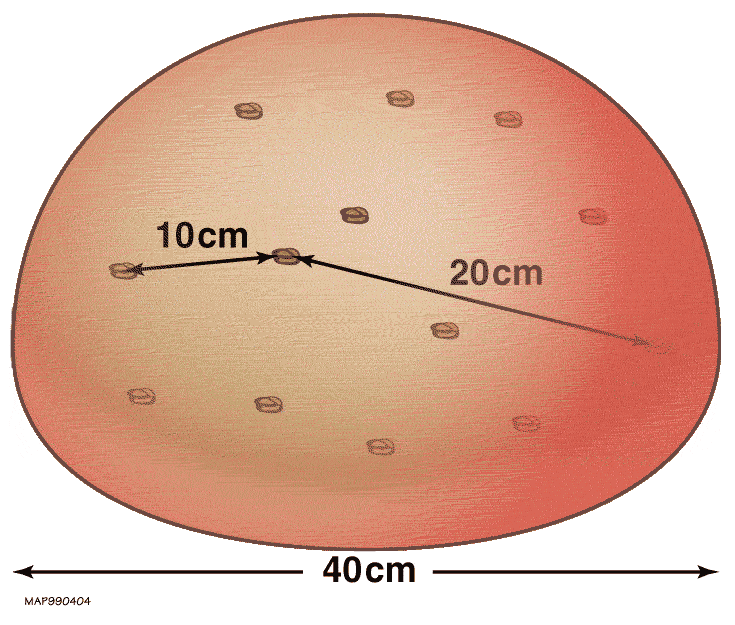
If you have two masses that are gravitationally bound to one another, like we experience here on Earth, it takes some type of work (or other energy input) to successfully pull them apart. It makes sense, in this context, that energy would be conserved: the amount by which you can separate two gravitationally bound masses is directly related to how much energy you put into separating them.

But in an expanding Universe, where we deal with gravitationally unbound systems, the separation of any two masses isn’t related to how much energy gets put into separating them. Instead, the separation between them is really only a function of how much time has passed while the Universe has been expanding, as well as how rapidly the Universe has been expanding over that time. This expansion is “free” in the sense that it doesn’t cost any energy at all; it’s simply occurring over time as a natural consequence of the expanding Universe.

And because the expanding Universe — through the very act of expanding — is no longer the same at all times, that means that it isn’t time-translation invariant, and hence, energy is not conserved.

As the fabric of the Universe expands, the wavelengths of any radiation present will get stretched as well. This applies just as well to gravitational waves as it does to electromagnetic waves; any form of radiation has its wavelength stretched (and loses energy) as the Universe expands. As the fabric of the Universe expands, the wavelengths of any radiation present gets stretched in direct proportion to the “stretch factor,” or how much space itself has expanded.

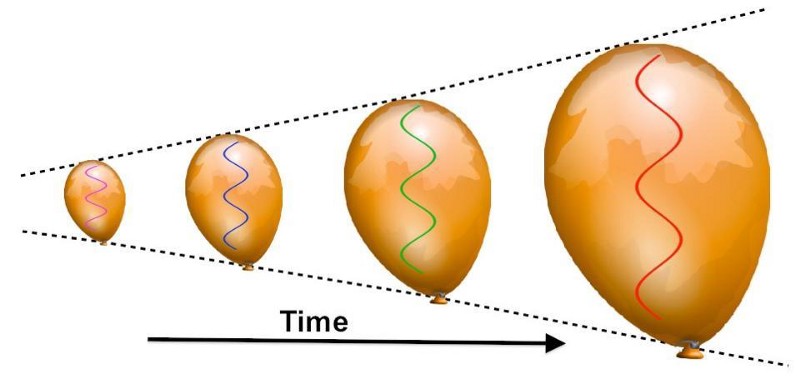
The way that cosmic expansion impacts the energy you’d compute due to matter, moreover, is different than the impacts it has on something like radiation.

If you have a species of matter — i.e., massive particles that have a fixed total mass and that come with a given number of particles that can neither be created nor destroyed — then it’s easy to see how the Universe evolves. We have three different dimensions, and so each time the Universe “doubles” in scale due to expansion, the volume increases by a factor of eight: twice due to each of the three dimensions doubling. As a result, the density drops to one-eighth of its original density, keeping the total “mass” of the Universe constant.

But if you have a species of radiation — i.e., massless particles that have an energy that’s defined by their wavelength, but with a fixed number of particles that doesn’t change — then the Universe will evolve quite differently. Again, we have three different dimensions, and so as the Universe “doubles” in scale, the volume increases by that same factor of eight. But this time, the wavelength of that radiation, as the Universe doubles in scale, also doubles as well, halving the energy of each quantum of radiation. Because these factors compound themselves, the total energy density drops to one-sixteenth of the original, causing the total “energy” of the Universe to decrease by an additional factor of two (the scale of the expansion) relative to the matter-only case.

While matter and radiation become less dense as the Universe expands owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant.

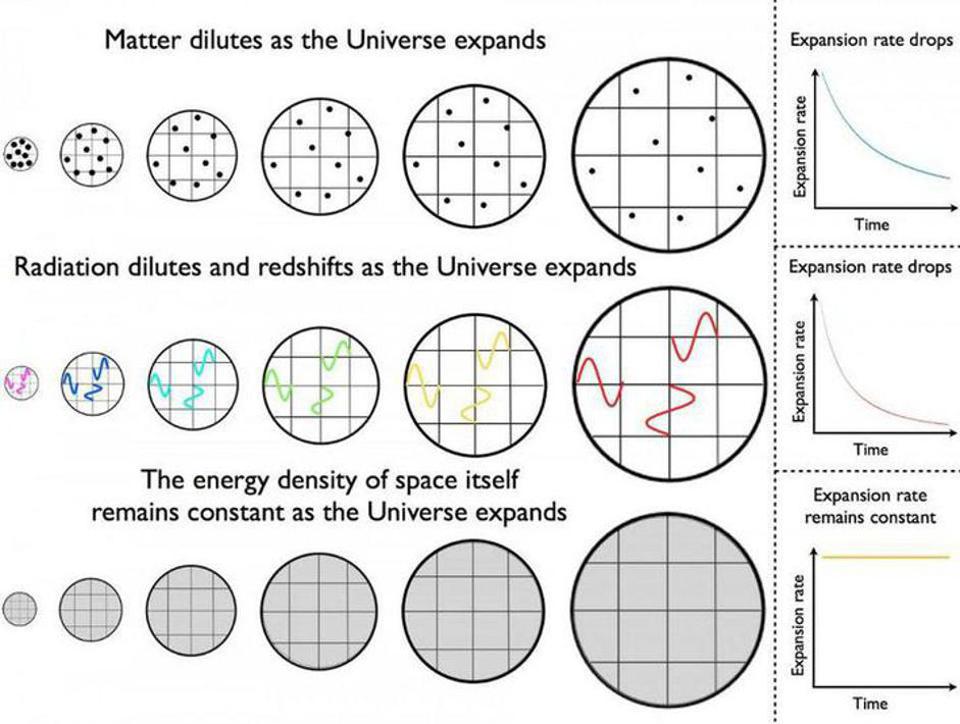
This puzzle gets compounded even further if you then consider what happens in a Universe like our own: where not only matter and radiation are present, but also the mysterious form of energy that’s causing the expansion of the Universe to accelerate, dark energy. Dark energy, to within the limits of our observations, behaves as a cosmological constant, acting like it has a constant energy density irrespective of how much the Universe expands or contracts.

For dark energy, then, as the Universe doubles in scale, the volume of a particular region of space increases by a factor of eight. But because the energy density for dark energy remains constant, that implies the expansion of the Universe has no effect on its energy density at all. As the Universe increases in volume, the total amount of “dark energy” increases as the volume increases: a Universe that’s eight times the volume has eight times the amount of energy in it, and as it continues to expand, the energy within the Universe increases without bound as well. (If the Universe were to contract, instead, that energy would decrease in a similar fashion.)

Just like a ball of dough leavens, causing the various parts of the dough to “expand” away from one another, so too does the fabric of spacetime expand on cosmological scales, driving structures like galaxies, galaxy groups, and galaxy clusters apart from one another. Within these bound structures, however, no expansion occurs.

We can ask, for the case of radiation, “Where did that energy go?” And similarly, for dark energy, we can ask the opposite question, “Where does the ‘new’ energy that appears come from?”

The answer, simply, is that energy is not conserved in an expanding Universe.

“But wait,” you might object, “what about work? Could the reason for the Universe’s expansion be because all the different species of matter-and-energy, whatever they may be, push outward against whatever imaginary ‘boundary’ you draw around the Universe at a particular scale, and that outward push — acting like a force of some type — expands the Universe over a distance, and that force-acting-over-a-distance is work: the form of energy that blows up the Universe?”

And I have to confess, I have a lot of sympathy for this objection. Indeed, it’s possible to concoct and write down a definition of something that is conserved when you do this to the expanding Universe in exactly this fashion. This was accomplished in 1992 in a paper by Carroll, Press, and Turner, where they derived precisely such a definition. In applying it to dark energy, they even stated:

“…the patch does negative work on its surroundings, because it has negative pressure. Assuming the patch expands adiabatically, one may equate this negative work to the increase of mass/energy of the patch. One thereby recovers the correct equation of state for dark energy: P = -ρc². So the mathematics is consistent.“

There is a large suite of scientific evidence that supports the expanding Universe and the Big Bang. At every moment throughout our cosmic history for the first several billion years, the expansion rate and the total energy density balanced precisely, enabling our Universe to persist and form complex structures. Today, dark energy dominates the Universe, while early on, prior to the onset of the hot Big Bang, a phase of cosmological inflation occurred, preceding it and setting it up.

There’s only one problem with this redefinition: it isn’t rigorous or robust; it’s an ad hoc definition. That means that there’s no reason to choose this one particular “global definition” for energy, other than the fact that we have a human bias to say, “Oh, well energy must be conserved, so let’s define it in this one particular way for the expanding Universe.” In reality, the problem with energy conservation in the expanding Universe isn’t that energy is either created or destroyed; the problem is that energy is not uniquely defined in an expanding spacetime. Only if you have time-translation invariance, something explicitly contradicted by an expanding Universe, can energy be defined.

Yes, we could redefine energy in such a way to include the work done by a patch of space on its surroundings, both in positive (e.g., from radiation) and negative (e.g., from dark energy) forms. But the only thing you gain from that is your own personal satisfaction from having concocted a definition that allows this new “thing” to still be conserved in the expanding Universe. But there is nothing useful, extractable, or applicable about this “thing” you’re calling energy; it doesn’t behave like energy in any traditional fashion. The only hope is to go beyond General Relativity’s limitations, and hope that some theory of quantum gravity, yet to be discovered, will allow us to define energy in an expanding Universe, and determine what is — and isn’t — conserved, once and for all!