How to measure a lunar month during the solar eclipse

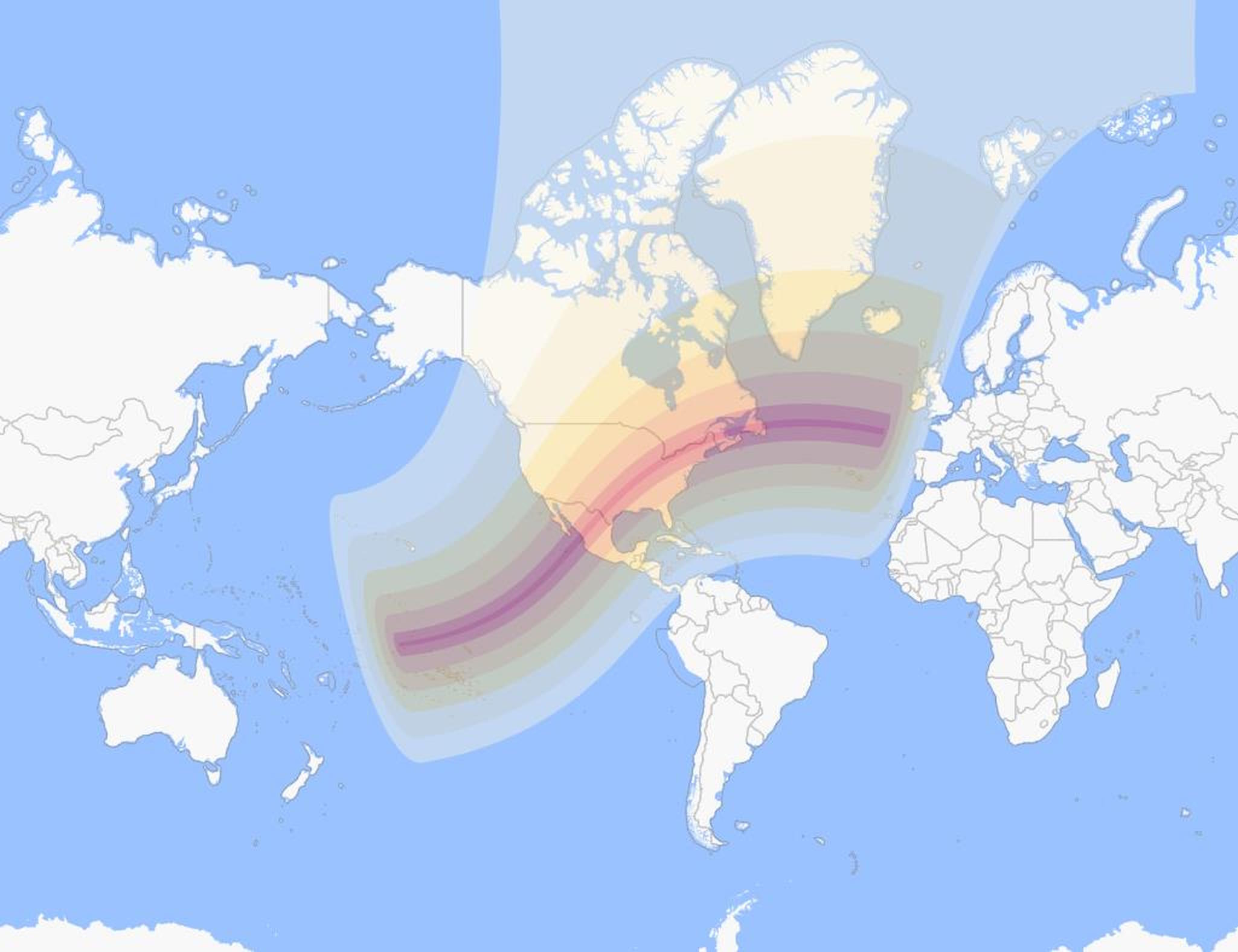
- This April 8, 2024, the Moon’s shadow will fall on Earth: passing across North America, including Mexico, the USA, and Canada.
- Where you either have totality or near-totality (e.g., a 90% or greater maximum eclipse), you can time the duration of the Moon’s motion across the Sun’s disk.
- If you know the angular size of the Sun and Moon, you can use the Moon’s observed motion to figure out how long a full 360° orbit around the Earth takes. The answer is shockingly accurate.
A solar eclipse is a very special physical phenomenon. The Moon orbits the Earth while the Earth-Moon system orbits the Sun, and every so often, all three bodies align. When this alignment occurs when the Moon is on the far side of the Earth from the Sun, we get a lunar eclipse: where the Moon passes into Earth’s shadow. But when the Moon passes between the Earth and Sun and all three bodies line up, the Moon’s shadow can fall onto the Earth itself, creating the phenomenon of a total solar eclipse. To anyone on Earth who happens to be located along the path of that shadow — in the path of totality — it’s an experience unlike any other.
From the perspective of someone on the surface of the Earth in or even just near the path of totality, the Moon will appear to first touch the disk of the Sun at a moment called “first contact,” then will partially or even completely cover up the Sun, and finally will move off of the Sun until the moment of “last contact,” when the full solar disk is exposed bare once again. Remarkably, just by measuring the time from first contact until last contact (even outside the path of totality), plus knowing a few simple facts about the Moon and the Sun, you can to measure the length of a lunar month — or the amount of time it takes the Moon to run once through the full cycle of its phases — to shocking precision. Here’s how to do it.
The reality is that the Earth, Moon, and Sun are always in motion in space.
- The entire Solar System orbits the Milky Way.
- The Sun doesn’t remain stationary but rather wobbles in its position, as the gravitational influence of the planets and other bodies in the Solar System gravitationally influence it.
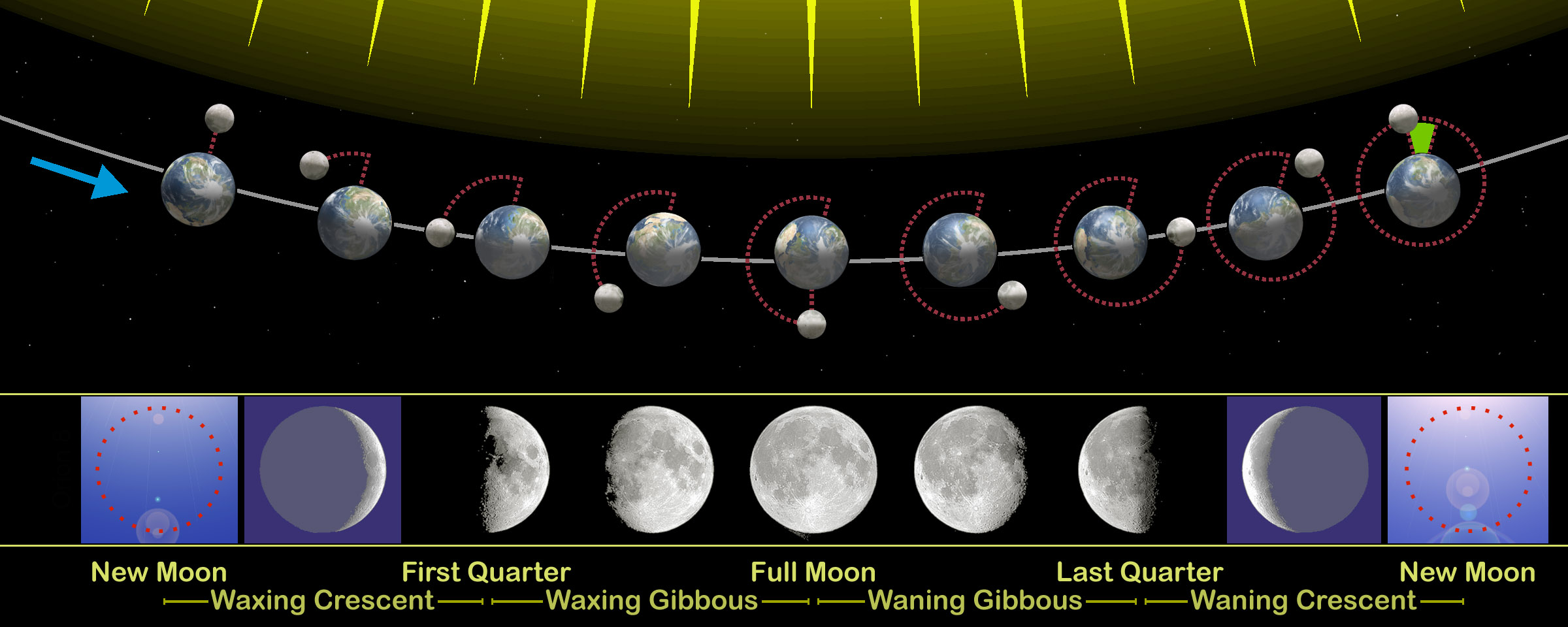
- The Earth doesn’t just revolve around the Sun in an ellipse, but also rotates about its axis continuously, causing every object that we view from Earth to appear to migrate through the sky owing to our planet’s rotation.
- And the Moon also revolves around the Earth in a significantly more eccentric ellipse than the Earth traces out around the Sun, causing the Moon’s revolutionary speed and apparent angular size to change significantly over the course of a lunar month, where the Moon runs through its complete cycle of phases.
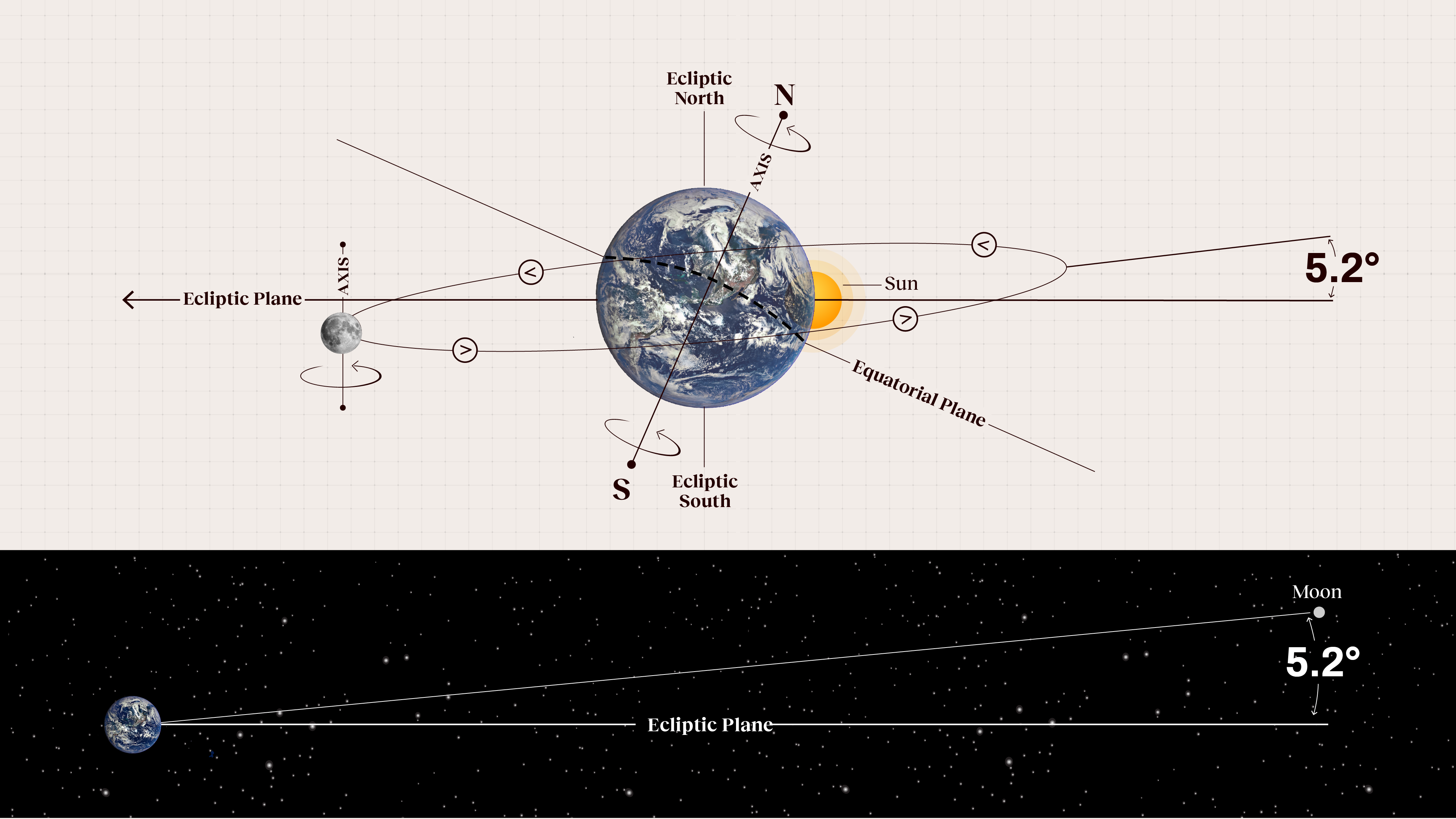
Perhaps most importantly, the Moon orbits around the Earth in a slightly different plane than the Earth-Moon system orbits around the Sun: the two orbital planes are inclined by 5.2° degrees to one another. Even when the Moon is in its new or full phase, only rarely — about once per year for each of the new and full phases — are conditions right that the Earth, Moon, and Sun all line up to make an eclipse occur.

The elliptical nature of these two orbits — the Moon’s orbit around the Earth and the orbit of the Earth-Moon system around the Sun — also has implications for what an observer on Earth sees. While the Moon and Sun may appear to be approximately the same size at all times, the truth is that the angular sizes of the Moon and Sun vary in important ways as seen from the surface of the Earth. Objects appear larger in the sky when they’re closer to us and appear smaller when they’re farther away: differing in angular size from a specific perspective.
Since both the Moon’s orbit around the Earth and the Earth’s orbit around the Sun make ellipses instead of circles, there are variations in the angular size of the Moon and Sun over the course of a lunar month and a calendar year. This matters tremendously when we consider the conditions for a solar eclipse: when the Moon passes directly between the Earth and Sun. When the Moon appears smaller than the Sun, the Moon’s shadow will end before it reaches the Earth, resulting in an annular eclipse. But when the Moon appears larger in angular size than the Sun does, the Moon’s shadow will actually fall on the surface of the Earth, plunging the land on which the shadow falls into darkness during the day: an example of a 100% total eclipse.

However, it isn’t just within the region of totality that one can use a solar eclipse to measure the length of a lunar month. Even outside of the region of totality, there’s a wide “band” of the Earth’s surface that will witness a partial eclipse, and an enormous amount of surface area that will experience a large fraction of the Sun’s disk being blocked at maximum eclipse. For any Earth-dwellers that experience these conditions, the entire duration of the eclipse — beginning at first contact and ending at last contact — will be approximately just as long as experienced by someone located exactly within the path of totality. Measuring this event, from first contact to last contact, is the key to figuring out the length of a lunar month.
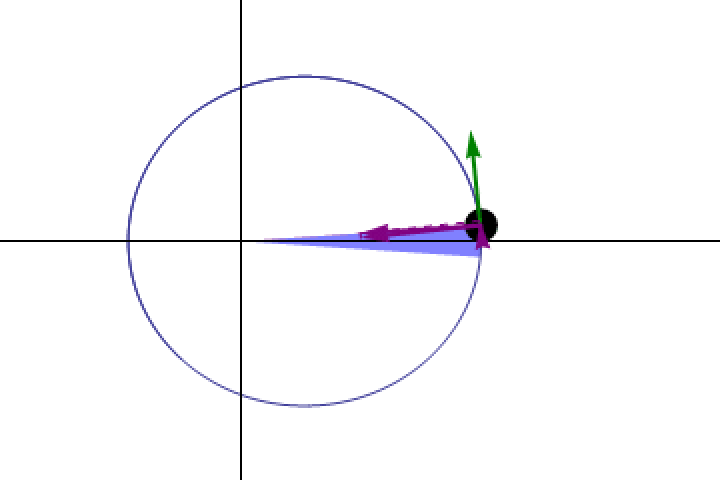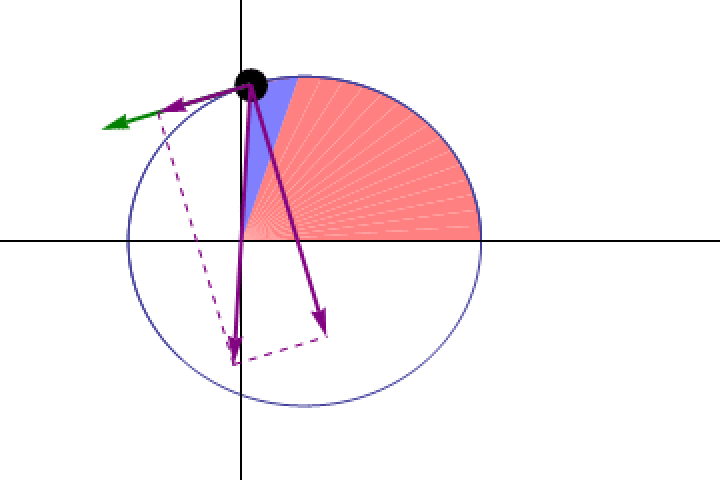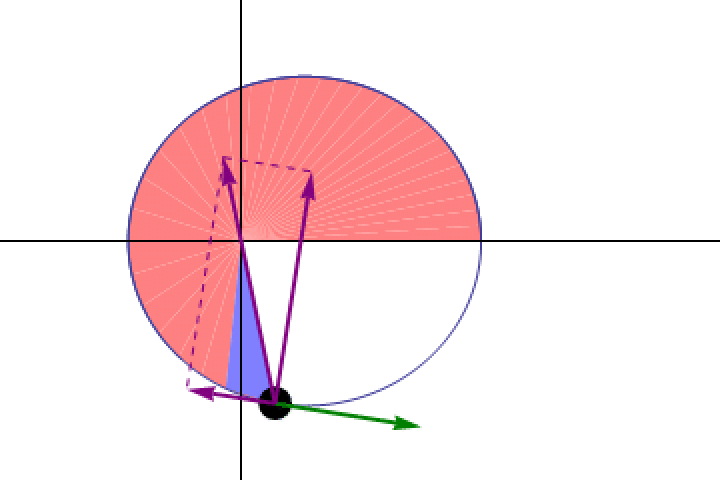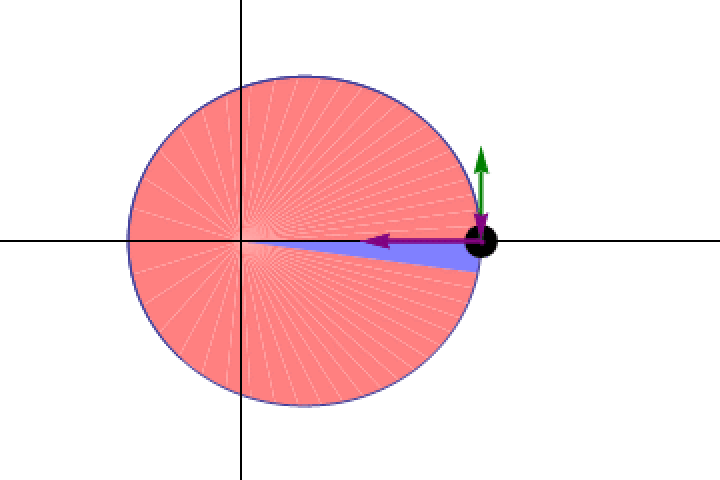
One remarkable aspect of total solar eclipse is that, for someone in the path of totality, because the Sun has an angular size of approximately ~0.5° and the Moon also has an angular size of ~0.5°, the time elapsed from the moment of “first contact” until maximum eclipse corresponds to the Moon moving 0.5° through the sky. Similarly, the duration from the moment of maximal eclipse until the moment of “last contact” corresponds to the motion of the Moon of another 0.5° through the sky. Putting those pieces together teaches us that the duration of the entire eclipse — from first contact until last contact — corresponds to the Moon moving a full 1° through the sky, relative to the Sun.

In order for an entire lunar month to elapse, however, the Moon has to complete a full revolution around the Earth: not just in three-dimensional space, but relative to the motion of the entire Earth-Moon system around the Sun. It’s the light from the Sun that reflects off of the Moon, remember, that determines what lunar phase an observer on Earth sees. As the Moon completes one orbit around the Earth, it goes from:
- a new phase, where the illuminated portion of the Moon faces away from Earth,
- through a crescent phase,
- then a half-full phase (where half of the Moon’s illuminated disk is visible from Earth)
- then a gibbous phase,
- and finally to a full phase (where 100% of the Moon’s illuminated disk can be seen from Earth),
- and then waning to another gibbous phase,
- then back to a half-full phase (where the opposite half of the Moon from the prior half-full phase is lit up),
- then to a final crescent phase,
- before returning to the new phase once again.
Importantly, the length of a lunar month is not just the time it takes for the Moon to move 360° through space around the Earth, but a little bit longer. In order to achieve a “new” phase once again, the Moon must return to the same relative position it was in a lunar month prior: where the Moon has revolved around the Earth by a great enough amount that it makes roughly the same Sun-Moon-Earth line that it made during the previous new phase.
When an observer watches the Moon transit across the Sun during a total solar eclipse, even though it occurs over only a tiny fraction of a single Earth day, that’s the angular motion we’re measuring: the motion of the Moon relative to the motion of the Earth-Moon system around the Sun. From first contact to maximum eclipse to last contact, all told, represents the Moon migrating by about 1° relative to the Sun in the sky. During this event, the Earth still rotates about its axis, but both the Sun and the Moon appear to migrate by the same amount through Earth’s sky due to that effect; the Earth’s rotation cancels out when we make this measurement during an eclipse.
Because of its motion through space and around the Earth, the Moon appears to migrate by a very slight additional amount over time than the Sun, which enables:
- the Moon’s shadow (either umbral or penumbral) to move across the surface of the Earth,
- the Moon to appear to move relative to the Sun from an observer’s standpoint on Earth,
- an observer on Earth to always experience a progression from first contact to maximum eclipse to last contact,
in every solar eclipse that’s visible from Earth. The amount of migration that you see, in terms of angular size, corresponds directly to the angle of migration that the Moon makes in orbit around Earth, relative to its full cycle of phases: as illuminated by the Sun.
Let’s say you go ahead and do this: you find yourself in or near the path of totality on April 8, 2024, and you either:
- put on your eclipse glasses,
- make a projected image of the Sun’s disk and shine it on a surface that displays it prominently,
- or you add a solar filter over the outside lens of your telescope or binoculars,
and you measure the amount of time that elapses between first contact and last contact during the eclipse. You’ll get an answer, assuming you make quality measurements, that last roughly two hours. From the fact that the Moon and Sun each appear to take up about half of a degree in the sky, those two hours correspond to a total of 1° of migration.
If we wanted to use this measurement to make an inference about the duration of an entire lunar month, however, we’d have to realize that a lunar month corresponds to the Moon migrating in a full circle: through a full 360° around the Earth, all relative to the Sun. What we can directly measure during a lunar eclipse is 1/360th of a lunar month, which means all we’d have to do is multiply the duration we measured from first contact to last contact — the duration of a solar eclipse — by 360, and that should tell us how long it takes to account for a full lunar month.

Let’s assume you do this measurement yourself, and you do it extremely accurately. (Note, in practical situations, this is very difficult, as pinpointing the moment of first contact usually only occurs later, given the limits of our senses, than actual first contact occurs. Similarly, your eyes can easily fool you into believing that last contact has already occurred a bit prior to its actual occurrence.) What you’ll find is that the length of the eclipse is approximately 2 hours, or maybe just slightly less if you only have 95%, 90%, or even 85% of totality achieved during maximum eclipse.
Multiply those 2 hours by 360 in order to arrive at the duration of a lunar month: 720 hours total. That’s not normally how we keep track of the duration of months, however, as we prefer to measure things in terms of days. But because we know that there are 24 hours in a day, all we have to do is take our number, 720, and divide it by 24 in order to find the number of days in a lunar month. It turns out that 720 ÷ 24 = 30, implying that there are 30 days in a lunar month. Although there’s a lot of rounding done here, it’s incredible that just by watching and timing the solar eclipse, you can infer the length of a lunar month.
There is the caveat, of course, that this is not a completely accurate way to measure the length of a lunar month. There are three reasons that combine to make this a little bit inaccurate.
- Outside of the path of totality, the geometrical alignment between the Sun and the Moon is imperfect. There is a geometrical difference between the Moon passing through the Sun’s center (tracing out a diameter) versus an off-center position (tracing out a chord), and so anyone outside of the path of totality is measuring a smaller distance that the Moon travels (and a shorter duration for that event) than someone exactly along the path.
- The fact that the Moon’s angular size can be somewhat larger than half-a-degree, especially during a total solar eclipse. On April 8, in fact, the Moon will measure in at about 0.56° rather than 0.5°, and the Sun’s disk is slightly larger than 0.5° as well: coming in more around 0.53°. The duration you’ll measure, from first contact to last contact, will actually correspond to the Moon moving about 1.09° through the sky, implying that you only need to multiply the duration that you measure by 330, not 360, to get the length of a lunar month.
- And there’s also Kepler’s 2nd law, which teaches us that the Moon moves faster than average in its orbit when it appears largest in the sky (closest to Earth) and slower than average when it appears smallest in the sky (farther from Earth), implying that the portion of the orbit you’re watching during the eclipse actually corresponds to a faster-than-average motion of the Moon around the Earth.
Remarkably, the 2nd and 3rd effects partially cancel one another out, meaning that you can always approximate the Moon as moving at the same speed and being the same angular size, and you’ll still come up with an outstanding estimate for the length of a lunar month.
This is a great exercise for middle school or high school teachers (and their students) who are located either along or even simply close to the path of totality. For those in a location where maximum eclipse is 90% or more, multiplying the eclipse duration by 360 still gives an excellent approximation for the length of a lunar month; where maximum eclipse is significantly less, you will calculate a shorter-than-true duration using this method instead. It’s a very easy way to see the approximate connection between something you can directly measure for yourself — the Moon moving across the disk of the Sun — with something that happens on much longer timescales: the Moon going through its full cycle of phases.
It’s no coincidence that, historically, our best methods for keeping time involved the relative motions of the Sun, Earth, and Moon, as these astronomical occurrences are among the most regular events that recur, over and over again, in the natural world. Eclipses were first understood at least as early as the time of the Babylonians some ~3000 years ago, who knew how to predict precisely where and when eclipses would occur. Through the combination of a little astronomy and a little geometry, any observer can calculate the approximate length of a lunar month simply by watching a solar eclipse. Now, you can, too.