Ask Ethan: Could we build a collider bigger than Earth?

- If you want to collide the largest number of particles at the highest possible energies, you’ll want to build a circular particle accelerator and collider: similar to the Large Hadron Collider (LHC) at CERN.
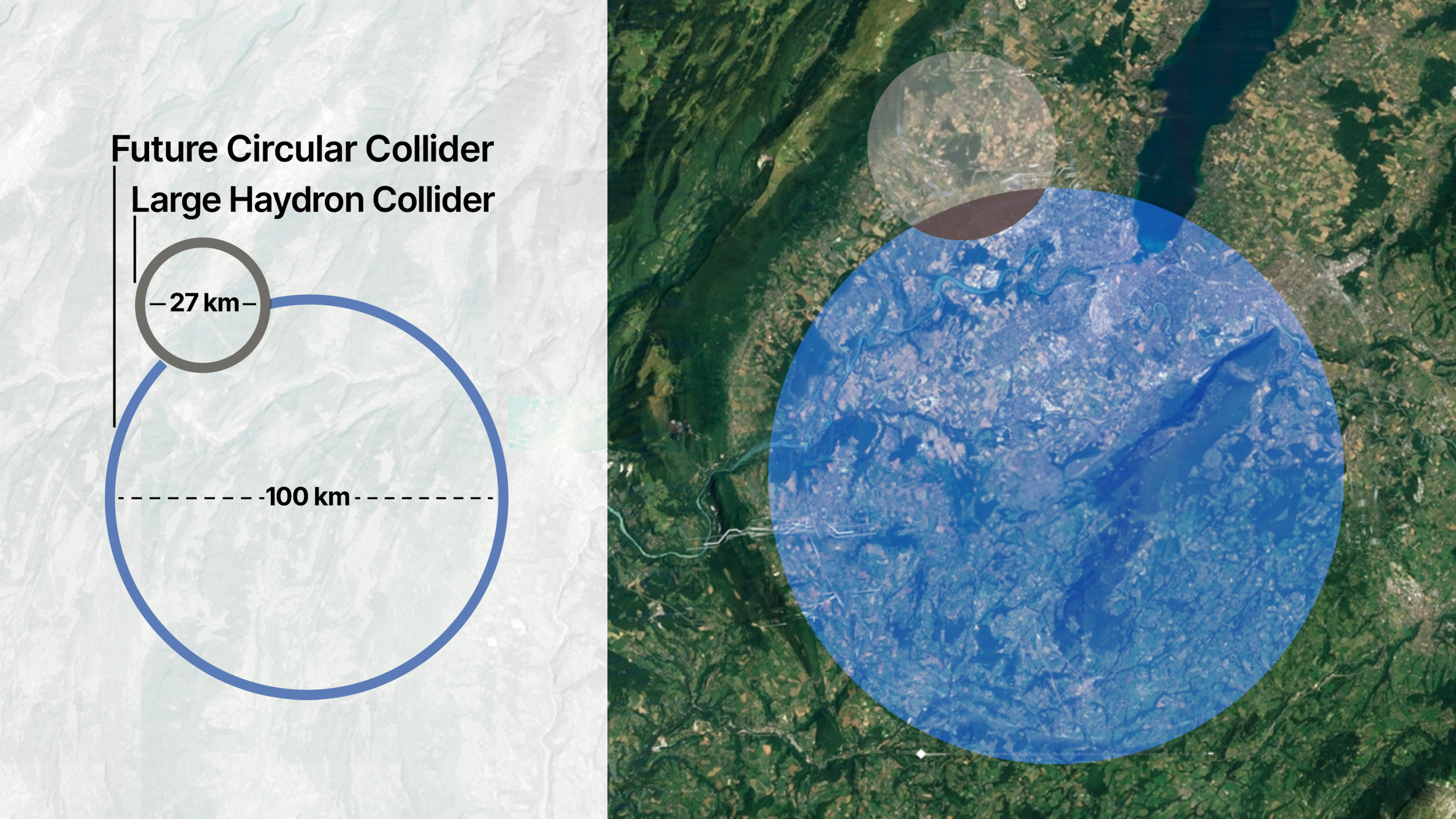
- The LHC is the largest particle accelerator ever built on Earth, with a circumference of around 27 kilometers. However, we can imagine building far larger ones, including ultimately, around the equator of Earth itself.
- However, some have envisioned even grander particle accelerators, which could reach the most extreme energies of all-time, by building them in space. We’d gain so much, but is it truly feasible?
The Large Hadron Collider (LHC) is the largest, most powerful particle accelerator ever built on Earth. Accelerating protons up to energies of ~7 TeV apiece — to energies about 7000 times greater than their rest-mass energy as given by E=mc² — it smashes protons circulating clockwise with protons circulating counterclockwise into one another at specific collision points, where giant detectors then measure the debris emerging from those collisions and attempt to reconstruct them in an effort to probe fundamental physics. After announcing the discovery of the Higgs boson in 2012, it continues to probe the subatomic universe to the highest precisions of all-time.
But in order to push the frontiers of physics even further, a new, more powerful machine will be required: a future particle collider. Although there are four main concepts currently being considered, there are many who ultimately hope for a particle accelerator the size of Earth, or even greater. That’s what Gary Camp has been thinking about, as he writes in to ask:
“Since bigger is better (so far) I am toying with the idea of a collider that circles the Earth. Many advantages are there as well as problems. If you can make a sun shade efficient enough, there is little need for cryogenic cooling of magnets since space is very cold without the sun. Earth magnets need to be quite strong due to the tight radius of the collider but much smaller in Earth’s orbit. Solar power may be enough to power each magnet or it may be necessary to use the new small modular Nuke generators which might be made more cheaply in quantity and perhaps less shielding required. DOD might want to contribute to the development as they want that portable/remote generator badly.”
There are a great many reasons to want to build a collider either around the Earth or in space, but “cheaper” isn’t one of them. Here’s what we should all be considering when it comes to particle accelerators.

Although we might not think about it this way, all particle accelerators begin with plain old particles at rest: particles that are bound together conventionally, in the form of atoms. We then take a successive series of steps to accelerate them up to high energies and relativistic speeds, which generally include:
- ionizing the original (normally, hydrogen) atoms, breaking them up into electrons and nuclei (typically, single protons),
- subjecting those particles to a strong electric field, which accelerates them since they’re charged particles,
- using electromagnets to collimate these now faster-moving particles, creating a “beam” out of them,
- and then using electric fields to accelerate these now-collimated particles up to the highest energies we can muster.
What’s vitally important to keep in mind is that there are only two collider layouts that can efficiently get you to the highest energies. Either you can build a linear collider based on light particles, like electrons and positrons, where you built a long “track” with a continuous electric field to reach the greatest possible energies by the time you arrive at the collision point, where your detector is then built, or you build a circular collider, which recirculates the particles — either electrons-and-positrons, protons-and-protons, or other leptons or hadrons — both bending them and periodically “kicking” them to higher energies, continuously, until they’re ready to collide.

Why is this important to keep in mind? Because, for circular colliders, which are the only realistic option for bringing particles with heavy rest masses up to very high energies, this means we can’t use permanent, fixed magnets to bend these particles, but must instead use electromagnets.
This is a very important consideration when it comes to the design of a particle accelerator. If you want to bend a charged particle into a circular path, the best tool we have for that is a magnetic field: electrically charged particles in motion will be bent into a circular path by a magnetic field that’s perpendicular to the particle’s motion. When the particles first enter the circular accelerator, however, they’re not all the way up at their maximum speed just yet; they’re moving much slower and at much lower energies than that, as they’re “only” at whatever energy they were accelerated up to prior to being injected into the main, final accelerator ring.
That means you need to start off with a relatively low magnetic field, and then each time you kick the accelerated particles up to higher and higher energies, you need to increase the strength of the magnetic field to keep that particle bending in a circle of constant radius. At greater and greater energies, you need stronger and stronger magnetic fields to keep that particle confined within that ring, otherwise it will simply smash into the accelerator walls.

At CERN, at Fermilab, and at other circular accelerators, this has been the preferred design of the particle accelerator for many decades. You use smaller accelerators, either circular or linear or a combination of both, to prepare bunches of particles that are:
- high in number and in number density,
- collimated together as tightly as possible,
- and injected into the main accelerator ring at the highest initial energies possible,
before they’re brought up to the highest final energies just before they’re collided with particles circulating within the same ring in the opposite direction.
Electromagnets are a key tool in all circular particle accelerators, as the bending magnets keep the particles moving in the exact circular path required, while collimating electromagnets (e.g., quadrupole and octupole electromagnets) prevent those particles — which, remember, there are many of and are all of the same electric charge — from repelling one another so significantly that they’d spread out and crash into the accelerator walls. Meanwhile, an applied electric field, often leveraged during an inserted “straight” segment of the accelerator, will give a “kick” to each of these particles whenever they pass through it, speeding them up just a tiny bit closer to the speed of light and bringing them up to higher and higher energies.
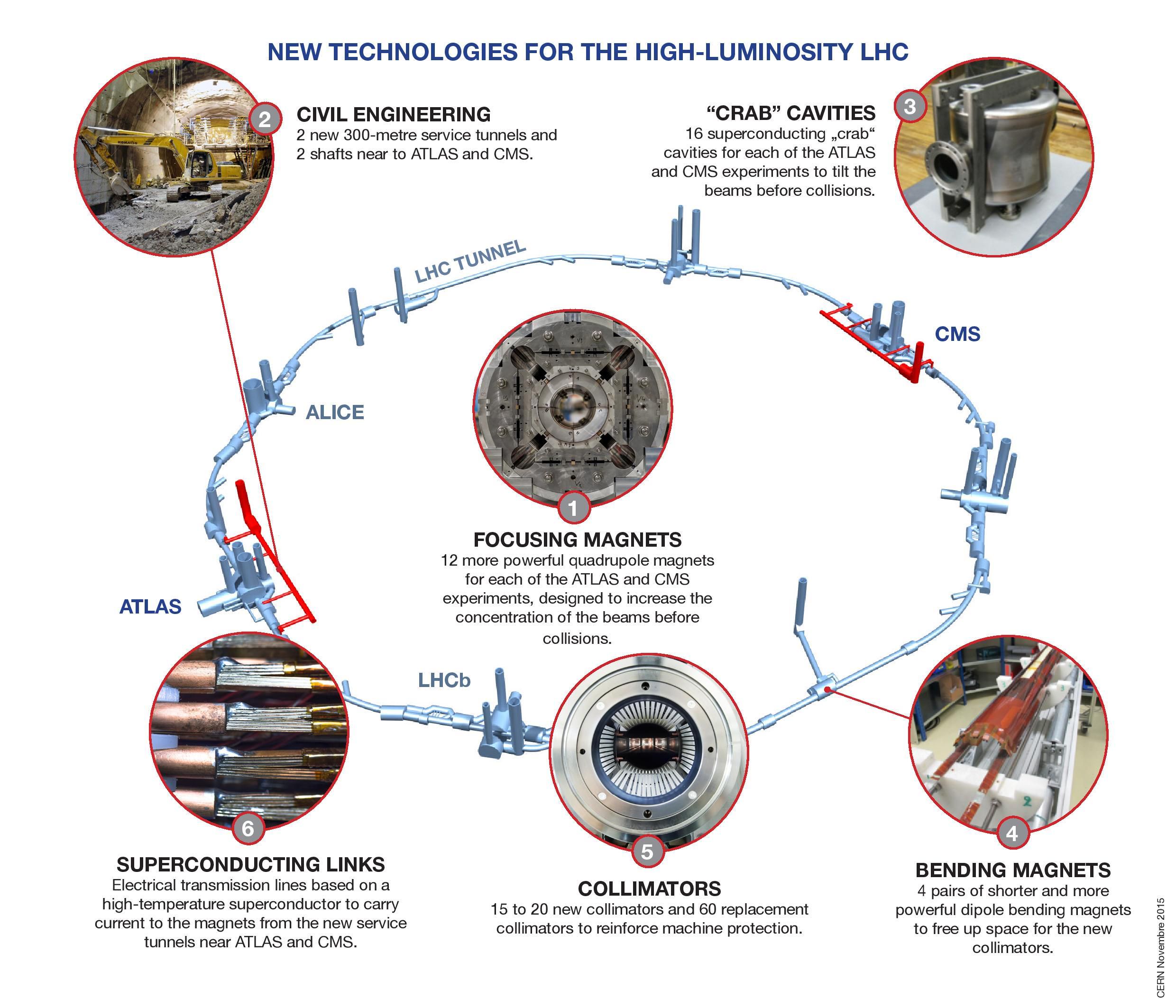
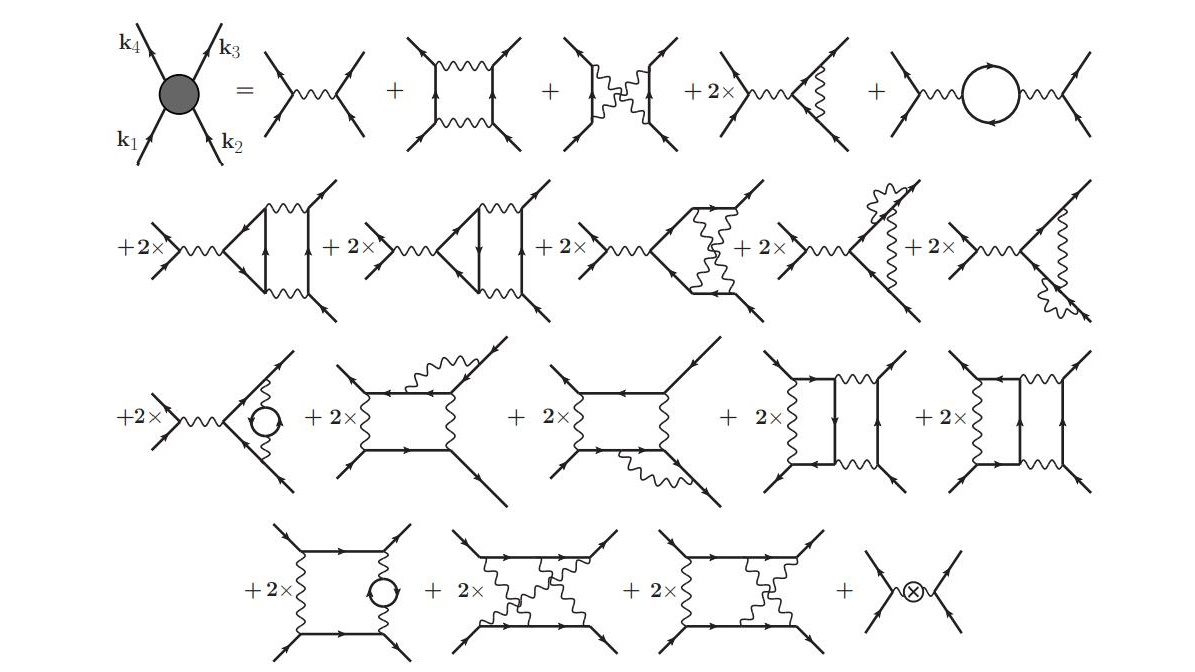
It’s important that we understand these components of an accelerator design, because if we want to build a very large accelerator, we want to do it as efficiently and effectively as possible. Ultimately, the maximum energy that your (circular) accelerator can reach is determined only by three factors.
- The strength of the magnetic field, and specifically the maximum strength of the bending magnets, that keep the accelerated particles confined to the relevant circular path. Stronger bending magnets translate to higher maximum energies.
- The physical size of your accelerator, and specifically the radius of the circular path that the particles trace out, is also a limiting factor. As you double the radius of your accelerator, you double the maximum energies that it can achieve.
- And finally, there’s the problem of synchrotron radiation, which is energy that gets radiated away, electromagnetically (in the form of photons), anytime you accelerate a charged particle in a magnetic field. This radiation most strongly limits particles with a high charge-to-mass ratio, like electrons or positrons, but is much weaker for heavier particles, like muons or protons.
If you want to build the most powerful particle accelerator you can — which is, in fact, what we want to do — you’ll want to maximize the magnetic field strength and the accelerator ring radius, while minimizing the impact of synchrotron radiation.
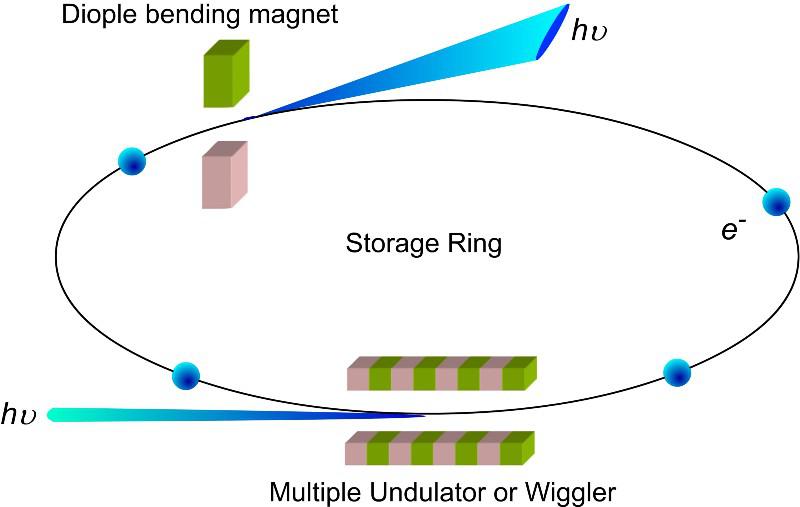
At present, the LHC boasts the strongest bending magnets (at around 8 T) and the largest radius (of about 4.3 kilometers) of any accelerator ever constructed. Prior to the LHC, however, which collides protons with protons, that same tunnel held an electron-positron collider known as LEP: the Large Electron-Positron collider. Even though LEP was the same size as the LHC, the LHC’s protons were accelerated to about 7 TeV of energy apiece, while LEP struggled to get its electrons and positrons up past 100 GeV (just 0.1 TeV) of energy. The culprit, as you might have guessed, was synchrotron radiation.
Fortunately, for the same size ring, a proton emits just one-ten trillionth (one part in 1013) of the amount of synchrotron radiation emitted by an electron, so although electron (and positron) energies are very limited by circular accelerators, this isn’t the case for protons at all. In fact, synchrotron radiation can be lowered by building larger and larger radius rings, so if we’re simply willing to go bigger and bigger, we could — at least in theory — go all the way up to the Planck scale of ~1019 GeV with a large enough circular accelerator. It might take an accelerator significantly greater in size than the Solar System, or even the Oort cloud, in order to do it, but it’s at least theoretically possible.

The reason all of this is important is because it tells us what we need to consider if we want to build the largest, most powerful accelerator we can conceive of. Originally, back in the ~1950s, legendary physicist Enrico Fermi (for whom Fermilab is named) suggested building a particle accelerator around the equator of the Earth. (When I first heard about this idea, the physicist who presented it to me named it the “Fermitron,” although I have not heard that name since.) With a radius of 6378 kilometers, or a radius that’s approximately 1500 times the radius of the LHC, we could leap from collider energies of around ~14 TeV up to collider energies that are more like ~20 PeV, where a PeV is a peta-electron-volt, and is equal to 1000 TeV or 1,000,000 GeV.
However, that’s only the case if we keep the same-strength bending magnets that we find at the LHC. If we wanted to spend less on infrastructure, we could use conventionally (or passively) cooled electromagnets, rather than the superconducting electromagnets that are actively cooled with liquid helium, leveraged both at the modern LHC as well as Fermilab before it. However, those electromagnets are limited to be much weaker than the LHC’s magnets, and can only achieve field strengths of around ~1-1.5 T, rather than the ~7.5-8 T achieved at the LHC. That loss of capability at the energy frontier is in no way “made up for” by having a less expensive set of electromagnets that don’t require active, liquid helium cooling. In fact, the expense of a larger ring far outweighs the cost savings by using cheaper electromagnets.

Instead, it’s worth looking in the other direction: at the ultimate capabilities of magnets. You might have learned that permanent magnets can be powerful, and indeed they can. The strength of Earth’s magnetic field is normally measured in units called “gauss,” where 1 gauss (or 1 G) is just one-ten thousandth of 1 tesla (or 1 T). Earth’s magnetic field is around 0.6 G at the surface. However, permanent magnets can hold a maximum magnetic field of around 14,000 G, which is 1.4 T. However, electromagnets can far exceed that, with the bending magnets at the LHC reaching ~8 T and experimental electromagnets at, for instance, the National High Magnetic Field Lab, creating magnets for various purposes whose field strengths range from 25-45 T, and may yet reach even greater magnitudes.
What’s vital to remember is this: the energy of your (proton-proton) collider is directly proportional to the strength of the magnetic field you can achieve. If we could, for instance, upgrade the LHC’s electromagnets to be double, triple, or quadruple the strength of the electromagnets within it today, we could double, triple, or quadruple the energy reach of the entire machine. The reason the LHC is so much more powerful than Fermilab’s Tevatron, which preceded it, isn’t just because the LHC is a larger machine; it’s also because the LHC has stronger bending magnets than the Tevatron ever had: almost double the field strength, in fact.
It is important to remember that particle accelerators aren’t just machines where you can, “Give me a big ring and a strong magnet, and I’ll give you high energy particles.” Instead, you need a precise machine, all the way through, that has the ability to bend, collimate, and accelerate particles progressively, from low energies all the way up to the highest energies your accelerator can possibly achieve. This takes a lot of infrastructure, coordinated electronics, liquid helium cooling for your electromagnets, and substantial amounts of shielding for your accelerator. At higher and higher energies, you also have to deal with radiation that may be potentially hazardous to living things, like human beings.
You cannot get there with passive cooling; you cannot get there with small amounts of power or energy; you cannot get there with either permanent magnets or Earth’s natural magnetic field. All of this is much easier to perform on the surface of the Earth, where nearly the entirety of all human infrastructure ever assembled is built, and with sufficiently strong electromagnets, we may yet be able to reach up to around the ~100 PeV mark (or ~108 GeV) in terms of collision energy with an Earth-circling particle accelerator. It’s an incredibly ambitious and incredibly expensive proposition, but with sufficient technology and resources, it’s potentially realistic to have a machine that reaches up to around 10,000 times the current energy limits of the LHC.
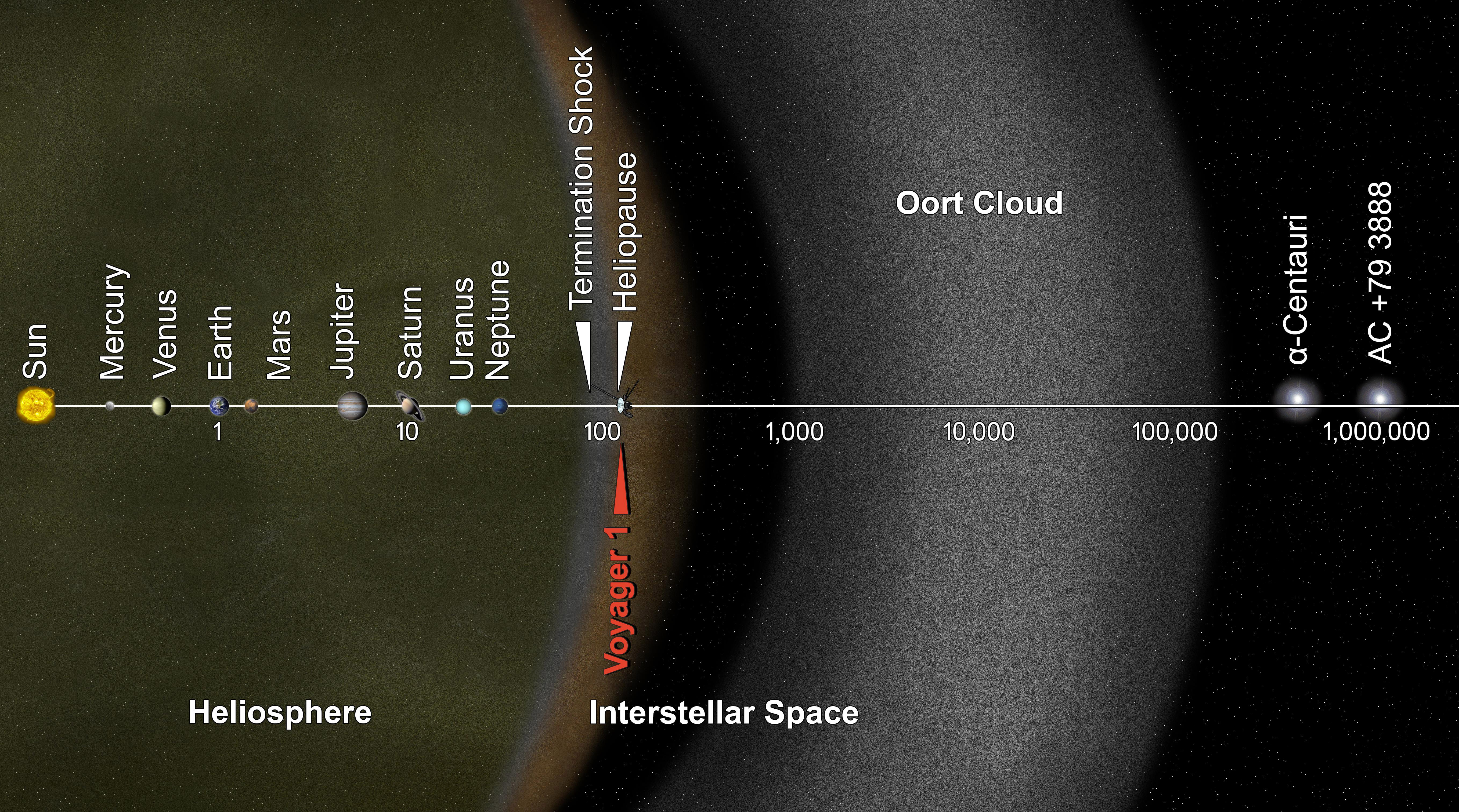
However, it’s worth noting that the energy scales we’re truly interested in reaching are way, way up there. The maximum energy of the highest-energy cosmic rays generated naturally are around 1011-1012 GeV, and that would require an accelerator the size of Earth’s orbit around the Sun. The theoretical scale for grand unified theories is up around 1015 or 1016 GeV, which would require an accelerator that isn’t the size of Earth’s orbit, but rather is 1000 to 10,000 times as large: between 1000 and 10,000 A.U. in radius. If we achieved those energies, we’d potentially have to begin wondering whether we might “accidentally” trigger a Universe-destroying catastrophe, as that’s also the theoretical energy scale at which cosmic inflation occurred. Restoring the inflationary state would conceivably cause the space where it occurs to expand, both rapidly and relentlessly, and could easily unbind planet Earth from the Sun.
At even greater distance scales, we could imagine an accelerator that was up to ~100 light-years in size: one that was big enough to reach Planck energies, or the energy scale at which the laws of physics themselves are known to break down. It might seem like a daunting task to coordinate different parts of an accelerator that cannot be coordinated from a central location even at the speed of light, but someday, if experimental particle physics ever advances that far, that will be the least of our worries. So far, that’s the only idea we have to directly test string theory, and admittedly, it’s not exactly practical. Nevertheless, these types of big dreams, while implausible today, may someday inspire future generations of humans to probe beyond any frontiers we can even fathom today. After all, the entire subatomic universe still awaits.
Send in your Ask Ethan questions to startswithabang at gmail dot com!