Ask Ethan: How do photons mediate both attraction and repulsion?
- In our Universe, photons, or the quantum particles that make up light, are profoundly important not only for life and energy, but for fundamental physics as well.
- The photon is the particle that mediates the electromagnetic force: responsible for the attraction of oppositely-charged particles, the repulsion of like-charged particles, and the magnetic bending of charged particles.
- How does one particle, with no charge of its own, create all of these forces in different directions when it’s “exchanged” between different charges? Physics holds the answer.
In our Universe, photons are one of the essential ingredients to matter — and life — as we know it. Light of all types (visible, infrared, ultraviolet, etc.) is made up of photons, and photons can be absorbed or emitted by charged particles, including within atoms, allowing for all sorts of vital processes and phenomena like photosynthesis, radiation, and even what we perceive as “color.” But photons serve another function that’s more fundamental: they themselves are the particles that mediate the electromagnetic force. When charged particles attract, repel, or are bent in a magnetic field, it’s the photon that does the heavy lifting, as it’s the underlying cause behind all of these interactions.
So how is it, then, that this one species of particle, which happens to be both massless and electrically neutral, is responsible for all of these phenomena? How can “exchanged photons” do it all: cause attraction, repulsion, or a perpendicular bending force? That’s what Jon Joseph wants to know, writing in to ask:
“The electromagnetic force is mediated by photons. And unlike all other forces, the electromagnetic force can be either attractive or repulsive depending on the sign of the charges involved. What is the difference between those virtual photons that mediate the attractive electromagnetic forces versus the repulsive electromagnetic force? Don’t photons come in essentially one flavor?”
Photons do only come in one flavor, and yet they are responsible for all of these manifestations of the electromagnetic force. In order to understand how, you very likely have to be prepared to revolutionize how you view reality.

The first thing you have to understand is that, when it comes to the light (photons) we’re familiar with, we’re referring to real particles. Real, in this sense, has a very specific set of meanings.
- “Real” means that the photons that we’re talking about carry positive, finite amounts of energy.
- “Real” means that the photons have a momentum inherent to them: momentum with both a magnitude and a direction.
- “Real” means that the photon has a point-of-origin: a location in space and a moment in time where that photon was emitted as a result of an interaction involving at least one other particle.
- And “real” also means that, when that photon has an interaction that leads to its absorption, the quantum particle (or system of particles) absorbing it will have to deal with the addition of both the energy and momentum that the photon was carrying, which will remain conserved when considering the overall system.
When you feel the warmth of the sunlight, see objects illuminated by moonlight, or detect the color of the pixels on the screen that you’re reading this text on right now, you are experiencing the effects of interacting with real photons. The photons that travel through space, that are seen by our telescopes, and that cause electrons to be kicked off of atoms via the photoelectric effect, are all examples of real photons.
On the other hand, when you talk about the photons that mediate the electromagnetic force, those photons aren’t “real” at all, but rather are a different type of particle: virtual particles, or in this case, virtual photons. This concept only arose when we began to replace our classical picture of the Universe with a quantum one: when we went from a description of forces as being derived from smooth fields that permeated all of space to being derived from quantum fields and the exchange of quantum particles.
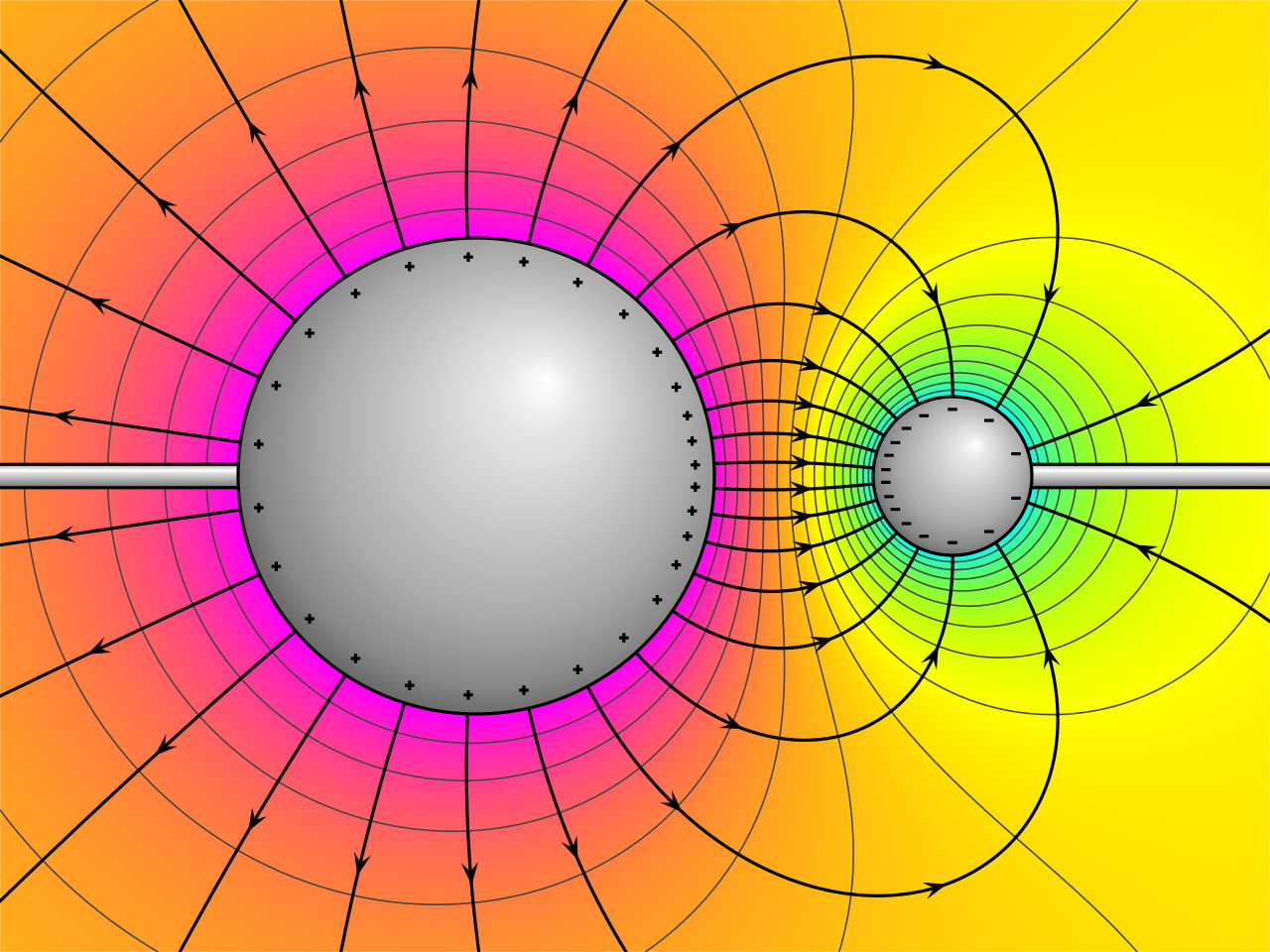
Classically, if you think about the electrostatic force (the force generated by one or more charged particles at rest), you’d simply draw a series of electric field lines — lines that moved “outward” from positive charges and “inward” toward negative ones, where field lines always intersect these charges at perpendicular angles and where the density of field lines corresponds to the strength of the field at that location — and then note that the force on any particle would equal the charge of that particle multiplied by the electric field at its location.
Something very similar would also be at play for classical magnetic forces, except that in this case the strength and direction of the magnetic force wouldn’t be in the direction of the magnetic field, but perpendicular to it: proportional to the charge and speed of the particle experiencing the force, as well as the angle between the particle’s velocity and the magnetic field lines at that location.
When we move into the territory of quantum physics from classical physics, however, this picture needs to change. After all, in our Universe it isn’t just the particles that are quantum in nature, but the fields as well must be treated as quantum entities.
This is a huge change! Many of us can visualize quantum particles pretty easily: instead of treating matter (or any form of energy) as continuous, you treat it as being made up of an enormous number of discrete entities. Instead of treating water as a fluid, you treat it as a collection of a tremendous number of tiny particles: molecules. Instead of treating the Sun as a hot plasma, you can treat it as a collection of electrons and ionized atomic nuclei. And instead of treating light as a continuous series of waves, you can treat it as an enormous number of discrete, individual photons, where each photon has its own unique properties (i.e., energy and momentum).
But how do you go from treating fields as a classical entity to treating them as a quantum one? The most common visualization of these fields is shown below, and is shown for empty space, with no “sources” (or charged particles of the relevant type) inside of it. Instead of fields being smooth and continuous and static, we now view them as being variable from place-to-place and in time, fluctuating in random, unpredictable ways.

Encoded in visualizations such as these are the notions of quantum uncertainty — particularly of the energy/time uncertainty variety — as well as of field fluctuations. However, these visualizations, along with others that commonly show particle-antiparticle pairs “popping” out of empty space, don’t tell us anything about how quantum fields work as compared to classical fields. They simply show how our classical view of empty space is incomplete, and attempt to illustrate one or more aspects of what our traditional “empty” views of empty space overlook. (Unfortunately, often bringing more unwanted misconceptions along with them in the process.)
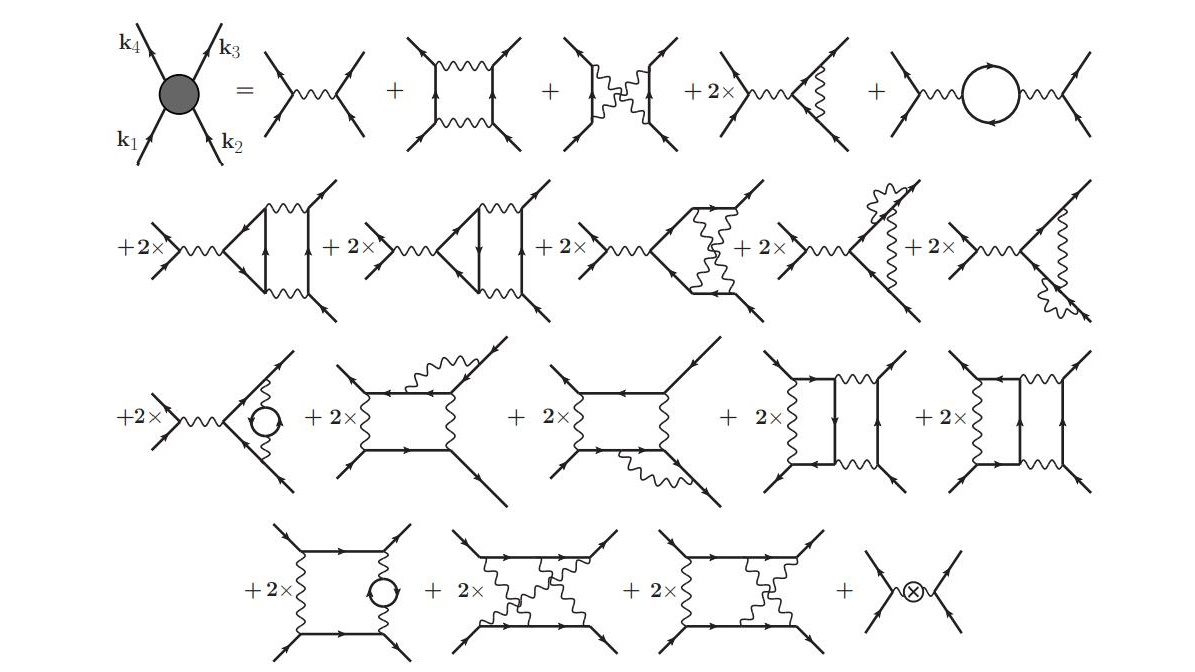
The way that physicists — and, over time, laypersons as well — normally visualize the interactions between quantum particles is instead to make use of a very different visualization technique: the use of what are known as Feynman diagrams. In Feynman diagrams, we treat individual particles as quantum entities, such as electrons or quarks, and display them as solid lines with arrows that indicate the direction of their propagation. Then, between these particles, there are forces that are “exchanged” between them, and those forces are treated differently: as wavy, squiggly, or dotted lines that connect two (or more) particles to one another at each vertex.
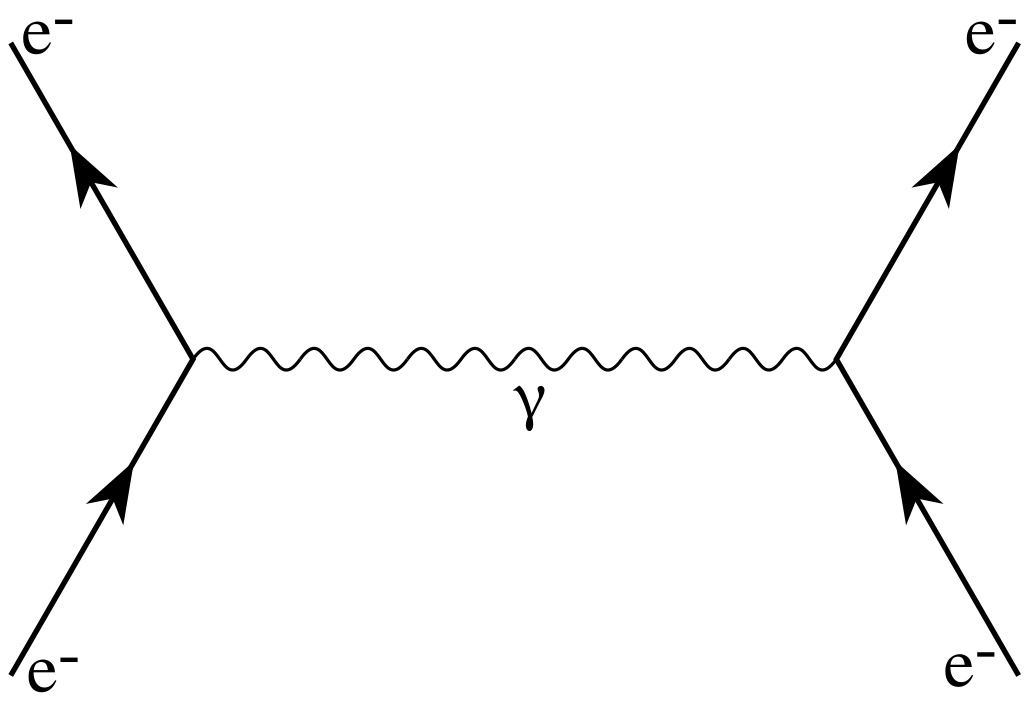
In this picture, the “exchanged” particles aren’t real particles, but are merely virtual particles, like virtual photons, gluons, or W-or-Z bosons. When you look at diagrams like the one shown above, it’s easy to see where the initial question comes from. After all, it looks like what’s happening is as follows.
- You have a particle, like an electron, that exists with some amount of motion inherent to it.
- Then, all of a sudden, that electron emits one of these bosons, which means the electron should recoil opposite to the direction the boson (in this case, the photon) was emitted in.
- Next, that boson (in this case, the photon) gets absorbed by another charged particle (in this case, another electron), where that electron should have its motion changed by that absorption to move closer to the same direction that the photon was traveling.
- And finally, the two “real” particles, or the two electrons in this case, wind up experiencing a net repulsion, mediated by the photon that mediates the electromagnetic force.
Looking at the picture of Feynman diagrams and putting together what most of us know about electrons and photons (and momentum conservation), it’s easy to see how one would look at this and think that “repulsion” is natural, but “attraction” or “magnetic bending” is difficult to understand. But this fundamentally misunderstands what it is that these Feynman diagrams are actually encoding.

What Feynman diagrams show isn’t, in fact, related to the strength or direction of an interaction in any sense. All Feynman diagrams illustrate is:
- which particles are interacting (the electrons in this case),
- which particles are being exchanged as part of the interaction (the photon in this case),
- and where those interactions occur (at the vertices between each electron and the photon in this case).
Everything else that you “see” in the diagram, like which direction the particles go off in, is meaningless.
This is something that you learn whenever you study quantum field theory in your training to be a physicist, but it’s something that practically all non-physicists are never exposed to. The important part of Feynman diagrams for performing calculations is knowing which particles are interacting, which particles are being exchanged as part of that interaction, and where the interactions (i.e., vertices) are and what’s happening between them. Although we considered this for a diagram that looks like a “stick” initially, the power of Feynman diagrams is that it allows you, simply by drawing these graphs appropriately and exhaustively, to draw and collect all of the allowable diagrams that have no loops in them (tree-order diagrams), one loop, two loops, etc., which enables you to perform progressively more and more accurate calculations as you expand to higher and higher loop order.
The reality is that these forces, mediated by the bosons in our illustrated Feynman diagrams, can always be of either sign: positive or negative. What determines that? For electrostatic forces, it’s whether the charge “signs” on the particles that are exchanging the photons are like (positive-positive or negative-negative), which leads to repulsion, or opposite (negative-positive or positive-negative), which leads to attraction. Other forces, like the strong nuclear force, turn out to always be attractive (or zero); it’s never negative. If we ever came up with a quantum theory of gravity, it would also turn out to always be attractive (or zero), as there’s no such thing as a negative gravitational charge (negative mass or negative energy) in nature.
The only apparent paradox that we see arises because of our initial misconception: that these real particles (i.e., the electrons) are somehow emitting and exchanging real photons — photons that carry real, positive amounts of energy and momentum — between them. But that’s not true, because these aren’t real photons that are exchanged, but virtual ones. These photons don’t exist in the conventional sense: if you placed a detector between two electrons that were repelling one another, you wouldn’t detect photons being exchanged between them at all. Unlike real photons, which carry both energy and momentum, virtual photons exist solely as a calculational tool; there is no “exchange” that’s occurring in any measurable way.
It’s worth pointing out that in the history of the development of quantum field theory, there were a lot of people who easily accepted the calculations that Julian Schwinger was doing, but who rejected Feynman’s calculations and diagrammatic interpretation/visualization because of its lack of mathematical rigor. The objections were numerous and varied. Some objected because these “internal lines” weren’t representative of real interactions. Some objected because the illustrations of “momentum transfer” were misleading and meaningless. Some objected because it wasn’t yet proven that Feynman’s and Schwinger’s methods were different formulations of the same theory that always yielded the same answers.
But despite these objections, Feynman’s methods and diagrams came to be the ones adopted by practically all modern physicists for one simple reason: they were the easiest way to correctly calculate the right observables, including interaction strengths, scattering amplitudes, and interaction cross-sections. What you have to recognize is that the “internal photons” (or any other “exchanged” particles) are not real particles, and they are not transferring momentum from one particle to another. Those wiggly lines aren’t truly representing particles, but are instead representing what’s known as the propagator: a function that gives the correct probability amplitude for interactions to occur, and which is derivable from Feynman’s other great contribution to theoretical physics, the path-integral.
In short: the photon comes in one and only one flavor, the flavor that is a massless electromagnetic wave (or, if you must, wavicle) with oscillating, in-phase electric and magnetic fields. When real photons are created, the energy and momentum (and other properties, like polarization, wavelength, and speed) of those photons can be measured, and our detectors can directly make those key measurements. But when we talk about the photons (or any boson) that mediates the electromagnetic (or any other) interaction, those photons aren’t real in any sense. They can be described as:
- virtual,
- as propagators,
- as “terms” in an infinite series that approximates the true strength of the interaction,
- or as a way of visualizing the nature of the interaction,
but we must be careful to not confuse ourselves by endowing them with properties (like energy and momentum) that only real photons actually possess.
The great complication is that Feynman diagrams are an attempt to put deep physical and mathematical concepts into simple, accessible terms. They’re a successful attempt at this in many regards; the diagrams accomplish everything that physicists need them to accomplish. But they’re often unsuccessful in the same way that treating the fabric of space as a taut bedsheet with bowling balls on it is for explaining general relativity: there are many aspects of this analogy that are fundamentally limiting, and if you follow them too closely, you’re going to wind up with misconceptions instead of a deeper understanding of nature. The “virtual photons” aren’t any different in attractive versus repulsive scenarios; the differences are only to be found when you perform the calculations relevant to your physical system that these Feynman diagrams actually encode.
Send in your Ask Ethan questions to startswithabang at gmail dot com!