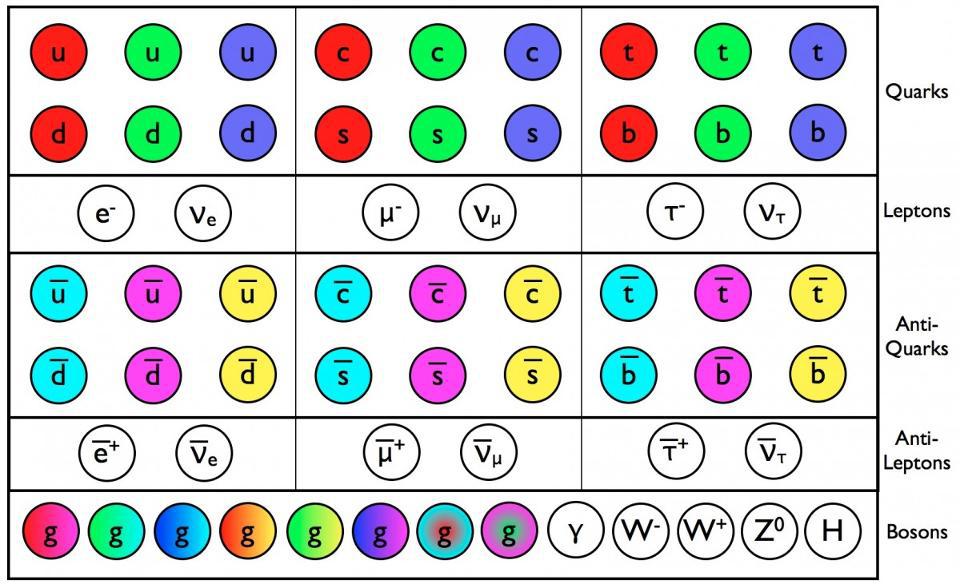
8 basic unanswered questions about the known particles

- With no new particles discovered beyond the Standard Model, despite all of the efforts involved in smashing particles and dark matter direct detection, many are declaring the era of particle physics over.
- But in science, whenever you have puzzles that you can’t explain, you are compelled to search for the answer: even in the most unlikely of places.
- These 8 questions, seemingly simple and basic, remain unanswered even here in 2024. Perhaps discovering the answers will pave the path forward to the next big breakthrough.
There are many aspects of reality that we once assumed we understood, only for it to later be revealed that our earlier understanding was primitive, incomplete, and facile. We thought that nature was purely classical and deterministic, but the wave nature of light, and later the wholehearted discovery of quantum physics, painted a deeper picture of reality. We once thought that atoms made up everything; now we know that atoms are simply one set of examples of how more fundamental particles bind together. Given that we now have the Standard Model of elementary particles, along with the quantum field theories that govern them, it seems foolish to presume that we know all that there is to know about the entities composing our Universe.
While many are on the hunt for new fundamental particles in the quest to solve some of the great mysteries and puzzles of our time, including:
- the dark matter puzzle,
- the matter-antimatter puzzle,
- the dark energy puzzle,
- the hierarchy puzzle,
- and the origin-of-the-Universe puzzle,
the reality is that physics, even ignoring these issues, is still in dire need of rich exploration. In fact, there are a great many unanswered questions about the known particles of the Universe that still remain, even if we ignore all of these vaunted puzzles. Here are eight of the biggest ones, along with a quick look at our prospects for answering them.
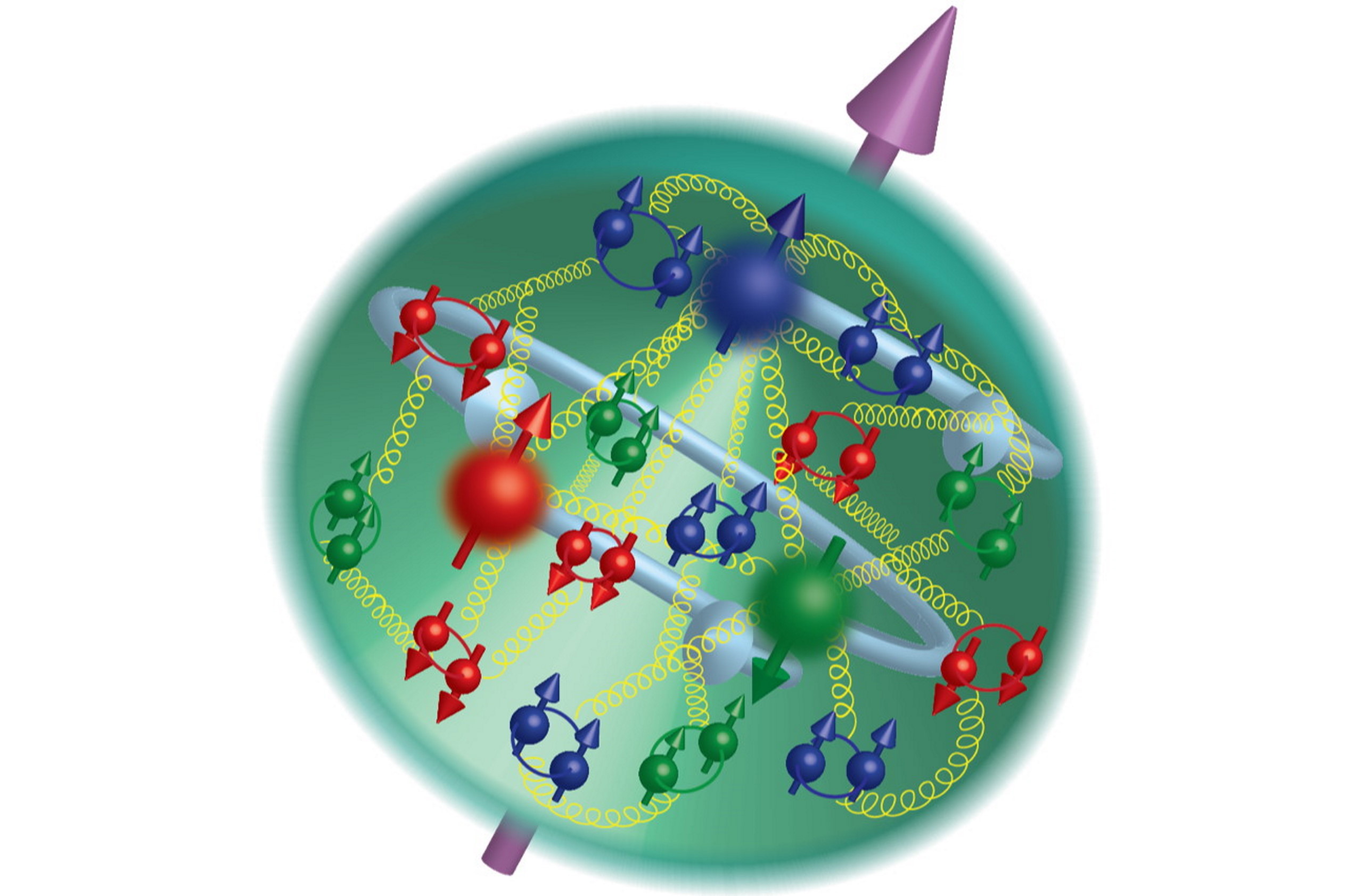
1.) Does the proton decay?
According to the Standard Model, alone, the proton won’t decay. While there are plenty of potential pathways for the proton to decay that conserve energy, momentum, and electric charge, they all violate a key quantum number: baryon number. Protons are the lightest stable baryon (a composite particle made out of three quarks), and are the only baryon that doesn’t have any known decay pathways. Based on enormous experimental setups full of enormous numbers of protons that would be sensitive to even one decaying proton over many years, we can constrain that the lifetime of the proton is at least ~1034 years: around a septillion times the age of the Universe.
And yet, because there must have been a way by which the Universe created or first obtained a matter-antimatter asymmetry, some sort of baryon number-violating interaction must be possible. In the Standard Model, neither baryon number (B) nor lepton number (L) are strictly conserved; only the difference B – L is conserved. If we can push the lifetime of the proton up past ~1038 years or so, we can rule out a large number of grand unified theories; if we find that the proton does decay, we might gain a window into the existential problem of baryogenesis. As we scale up to larger neutrino and dark matter detectors, we can also expect improved constraints on (and a possible discovery of) proton decay.
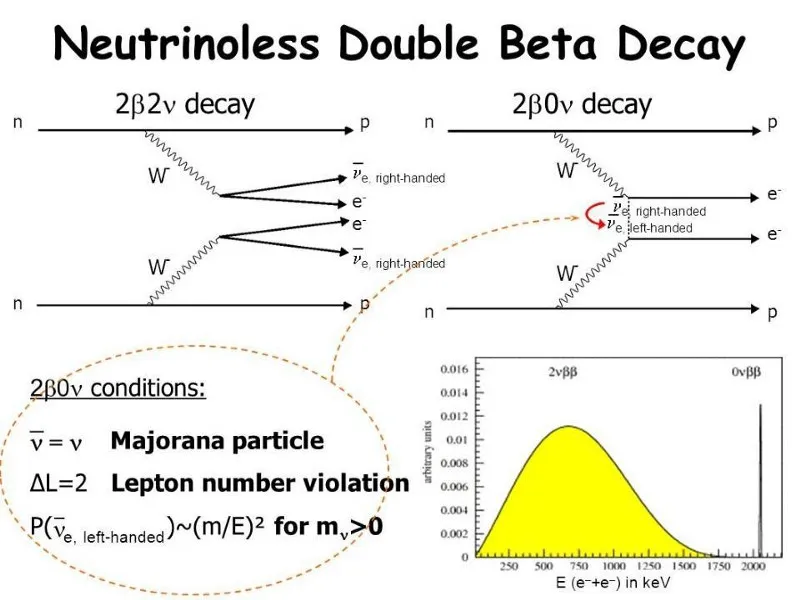
2.) Can neutrinoless double beta decay occur?
Most atomic nuclei contain both protons and neutrons inside them. In these composite configurations, some of them are eternally stable, meaning they’ll never spontaneously decay into components with lower net masses. Inside the unstable ones, however, there are a variety of pathways that can occur to cause the nucleus to decay, including:
- alpha decay (where a helium nucleus is emitted),
- beta decay (where a neutron within the nucleus decays to a proton, an electron, and an electron antineutrino),
- gamma decay (where a photon is emitted),
- and electron capture (where an electron is captured by a proton, converting it to a neutron and an electron neutrino),
among others.
One of those “others” is double beta decay: where two neutrons simultaneously decay into two protons, two electrons, and two electron antineutrinos. Many have recognized that if neutrinos are Majorana particles — i.e., are their own antiparticle — then it should be possible to also have neutrinoless double beta decay: where one emitted electron antineutrino behaves as a neutrino and “cancels out” the other electron antineutrino, resulting in the emission of two protons and two electrons alone. This process has never been observed, but the search for it is ongoing. If we even discovered it, it would point to new neutrino physics that could take us far beyond the Standard Model.
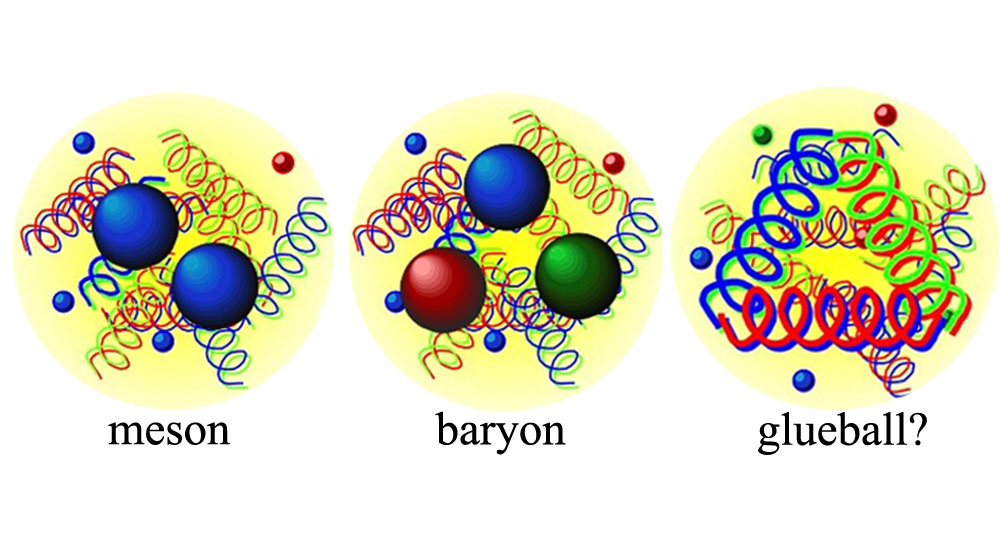
3.) Do glueballs exist?
In terms of particles bound together by the strong nuclear force, the only ones we know of are fundamentally composed of quarks and/or antiquarks.
- Three quarks make a baryon,
- three antiquarks make an antibaryon,
- a quark-antiquark combination makes a meson,
- two quarks and two antiquarks make a tetraquark,
- four quarks and one antiquark (or four antiquarks and one quark) make a pentaquark state,
- six quarks can make a dibaryon state,
and so on. So long as you wind up with a “colorless” state under the rules of quantum chromodynamics and obey the other quantum rules about spin, electric charge, parity, charge conjugation, and more, you can create a bound QCD state.
In theory, this should also be possible without any quarks at all: to have a bound state of (at least two) gluons alone. These hypothetical states, known as glueballs, have been predicted for around 50 years, but none have ever been experimentally revealed before. However, in an exciting development, the X(2370) particle has just been observed to have the same quantum numbers and the predicted mass of the lightest glueball state, making this the first realistic glueball candidate. If there are no glueballs at all, then something is fundamentally wrong with QCD, indicating an interesting test case for the Standard Model either way.

4.) Do any forces unify beyond the electroweak scale?
In nature, at least as we understand it today, there are four fundamental forces. There is:
- the gravitational interaction, governed by Einstein’s general relativity,
- the strong nuclear force, governed by quantum chromodynamics,
- the electromagnetic force, governed by quantum electrodynamics,
- and the weak interaction, whose structure is a little more complicated than just being “its own theory” like the other forces.
In the weak interactions, the only way to change the charge of a particle is through the exchange of a (charged) W-boson, but these interactions only couple to the left-handed polarized fermions, rather than left-and-right-handed ones equally.
The underlying theory that explains why is electroweak theory: the notion that, at energies of around ~100 GeV (the electroweak scale), the electromagnetic and weak interactions unify into a single (electroweak) framework. From one perspective, it means that there were just three fundamental forces early on in the Universe’s history: back when the electroweak symmetry was restored. Does this mean, at even earlier phases in cosmic history (or at still higher energies), the strong force, and possibly even the gravitational force, all unify together? Grand unified theories come along with their own host of ideas and a new set of phenomena and/or particles; if any of these phenomena are detected, it could be huge for what new physics is beyond the Standard Model after all.

5.) How does the electroweak symmetry break?
Whenever you have a symmetry spontaneously break, you get a number of things out. You get a Goldstone boson for each degree of symmetry that breaks as a result, but you also typically wind up with a phase transition: where what was once a (quasi-)equilibrium state is now suddenly far out-of-equilibrium, and so properties must change dramatically to bring things back into balance. We normally think of the electroweak symmetry as depicted above: as a ball that begins on the top of a hill when we’re in the restored-symmetry state, and that ball then rolls down the hill into the valley below when the symmetry breaks.
But that type of phase transition — known as a second-order phase transition — is only one of the two main possibilities. It’s also possible to have a first-order phase transition, where there’s a “divot” somewhere either at or near the top of the hill that serves as a false minimum: a place for the ball to get “caught” before reaching the bottom of the valley. If this occurs, then it has a number of implications, with the three biggest being that:
- there must be at least one additional Higgs boson (or Higgs boson-like) particle with the same quantum numbers,
- that Higgs must mix together with the Standard Model Higgs,
- and that the combined field, which plays a role in symmetry breaking, could create the environment necessary to create the matter-antimatter asymmetry observed in our Universe.
Particle physicists who advocate for building a Higgs factory, such as a muon collider or a hadron-hadron based future circular collider, are specifically seeking to answer this question with such an instrument.
6.) How heavy is each species of neutrino?
Whereas most of particle physics focuses on investigating the heavy, unstable particles that require a high-energy collider to create them — particles like the heavy quarks, the W-and-Z bosons, and the Higgs boson — the low-end of the mass spectrum is also curious: the neutrinos. Originally thought to be massless, we now realize that neutrinos don’t just come in three flavors (electron, muon, and tau), but that the different types of flavors can oscillate into one another. This type of “species change” of particle can only occur if neutrinos have mass, and if the three “flavor eigenstates” of electron, muon, and tau are all combinations of the three “mass eigenstates” that enable the neutrino to have mass at all.
We can perform experiments that are sensitive to interactions with various species of neutrino, and determine what the mass-squared difference is between (two of) the different mass eigenstates from both solar neutrino and atmospheric neutrino experiments. We can also perform cosmological experiments that give us upper limits on what the sum of all the neutrino masses must be. However, this isn’t enough information to determine what the actual energy-equivalent values of the mass eigenstates are, or what a neutrino would “read” if you could put it on a scale. Direct neutron decay experiments (from tritium, for example) and cosmological measurements designed to reveal the sum of all three neutrino masses, along with laboratory efforts like the under-construction DUNE, seek to make critical measurements that can help answer this question.

7.) Can any Standard Model particles be “cracked open?”
Sure, we’ve discovered all the particles and antiparticles theorized to be present in the Standard Model. This includes:
- all six species of quark and antiquark,
- the three charged leptons and antileptons,
- the three neutrino and antineutrino species,
- the gluons,
- the photon,
- the W-and-Z boson,
- and the Higgs boson.
We’ve measured properties like their mass, their electric charge, their parity, spin, and much more, and we’ve also seen how they bind together and/or decay in a variety of ways to produce signals that are directly observable in particle detectors.
But what we haven’t established is that each of these particles are truly fundamental: that they themselves aren’t further composed of smaller constituent particles, bound together to produce the particle spectrum we’ve seen directly. It’s possible that the Higgs is a composite particle (in the case of technicolor theory), that quarks are composite, that leptons and quarks are both composite, or that gauge bosons are composite in nature. This one is very challenging to speak authoritatively on, as particles can only be tested for compositeness up to the energy scale of the collisions used to probe them. Up above the energy scale of the LHC, we simply do not have an answer for these questions.

8.) Are inertial and gravitational mass always equal?
Place a massive particle in proximity to any other source of mass, and it will respond in exactly the fashion you expect: by experiencing gravitational attraction. The amount that the particle accelerates by, in a gravitational field, is directly related to that particle’s gravitational mass. Spacetime curves (in general relativity) in proportion to that particle’s mass-and-energy, which also relates to gravitational mass.
On the other hand, whenever you create a particle, it takes a certain amount of energy to create it, an energy that’s quantifiable via E = mc². When you apply a force to that massive particle, via Newton’s F = ma, for example, it accelerates by an amount that we can determine by dividing the applied force by its mass. In this case, that’s known as inertial mass: the mass that’s related to the rest-energy of the particle in question.
Now, here’s a question: are inertial and gravitational mass exactly identical to one another?
To the limits of the experiments we can perform, including on Earth and in space, the answer seems to be yes: to about 1-part-in-1012 under laboratory conditions for conventional, atom-based matter. Experiments performed in the early 20th century helped Einstein formulate his equivalence principle, which led to general relativity and is a foundational principle in physics. But there are further tests to perform: to greater precision, for exotic particles, and under a variety of conditions. We are not certain these two quantities are always equivalent.

It’s easy to speculate about what lies out there beyond the limits of what is known. In some cases, we have areas that we know we need to learn more about, like dark matter, dark energy, cosmic inflation, and the matter-antimatter asymmetry. These are phenomena whose existence has many mountains of evidence backing them up, but we remain ignorant about many of the specifics of each of them. But what we mustn’t overlook are important questions that we have expectations for how they’ll turn out, but where there remains so much more to learn and investigate before we can give definitive answers.
We assume that the matter in the Universe is fundamentally stable, but if the proton decays, it may not be. We assume that all neutrinos are left-handed and all antineutrinos are right-handed, but if neutrinos are Majorana particles, we can turn matter into antimatter (and vice versa) simply by changing our motion. And we assume that neutrinos are low in mass and there is a significant hierarchy between masses of different species of neutrino, but nature could still surprise us on this front. Before we’re ready to leave the Standard Model behind, there are important questions about it that are still awaiting definitive answers. It would be folly to assume we know the answers without first making the critical measurements needed to experimentally determine them.