How the “Einstein shift” was predicted 8 years before General Relativity

- One of the novel predictions that came along with Einstein’s novel theory of gravity was the idea of “the Einstein shift,” or as it’s known today, a gravitational redshift.
- But even though it wouldn’t be experimentally confirmed until a 1959 experiment, Einstein himself recognized it was an absolute necessity way back in 1907: a full 8 years before General Relativity was completed.
- Here’s the remarkable story of how, if you yourself had the same realizations that Einstein did more than 100 years ago, you could have predicted it too, even before General Relativity.
It’s extremely rare for any individual to bring about a scientific revolution through their work: where practically everyone conceived of the Universe in one way before that critical work was completed, and then afterward, our conception of the Universe was entirely different. In the case of Albert Einstein, this happened not just once, but multiple times. In 1905, Einstein brought us:
- the constancy of the speed of light,
- mass-energy equivalence (via E = mc²),
- and the special theory of relativity,
among other important advances. But arguably, Einstein’s biggest revolution came a decade later, in 1915, when he incorporated gravitation into relativity as well, leading to the general theory of relativity, or General Relativity, as it’s more commonly known.
With spacetime now understood as a dynamic entity, whose very fabric is curved by the presence and distribution of matter-and-energy, all sorts of new phenomena have been derived. Gravitational waves — ripples that travel through spacetime, carrying energy and moving at the speed of light — were predicted. The bending of starlight around massive, compact objects was an inevitable consequence, as were other gravitational effects like gravitational time dilation and additional orbital precessions.
But the first expected consequence ever predicted from General Relativity — the Einstein shift, also known as gravitational redshift — was predicted way back in 1907, by Einstein himself. Here’s not just how he did it, but how anyone with the same realization, including you, could have done it for themselves.

Imagine you have a photon — a single quantum of light — that’s propagating through space. Light isn’t just a quantum mechanical “energy packet,” but is also an electromagnetic wave. Each photon, or each electromagnetic wave, has a certain amount of energy inherent to it, and the precise amount of energy it possesses is related to its wavelength. Photons with shorter wavelengths have higher energies, with gamma rays, X-rays, and ultraviolet light all more energetic than visible light. Conversely, photons with longer wavelengths have lower amounts of energy inherent to them, with infrared, microwave, and radio waves all less energetic than visible light.
Now, we’ve known for a long time that other types of waves, like sound waves, will appear to be “shortened” or “lengthened” relative to the wavelength at which they were emitted dependent on the relative motions of the source and the observer. It’s the reason why an emergency vehicle’s siren (or an ice cream truck) sounds higher-pitched when it moves toward you, and then lower-pitched when it moves away from you: it’s an example of the Doppler shift.
And if light is a wave in precisely the same fashion, then the Doppler shift, once special relativity came along in 1905, must also apply to light.
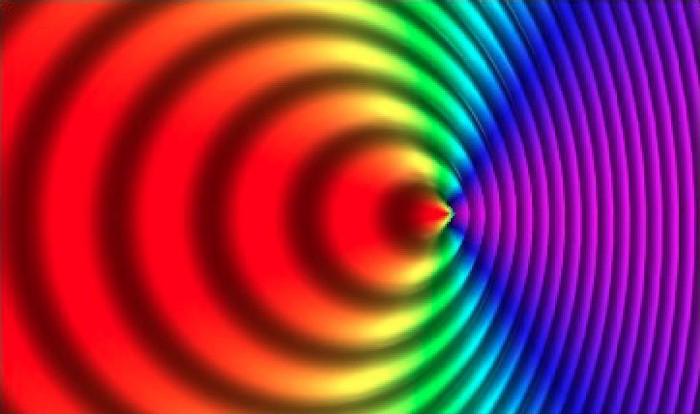
Light can have its wavelength either stretched or compressed due to relative motion, in a Doppler redshift or a Doppler blueshift, but that’s hardly revolutionary or even unexpected. However, it was two years after special relativity, in 1907, that Einstein had what he’d later refer to as his happiest thought: the equivalence principle.
The equivalence principle, in its most straightforward form, simply states that there is nothing special or remarkable about gravitation at all; it’s simply another example of acceleration. If you were being accelerated, and you had no way of observing the source of your acceleration, could you tell the difference between whether propulsion, an external applied force, or a gravitational force was the cause of it.
With this realization — that gravitation was just another form of acceleration — Einstein recognized that it would be possible to make a more general theory of relativity that didn’t just incorporate all possible motions and changes in motions, but one that also included gravitation. Eight years later, his happiest thought would lead to General Relativity and a wholly new conception of how gravity worked.

But we wouldn’t have to wait until 1915 for the Einstein shift — what we now know as gravitational redshift (or gravitational blueshift) — to arise as a robust prediction. In fact, it was way back in 1907, when he first thought of the equivalence principle, that Einstein published his first prediction of this new type of redshift.
If you were in a spacecraft (or an elevator) that was accelerating upward, then a photon that was emitted from “beneath” you would have its wavelength stretched relative to its emitted wavelength by the time the photon caught up to your eyes. Similarly, if an identical photon were emitted from “above” you instead, its wavelength would appear compressed relative to the wavelength at which it was emitted. In the former case, you’d observe a Doppler redshift; in the latter, a Doppler blueshift.
By applying the equivalence principle, Einstein immediately recognized that the same shifts must apply if the acceleration were due to a gravitational field rather than a moving-and-accelerating spacecraft. If you’re seeing a photon rising up against a gravitational field, you’ll observe it to have a longer wavelength than when it was emitted, a gravitational redshift, and if you’re seeing a photon falling down into a gravitational field, you’ll observe that it has a shorter wavelength, or a gravitational blueshift.

Once Einstein developed both the equivalence principle and what would become his general theory of relativity more comprehensively, in 1911, he quantitatively was able to predict the gravitational redshift of a photon rising out of the gravitational field of the Sun: a prediction that wouldn’t be verified until 1962: seven years after his death. The only robust astronomical observation that ever confirmed gravitational redshift during Einstein’s lifetime came in 1954, when astronomer Daniel Popper measured a gravitational redshift for the spectral lines coming from the white dwarf 40 Eridani B, and found a strong agreement with the predictions of General Relativity.
There was a direct laboratory experiment in 1959, however, that provided our best confirmation of gravitational redshift: the Pound-Rebka experiment. By causing a particular isotope of iron to enter an excited nuclear state, that nucleus would then emit a gamma-ray photon of a specific wavelength. When sent upward, 22.5 meters, to an identical iron nucleus, the gravitational redshift changed that photon’s wavelength significantly enough that the higher nucleus couldn’t absorb it. Only if the nucleus was “driven” with an additional velocity — i.e., if it received an energetic “kick” — would there be enough extra energy in the photon that it would get absorbed again. When the calculation was performed to show how much energy must be added versus how much did General Relativity predict would be needed, the agreement was astounding: to within 1%.

Not everyone anticipated that this would be the case, however. Some thought that light wouldn’t respond to moving deeper into (or out of) a gravitational field by gaining (or losing) energy, as the equivalence principle demanded. After all, the equivalence principle’s main assertion was that objects that are accelerated by a gravitational force cannot be distinguished from objects that are accelerated by any other type of force: i.e., an inertial force. The tests we were able to perform of the equivalence principle, especially early on, only tested the equivalence of gravitational masses and inertial masses. Massless particles, like photons, had no such test for equivalence.
However, once the world knew about the existence of antimatter — which was indisputable by the early 1930s, both theoretically and experimentally — there was a simple thought experiment that one could have performed to show that it couldn’t be any other way. Matter and antimatter particles are the same in one way, as they have identical rest masses and, therefore (via E = mc²) identical rest mass energies. However, they have opposite electric charges (as well as other quantum numbers) from one another, and most spectacularly, if you collide a matter particle with its antimatter counterpart, they simply annihilate away into two photons of identical energy.

So, let’s imagine that this is precisely what we have: two particles, one matter and one antimatter. Only, instead of having them here on the surface of Earth, we have them high up above the Earth’s surface: with lots of gravitational potential energy. If we hold that particle-antiparticle pair at rest and simply allow them to annihilate with one another, then the energy of each of the two photons produced will be given by the rest mass energy inherent to each member of the particle-antiparticle pairs: E = mc². We’ll get two photons, and those photons will have well-defined energies.
But now, I’m going to set up two different scenarios for you, and you’re going to have to think about whether these two scenarios are permitted to have different outcomes or not.
- The particle-antiparticle pair annihilates up high in the gravitational field, producing two photons that eventually fall down, under the influence of gravity, to the surface of the Earth. Once there, we measure their combined energies.
- The particle-antiparticle pair are dropped from up high in the gravitational field, where they fall downward under the influence of gravity. Just before they hit the Earth’s surface, we allow them to annihilate, and then we measure their combined energies.
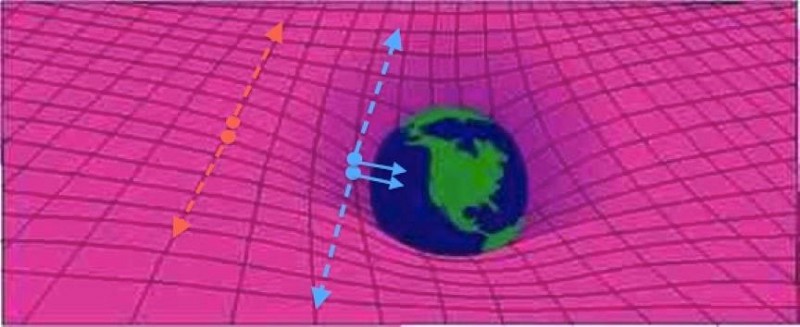
Let’s think about what’s happening in the second situation first. As the two masses fall in a gravitational field, they pick up speed, and therefore gain kinetic energy. When they’re just about to reach the surface of the Earth and they annihilate, they will produce two photons.
Now, what will the energy, combined, of those two photons be?
Because energy is conserved, both the rest mass energy and the kinetic energy of that particle-antiparticle pair must go into the energy of those two photons. The total energy of the two photons will be given by the sum of the rest mass energies and the kinetic energies of the particle and the antiparticle.
It couldn’t be any other way, because energy must be conserved and there are no additional places for that energy to hide.

Now, let’s go back to the first situation: where the particle-antiparticle pair annihilates into two photons, and then the two photons fall deeper into the gravitational field until they reach the surface of the Earth.
Let’s once again consider, at the moment those two photons reach the surface of the Earth, what with their combined energy be?
Can you see, immediately, that a difference between these two situations isn’t allowed? If energy is conserved, then it cannot matter whether your matter antimatter pair:
- first annihilates into photons, and then those photons fall down deeper into a gravitational field, or
- falls down deeper into the gravitational field, and then that pair annihilates into photons.
If the starting conditions of both scenarios are identical, if there are no processes that occur in one scenario that don’t also occur in the other, and if the two photons wind up in the same (or equivalent) state at the end of both scenarios, then they must also have identical energies. The only way for that to be true is if photons, when they fall deeper into a gravitational field, experience the Einstein shift due to gravitation: in this case, a gravitational blueshift.
In many ways, this thought experiment illustrates perhaps the greatest difference between the older, Newtonian conception of gravitation and the modern one, General Relativity, given to us by Albert Einstein. In Newtonian gravity, it’s only an object’s rest mass that leads to gravitation. The force of gravity is determined by each of the two masses that are exerting the force on one another, as well as the distance (squared) between them. But in General Relativity, all forms of energy matter for gravitation, and all objects — even massless ones — are subject to gravity’s effects.
Since photons carry energy, a photon falling deeper into a gravitational field must gain energy, and a photon climbing out of a gravitational field must lose energy in order to escape. While massive particles would gain or lose speed, a photon cannot; it must always move at the universal speed for all massless particles, the speed of light. As a result, the only way photons can gain or lose energy is by changing their wavelength: blueshifting as they gain energy, redshifting as they lose it.
If energy is to be conserved, then photons must experience not just Doppler shifts due to the relative motion between an emitting source and the observer, but they’ll experience gravitational redshift and blueshifts — the Einstein shift — as well. Although it took approximately half-a-century to validate it observationally and experimentally, from a purely theoretical perspective, it never could have been any other way.