Time dilation is real, and your head ages faster than your feet

There’s no such thing as absolute time. No matter where you are, how fast you’re moving, or how strong the gravitational field is around you, any clock you have on you will always record time as passing at the same rate: one second per second. For any solitary observer, time simply flows.

But if you have two different clocks, you can compare how time flows under different conditions. If one clock remains stationary while the other travels quickly, the fast-moving clock will experience a smaller amount of time passing than the stationary clock: that’s the rule of time dilation in special relativity.

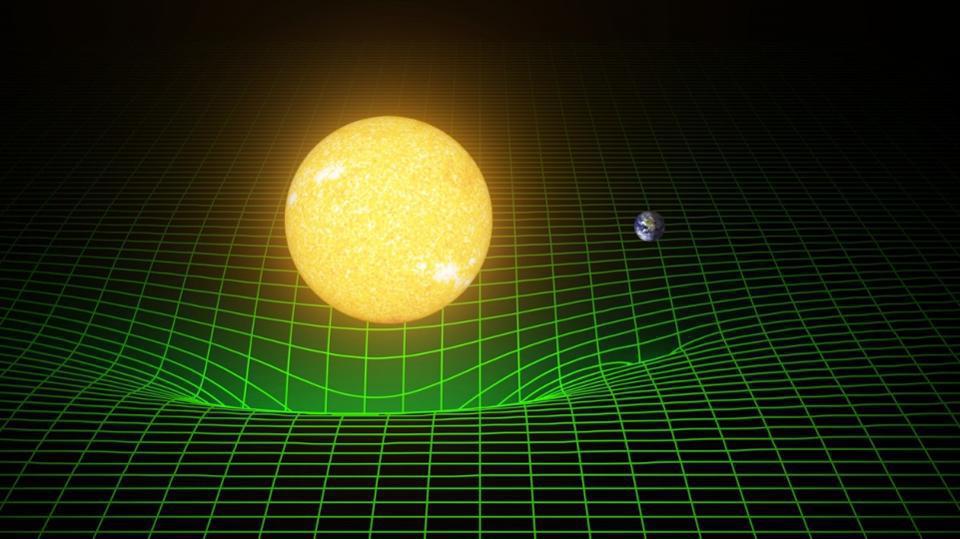
What’s even more counterintuitive, however, is that the relative flow of time also depends on the difference between how severely space is curved between two locations. In General Relativity, this corresponds to the strength of gravity at your particular location, which means that your feet actually age at a different rate than your head when you’re standing up. Here’s the physics of how we know.

Electron transitions in the hydrogen atom, along with the wavelengths of the resultant photons, showcase the effect of binding energy and the relationship between the electron and the proton in quantum physics. The Bohr model of the atom provides the coarse (or rough, or gross) structure of these energy levels. Hydrogen’s brightest atomic transition is Lyman-alpha (n=2 to n=1), but its second brightest is visible: Balmer-alpha (n=3 to n=2), which emits visible (red) light at a wavelength of 656 nanometers. The energy lost by an electron cascading down the energy levels gets emitted in the form of photons.

One of the things we rely on is that the laws of physics are universal. While the properties of the Universe might change with time, with energy, or with your location, the rules and the fundamental constants that govern it remain the same. A hydrogen atom located anywhere in the Universe will always have electron transitions occurring at the same energies, and the quanta of light they emit will be indistinguishable from any other hydrogen atom in the Universe.

The same thing is true for ionic, molecular, or even nuclear transitions: the laws of physics remain the same at all times and all places, and so these transitions that emit or absorb photons always occur at the same energy. However, if the emitter of a photon and the (potential) absorber of a photon aren’t located at the same time and place as one another, there’s a good chance that they won’t agree on the energies they observe.

An object moving close to the speed of light that emits light will have the light that it emits appear shifted dependent on the location of an observer. Someone on the left will see the source moving away from it, and hence the light will be redshifted; someone to the right of the source will see it blueshifted, or shifted to higher frequencies, as the source moves toward it.

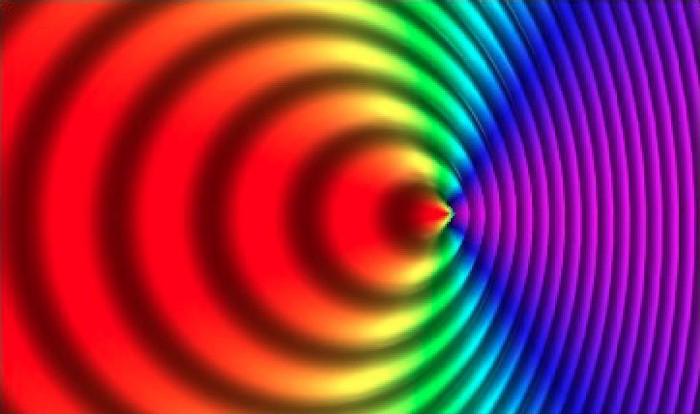
When it’s because the objects are in relative motion with respect to one another, we know this effect as a Doppler shift. Most of us experience the Doppler shift every time we hear an emergency vehicle (or an ice cream truck) either approaching us or moving away from us: we can hear the pitch of the siren change. If the vehicle is approaching you, its waves will appear to be shifted closer together, and you’ll hear a higher pitch; if it’s moving away from you, its waves will be shifted to arrive spaced farther apart, and you hear a lower pitch.

For light, it’s a practically identical scenario: if the source and observer are moving away from one another, the light gets shifted toward longer (redder) wavelengths, while if they’re moving toward one another, the light gets shifted toward shorter (bluer) wavelengths.

Now, here’s where things get weird: this same type of shift should also occur — even if everyone is stationary — when your gravitational field strength changes from one location to another.

When a quantum of radiation leaves a gravitational field, its frequency must be redshifted to conserve energy; when it falls in, it must be blueshifted. Only if gravitation itself is linked to not only mass but energy, too, does this make sense. Gravitational redshift is one of the core predictions of Einstein’s general relativity, but has only recently been tested directly in such a strong-field environment as our galactic center.

Just as you can have Doppler redshifts and blueshifts for light, you can also have gravitational redshifts and blueshifts. For example, if you send a photon from the Sun to the Earth, because the Sun’s gravitational field dominates the Solar System and is stronger near the Sun than farther away, that photon will lose energy (and become “redder”) as it travels from the Sun to the Earth. If it were to go in the opposite direction, from the Earth to the Sun, the photon would gain energy and become “bluer” in color.

There were a lot of doubters in the physics community who thought that this idea — of a gravitational redshift — was completely unphysical. It’s intricately related to the rate at which clocks run: the number of wave “crests” that pass by your location over any time interval determine the frequency of the light you receive, and if gravitational redshifts are real, then sending a photon higher or lower in a gravitational field should lead to observable consequences. That means, as is the case for most physics predictions, there’s a way to test it.

The atomic transition from the 6S orbital in a cesium-133 atom, Delta_f1, is the transition that defines the meter, second, and the speed of light. Slight changes in the observed frequency of this light will occur based on motion and the properties of spatial curvature between any two locations. Spin-orbit interactions, as well as various quantum rules and the application of an external magnetic field, can cause additional splitting at narrow intervals in these energy levels: examples of fine and hyperfine structure.

Let’s say you induce a quantum transition. Either an electron shifts in energy levels or an excited nucleus reconfigures itself, releasing an energetic photon. If you have a similar atom (or atomic nucleus) nearby, it should be able to absorb that photon, as the same physics that results in the emission of a photon can also lead to the reverse process: the absorption of that photon.

If, however, you shift the photon to either longer or shorter wavelengths — regardless of how you do it — you won’t be able to absorb it anymore. The laws of the quantum Universe are pretty rigid, and if a photon comes in with slightly too much or too little energy, it won’t trigger the proper excitation.

This led to a remarkable experiment, the Pound-Rebka experiment, which sought to demonstrate and quantify the existence of gravitational redshift, and to prove that time really does run faster at your head than at your feet.

Physicist Glen Rebka, at the lower end of the Jefferson Towers, Harvard University, calling Professor Pound on the phone during setup of the famed Pound-Rebka experiment. A photon emitted from the bottom of the tower would not be absorbed by the same material at the top without further modifications: evidence of gravitational redshift. When a speaker “kicked” the emitting photon with additional energy, the atoms at the top of the tower could suddenly absorb those emitted photons, strengthening the case for our understanding of gravitational redshift as predicted by general relativity.

The experimenters set up a photon-emitting source within a vertical tower, and then put that same material at the other end of the tower. If there were no gravitational redshift — i.e., if time ran at the same rate for everyone — then the material at the other end of the tower should absorb the photons emitted from the first end.

They didn’t, of course, because they had the wrong energy, and hence, the wrong wavelength.

But what Pound and Rebka did was set up an oscillator (basically the interior of a speaker) that allowed them to “boost” the photon-emitting material at one end of the tower. If they boosted it by just the right amount, they reasoned, they could tune this induced Doppler shift to exactly cancel out the predicted gravitational redshift. As far as time goes, it basically added an extra motion (and an extra bit of time dilation) to compensate for the effects that gravity introduces.

A photon source, like a radioactive atom, will have a chance of being absorbed by the same material if the wavelength of the photon doesn’t change from its source to its destination. If you cause the photon to travel up or down in a gravitational field, you have to change the relative speeds of the source and receiver (such as driving it with a speaker cone) in order to compensate. This was the setup of the Pound-Rebka experiment from 1959.

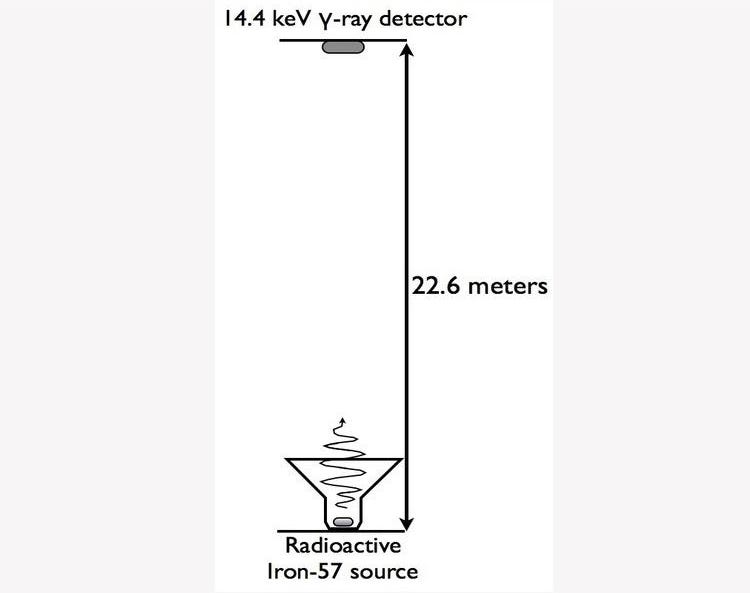
All of a sudden, when the right frequencies were reached, the (iron) atoms began absorbing those emitted photons from the other end. The initial experiment confirmed General Relativity’s predictions, and was subsequently improved upon by Pound and Snider throughout the 1960s.

The overall lesson is this: for every meter of height that you gain, you need a Doppler shift of ~33 nanometers-per-second to compensate for it. It’s like being lower on the surface of the Earth requires you to be in motion at a certain rate just to have time pass at the same rate as it would if you were higher. In other words, without an extra little speed boost at your feet — without an extra amount of time dilation added in — time passes more quickly at higher elevations in Earth’s gravitational field.

Your head, to be blunt, ages more quickly than your feet do.

Although we don’t think about it very often, the people who have their heads farther from the center of the Earth are experiencing time passing at a slightly different rate from the people whose heads are closer to Earth’s center. This is a consequence of gravitational time dilation, and it applies to physicists (like George Gamow, with pipe) and non-physicists equally.

But you can do even better than those original experiments: by measuring the passage of time directly using atomic clock technology. The way we define time has evolved over the centuries; what used to depend on the motion of the Earth rotating on its axis or revolving around the Sun has now been replaced by an atomic definition. A second, as we know it, is defined by the cesium-133 atom.

In that atom, there’s a hyperfine transition that’s incredibly precise, emitting a photon of a very particular wavelength. That wave, if you take 9,192,631,770 cycles of it, is our modern definition of the second.

And yet, if you took an atomic clock — whether based on cesium, mercury, aluminum, or any other element — and moved it to a different elevation, that clock would run at a different rate from its original elevation: faster at higher elevations (in a weaker gravitational field), slower at lower elevations (in stronger gravitational fields).

A difference in the height of two atomic clocks of even ~1 foot (33 cm) can lead to a measurable difference in the speed at which those clocks run. This allows us to measure not only the strength of the gravitational field, but the gradient of the field as a function of altitude/elevation. Atomic clocks, which rely on electron transitions in atoms, are the most precise devices for measuring time presently accessible to humans.

This has been experimentally verified to astonishing precision, as we’ve detected these predicted shifts for height differences as small as 0.33 meters (1 foot). In Earth’s relatively weak gravitational field, this is a remarkable achievement, demonstrating just how accurate timekeeping with atomic clocks has become.

But if we took this to a more extreme environment, the effects would become enormous. No environment in the Universe is more gravitationally extreme than a black hole. If you approached its event horizon, time would pass so slowly for you that, in a single second (for you), centuries, millennia, or even eons could pass for someone far away.

It’s enough to make one worry that even if we could successfully build a wormhole, the intense curvature of space could cause the entire meaningful part of the Universe — where we have stars, galaxies, and interesting chemistry occurring — to pass by while the traveler passed through it.

Traveling through a wormhole is a fascinating proposition, but there are many barriers to creating one in our actual Universe. Unless exotic matter, negative energy, extra dimensions, or some similarly fanciful entities exist, even non-traversable wormholes are forbidden. If traversable wormholes can exist, effects like time dilation and extreme tidal forces must still be reckoned with to avoid destroying the matter inside.

In our Universe, time will pass the fastest for the observer who minimizes their motion through space and is located where the curvature of space is as little as possible. If you could travel to the space between galaxies, where you’re far away from any sources of mass, you would age more quickly than anyone else. Here on Earth, the farther you are from the center, the faster time runs for you. The effects are extremely slight, but measurable, quantifiable, and robust.

This means, if you ever wanted to time travel to the future, your best bet might not be to take a long, round-trip journey at nearly the speed of light, but rather to hang out where there’s a lot of spatial curvature: near a black hole or neutron star, for instance. The deeper into a gravitational field you go, the slower time will run for you compared to those who are farther out. It might only grant you a few extra nanoseconds over your entire life, but standing up — and keeping your head farther from Earth’s center — really will give you a little bit more time than laying down.