Ask Ethan: How did matter come to exist in our Universe?
- In all the particle physics reactions we've ever created, measured, or observed here on Earth, matter and antimatter can only ever be created or destroyed in equal amounts.
- But somehow, what emerged from the ashes of the hot Big Bang led to a matter-dominated Universe, with scarcely any antimatter around at all.
- This is one of the greatest mysteries in physics: the puzzle of why we live in a matter-dominated Universe, also known as the baryogenesis puzzle. Here's what science knows about it today.
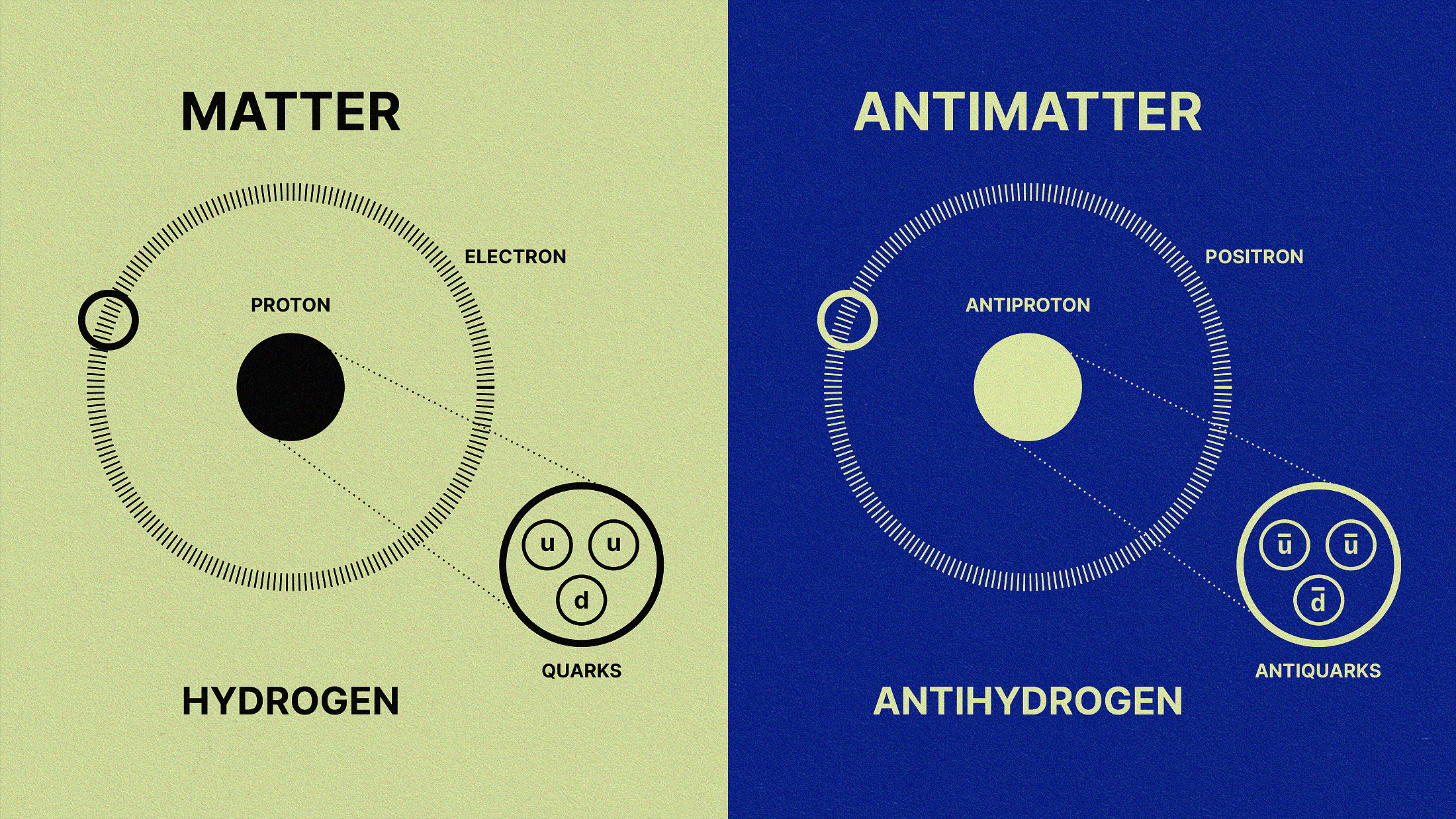
Everywhere we look in the Universe, we find structure of some sort: planets, stars, gas, dust, plasma, and galaxies galore. Every indication we have is that each one of those structures we see is overwhelmingly composed of normal matter, like quarks and leptons, with only trace amounts of antimatter, made of things like antiquarks and antileptons. And yet, when we perform our particle experiments here on Earth, at low energies and at high energies, using particles from colliders as well as particles from cosmic rays, we always find the same thing: that our reactions, while they can create and destroy matter, can only do so at the expense of creating and destroying an equivalent amount of antimatter.
So how, then, did all the matter, and not an equal amount of antimatter, come to exist in our Universe? That’s the topic of this week’s Ask Ethan question thanks to Mateen Khan, who writes in wanting to know:
“Can you help me understand how matter came to existence from almost nothing (at the moment of big bang) to its vast abundance everywhere in the universe and still growing. I am puzzled with the fact that matter is not a living organism, so how come it has multiplied in a sense to keep growing?”
Although it isn’t quite the case that the matter abundance is growing or multiplying with time, it is true that our Universe must have generated a matter-antimatter asymmetry, somehow, in the distant past. Here’s what science knows about that puzzle as of today.

To start thinking about how matter came into existence, you have to understand that “almost nothing” is not a good description of what the Universe was like at the start of the hot Big Bang. In fact, it was likely just the opposite, as “almost everything,” at least in terms of what is allowed by the incredibly high energies and temperatures present at the start of the hot Big Bang, is what we fully expect existed. As the hot Big Bang began, the Universe was:
- incredibly dense,
- incredibly hot and energetic,
- filled with matter, antimatter, and radiation,
- and was also expanding and cooling incredibly rapidly.
The temperatures were at least as high as the hottest temperatures ever reached at particle colliders such as the Large Hadron Collider at CERN, but were likely far hotter: perhaps as much as a factor of 100 billion times hotter!
Under those energetic conditions, anytime two quanta (i.e., particles of any type or species) collide or interact with one another, they have the potential to produce new quanta, including particle-antiparticle pairs. Remember, Einstein’s famous equation, E = mc², tells us that if you have enough available energy, you can create any quantum particle or antiparticle with even a high mass.

At the energies achieved in the early stages of the hot Big Bang, this wouldn’t just create copious amounts of every known particle (and antiparticle) present in the Standard Model, but perhaps yet-unknown species of particles (and antiparticles) that have never been observed or detected by humanity: at energies we have yet to achieve. Although we know so much about the Universe, we know we don’t know everything, as the Standard Model, on its own, cannot account for much of what we observe, including:
- dark matter,
- dark energy,
- the non-zero but tiny masses of neutrinos,
- the lack of observed CP violation in the strong force,
- the values of the masses of the fundamental particles and why they’re so low compared to the Planck mass,
- and how the Universe came to be dominated by matter-over-antimatter.
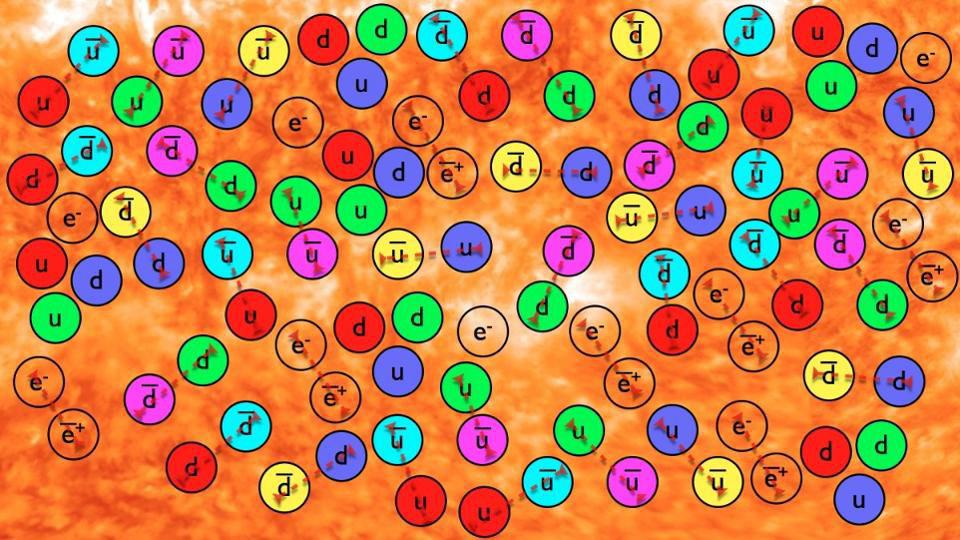
Some of the greatest speculative ideas in theoretical physics come from considering these puzzles, including ideas like grand unified theories, the axion particle, supersymmetry, and extra dimensions. Perhaps the solution to some, or perhaps even all, of these puzzles lies in understanding what occurs at these very high energies in the early Universe? That’s a reasonable suggestion, since we have every reason to believe that the Universe was born with equal amounts of particles and antiparticles at the start of the hot Big Bang, and yet has been matter-antimatter asymmetric since before the formation of protons and neutrons, which happened just microseconds after the Big Bang occurred.
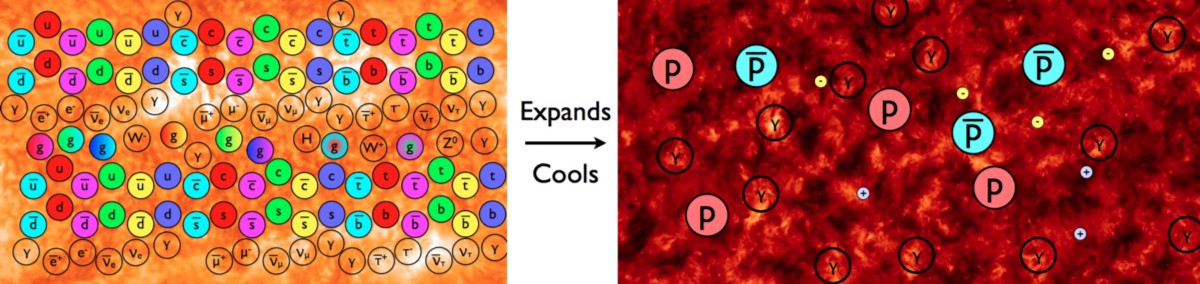
This is a puzzle. If every reaction that we know of creates or destroys particles and antiparticles in equal numbers, and there are conservation laws we have to obey, then even with enough energy and Einstein’s E = mc² at our disposal, we should only be able to bring matter particles into existence by creating an equal number of antimatter particles. And then, when the Universe cools so that the excess matter and antimatter particles annihilate away, we should go back to zero (or an extremely small amount that’s equal parts matter and antimatter) instead of the state we observe: where matter dominates over antimatter.
This matter-dominance is interesting. When protons and antiprotons, or neutrons and antineutrons, or electrons and positrons annihilate, they typically wind up producing photons: quanta of light. And there are plenty of photons left over from the Big Bang, as that’s what the modern cosmic microwave background (CMB) is made out of: 411 of them per cubic centimeter of space, as measured. We can compare that photon density, the number of protons, neutrons, and electrons that are present in the Universe today, and find out what the baryon (protons + neutrons) to photon ratio is, and we find that there’s one baryon for every approximately 1.6 billion photons in the Universe. There’s an electron for every proton to keep the Universe neutral, but no counterbalancing amount of antimatter for all the matter we have.
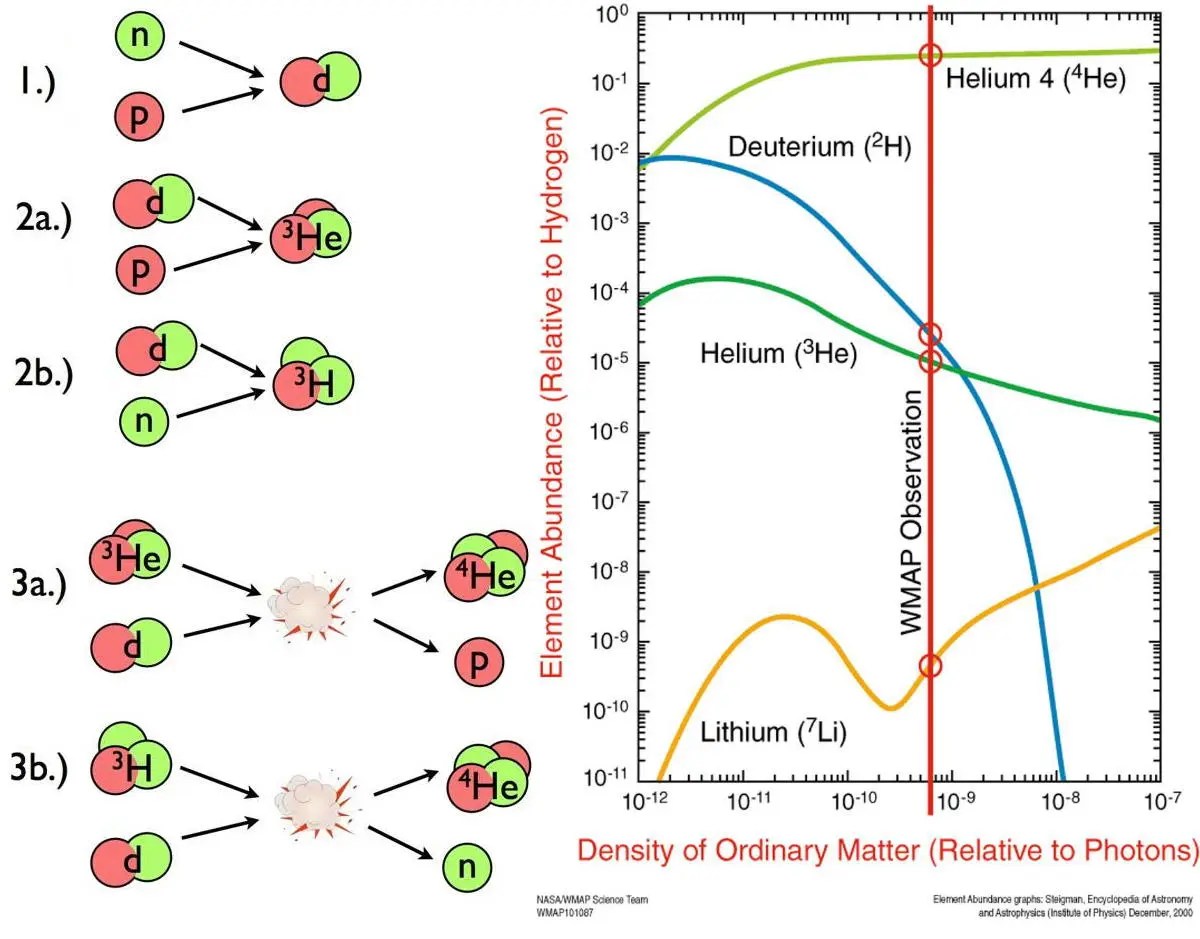
Somehow, we had to take a state that was symmetric, at very high energies and early times, between matter and antimatter, and wind up with a state that was very asymmetric at lower energies and later times. Somehow, within that first tiny fraction-of-a-second after the start of the hot Big Bang, something we do not fully understand occurred to create an asymmetry between matter and antimatter, where none existed previously, so that just a few microseconds later, there was around one extra matter particle for every billion matter-and-antimatter pairs that existed.
But how?
Believe it or not, the general conditions for this to occur were derived all the way back in 1967 by physicist Andrei Sakharov, and there are only three things (known as Sakharov conditions) that must be true to generate a matter imbalance in the Universe.
- You need for out-of-equilibrium conditions to exist.
- You need for both C-violation and CP-violation in your interactions and decays.
- And you also need for interactions that violate baryon number to exist.
Let’s unpack what each of these means.

Conditions are in equilibrium when quanta in your system can collide and interact and exchange information with one another on timescales that are short compared to the timescales over which your system evolves. A solid, stable room where all of the gas particles within it come to the same temperature is an example of a system in equilibrium. However, if you rapidly change the environment by expanding or contracting the room, your system can go out-of-equilibrium. The expanding-and-cooling Universe, quite possibly, is the ultimate out-of-equilibrium system, fulfilling the first Sakharov condition easily.
Two of the more important symmetries to consider in physics are known as charge conjugation (C) symmetry and parity (P) symmetry. Charge conjugation involves replacing all the matter particles in your system with antimatter particles (and vice versa), and your system obeys C-symmetry if both systems behave identically, or is C-violating if the systems behave differently. Parity involves reflecting your system in the mirror and seeing if it behaves the same or differently: P-symmetric if it behaves the same, but P-violating if it behaves differently. The combination of CP-symmetry involves doing both: replacing your matter particles with antimatter particles (and vice versa) while considering the mirror-reflection behavior of the “replaced” system. Again, if the behavior is identical, your system is CP-symmetric, and if not, it’s CP-violating.

What’s interesting is that C-symmetry, P-symmetry, and the combination of CP-symmetry are all known to be violated in nature, but only by one of the four fundamental forces: the weak interaction. For the strong nuclear force, the electromagnetic force, and the gravitational force, all of the interactions that occur are completely symmetric whether you:
- deal with particles or antiparticles,
- deal with the actual Universe or its mirror reflection,
- and whether you run the clock forward or backward (the third fundamental symmetry, T-symmetry),
or any combination of those three. Only in the weak interactions are the three of C, P, and T-symmetries violated, individually as well as any combination of the two: CP, CT, and PT.
And finally, that third Sakharov condition is to have baryon-number-violating interactions. This is a little bit tricky, because every particle physics reaction we’ve ever observed has neither created nor destroyed a baryon at all, nor even a fraction of a baryon. Every Standard Model reaction that has ever taken place, in fact, can only create or destroy a quark (of baryon number +⅓) if it creates or destroys an antiquark (of baryon number -⅓) as well. There is no reaction you can write down, based on what we know today, that will lead to either the creation or destruction of even one baryon, much less some ~1079 baryons, which is approximately the number of protons-and-neutrons that exist within our observable Universe today.

However, baryons exist, implying that their creation (also known as baryogenesis) did occur at some point in the Universe’s past, as we are extremely confident that there are no regions of the Universe that are antimatter-dominated just as ours is matter-dominated. Within the Standard Model, there may be a way out of this dilemma, however: neither the number of baryons (like protons and neutrons) nor leptons (like electrons) are required to be strictly conserved within the Standard Model, but only the difference between them. In other words, it should be possible to create a net number of baryons along with an equal net number of leptons under the proper conditions.
So to recap: if you want to create a net number of baryons (and leptons) from an initially symmetric state, you have to meet all three of the Sakharov conditions. The first, being out of thermal equilibrium, is a given in an expanding and cooling Universe. The second, requiring C-violation and CP-violation, is only known to occur in the weak interactions, and only in amounts far too small to account for the observed matter-antimatter asymmetry; there must be additional sources of CP-violation beyond what has been observed. And the third, of baryon number-violating interactions, can occur within the Standard Model, but only under specific circumstances, all of which still require that the combination of “baryon number minus lepton number” remains preserved.
After extensive research into the problem of baryogenesis, physicists have uncovered four possible mechanisms by which we could have generated a matter-antimatter asymmetry from initially symmetric conditions.
- You can have a grand unification scenario, where new super-heavy fundamental particles, including the X-and-Y bosons, exist, and if they decay through CP-violating channels, can create a baryon excess over antibaryons.
- You can have the leptogenesis scenario, where new physics in the lepton-and-neutrino sectors, at very high energies, produce an excess of leptons over antileptons, and then the sphaleron interactions (which preserve baryon number minus lepton number) convert a portion of that lepton excess into a baryon excess.
- You can have a scenario known as electroweak baryogenesis, where the process of electroweak symmetry breaking occurs via a severe phase transition, and a baryon asymmetry can arise from this. (Although, it should be noted that the LHC, which could be sensitive to this scenario, hasn’t seen any evidence for it.)
- Or you can have a scenario known as Affleck-Dine baryogenesis, which is based on the combined ideas of cosmic inflation (which has a copious amount of evidence for it) and supersymmetry (which has no evidence for it, and mountains of null results to show for all the searches for it).
All of these involve new physics, and it’s possible that none of them are relevant for our Universe (i.e., that baryogenesis proceeded via a completely different mechanism than what we understand today.) Nevertheless, it’s instructive to see how a matter-antimatter asymmetry could have arisen, so let’s work through the grand unification scenario for baryogenesis.

In the image above, representing conditions shortly after the start of the hot Big Bang, we can imagine that yes: there are all of the particles and antiparticles, in equal, balanced numbers to one another, existing and creating and annihilating in rapid succession. In addition to those, because we live in a Universe where grand unified theories describe reality (the jury is still out on that), there are two new fundamental particles that exist:
- the X-boson, with a charge of +4/3,
- and the Y-boson, with a charge of -1/3,
- as well as their antiparticles (denoted with a bar over them) with equal-and-opposite charges to them.
Now, these are unstable particles, so as the Universe expands and cools, these particles decay. (This is why out-of-equilibrium conditions are important!) The X particles, for example, could decay to either two up quarks or to an anti-down quark plus a positron, which have a baryon number minus a lepton number of +⅔. (And the anti-X particles decay to two anti-up quarks or to a down quark plus an electron.) The Y particles, meanwhile, can decay to either an anti-up and an anti-down quark or to an up quark and an electron, with a baryon minus lepton number of -⅔. (And the anti-Y particles decay to an up and down quark or to an anti-up quark and a positron.)
The laws of physics mandate that a particle and its antiparticle counterpart all have the same decay channels. But if you can violate C and CP symmetries, what’s called the branching ratios — or the percentage of decays that follow each channel — can differ between particles and antiparticles, as illustrated below.
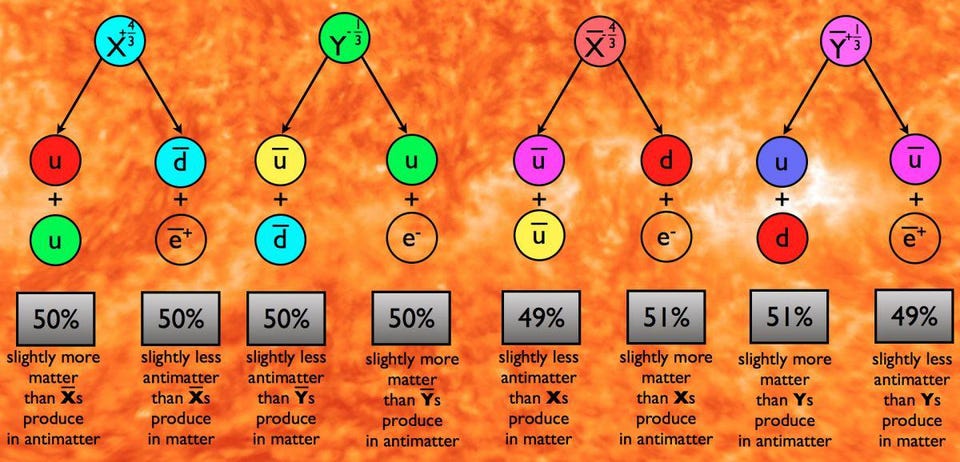
Let’s imagine we have 100 X particles, 100 anti-X particles, 100 Y particles, and 100 anti-Y particles that all undergo the decays above. After they all decay, we wind up with:
- 100 up quarks, 50 anti-down quarks and 50 positrons from the X-particles,
- 98 anti-up quarks, 51 down quarks and 51 electrons from the anti-X particles,
- 50 anti-up quarks, 50 anti-down quarks, 50 up quarks, and 50 electrons from the Y-particles,
- and 51 up quarks, 51 down quarks, 49 anti-up quarks and 49 positrons from the anti-Y particles.
Now, let’s allow those quarks, antiquarks, and electrons and positrons to annihilate away, and what are we left with?
For every 100 X/anti-X pairs and 100 Y/anti-Y pairs, we made a total of:
- 201 up quarks,
- 197 anti-up quarks,
- 102 down quarks,
- 100 anti-down quarks,
- 101 electrons,
- and 99 positrons,
leaving us, after annihilations, with a net of 4 up quarks, 2 down quarks, and 2 electrons: enough to make two protons (both baryons) and two electrons (both leptons). Just like that, from an initially symmetric state, we can create more matter than antimatter just through those three Sakharov conditions.
In all baryogenesis scenarios, it’s the out-of-equilibrium nature of the early Universe, along with the CP-violating nature of decays, that enable the creation of a baryon asymmetry from an initially symmetric Universe. This is the leading set of ideas for how we wound up with a matter-dominated Universe, but we still don’t know precisely how it occurred, as all of this is beyond the reach of even our best particle physics experiments. Perhaps, someday, this great open question in physics will finally be solved!
Send in your Ask Ethan questions to startswithabang at gmail dot com!