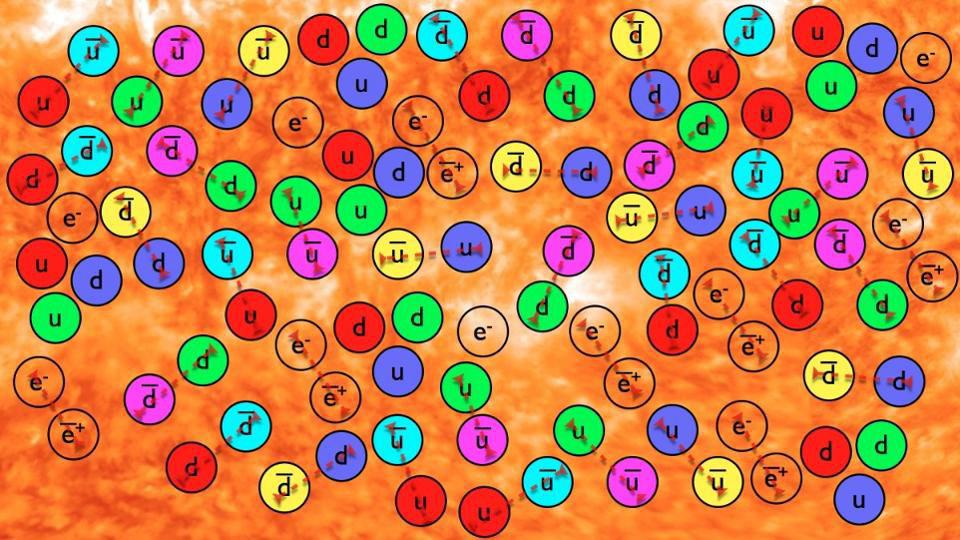
Ask Ethan: Why do matter and antimatter annihilate?

- Whenever interactions occur with enough free energy to admit the creation of new particles via E = mc², the creation process always makes equal amounts of matter and antimatter.
- Similarly, when matter encounters antimatter, they annihilate away into energy, which usually becomes photons but can sometimes become other particles (and antiparticles) as well.
- But why does this occur? Why annihilation, rather than the formation of bound states, simple scattering, or any other option? There’s a quantum reason we simply can’t avoid.
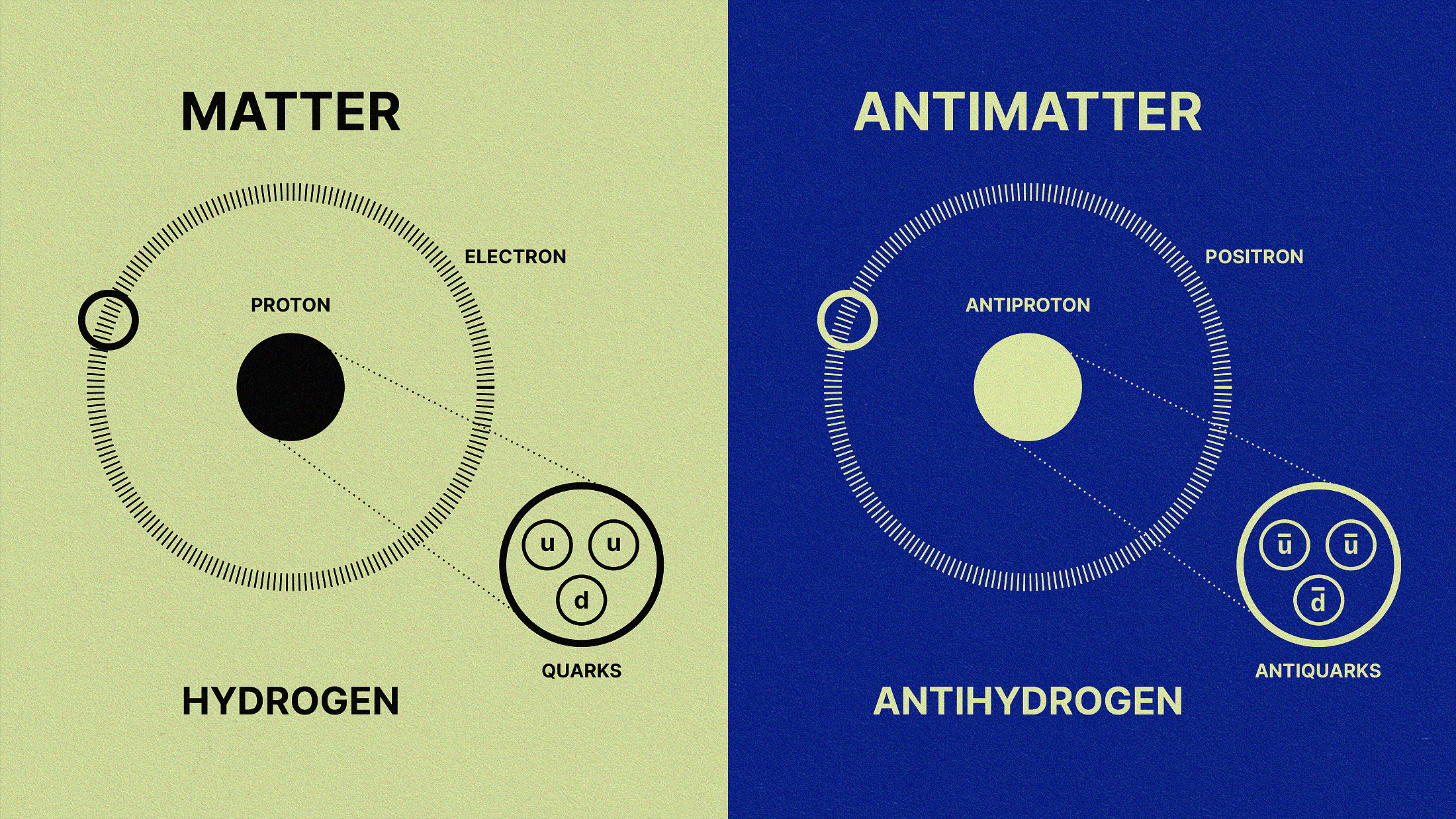
The matter that we’re made out of here on planet Earth is composed of atoms: protons and neutrons in the nucleus, orbited by electrons, that bind together in countless possible ways to produce what we experience as the world around us. For every fundamental and composite particle of matter that exists, however, there’s also its antimatter counterpart: antiprotons for protons, antineutrons for neutrons, positrons for electrons, etc. When matter and antimatter collide and interact, they annihilate, producing pure energy and whatever particles are allowed by the quantum laws that govern nature as well as Einstein’s most famous equation, E = mc².
But do matter and antimatter always annihilate away when they interact? Aren’t other types of interactions possible, and even likely? That’s what Brian Vant-Hull wants to know, writing in to ask:
“What physics principle mandates that matter and antimatter MUST annihilate when brought together? It makes sense that when matter is created, antimatter could (but does not need to) be created to satisfy the conservation laws. Time reversal suggests that an electron and positron CAN turn back into photons, but couldn’t they also form an electron-positron atom? Couldn’t a neutron and antineutron just bounce off each other?”
Matter-antimatter annihilation seems like an inevitability, but does it really happen 100% of the time? And when they do annihilate, what’s the physics principle mandating that they do so? They’re fascinating questions, and one that physics does indeed hold the answer to. Let’s investigate.

Whenever two particles come into the vicinity of one another, there’s an opportunity — but not a certainty — that they’ll interact. The way you determine the probability of an interaction is by measuring what’s known as a cross-section: the amount of effective area that one particle has to “hit” the other. We know that particles like protons and neutrons have a specific size: a little bit under a femtometer (10-15 meters) in radius, while electrons are confirmed to be point-like, with a minimum radius that must be smaller than a tenth of an attometer (10-19 meters): a figure that we know thanks to deep inelastic scattering experiments.
You might think that given the size of these objects, you can estimate their cross-sections simply by assuming they’re spheres with a specific radius, and that they’ll have a cross-sectional area given by the area of a circle: πr². That would be extremely reasonable if you’re thinking classically: by treating these particles like they’re billiard balls, for example.
But that assumes that the way particles and antiparticles interact is simplistic and classical: that they “bounce off” one another the way billiard balls do, and that like billiard balls, if they aren’t perfectly aligned with one another and don’t physically collide, they won’t interact. And that’s not true at all.
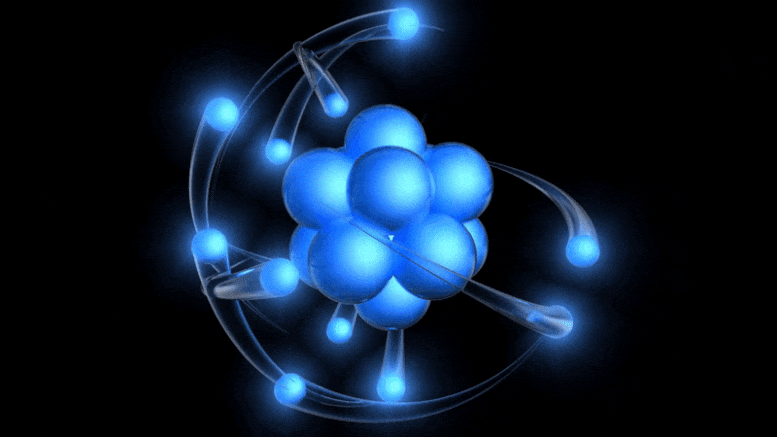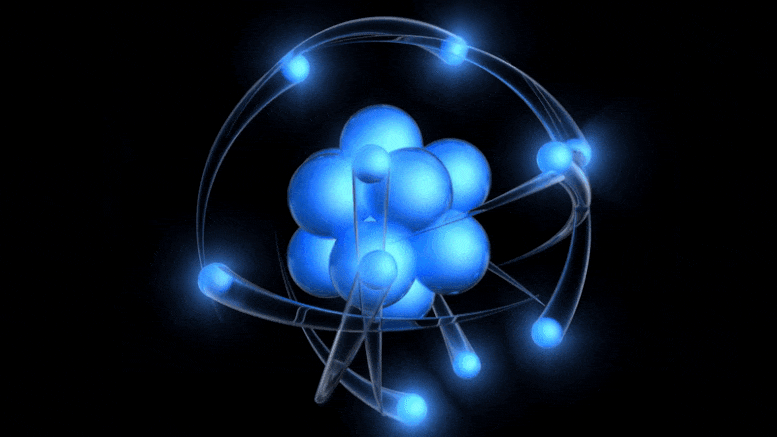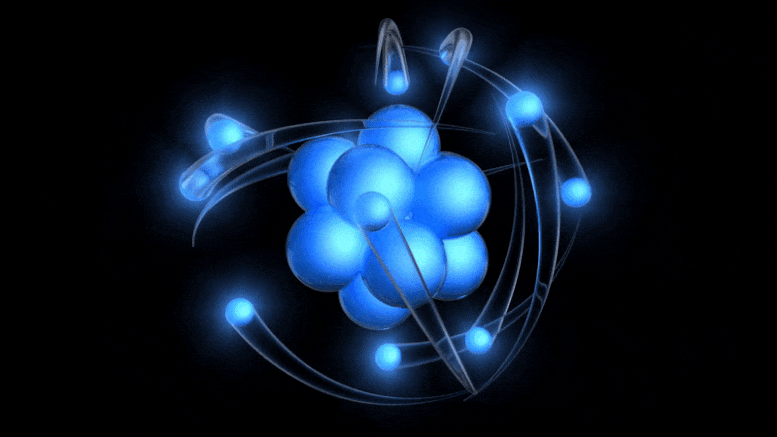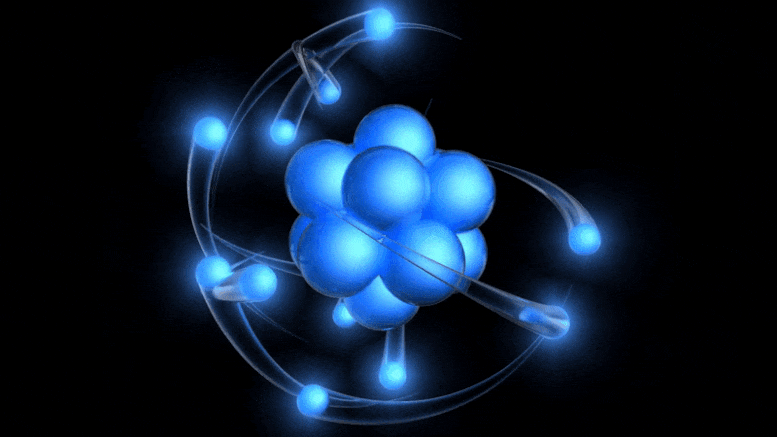
Consider, for example, the formation of a neutral atom from a free proton and a free electron. Protons are only about a femtometer in size, while electrons are even smaller entities. But you don’t need to make an electron collide with a proton in order to form an atom; you simply need the electron to have a close-enough encounter with the proton — coming within perhaps an ångström (10-10 meters) of it — in order for the quantum process of forming a bound, neutral atom. As the proton and electron interact electromagnetically:
- a quantum of radiation, a photon, is spontaneously emitted,
- as the electron forms a bound state with the proton (an excited atom),
- and then the electron cascades down the various energy levels inside the atom,
- emitting a photon at each stage,
- until it reaches the ground-state, becoming a stable, neutral hydrogen atom.
In other words, because there exists a bound state between these two particles, the proton and electron, we have to consider the possibility that instead of just “bouncing off of” each other, like particles would in a typical scattering event, they can form this bound state by interacting in a particular way: electromagnetically. Additionally, because these are quantum particles (and not “classical” particles that always behave in a billiard ball-like fashion), we can’t simply treat them as spheres with a particular cross-section.
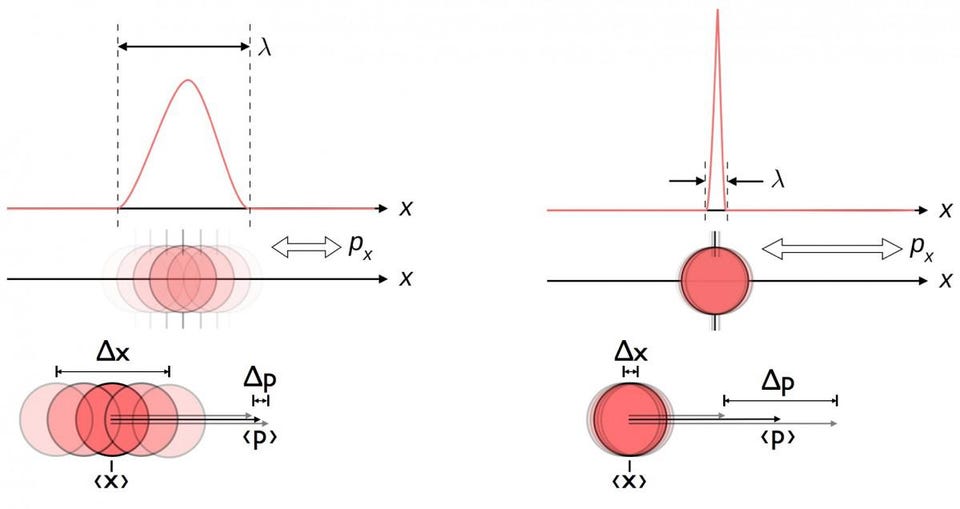
Instead, we have to recognize that these particles, regardless of how quickly or energetically they’re traveling with respect to one another, are inherently quantum particles in nature. (This will apply equally to antiparticles as well; it doesn’t matter whether we’re talking about matter or antimatter specifically.) Because they’re quantum in nature, that means their positions cannot be defined exactly, but rather has an inherent uncertainty to it: an uncertainty that increases the more well-known each particle’s (or antiparticle’s) momentum is known. Specifically, this is due to one incarnation of the the Heisenberg uncertainty principle, which tells us that:
- Δx Δp ≥ ℏ/2,
where x is position, p is momentum, and ℏ is Planck’s constant.
Whenever there’s an overlap between the wavefunction of two (or more) quanta, there are two ways of approaching the problem. We can approach it from a theoretical perspective, where we use quantum field theory to calculate things like cross-sections, amplitudes, and the probabilities of producing a variety of end-states, including things like simple forward (bouncing-off) scattering, transitioning into a bound state (whether stable or not), or interacting and/or annihilating into a wide variety of products. In physics, every outcome that’s not explicitly forbidden must have its probability, no matter how small, taken into account.

We can also approach things from the experimental perspective: where we simply measure these quantities directly: including forward scattering, forming a bound state, and for the case of matter-and-antimatter, the possibility of annihilation into a variety of decay products. Contrary to what you might think or expect, matter-antimatter annihilation isn’t something that necessarily happens 100% of the time.
Take a proton and its antimatter counterpart, for example: the antiproton. This was the bread-and-butter of the world’s most powerful particle accelerator and collider just prior to the launch of the Large Hadron Collider at CERN (which collides protons with protons instead): the TeVatron at Fermilab. When you launch a proton and an antiproton at one another at a variety of speeds/energies, you might be surprised at what you measure. The cross-section that you find, experimentally, is not well-represented by just a single value, which is what you’d expect if protons and antiprotons behaved like billiard balls.
Instead, what you find is that the cross-section is energy-dependent, and energy-dependent in a counterintuitive way. At high energies, like at ~200 GeV or above (energies greater than the rest-mass energy of any and all Standard Model particles), the proton-antiproton cross-section is identical to the proton-proton cross-section, like it doesn’t matter whether one is matter and the other is antimatter or not.
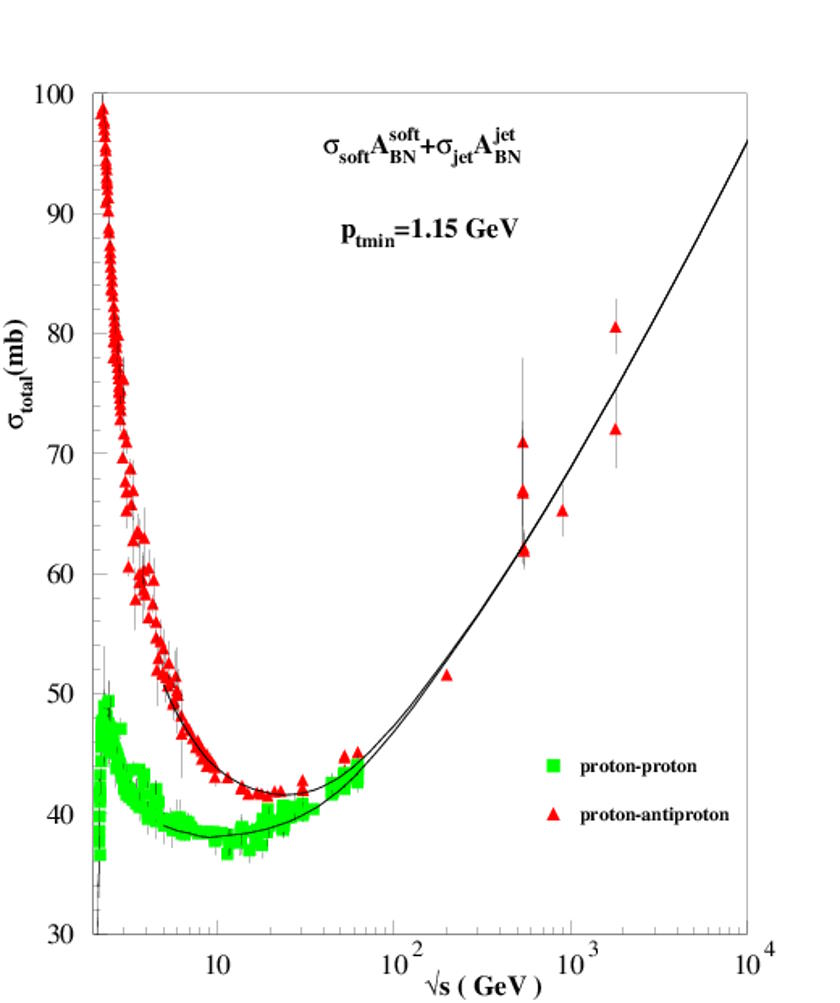
But at lower energies, the cross-section for proton-antiproton collisions or interactions is much greater than it is for protons and other protons, as at low momenta, there’s more time over which a proton and antiproton’s wavefunctions have to overlap and allow the possibility that at least one of the matter-based quarks inside the proton (up, up, and down) can interact with at least one of the antiquarks inside the antiproton (anti-up, anti-up, and anti-down). For historical reasons, particle physicists measure cross-sectional areas in quantities known as barns, as in you’re trying to “hit the broad side of a barn.”
In reality, a barn is a unit of (typically nuclear) cross-sections that correspond to a tiny square that’s 10 femtometers (or 10-14 meters) on a side. 10 millibarns, which is the interval between numbers on the y-axis on the graph above, corresponds to a tiny square that’s one femtometer (10-15 meters) on a side. At these low energies and low momenta, proton-antiproton interactions are far more common than proton-proton interactions, which makes sense. Protons have positive charges, and so two protons will electrically repel each other. An antiproton has a negative charge, so a proton-antiproton pair will attract one another. And, since an antiproton has the same charge as an electron, you might think that it’s possible to form a bound state between protons and antiprotons as well, just as a proton and an electron form an atom.
This actually occurs in nature! Known as either protonium or antiprotonic hydrogen, it’s a species of exotic atom where a proton and antiproton are bound together through the electromagnetic interaction. Both high-energy particle collisions that produce antiprotons (including from the production of proton-antiproton pairs) as well as manipulation of protons and antiprotons inside a magnetic cage are methods for producing protonium. At very low energies, at ~1 keV and under (about a millionth of the rest-mass energy of protons), it becomes possible to form protonium, which has a mean lifetime of about a microsecond and a binding energy of -750 eV.
Why does protonium have a lifetime of just ~1 microsecond?
For the same reason that the proton-antiproton annihilation cross-section increases so thoroughly at low energies: because these particles cannot be meaningfully treated as billiard balls! Again, this proton and this antiproton are behaving as wavefunctions, and at the tiny separation distances they’re located at (just 1/2000th the size of a standard hydrogen atom) with respect to one another, those wavefunctions overlap substantially. The mean lifetime of ~1 microsecond corresponds to how long, on average, protonium takes before the proton and antiproton within it overlap, and decay away through annihilation: either into two photons or into jets (of hadrons, most popularly pions) of quark-antiquark containing particles.
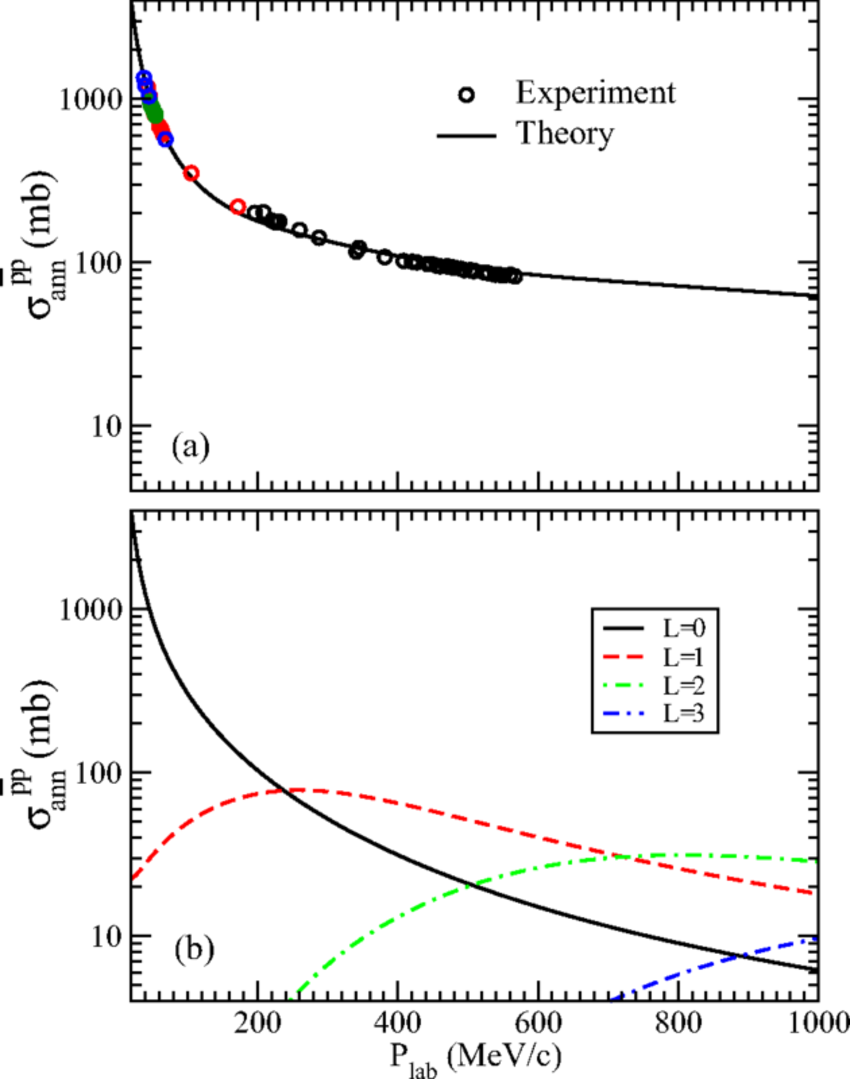
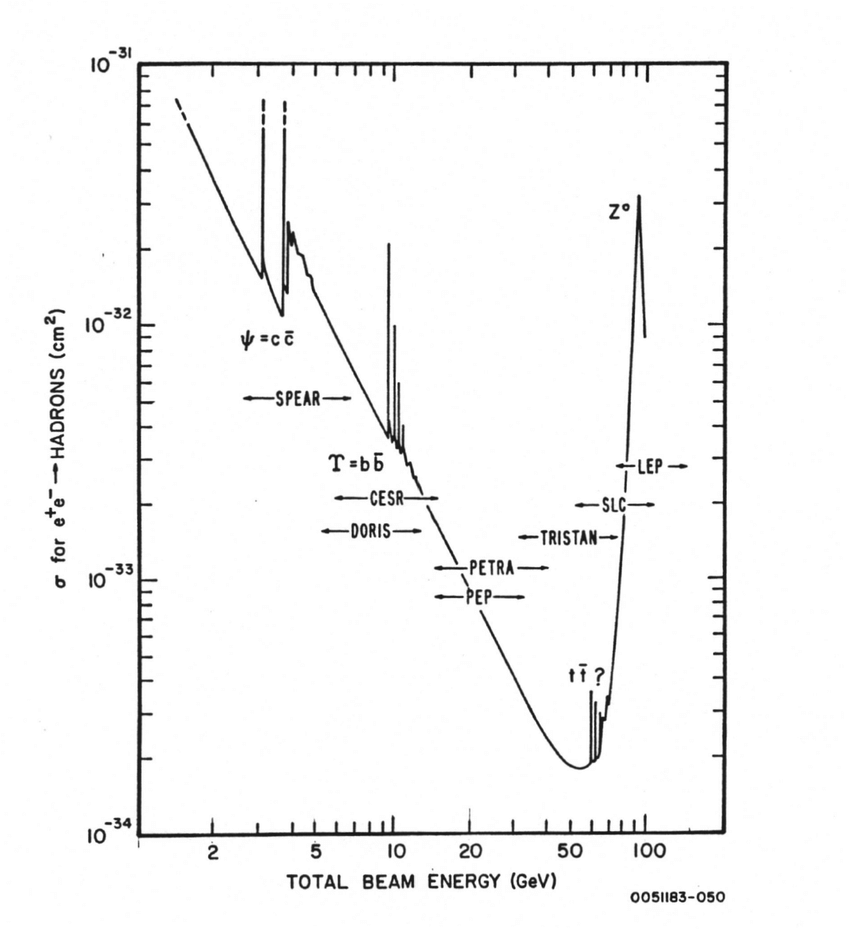
It’s remarkable that both experiment and theory agree when it comes to the annihilation cross-section for protons with antiprotons, as it confirms that our quantum field theories for even these composite particles align with what our Universe actually delivers to us. We can go to a different type of matter-antimatter as well: two point-like electrons. Whereas you might be able to hand-wave some justification for why protons and antiprotons, each about ~femtometer-sized individually, have an annihilation cross-section that’s measured in tens-to-thousands of millibarns, for electrons and positrons, each of which must be physically ~10,000+ times smaller than protons or antiprotons, this is clearly impossible.
It’s true: the electron-positron cross-section is suppressed significantly when compared to the proton-antiproton cross-section, but only by a factor of ~1,000,000 or so. Electrons and positrons are actually very similar to protons and antiprotons in a number of ways.
- At low-energies, they have higher interaction cross-sections than at intermediate energies.
- They can form bound states: electron-positron bound states are known as positronium, as opposed to protonium for protons and antiprotons, with a mean lifetime of around ~1 microsecond.
- At high energies, they still interact, but the cross-section is no different than for electron-electron interactions.
Only, when electrons and positrons annihilate, 100% of their energy goes into the production of new particles, as they’re point-like rather than composite particles made of quarks (or antiquarks) and gluons.
When people talk about building future colliders, one of the most popular ideas is to build a lepton collider. In fact, there are three main designs typically considered:
- an electron-positron linear collider,
- an electron-positron circular collider,
- and a muon-antimuon circular collider.
The linear collider option is the cheapest in terms of construction cost, but has the drawback that you only get one chance for each electron-positron bunch to collide: at the collision point where they meet. With a low inherent electron-positron cross-section, most of them miss. A circular collider, although more expensive to build, offers the opportunity to circulate your leptons in one direction and your antileptons in the opposite direction, allowing them to repeatedly pass one another in bunches until they do actually collide at a specific point that you’ve built your detector around.
The fact that electrons and positrons don’t always collide is why we have to deal with that concern. In accelerator physics, you need large statistics, and a large number of events, to build up evidence for new particles and their properties. Muons and antimuons offer higher energies, but because they’re unstable and decay with a mean lifetime of ~2.2 microseconds (and are more difficult to create, collimate, and accelerate), they can only offer much lower luminosities, or total numbers of collisions, than comparable electron-positron colliders.
It isn’t that there’s a physical principle that mandates, “Whenever you have matter and antimatter, they must annihilate,” because they don’t always do that. All particle species of matter (and all antiparticle species of antimatter) only have a finite cross-section with their antiparticle (or particle) counterparts: one that happens to be an energy-dependent cross-section. Sometimes, you simply get purely elastic scattering, as though these particles were billiard balls. Sometimes, at low enough energies, they can form bound states, such as protonium (for proton-antiproton pairs) or positronium (for electron-positron pairs), which can persist for a relatively long time in the world of particles: up to a microsecond or so.
But there’s an enormous cross-section (or chances of an interaction), both at extremely low energies and at extremely high energies, that will cause matter and antimatter particles to annihilate with one another, with the energy of the collision plus the rest-mass energy of each particle that annihilates, determining how much energy is available for new particle (or particle-antiparticle) creation: via Einstein’s E = mc². Even though we think of protons (and antiprotons) as having a particular size and electrons (and positrons) as being point-like, their actual cross-sections are energy-and-momentum dependent, and require that we treat these particles as quantum entities: with spread-out wavefunctions in space that overlap, and that have a chance of quantum-tunneling into another state.
The reason the annihilation rate (or cross-section) is so large is due to the quantum nature of particles, and to the Heisenberg uncertainty principle, with the uncertainty in position being of paramount importance. It’s further proof that our old, classical way of conceptualizing the Universe is outdated, and emphasizes just how important quantum processes are in practically every subatomic process we can imagine!
Send in your Ask Ethan questions to startswithabang at gmail dot com!