Ask Ethan: Will everything eventually succumb to Hawking radiation?

- It was long thought that black holes, once they formed, would be stable forever, but that story changed significantly with the work of Stephen Hawking in 1974.
- Black holes actually emit tiny amounts of radiation continuously, and on enormously long timescales of ~10^67 years or greater, they’ll eventually evaporate away entirely.
- In 2023, a provocative paper suggested that this radiation isn’t limited to black holes, implying that everything eventually decays away. Now, a year-and-a-half later, here’s what we’re thinking about.
When black holes were first derived within the context of general relativity, it was thought to be an absolute, irrevocable end-state of a completely collapsed object. Aside from possessing mass, electric charge, and angular momentum, no other properties would matter, and so long as nothing else interacted with the black hole, those properties would persist — and would persist unchanged — forever.
That all changed, however, when people began treating the Universe as quantum in nature: with quantum fields (like the electromagnetic field) permeating all of space. This would include even the space around a black hole, and quantum effects in highly curved spacetime would lead to the gradual emission of radiation that now bears the name of the person who predicted it: Hawking radiation. On long enough timescales, even the most massive black holes would eventually evaporate away.
Last year, a fascinating new study suggested that Hawking radiation might not be for black holes alone, but would rather be produced by all masses that curved space by a significant enough amount. Is this still thought to be correct? That’s what Klaus Castren wants to know, as he asks:
“Could we have an update on the concept of Hawking radiation not originating only from a black hole’s event horizon, and that other massive objects would also produce it? I find the idea disturbing that all massive objects would do this (causing their eventual evaporation?) without us understanding how the particles they consist of would decay. What would a bowling ball floating eternally in infinite space look like once half of its mass would have been radiated out via Hawking radiation?”
Oh, it’s disturbing alright, and the answer to all of your questions is, “We still aren’t sure.” Let’s explore this topic as we consider why.

Hawking radiation is a fascinating phenomenon. It arises from the combination of two phenomena from very, very different areas of physics. First, in general relativity, we have the fact that space, at a fundamental level, has some very counterintuitive properties.
- It isn’t static, but rather dynamic, as its properties change as energy-containing objects (including masses) both exist within it and move through it.
- It isn’t universal, as a hypothetical observer sees the properties of space change dependent on their location.
- And it isn’t absolute, as your motion through space alters the property of space that you perceive.
If you moved far enough away from even a stupendously massive black hole, space would appear indistinguishable from flat, empty space; it would behave the way our familiar empty space does in a region where the curvature due to matter-and-energy was negligible.
But if you’re very close to the event horizon of a black hole, space doesn’t appear indistinguishable from flat. Instead, the curvature of space will alter your path, even if you’re in uniform motion, to follow the curvature of space that the black hole induces. You can still find yourself in free-fall, of course, but the path you take will no longer be a straight line. Instead, you’ll notice that your motion follows a curved trajectory, owing to the gravitation of the black hole.

Credit: ESO/MPE
Now, we come to the second part: the fact that space is filled with quantum fields. For any observer in their own inertial reference frame (i.e., in free-fall, with no external thrust or push acting on it), they’ll experience the quantum vacuum the same way we do: where you can extract things like particles or radiation from a sufficiently strong applied external field, or where you can observe subtle effects that belie its existence like the Casimir effect or the Lamb shift. Whether you were in free-fall very close to a black hole or very far away from it, you’d observe the same effects with the same magnitudes. So long as you’re in an inertial reference frame, there’s no difference that being close to or far from a black hole makes.
But this is where it gets both tricky and interesting. An observer close to a black hole might see their quantum vacuum behaving identically to how an observer far from a black hole sees their own quantum vacuum, but if you ask either observer about the quantum vacuum at the other observer’s location, they’ll tell you that they see a different vacuum at that other location. This is one of the remarkable aspects of combining general relativity (with its curved background of space) with quantum field theory (which describes quantum fields): these two effects together show us that the quantum vacuum differs between any two regions where the curvature of space is different from one region to the other.

In 1974, Hawking became the first person to put those facts together: that the quantum fields in a region of spacetime that’s highly curved (near a black hole) and that’s indistinguishable from flat (far from a black hole) lead to a special type of radiation. Acceleration is acceleration, and it was also discovered at around the same time that any uniform acceleration through space will produce a “bath of radiation” for the observer, with the temperature and energy of the radiation dependent on the magnitude of the acceleration.
But this ties into the key realization that led Einstein to general relativity in the first place: the equivalence principle!
Einstein had already discovered the special theory of relativity, determining that the speed of light was the thing that was constant for all observers, rather than their perceptions of time and space. However, he recognized that his theory didn’t incorporate gravitation, but only motion. But since gravity is a real phenomenon in our Universe, Einstein began thinking about gravity as a form of acceleration. He asked himself, as a hypothetical, what the difference would be between two observers that were each in a locked, windowless room, where one was stationary on the surface of the Earth and the other was accelerating upward, due to some sort of thrust, at the same magnitude that Earth’s gravity accelerates objects at its surface.

Einstein swiftly realized that, to the observer inside, there was no difference. He later referred to this as his happiest thought, noting that it had him so excited that he didn’t sleep a wink for the next three nights. This principle, known as Einstein’s equivalence principle, paved the way for general relativity. Later, it would hold special relevance for the phenomenon of Hawking radiation, as if an accelerated observer in empty space experienced a bath of uniform radiation, then an observer who accelerated due to their close proximity to a black hole should also experience a bath of uniform radiation. Moreover, the closer you got to a black hole’s event horizon, the greater your acceleration, and hence, the more energetic the radiation that you’d experience would be.
Think about what this means.
- Far away from the black hole’s event horizon, there’s practically no acceleration, and so practically no energetic radiation would exist.
- As you start to approach the black hole’s event horizon, your acceleration increases, and so you begin to see more abundant radiation that’s greater in energy.
- And as you are about to reach the event horizon, your acceleration increases still further, and so the radiation reaches its peak in both flux and energy.
Just as the curvature of space increases, so does your acceleration toward the central region of a black hole. And, alongside it, the amount of radiation in that region of space increases as well.

There are several important things to notice about this picture we’re creating in our heads. First off, there is no mention of the “particle-antiparticle pairs” analogy so often used by Hawking, as that flawed analogy is irrelevant to the production of the radiation. Second, the Hawking radiation that is produced isn’t confined to being right at the event horizon, but rather should emerge from any region of space that has sufficient spatial curvature, or that induces strong enough accelerations. And third, just as Einstein noted one couldn’t tell the difference between being in a windowless room that accelerated due to thrust versus one that accelerated due to gravity, there should also be no difference between the space outside of a black hole and the space at the same distance away from any other equivalently-massed object.
That last part is a bit counterintuitive to many, but it’s true!
If you’re located a certain distance away from a mass (which can also have charge and/or angular momentum), then that mass could be:
- a point (like a black hole),
- a very compact but non-collapsed object (like a neutron star),
- a less compact object (like a white dwarf),
- or a non-compact object (like a star),
and you would experience the same acceleration at that location, with the same spatial curvature. So long as the masses of those different objects are identical and your distance from the center-of-that-mass is identical (and you’re not physically inside any part of the object itself), you shouldn’t experience any detectable difference between these scenarios.

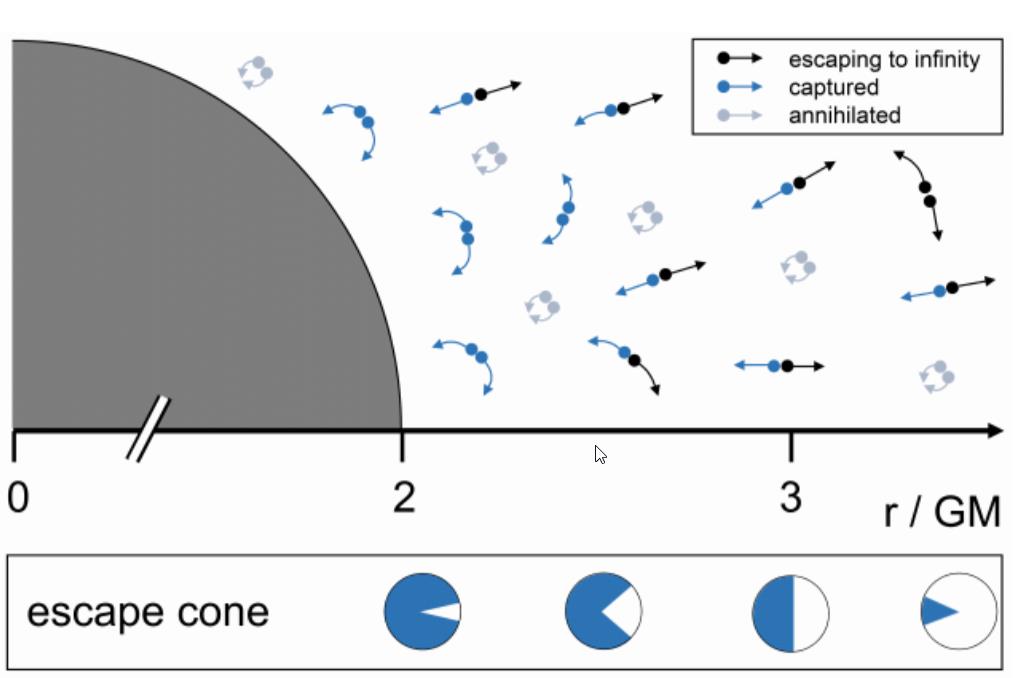
That’s what made this 2023 study so interesting: the authors contended that if black holes produced Hawking radiation, then so should neutron stars, white dwarfs, normal stars, and any other object. They argued that the only role the event horizon itself — found only in black holes and never in any other object — plays is to serve as a boundary for where radiation can be captured versus where that radiation escapes from. The event horizon serves as the boundary for a black hole; the neutron star’s surface serves as the boundary for a neutron star; the outermost layer of a white dwarf serves as the boundary for a white dwarf; the end of a star’s photosphere serves as the boundary for a star.
In all cases, the authors argued, there would still be energetic radiation that was produced from the curved spacetime around the mass. The fraction of that radiation that escaped from a massive object, emitted into the greater Universe as Hawking radiation, would depend solely on the mass and radius of the object itself, with nothing notable being special about the event horizon’s boundary in particular.
Just as the Schwinger effect allows you to produce real particles that carry real energy from a region of space that possesses a sufficiently strong electric field, the gravitational effect of Hawking radiation around a black hole should enable the production of real radiation, with the amount of radiation that escapes depending only on the strength of the gravitational field over the relevant regions of space.
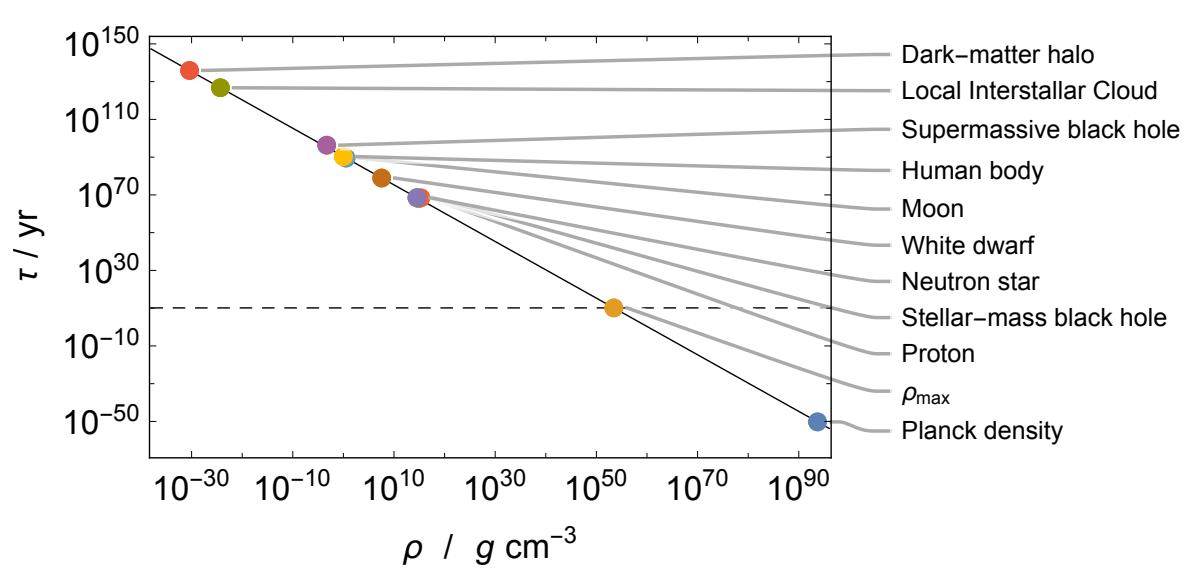
It’s a remarkable set of thoughts that leads to fascinating consequences, if true. As the same team of authors showed in a follow-up paper in October of 2024, if the spacetime curvature alone (and not the presence of an event horizon) is all that’s required to produce real, energy-carrying Hawking radiation, then compact stellar remnants such as neutrons stars and white dwarfs will eventually decay. The timescale for an object to decay (t) is related to the mass density (ρ) by the relation t ~ ρ-(3/2), meaning that white dwarfs require a much longer timescale for decay than black holes do, but a neutron star, whose outer surface is only modestly larger than an equal-massed black hole’s event horizon, have a maximum age of ~1068 years: comparable to the lifetimes of the lowest-mass black holes.
This would lead, potentially, to enormous consequences for all objects in the Universe: from the cosmic to the quantum. On similar timescales, the lowest-mass black holes, typical neutron stars, and even the proton itself should decay: around ~1067 years. White dwarfs should live longer: more like ~1080 years, while Earth’s Moon (smaller than most white dwarfs but far less dense) would take more like ~1090 years. The heaviest supermassive black holes require around ~10103 years, but something puffy and diffuse, like an interstellar gas cloud or, even worse, a dark matter halo, would require even longer timescales: between 10120 and 10140 years.
However, there are deep fundamental questions about the need for a horizon to radiate. For one, if the object radiates but lacks a horizon, where does the energy for the radiation come from? In general relativity, you are required to be able to trace the world-lines of each particle not just forward in time from some moment, but backward, too. For a black hole, that leads all outgoing radiation — even radiation that’s far from the event horizon — back to the event horizon at some point. For a horizonless object, that means the energy must come from some other source: the gravitational field or from composite particles (like protons) within the object. Once the gravitational field’s extractable energy is exhausted, then this relies on things like “proton decay” actually being possible within our Universe, which has never been demonstrated.
When an object has a solid surface, the geometry (spatial curvature) meets the source (the edge of the object), and the energy has a finite lower bound. It’s the presence of the event horizon, and specifically the fact that the black hole has an interior, that removes that finite lower bound. This raises the question of whether this decay will actually proceed without such a horizon. Others have noted that without a horizon — or, at least, an apparent horizon — the effects should be exponentially expressed. Only because the authors consider the radiation to emerge from a massless scalar (easy to calculate, but not among the known particles in the Standard Model) is that exponential suppression avoided.
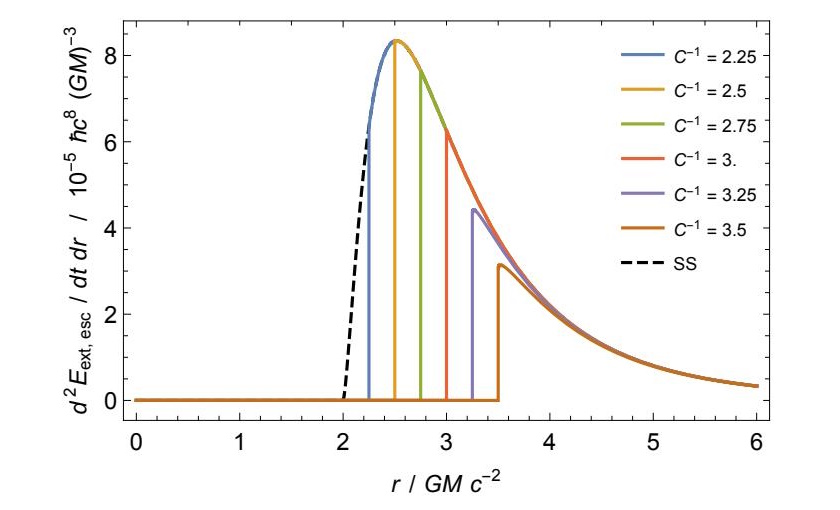
These arguments aren’t necessarily dealbreakers, though; perhaps the authors are correct, after all. Considering a massless scalar may not be problematic, since the physically real particles that overwhelmingly compose Hawking radiation are photons and gravitons: massless (non-scalar) particles in their own right, that may well behave just as a massless scalar does. The way black holes are thought to get lighter relies on physics that happens beneath the event horizon; can normal masses without horizons do something that’s equivalent? It’s not an answered question; it’s one that requires more work, as the answers are unknown to all at this point.
However, the arguments on both sides of the issue remain compelling, and it will take a significant amount of future work to determine whether non-black hole evaporation truly occurs. Perhaps the most difficult task associated with the endeavor will involve working out whether proton decay can actually occur; with only ~1058 protons in our entire Solar System, it would take billions of years of continuously monitoring every single one just to have a chance at catching one suspected decay event. Hawking radiation is a certainty for black holes, but we must now strongly consider the possibility that its effects apply to potentially even all massive objects. How profound is this consideration? The ultimate stability of practically everything in the Universe hangs in the balance.
Send in your Ask Ethan questions to startswithabang at gmail dot com!