3 independent proofs that quantum fields carry energy

One of the biggest questions that appears right at the intersection of physics and philosophy is as simple as it is puzzling: what is real? Is reality simply described by the particles that exist, atop a background of spacetime described by General Relativity? Is it fundamentally wrong to describe these entities as particles, and must we consider them as some sort of hybrid wave/particle/probability function: a more complete description of each “quantum” in our reality? Or are there fields, fundamentally, that underpin all of existence, where the “quanta” that we typically interact with are simply examples of excitations of those fields?

When quantum mechanics arrived on the scene, it brought with it the realization that quantities that were previously thought to be well-defined, like:

• the position and momentum of a particle,
• its energy and location in time,
• and its angular momentum in each of the three spatial dimensions that we have,

could no longer be assigned values, only a probability distribution for what values they could take on. Although this weirdness, on its own, brought about many arguments over the nature of reality, things would soon get even weirder with the introduction of quantum fields. For generations, physicists argued whether those quantum fields were actually real, or whether they were simply calculational tools.

Nearly a full century later, we’re certain that they’re real for one unambiguous reason: they carry energy. Here’s how we found out.

This diagram illustrates the inherent uncertainty relation between position and momentum. When one is known more accurately, the other is inherently less able to be known accurately. Both position and momentum are better described by a probabilistic wavefunction than by a single value. Other pairs of conjugate variables, including energy and time, spin in two perpendicular directions, or angular position and angular momentum, also exhibit this same uncertainty relation.

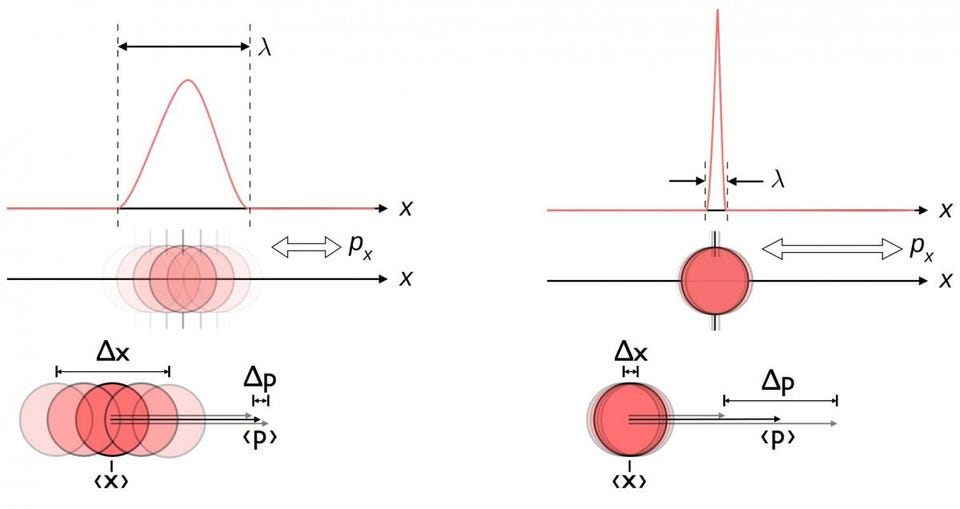
Quantum field theory came about because of an inconsistency in quantum mechanics as it was originally understood. Instead of having physical properties like “position” and “momentum” simply be quantities that were inherent properties of a particle that possessed them, quantum mechanics allowed us to understand that measuring one inherently induced an uncertainty in the other. We could no longer treat them as “properties” but rather as quantum mechanical operators, where we could only know what the probability of the set of possible outcomes could be.

For something like position and momentum, those probability distributions would have a time-dependence: the positions you’d be likely to measure or the momenta that you’d infer a particle possessed would change and evolve with time.

But this ran into another problem that we couldn’t avoid once we understood Einstein’s theory of relativity: the notion of time is different for observers in different reference frames. The laws of physics must be relativistically invariant, giving the same answers regardless of where you are and how fast (and in what direction) you’re moving.

Different frames of reference, including different positions and motions, would see different laws of physics (and would disagree on reality) if a theory is not relativistically invariant. The fact that we have a symmetry under ‘boosts,’ or velocity transformations, tells us we have a conserved quantity: linear momentum. The fact that a theory is invariant under any sort of coordinate or velocity transformation is known as Lorentz invariance, and any Lorentz invariant symmetry conserves CPT symmetry. This notion of invariance under constant motion dates all the way back to the time of Galileo.

The problem is that old-school quantum mechanics, like that described by the Schrödinger equation, yields different predictions for observers in different reference frames: it’s not relativistically invariant! It took years of development before the first equations that described the quantum behavior of matter in a relativistically invariant manner were written down, including:

• the Klein-Gordon equation, which applied to spin-0 particles,
• the Dirac equation, which applies to spin-½ particles (like electrons),
• and the Proca equation, which applies to spin-1 particles (like photons).

Classically, you’d describe the fields (like electric and magnetic fields) that each particle generates, and then each quantum would interact with those fields. But what do you do when each field-generating particle has inherently uncertain properties to it, like position and momentum? You can’t simply treat the electric field generated by this wave-like, spread-out electron as coming from a single point, and obeying the classical laws of Maxwell’s equations.

This was what compelled us to advance from simple quantum mechanics to quantum field theory, which didn’t just promote certain physical properties to being quantum operators, but promoted the fields themselves to being quantum operators.

Neutrinos and antineutrinos are copious within this Universe, but we can only detect which flavor (electron, muon, or tau) the neutrino is when it interacts with another particle. During the in-between times, when it’s traveling, it’s in an indeterminate state.

With quantum field theory, an enormous number of already-observed phenomena finally made sense, as having field operators (in addition to “particle operators” like position and momentum) allowed us to explain:

• particle-antiparticle creation and annihilation,
• radioactive decays,
• quantum corrections to the electron’s (and muon’s) magnetic moments,

and much more.

But were these quantum fields just a mathematical description of the particles that truly made up our reality, or were they actually real, themselves?

One way to answer this question — about whether something is “real” or not — is to ask what you can do with it. Sure, we can’t measure the underlying fields themselves, but if we can do things like extract energy from them, use them to perform “work” (i.e., to move masses a certain distance through the application of a force), or coax them into a configuration where they result in a definitive, observable signature that’s unique to quantum field theory, that can prove their “realness.” As of early 2023, we already have three independent empirical, experimental proofs that quantum fields are, in fact, very real.

If you have two conductors with equal and opposite charges on them, it’s an exercise in classical physics alone to calculate the electric field and its strength at every point in space. In regular (Schrodinger-like) quantum mechanics, we discuss how particles respond to that electric field, but the field itself is not quantized as well. This seems to be the biggest flaw in the original formulation of quantum mechanics.

1.) The Casimir Effect. In theory, there are quantum fields of all types — from the electromagnetic, weak, and strong nuclear forces — permeating all of space. One way to visualize this field is to imagine a series of quantum fluctuations, or waves, of all different possible wavelengths. Normally, in empty space, these wavelengths can take on any value, and do: what we call the “zero-point energy” of space, or the “ground state” of empty space, arises from the sum of all possible contributions.

However, you can imagine setting up barriers that restrict what sorts of waves and wavelengths are possible in a given region of space. In physics, we generally call these constraints “boundary conditions,” and they enable us to control all sorts of electromagnetic phenomena, including radio and television signals.

In 1948, physicist Hendrik Casimir realized that if one were to set up a configuration where two parallel conducting plates were held very close to one another, the “allowable” wave modes from outside the plates would be infinite, while inside the plates, only a subset of modes would be allowed.

The Casimir effect, illustrated here for two parallel conducting plates, excludes certain electromagnetic modes from the interior of the conducting plates while permitting them outside of the plates. As a result, the plates attract, as predicted by Casimir in the 1940s and verified experimentally by Lamoreaux in the 1990s.

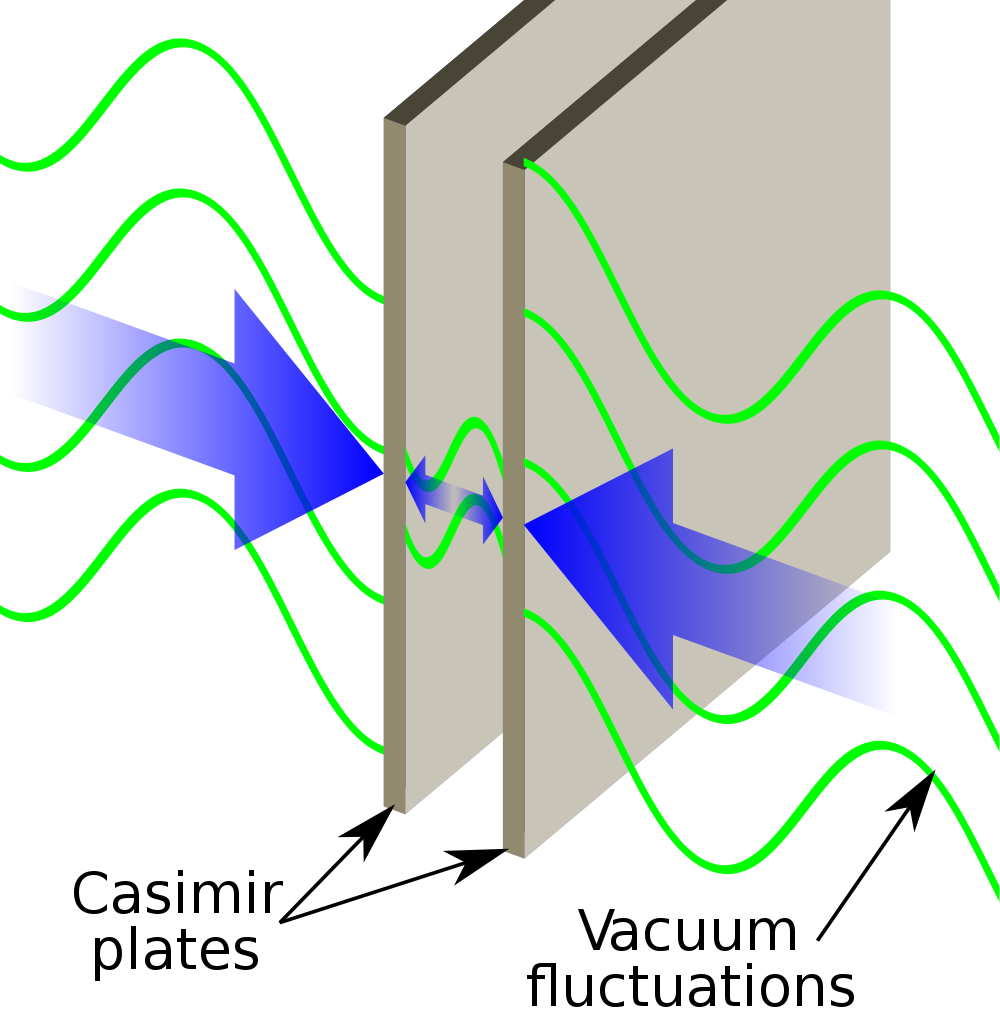
As a result, purely as an effect of the quantum fields between them, there would be a difference in the inward and outward forces acting on the plates, with the specific force dependent on the exact configuration. While it was generally accepted that the Casimir effect should exist, it turned out to be incredibly difficult to measure.

Thankfully, 49 years after Casimir proposed it, experiments finally caught up. In 1997, Steve Lamoreaux devised an experiment that leveraged a single flat plate and a section of an extremely large sphere to both calculate and measure the Casimir effect between them. Lo and behold, the experimental results agreed with the theoretical predictions to greater than 95% precision, with only a small error and uncertainty involved.

Since the dawn of the 2000s, the Casimir effect has been measured directly between parallel plates, and an integrated silicon chip has even been demonstrated to measure the Casimir force between even complex geometries. If quantum fields weren’t “real,” this very real effect would exist without explanation.

As electromagnetic waves propagate away from a source that’s surrounded by a strong magnetic field, the polarization direction will be affected due to the magnetic field’s effect on the vacuum of empty space: vacuum birefringence. By measuring the wavelength-dependent effects of polarization around neutron stars with the right properties, we can confirm the predictions of virtual particles in the quantum vacuum.

2.) Vacuum birefringence. In regions with very strong magnetic fields, empty space itself — despite not being “made” of anything physical — should become magnetized, as the quantum fields in that region of space will feel the effect of the external field. In the real Universe, pulsars actually provide this natural laboratory: generating magnetic fields that are several billions of times greater than even the strongest electromagnets we’ve created in labs on Earth. When light passes through this highly magnetized space, that light should become polarized as a result, even if the light was completely unpolarized to begin with.

The prediction of this effect, known as vacuum birefringence, goes all the way back to Werner Heisenberg. However, it wasn’t observed until 2016, when a team looked at a remarkably “quiet” neutron star located 400 light-years away: RX J1856.5-3754. This marked the faintest object for which polarization had ever been measured, and yet the degree of linear polarization was large and significant: 16%. Without the boosting effect of vacuum birefringence in the empty space surrounding this pulsar, this polarization cannot be explained. Yet again, the effects of quantum fields show up in an unambiguous, measurable place.

In theory, the Schwinger effect states that in the presence of strong enough electric fields, (charged) particles and their antiparticle counterparts will be ripped from the quantum vacuum, empty space itself, to become real. Theorized by Julian Schwinger in 1951, the predictions were validated some 70 years later in a tabletop experiment, using a quantum analogue system. Whether space can exist without these fields, or the energy that they possess in their ground state, is not yet answered.

3.) The Schwinger Effect. Instead of magnetic fields, imagine you’ve got an extremely strong electric field; something far stronger than you could ever make on Earth. Instead of magnetic polarization, the quantum vacuum would become electrically polarized: the same way charges migrate to opposite ends of a battery or other voltage source.

Within the depths of empty space, quantum fluctuations of all types occur, including the rare-but-important creation of pairs of particles-and-antiparticles. The lightest charged particles are the electron and its antimatter counterpart, the positron, and these are also the particles that accelerate by the greatest amounts (due to their low masses) in the presence of an electric field.

Normally, these particle-antiparticle pairs annihilate away back into “nothingness” before they can be detected. But if you turn up the strength of your electric field by a great enough amount, perhaps the electron and positron won’t be able to find one another again, because they’ll have been driven away from one another by the effects of the electrically polarized empty space that they exist in.

Graphene has many fascinating properties, but one of them is a unique electronic band structure. There are conduction bands and valence bands, and they can overlap with zero band gap, enabling both holes and electrons to emerge and flow.

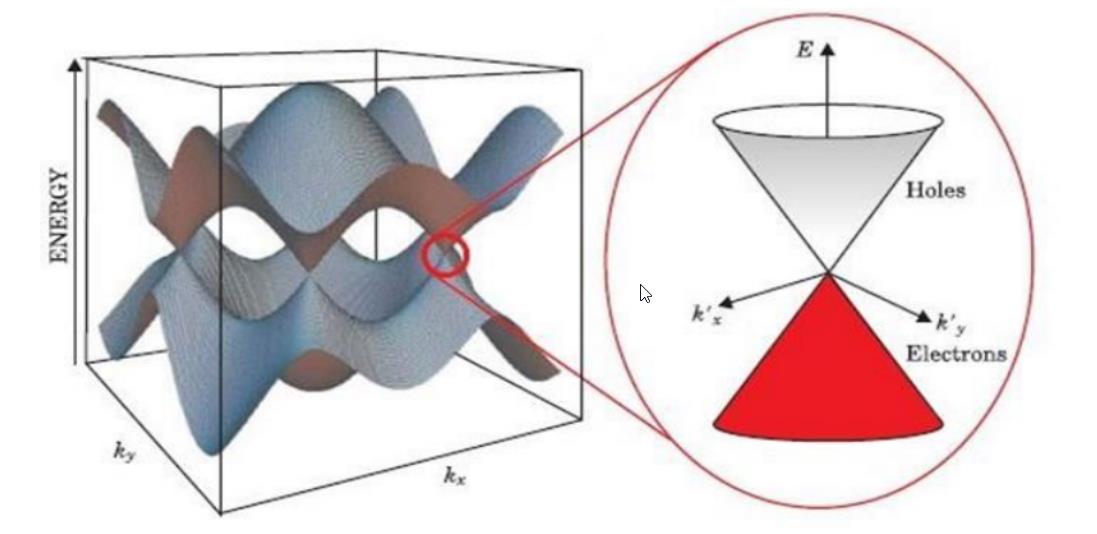
In theory, the very strong environments inside a neutron star should achieve these fields, and you could create new particle-antiparticle pairs out of the electric field energy via Einstein’s most famous equation: E = mc². We can’t perform experiments in that environment, however, nor could we recreate such conditions on Earth, and as a result, most researchers gave up on the idea of ever testing the Schwinger effect.

But in early 2022, a team of researchers did it anyway. By leveraging a graphene-based structure known as a superlattice — where multiple layers of materials create periodic structures — the authors of this study applied an electric field and induced the spontaneous creation of electrons and “holes,” which are the condensed matter analogue of positrons, at the cost of stealing energy from the underlying applied electric field.

The only way to explain the observed currents were with this additional process of spontaneous production of electrons and “holes,” and the details of the process agreed with Schwinger’s predictions from all the way back in 1951.

A visualization of QCD illustrates how particle-antiparticle pairs pop out of the quantum vacuum for very small amounts of time as a consequence of Heisenberg uncertainty. The quantum vacuum is interesting because it demands that empty space itself isn’t so empty, but is filled with all the particles, antiparticles, and fields in various states that are demanded by the quantum field theory that describes our Universe, even though this tool is a visualization only. If the vacuum becomes polarized, such as by having a charged particle nearby, then positive and negative charges will respond differently, effectively “screening” the space nearest to the charge from the charge itself.

Of course, one could argue that quantum fields needed to be real from the very start: since the first observation of the Lamb shift back in 1947. Electrons in the 2s orbital of hydrogen occupy a very slightly different energy level than electrons in the 2p orbital, which did not arise even in relativistic quantum mechanics; the Lamb-Retherford experiment revealed it even before the first modern quantum field theory — quantum electrodynamics — was developed by Schwinger, Feynman, Tomonaga and others.

Still, there’s something quite special about predicting an effect before it’s observed, rather than explaining an already-observed effect after the fact, which is why the other three phenomena stand apart from the initial impetus for formulating a quantum field theory.

One possible connection to the larger Universe is the fact that the observed effect of dark energy, which causes the accelerated expansion of the Universe, behaves identically to what we would expect if there were a small but positive, non-zero value to the zero-point energy of empty space. As of 2023, this is still speculation, as calculating the zero-point energy of space is beyond the present capability of physicists. Nevertheless, quantum fields must be considered real, as they carry energy and have both calculable and measurable effects on the light and matter within the Universe. Perhaps, if nature is kind, we might be on the cusp of discovering an even deeper connection.