The big theoretical problem of dark energy
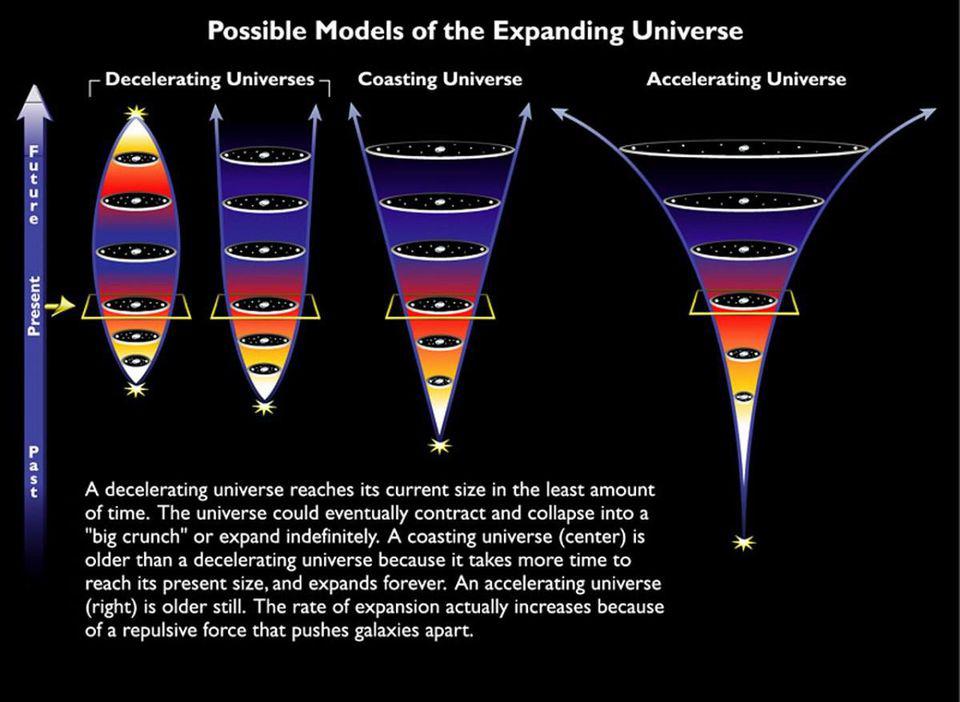
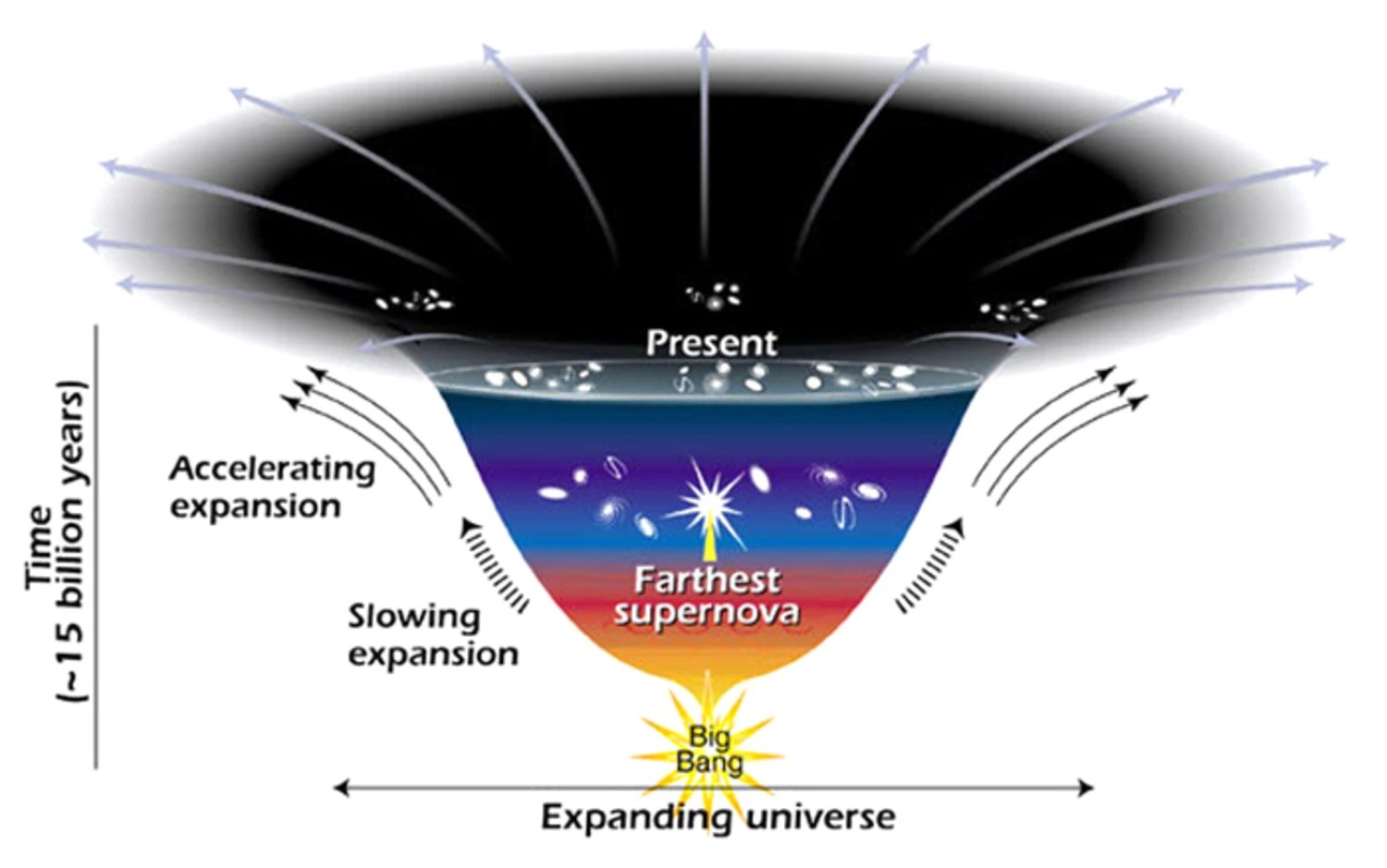
- Here in our expanding Universe, ultra-distant objects aren’t just speeding away from us, the rate at which they’re speeding away is increasing: teaching us that the Universe is accelerating.
- When we examine how the Universe is accelerating, we find that it’s behaving as though the Universe is filled with some sort of energy inherent to space: dark energy, or a cosmological constant.
- But theoretically, we have no idea how to calculate what the value of dark energy ought to be. Its extremely small but non-zero value remains a tremendous puzzle in fundamental physics.
One of the most fundamental questions we can ask about our Universe itself is “What makes it up?” For a long time, the answer seemed obvious: matter and radiation. We observe them in great abundances, everywhere and at all times throughout our cosmic history. For some ~100 years, we’ve recognized that — consistent with General Relativity — our Universe is expanding, and the way that the Universe expands is determined by all the forms of matter and radiation within it. Ever since we realized this, we’ve strived to measure how fast the Universe is expanding and how that expansion has changed over our cosmic history, as knowing both would determine the contents of our Universe.
In the 1990s, observations finally became good enough to reveal the answer: yes, the Universe contains matter and radiation, as about 30% of the Universe is made of matter (normal and dark, combined) and about ~0.01% is radiation, today. But surprisingly, about 70% of the Universe is neither of these, but rather a form of energy that behaves as though it’s inherent to space: dark energy. The way this dark energy behaves is identical to how we’d expect either a cosmological constant (in General Relativity) or the zero-point energy of space (in Quantum Field Theory) to behave. But theoretically, this is an absolute nightmare. Here’s what everyone should know.

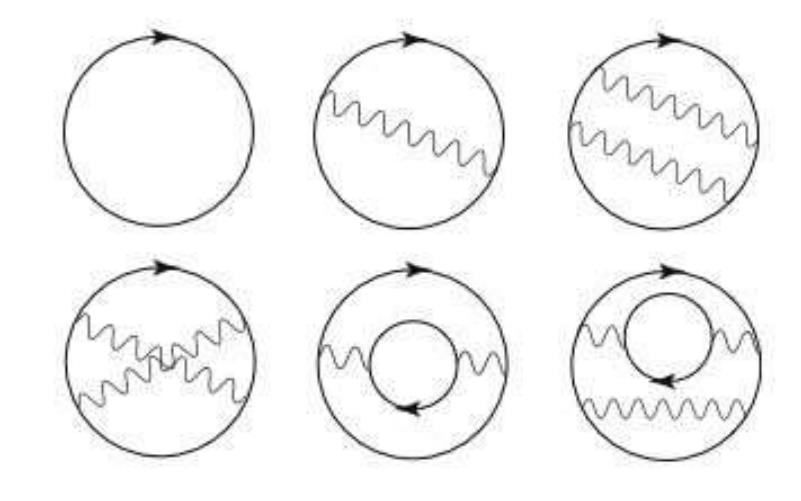
From a quantum point-of-view, the way we picture our Universe is that real particles (quanta) exist atop the fabric of spacetime, and that they interact with one another through the exchange of (virtual) particles. We draw out diagrams that represent all the possible interactions that can occur between particles — Feynman diagrams — and then calculate how each such diagram contributes to the overall interaction between the multiple quanta in question. When we sum up the diagrams in increasing order of complexity — tree diagrams, one-loop diagrams, two-loop diagrams, etc. — we arrive at closer and closer approximations to our actual physical reality.
But there are other diagrams as well that we can draw out: diagrams that don’t correspond to incoming-and-outgoing particles, but diagrams that represent the “field fluctuations” that occur in empty space itself. Just like in the case of real particles, we can write down and calculate diagrams of ever-increasing complexity, and then sum up what we get to approximate the real value of the zero-point energy: or the energy inherent to empty space itself.
Of course, there are a truly infinite number of terms, but whether we calculate the first one, the first few, or the first several terms, we find that they all give extremely large contributions: contributions that are too large to be consistent with the observed Universe by over 120 orders of magnitude. (That is, a factor of over 10120.)
In general, whenever you have two large numbers and you take the difference of them, you’re going to get another large number as well. For example, imagine the net worths of two random people on one of the world’s “billionaires” lists, person A and person B. Maybe person A is worth $3.8 billion and maybe person B is worth $1.6 billion, and therefore the difference between them would be ~$2.2 billion: a large number indeed. You can imagine a scenario where the two people you randomly picked are worth almost exactly the same amount, but these instances usually only occur when there’s some relationship between the two: like they cofounded the same company or happen to be identical twins with one another.
In general, if you have two numbers that are both large, “A” and “B,” then the difference between those numbers, |A – B|, is also going to be large. Only if there’s some sort of reason — an underlying symmetry, for example, or an underlying relationship between them, or some mechanism that’s responsible for those two numbers to nearly-perfectly match — will the difference between those numbers, |A – B|, turn out to be very small compared to “A” and “B” themselves.
The alternative explanation is that these two numbers really are very close together, but entirely coincidentally: something that’s more and more unlikely the closer these two values are to each other.
When we attempt to calculate, using quantum field theory, the expected value of the zero-point energy of empty space, the individual terms that contribute do so with values that are proportional to a combination of fundamental constants — √(ℏc/G) — raised to the fourth power. That combination of constants is also known as the Planck mass, and has a value that’s equivalent to ~1028 eV (electron-volts) of energy when you remember that E = mc². When you raise that value to the fourth power and keep it in terms of energy, you get a value of 10112 eV4, and you get that value distributed over some region of space.
Now, in our real Universe, we actually measure the dark energy density cosmologically: by inferring what value it needs to have in order to give the Universe its observed expansion properties. The equations that we use to describe the expanding Universe allow us to translate the “energy value” from above into an energy density (an energy value over a specific volume of space), which we can then compare to the actual, observed dark energy value. Instead of 10112 eV4, we get a value that’s more like 10-10 or 10-11 eV4, which corresponds to that mismatch of more than 120 orders of magnitude mentioned earlier.

For many decades, people have noted this property of the Universe: that our predicted value of the zero-point energy of space is nonsensical. If it were correct, the expanding Universe would have either recollapsed or expanded into empty nothingness extremely early on: before the electroweak symmetry broke and particles even received a non-zero rest mass, much less before atoms, nuclei, or even protons and neutrons could form. We knew that “prediction” must be wrong, but which of the following reasons explained why?
- The sum of all of these terms, even though they’re individually large, will somehow exactly cancel, and so the real value of the zero-point energy of space is truly zero.
- The actual value of the zero-point energy of space takes on all possible values, randomly, and then only in locations where its value admits our existence can we arise to observe it.
- Or this is a calculable entity, and if we could calculate it properly, we’d discover an almost-exact but only approximate cancellation, and hence the real value of the zero-point energy is small but non-zero.
Of these options, the first is just a hunch that can’t explain the actual dark energy in the Universe, while the second basically gives up on a scientific approach to the question. Regardless of the answer, we still need to rise to the challenge of figuring out how to calculate the actual zero-point energy of empty space itself.

If you’re a physicist, you might imagine that there’s some sort of miraculous cancellation of most of the possible contributions to the zero-point energy, but that a few contributions remained and do not have an equal-and-opposite contribution to cancel them out. Perhaps the contributions of all the quarks and antiquarks cancel. Perhaps the contributions of all the charged leptons (electron, muon, and tau) cancel with their antiparticle partners, and perhaps only the remaining, “uncanceled” contributions actually account for the dark energy that exists in the Universe.
If we imagine that there’s some sort of partial cancellation that occurs, what would we need to remain, left over, in order to explain the (relatively tiny) amount of dark energy that’s present in the Universe?
The answer is surprising: something that corresponds to an energy scale of only a fraction of an electron-volt, or somewhere between 0.001 and 0.01 eV. What sort of particles have a rest mass that’s the equivalent of that particular energy value? Believe it or not, we have some right here in the standard model: neutrinos.
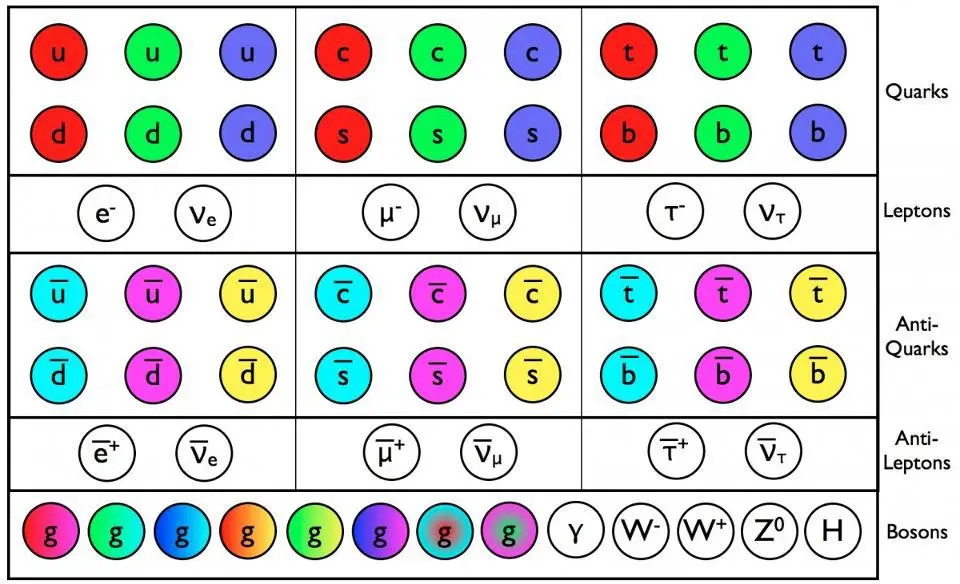
As originally formulated, the Standard Model would have all of the quarks be massive, along with the charged leptons, the W-and-Z bosons, and the Higgs boson. The other particles — neutrinos and antineutrinos, the photon, and the gluons — would all be massless. In the aftermath of the hot Big Bang, in addition to the normal matter particles (protons, neutrons, and electrons) that are produced, enormous numbers of neutrinos, antineutrinos, and photons are produced: about ~1 billion of them, each, for each and every proton that survives.
As it actually turns out, as we first suspected in the 1960s and then puzzled out in the 1990s and early 2000s, neutrinos aren’t massless at all. Rather, the species of neutrino or antineutrino (electron, muon, or tau) that’s produced, initially, isn’t always the species of neutrino you observe later on. Whether passing through the vacuum of space or whether passing through matter, neutrinos have a non-zero probability of changing their flavor, which can only occur if they have mass. (Otherwise, as massless particles, they wouldn’t experience time, and so would have no period-of-oscillation.) The fact that neutrinos have mass means, necessarily, that there’s some property about them that the original formulation of the Standard Model doesn’t account for.

Since we don’t know what, exactly, gives neutrinos these non-zero rest masses, we have to be very careful that we don’t prematurely rule out a scenario that connects their mass scales to the “energy scale” of the observed dark energy that appears in the Universe. Many have suggested plausible mechanisms for such a coupling, but no one has yet solved the hard problem of, “How do we calculate the zero-point energy of space using quantum field theory and the quantum fields that we know exist within our Universe?” We can measure the actual value of dark energy, but as far as understanding the theoretical side of the equation, we can only state, “We do not.”
Another aspect of the story that needs to be included is the fact that, prior to the start of the hot Big Bang, our Universe underwent a separate, earlier period where the Universe was expanding as though we had a positive, finite value to the zero-point energy of space: cosmological inflation. During inflation, however, the energy was much larger than the value it has today, but still not as large as the expected Planck-energy-range values. Instead, the energy scale of inflation is somewhere below ~1025 eV and could have potentially been as low as ~1014 eV: much much larger than today’s value but still much smaller than the value we would’ve naively expected.
Additionally, because there must be some sort of dark matter in the Universe — some particle that isn’t a part of the Standard Model — many have wondered if there couldn’t be some connection between whatever particle is responsible for dark matter with whatever energy scale is responsible for dark energy. One particle that’s a candidate for dark matter, the axion, typically comes in with very low masses that are below ~1 eV but that must be greater than about ~0.00001 eV (a micro-electron-volt), which places it right in the range where it would be very interestingly suggestive for a connection to dark energy.
But the hard problem still remains, and remains unsolved: how do we know, or calculate, what the zero-point energy of empty space actually is, according to our field theories?
That’s something we absolutely must learn how to do. We have to learn how to do this calculation, otherwise we don’t have a good theoretical understanding behind what is or isn’t causing dark energy. And the fact is we don’t know how to do it; we can only “assume it’s all zero” except for some non-zero part. Even when we do that, we have yet to discover why the “mass/energy scale” of dark energy takes on only this low-but-non-zero value any value seems possible. It must make us wonder: are we even looking at the problem correctly?
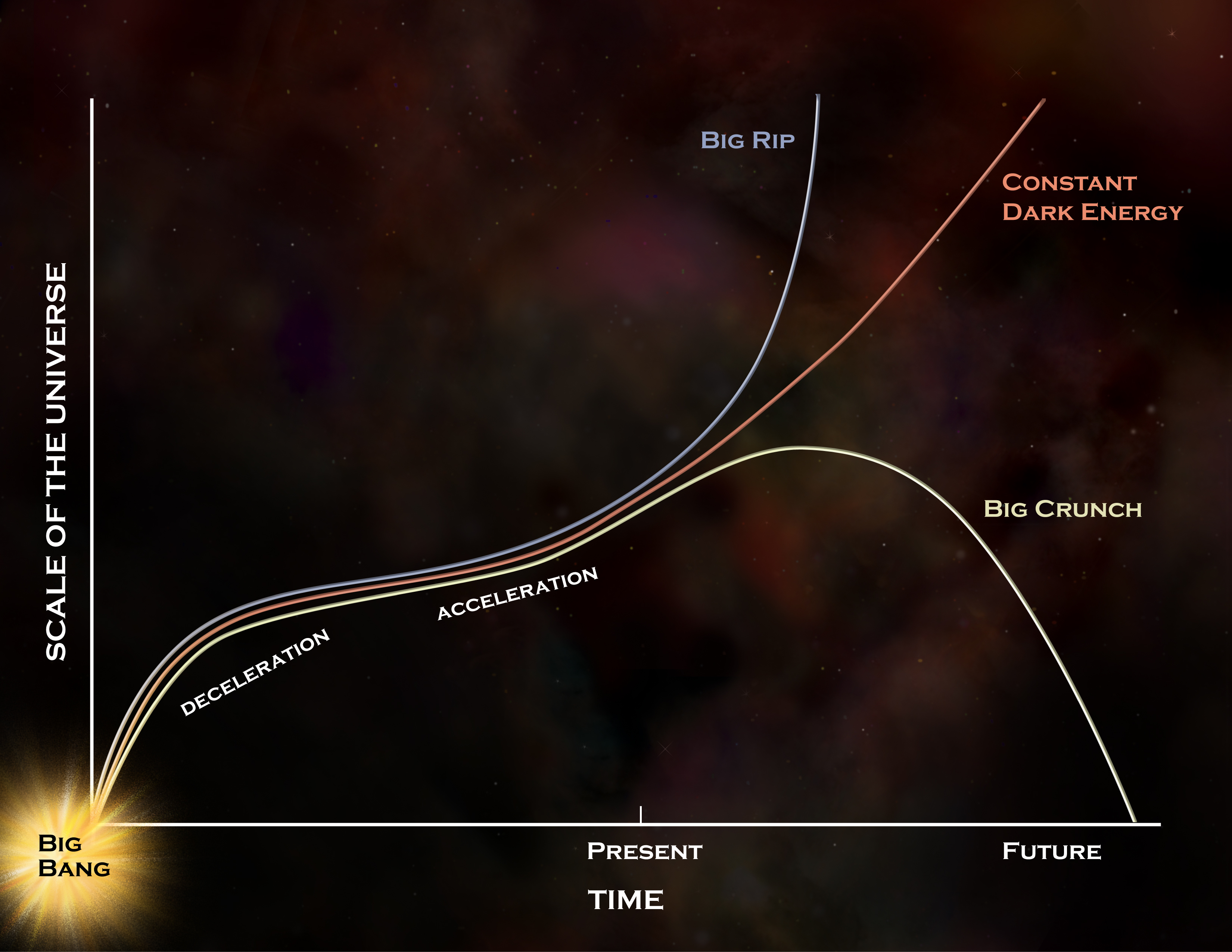
But there is a great set of reasons to be hopeful: observationally, we’re making tremendous progress. 20 years ago, we thought that dark energy behaves as the zero-point energy of empty space, but our uncertainties on it were something like ~50%. By 15 years ago, the uncertainties were down to about ~25%. Now, they’re down at around ~7%, and with upcoming missions such as ESA’s Euclid, the NSF’s ground-based Vera Rubin Observatory, and NASA’s upcoming Nancy Grace Roman Telescope scheduled to be our next flagship mission now that JWST has launched, we’re poised to constrain the equation-of-state of dark energy to within ~1%.
In addition, we’ll be able to measure whether the dark energy density has changed over cosmic time, or whether it’s been a constant over the past ~8+ billion years. Based on the data we have today, it’s looking like dark energy is very much behaving as a constant: at all times and locations, and that it’s consistent with being the zero-point energy of empty space itself. However, if dark energy behaves differently from this in any way, the next generation of observatories should reveal that as well, with consequences for how we perceive of the fate of our Universe. Even when theory doesn’t pave the way to the next great breakthrough, improved experiments and observations always offer an opportunity to show us the Universe as we’ve never seen it before, and show us what secrets we might be missing!