The Longest Walk On Earth Takes You From China to Liberia (or Vice Versa)
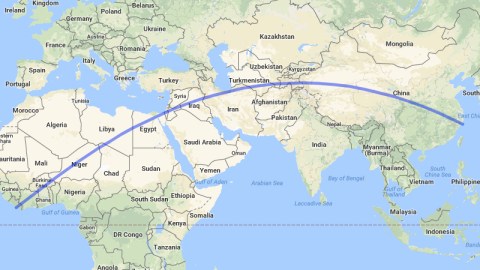
What is the longest straight line on Earth you can walk without getting your feet wet in a lake, sea or ocean? Someone has finally produced an answer to that question – and here’s the map that shows you how to go.
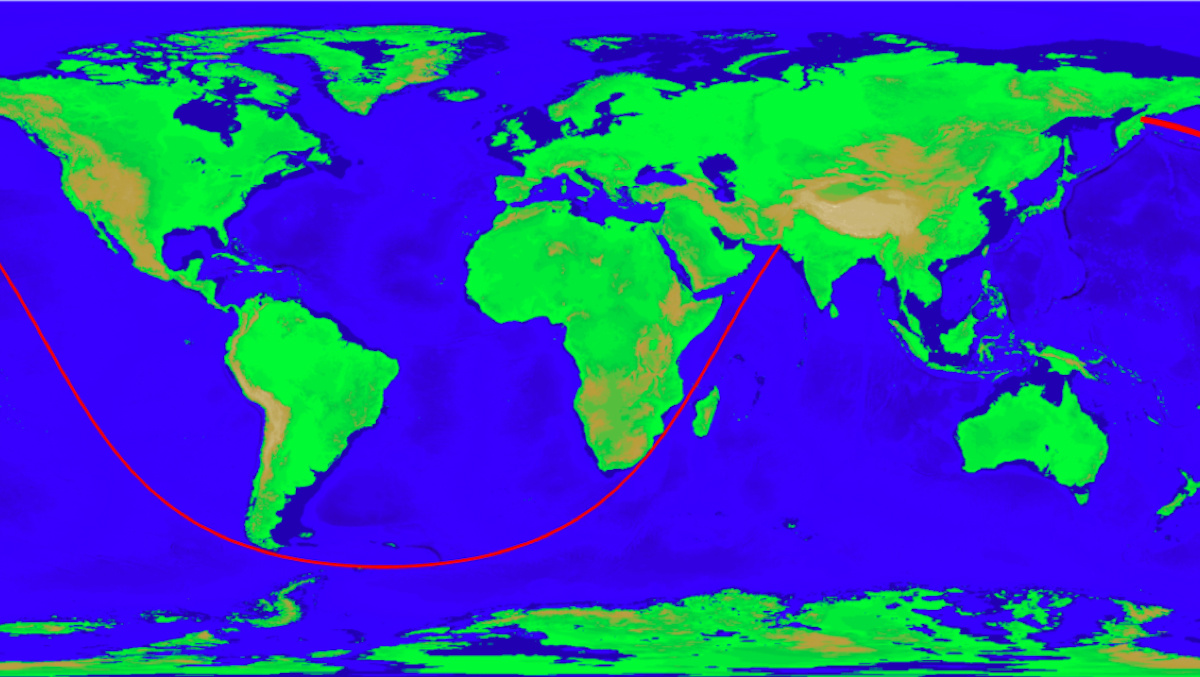
Start in Shitangzhen, a Chinese coastal city just south of Shanghai. March inland, and keep walking over the mountains and across the deserts of China’s Far East. Cross Central Asia into Iran, and narrowly avoid the Caspian Sea. Pass through Iraq, Jordan and Israel (watch out you don’t fall into the Mediterranean). Walk across the Sinai Desert, through the Nile Valley, and then onwards to the Sahara and Sahel. Finally arrive about 6 miles (10 km) north of Greenville, on Liberia’s Atlantic coast (1).

Congratulations: you have racked up 8,443 miles (13,589 km) – almost exactly one third of the total circumference of the planet (2).
If you’re wondering why that straight line looks bent, the clue is in the word circumference. In spite of the increasingly popular, yet demonstrably false theory that the Earth is flat (3), our planet is in fact almost perfectly round.
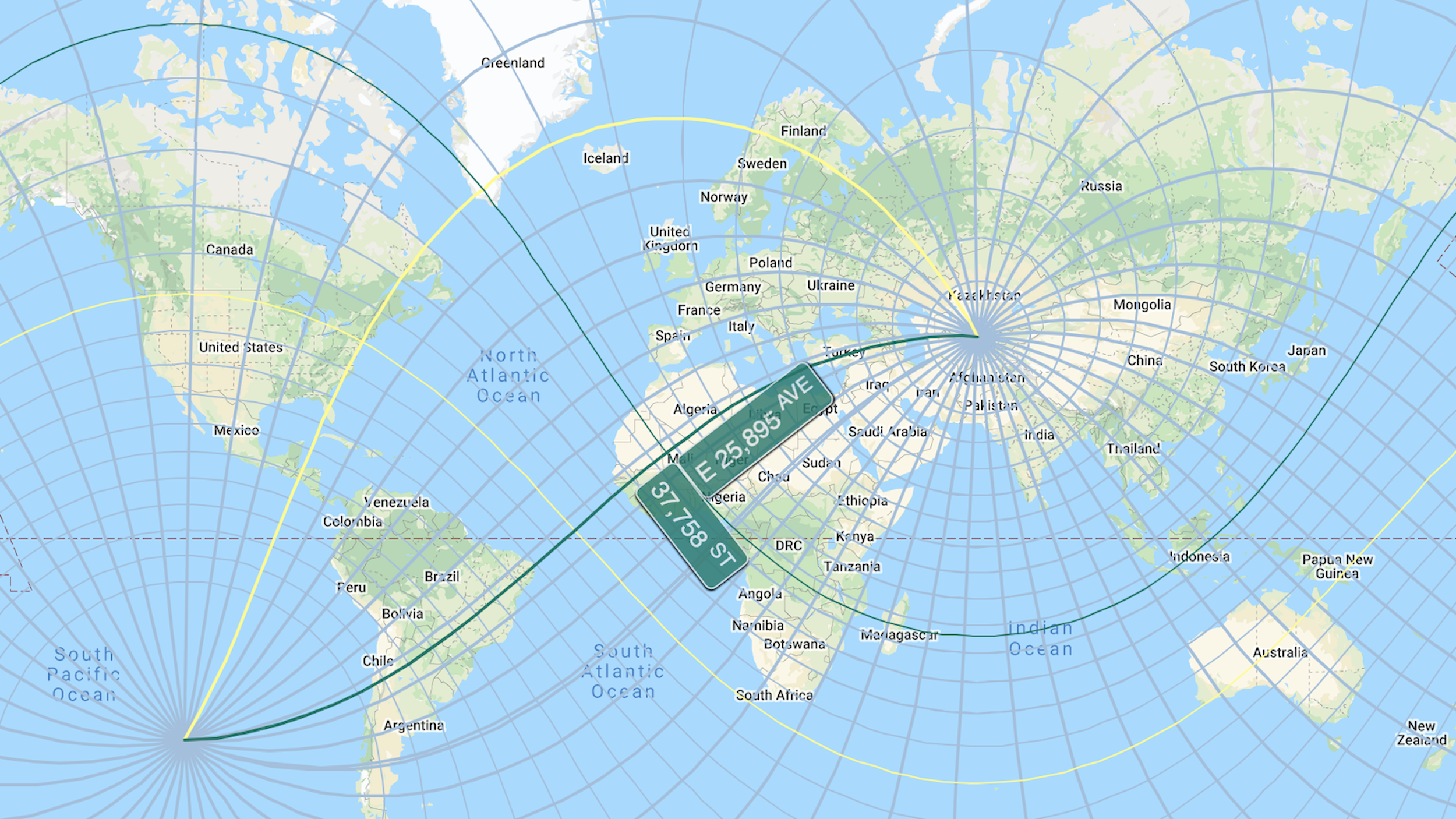
Which is why a straight line on the ground appears bendy on a map. Unless you adapt your map projection to protect the straightness of the line, like so:

Either way, it’s a pretty long schlep, and probably not soon to be attempted in real life, as the line transsects some of the world’s trouble spots as well as some of its most inhospitable zones. Maybe in a few years or so, at about the time when the hippie trail (2) reopens.
Maps found here at the personal page of IT/GIS consultant Guy Bruneau, via Simon Kuestenmacher. Map with caption here at That’s.
Strange Maps #856
Got a strange map? Let me know at[email protected].
(1) Or go the other way around, walking from Liberia to China. Same difference.
(2) About 24,874 miles (40,030 km) at the equator, but only 24,860 miles (40,008 km) from pole to pole. That is because the Earth is not a perfect sphere, but slightly flatter at the poles. Our planet, as geographers like to say, is an oblate spheroid.
(3) see #644.