The Universe is not symmetric

- During the 20th century, the recognition of certain symmetries in nature led to many theoretical and experimental breakthroughs in fundamental physics.
- However, the attempt to impose additional symmetries, while theoretically fascinating, led to an enormous series of predictions that weren’t borne out by experiment or observation.
- Today, many claim that theoretical physics has stagnated, as it’s clung to those unsupported ideas. We must face reality: the Universe is not symmetric.
When you wave at yourself in the mirror, your reflection waves back. But biologically, there are many ways it’s painfully obvious that your reflection is fundamentally different from you. When you raise your right hand, your reflection raises its left. If you looked at your body with X-rays, you’d find your heart is in the center-left of your chest, but for your reflection, it’s in the center-right. When you close one eye, your reflection closes its other eye. And while most of us are largely left-right symmetric, any apparent difference will manifest in the completely opposite fashion for our mirror-image counterpart.
You might think this is only a property of macroscopic objects made out of composites of fundamental entities, but as it turns out, the Universe is not symmetric at even a fundamental level. If you allow an unstable particle to decay, you’ll discover many fundamental differences between the allowable decays in the Universe and the decays you’d observe in the mirror. Certain particles, like neutrinos, only have left-handed versions, while their antimatter counterparts, the antineutrinos, only come in right-handed versions. There are electric charges whose motion creates currents and magnetic fields, but no magnetic charges whose motion creates magnetic currents and electric fields.
Despite the mathematical allure of additional symmetries, and some spectacular physical consequences they’d have for our Universe, nature itself is not symmetric. Here’s how physicists, after some initial successes invoking them, have been chasing after a grand possibility that simply isn’t borne out by reality.

Credit: Krea/Wikimedia Commons
At a very deep level, there’s an inextricable connection between symmetries in nature and conserved quantities in the Universe. This realization was mathematically proven over 100 years ago by Emmy Noether, whose eponymous theorem — Noether’s theorem — remains one of the bedrock principles of theoretical physics even to the present day. The theorem, originally only applicable to continuous and smooth symmetries over physical space, has since been generalized to uncover profound connections between symmetries of the Universe and conservation laws.
- If your system is time-translation invariant, which means it’s identical now to how it was in the past or will be in the future, then it leads to the law of conservation of energy.
- If your system is space-translation invariant, which means it’s identical here to how it was back over there or will be ahead down the road, then it leads to the law of conservation of momentum.
- If your system is rotationally invariant, which means you can spin it about its axis and its properties are identical, then it leads to the law of conservation of angular momentum.
Where these symmetries do not exist, neither do the associated conservation laws. For example, in the expanding Universe, time-translation invariance goes away, and so energy is not conserved under those circumstances.

Credit: Rob Knop
Although there are two types of symmetries — continuous symmetries like rotational or translational invariance, as well as discrete symmetries like mirror (reflection) symmetries or charge conjugation (replacing particles with their antiparticle counterparts) symmetries — not every symmetry that we can imagine is actually obeyed by the Universe.
For example, if you take an unstable particle like a meson and observe it, you’ll find that it has a spin: an intrinsic angular momentum to it. When that meson decays, the direction in which it “spits” a certain particle out will be correlated with its spin. If you picture it spinning clockwise, like curling the fingers of your left hand while your left thumb points towards your face, the particle that gets spit out will point in the direction of your thumb. The mirror-reflection version, however, will look right-handed instead of left-handed.
For some decays in some mesons, it’s a wash: there are equal numbers of right-handed and left-handed decays. But for others, the Universe somehow “prefers” one type of handedness over the other. The “mirror image” version of reality is fundamentally different from the reality that we observe.
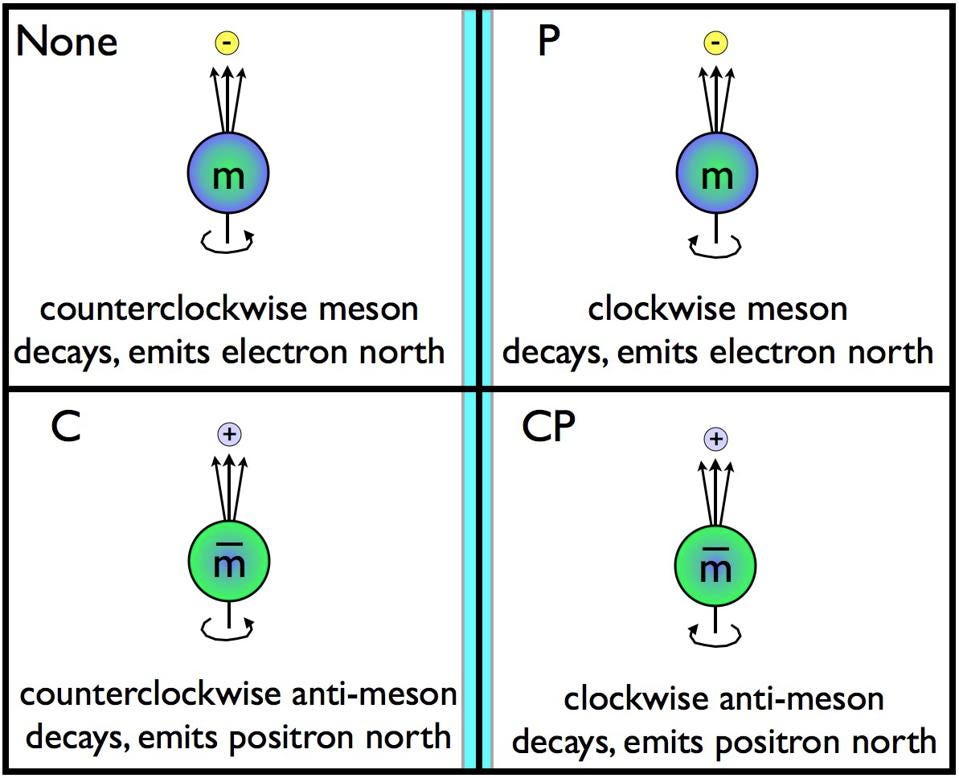
Credit: E. Siegel/Beyond the Galaxy
There are many, many other examples of these fundamental asymmetries in nature.
- When we observe neutrinos, we find that they’re always left-handed; if the neutrino moves in the direction that your thumb points, only the direction that your left hand’s fingers curl will describe the neutrino’s spin. Similarly, antineutrinos are always right-handed; it’s like there’s a fundamental difference between the matter and antimatter versions of these particles.
- When we observe the stars, galaxies, and even the intergalactic components of the Universe, we find that they’re overwhelmingly made of matter and not of antimatter. Somehow, in the Universe’s very distant past, a fundamental asymmetry between matter and antimatter was created.
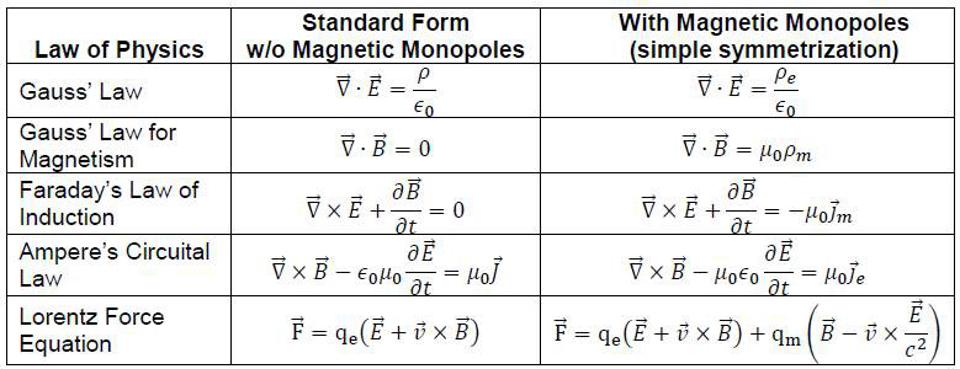
- And when we look at the laws of physics, we can see that it’s just as easy to write down the laws for magnetic charges and currents, and for the electric fields that they’d generate, as it is to write down the laws we know and have for electric charges and currents, which generate magnetic fields. But our Universe only seems to possess electric charges and currents, not magnetic ones. The Universe could have been symmetric, but for some reason, it is not.
Credit: Ed Murdock
Even so, the powerful connection between symmetries and conserved quantities led to a series of phenomenal developments in physics during the 20th century. There were realizations that symmetries could be restored at high temperatures, and when the Universe cools and those symmetries are broken, certain fascinating physical consequences would arise. Additionally, there were certain quantities that appeared to be conserved without explanation, and connecting those conserved quantities to a hypothetical underlying symmetry also bore some curious and revolutionary fruit in terms of what was at play in the Universe.
A quantum identity, the Ward identity, leads to the conservation of electric charge.
When certain symmetries break, a massless particle can pop out: a Goldstone boson.
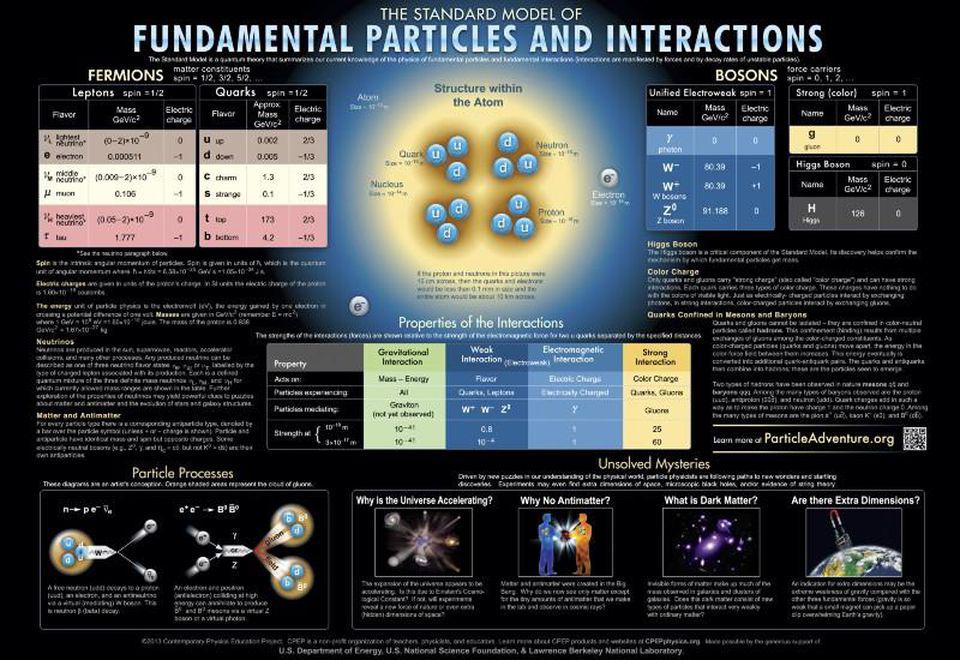
The application of group theory, Lie algebras, and other mathematical fields to the fundamental physics that underlies the Universe gave rise to a number of astonishing ideas. Perhaps the most revolutionary was the notion that two seemingly unrelated forces — the electromagnetic force and the weak nuclear force — could unify at some high energy. If this symmetry broke, then a series of new particles would come about, while other, previously massless particles would suddenly become very massive. The discovery of the superheavy weak gauge bosons, the W-and-Z bosons, as well as the massive Higgs boson, illustrated the spectacular success possible with imposing additional symmetries and the unification of forces.

Credit: Claire David
Given the unparalleled success of the Standard Model of particle physics in describing the Universe we inhabit, it’s only natural that physicists began to explore the idea of imposing additional symmetries and working out the consequences of what would arise if, at some even still-higher energies, there were an even more symmetric structure to reality.
Two of the most popular ideas were:
- imposing a left-right symmetry, where right-handed neutrinos/left-handed antineutrinos and magnetic charges (monopoles) were just as ubiquitous as left-handed neutrinos/right-handed antineutrinos and electric charges are today,
- and a unification symmetry, where the electroweak and strong forces unify at even higher temperatures than the electromagnetic and weak nuclear forces unify: at the grand unification scale rather than the electroweak scale.
The more symmetric the Universe is, the more simply you can describe it in mathematical terms. The idea behind this high-energy simplicity is that our Universe only appears as “messy” and “inelegant” as it does today because we exist at low energies, and these underlying symmetries are (badly) broken today. But in the hot, dense, energetic state of the early Universe, perhaps the Universe was more symmetric and simpler, and these additional symmetries would have fascinating physical consequences.
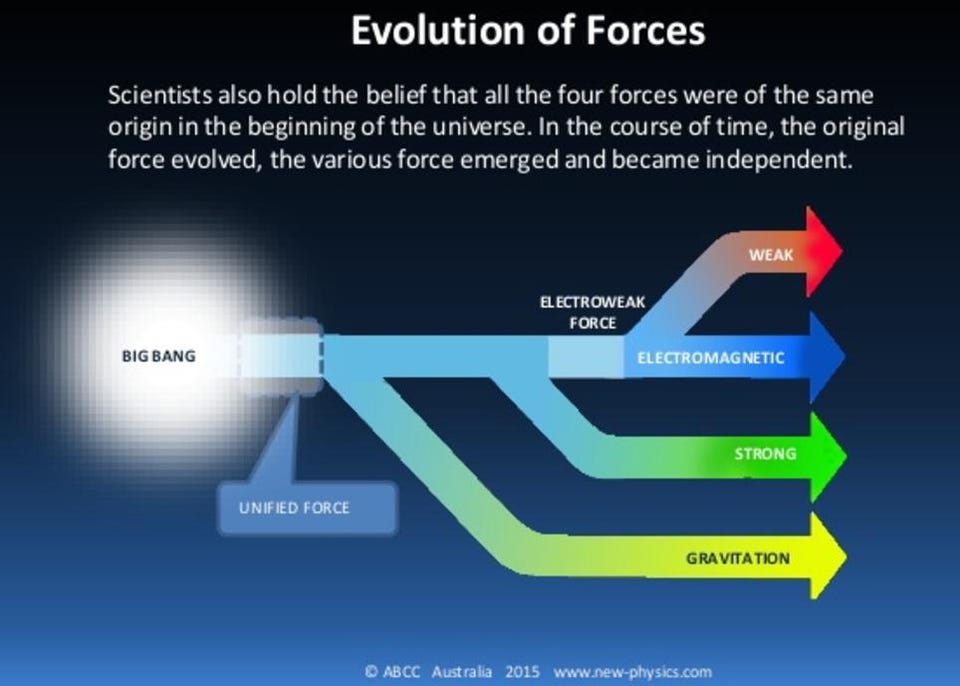
Credit: ABCC Australia, 2015
As soon as these ideas were considered, it became incredibly theoretically tempting to build a version of nature that was as symmetric, simple, and elegant as possible. Why stop at imposing left-right symmetries or with unifying the electroweak force with the strong nuclear force?
- You could impose an additional symmetry: one between Fermions (which are the fundamental particles with half-integer spin, i.e., ±1/2, ±3/2, ±5/2, etc.) and the Bosons (the fundamental particles with integer spin, i.e., 0, ±1, ±2, etc.) that would place them on identical footing. This idea leads to supersymmetry, one of the biggest ideas in modern fundamental physics.
- You could invoke larger mathematical groups to extend the Standard Model, leading to models that were both left-right symmetric and that unified the three quantum forces together.
- Or you could go even farther and attempt to fold gravity into the mix, unifying all of nature’s forces together into one enormous mathematical structure: the central idea of string theory.
The more symmetries you’re willing to impose, the simpler and more elegant the mathematical structure of the Universe appears to be.
Credit: Cjean42/Wikimedia Commons
But there are significant problems with adding in additional symmetries that are often glossed-over. For one, each of the new symmetries discussed here leads to the predictions of both new particles and new phenomena, none of which are borne out or validated by experiments.
- Making the Universe left-right symmetric leads to the prediction that magnetic monopoles ought to exist, and yet, we see no magnetic monopoles.
- Making the Universe left-right symmetric implies that both right-handed neutrinos and left-handed antineutrinos should both exist, and yet all neutrinos appear left-handed and all antineutrinos appear right-handed.
- Unifying the electroweak force with the strong nuclear force, in the framework of grand unification, leads to a prediction that new, super-heavy bosons should exist that couple to both quarks and leptons, enabling the proton to decay. And yet, the proton remains stable, with a lower limit to its lifetime in excess of a mind-boggling ~1034 years.
- And while that same grand unification framework offers a potential pathway for creating a matter-antimatter asymmetry where none had existed previously, the mechanism that it leads to has been invalidated by particle physics experiments.
Despite how compelling the scenarios for these additional symmetries are, they simply aren’t borne out by reality.
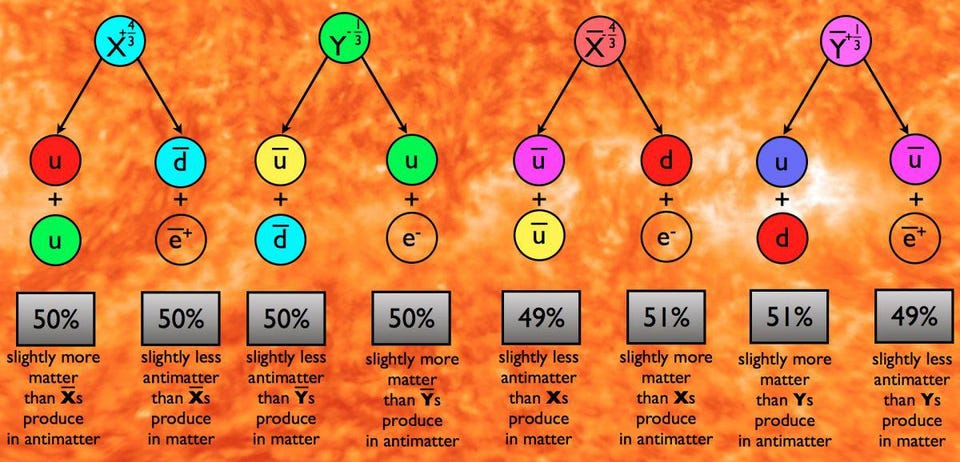
Credit: E. Siegel/Beyond the Galaxy
In fact, if you want to create a matter-antimatter asymmetry as large as we observe our Universe to possess today, you need a Universe that’s more asymmetric than the one we presently know of. Even with the asymmetries of the Standard Model, we can only arrive at a matter-antimatter asymmetry that’s millions of times smaller than we need to agree with observations. Additional symmetries can only help if they’re more badly broken, in some sense, than any other symmetries we have today.
It’s easy to argue that these “hints” of additional symmetries were put there by our own hopes, imaginations, and biases, not by a physical need for them. Some physicists have noted that the three coupling constants representing the three quantum forces — electromagnetism, the weak force, and the strong force — all change strength with energy, and that they almost (but not quite) all meet at the same high energy scale: around ~1016 GeV. If you add in some new particles or symmetries, like supersymmetry or extra dimensions, they might actually all meet.
But there is no guarantee this is how nature actually works; this is merely one mathematical possibility. (In fact, if you draw any three non-parallel lines, put them on a log-log scale, and zoom out, you’ll find that they all have this property.) And you must remember that, despite what Max Tegmark says, mathematics is not physics. Mathematics offers options to what physics could result in, but only by observing the Universe can you pick out which mathematical possibility has actual, physical relevance.
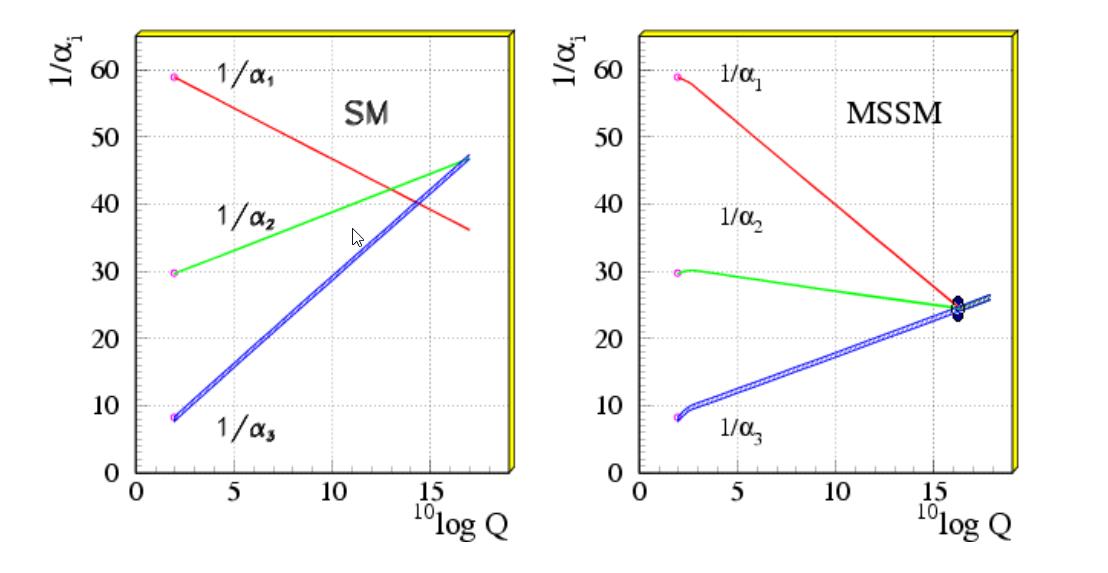
Credit: W.-M. Yao et al. (Particle Data Group), J. Phys. (2006)
There’s always a tremendous temptation, in any endeavor but especially in the sciences, to follow the pattern of what has worked before. If you don’t meet with immediate success, there’s a further temptation to imagine that those sought-after discoveries are just barely, just slightly out of reach, and that with a little more data just a little bit beyond the current frontiers, you’ll find what you’re seeking. But the lesson we should come away with, after more than 40 years of adding more and more symmetries beyond the ones we see in the Standard Model, is that there is no evidence supporting these ideas. No magnetic monopoles, no “other-chirality” neutrinos, no proton decay, etc.
The Universe is not symmetric, and the sooner we let our measured Universe, rather than our theoretical prejudices, be our guide, the better off we’ll all be. There are many alternative ideas to envisioning a more symmetric Universe, and perhaps it’s time for that mainstream but unsupported idea to give way to others if progress is to be made. As physicist Lee Smolin put it in a 2021 interview:
“For me, when people talk about diversity, that means not just women and blacks and aboriginals and who else, those are all very very important, but also very important are people who think differently… among the people who are excellent, technically, we want as wide a variety of ideas and viewpoints and types and personalities and gender and race… it’s yes yes yes yes. I would hope that the next generation and the second-to-next generation live in a scientific world that is much more fun. Because if everyone’s like you, it’s not fun.”