Has a new experiment just proven the quantum nature of gravity?

- Three of our fundamental forces of nature — the electromagnetic and strong and weak nuclear forces — are known to be quantum in nature.
- However, the oldest known fundamental force, gravity, has only been shown to exhibit behavior described by Einstein’s general relativity: a classical and continuous theory.
- By demonstrating that particles display the Aharonov-Bohm effect for gravitational forces, previously only seen with electromagnetic ones, we might have our first clue to gravity’s quantum nature.
If you were to break down the matter in our Universe to its smallest and most fundamental subatomic constituents, you’d find that everything was made up of individual quanta, each of which possesses both wave and particle properties simultaneously. If you pass one of these quantum particles through a double-slit and don’t observe which slit it passes through, the quantum will behave as a wave, interfering with itself on its journey and leaving us with only a probabilistic set of outcomes to describe its ultimate trajectory. Only by observing it can we determine precisely where it is at any moment in time.
This bizarre, indeterminate behavior has been thoroughly observed, studied, and characterized for three of our fundamental forces: the electromagnetic force and the strong and weak nuclear forces. However, it’s never been tested for gravitation, which remains the one remaining force that only has a classical description in the form of Einstein’s general relativity. Although many clever experiments have attempted to reveal whether a quantum description of gravity is required to account for the behavior of these fundamental particles, none has ever been performed decisively.
However, a long-studied quantum phenomenon, the Aharonov-Bohm effect, has just been discovered to occur for gravity as well as electromagnetism. A greatly underappreciated result, it could be our first clue that gravity is truly quantum in nature.

The quantum question
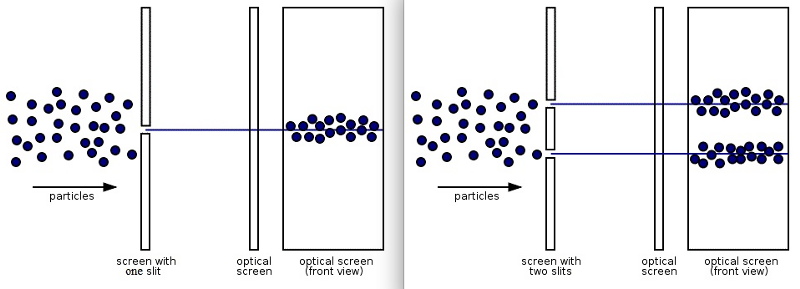
In the world of quantum physics, few experiments are more demonstrative of the bizarre nature of reality than the double-slit experiment. Originally performed with photons more than 200 years ago, shining light through two thin, closely-spaced slits resulted not in two illuminated images on the screen behind the slits, but rather in an interference pattern. The light that went through each of the two slits must be interacting before they reach the screen, creating a pattern that displays light’s inherent wave-like behavior.
Later on, this same interference pattern was shown to be generated with electrons as well as photons; for single photons, even as you passed them through the slits one at a time; and for single electrons, again even as you passed them through the slits one at a time. As long as you don’t measure which slit the quantum particles go through, the wave-like behavior is easily observable. It is evidence of the counterintuitive, but very real, quantum mechanical nature of the system: Somehow, an individual quantum is capable of going through “two slits at once” in a sense, where it must interfere with itself.

And yet, if you do measure which slit these quanta pass through, you see no interference pattern at all. Instead, you just get two “clumps” on the far side of the screen, which correspond to the set of quanta that went through slit #1 and slit #2, respectively.
This is an extraordinarily weird result that gets at the heart of what makes quantum physics so unusual, and yet, so powerful. You cannot simply ascribe definite quantities like a “position” and a “momentum” to each particle, as you would in a classical, pre-quantum treatment of those quantities. Instead, you have to treat position and momentum as quantum mechanical operators: mathematical functions that “operate” (or act) on a quantum wavefunction.
When you “operate” on a wavefunction, you get a probabilistic set of outcomes for what is possible to observe. When you actually make that key observation — i.e., when you cause the quantum you’re “observing” to interact with another quantum whose effects you then detect — you recover only a single value.
Let’s assume that you perform this experiment with electrons — particles with a fundamental, negative electric charge — and that you send them through these slits one at a time. If you measure which slit the electron goes through, it’s easy to describe the electric field generated by the electron as it goes through that slit. But even if you don’t make that critical measurement — even if the electron, so to speak, goes through both slits at once — you can still describe the electric field that it generates. The reason you can do this is because it isn’t just the individual particles or waves that are quantum in nature, but the physical fields that permeate all of space are quantum in nature as well: they obey the rules of quantum field theory.
For the electromagnetic interaction, as well as the strong and weak nuclear interactions, we’ve verified and validated the predictions of quantum field theory many times over. The agreement between theoretical predictions and the results of experiments, measurements, and observations is spectacular, agreeing in many cases to better than 1-part-in-a-billion precision.
However, if you ask a question like, “what happens to the gravitational field of an electron as it goes through a double slit,” you’re bound to be disappointed. Theoretically, without a working quantum theory of gravity, we cannot make a robust prediction, while experimentally, detecting such an effect goes far beyond our current capabilities. At present, we do not know whether gravity is an inherently quantum force or not, as no experiment or observation has been able to make such a critical measurement.
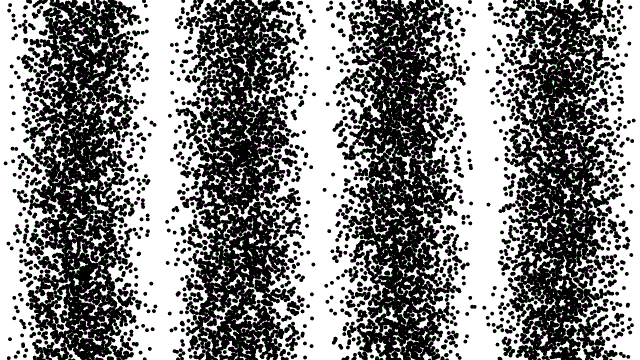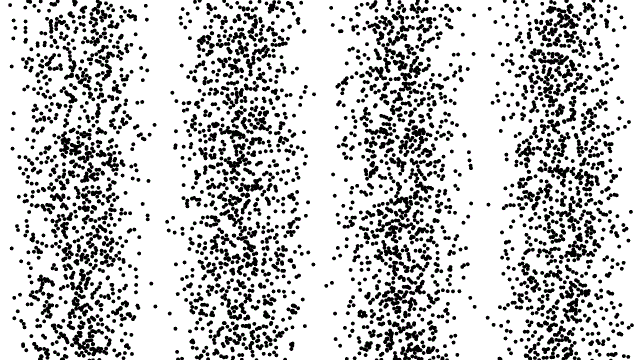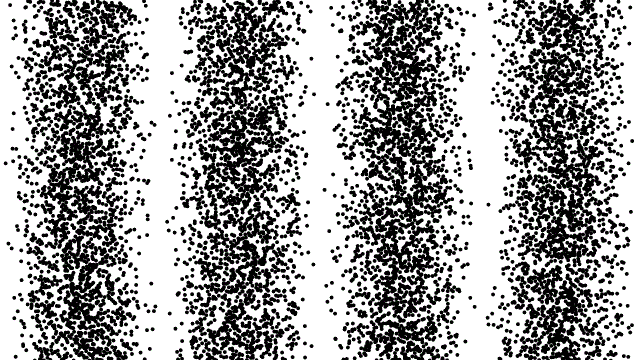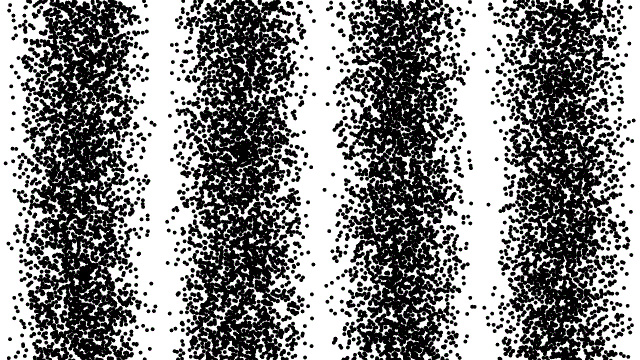
The Aharonov-Bohm effect
There are so many subtle quantum effects that not only pop out of our equations, but also have been physically verified that it’s sometimes difficult to keep track of them all. For example, in the classical Universe, if you have a charged particle in motion, it can be affected by both the presence of electric fields and magnetic fields.
- The electric field will accelerate the charged particle along the direction of the field, in direct proportion to the strength of the field and proportional to the charge of the particle, causing it to either speed up or slow down in the process.
- The magnetic field accelerates the charged particle perpendicular to both the magnetic field and the direction of motion of the particle, causing it to bend but not to increase or decrease its speed.
If your electric and magnetic fields are both zero, your electron won’t accelerate; it will just continue along in constant motion, exactly as you’d expect from Newton’s first law.
But in the quantum Universe, there’s another effect that comes into play that can change the behavior of your quantum particle, even when the electric and magnetic fields are both zero: the Aharonov-Bohm effect. The key to understanding it is to learn the relationship between electric and magnetic fields and a more abstract concept: electric and magnetic potential.

Electric potential is more commonly known as voltage. Changes in voltage, from one region to another, are what creates electric fields and compels electric currents to flow. You can get the electric field from the electric potential simply by taking the gradient, which details how the field changes, directionally, throughout space.
Magnetic potential is a little more complicated because it doesn’t have a common analog like voltage, and also because the magnetic field itself doesn’t come about from a simple gradient, but rather from a mathematical operation known as the curl of the magnetic potential.
Now, here’s where it gets interesting: You can have a non-zero electric and/or magnetic potential in a region even where the electric and magnetic fields are both zero. For a long time, physicists wondered whether the potential was actually a physical thing, since it appears to be the fields, not the potentials, that affects the motions of particles in a measurable way. This is true in classical physics, but not exclusively in quantum physics. In particular, the potential couples to the phase of a charged particle’s wavefunction, and if you measure the phase of that charged particle — which you typically do with interference experiments — you’ll find that it does depend on the electromagnetic potential, not just on the electric and magnetic fields.
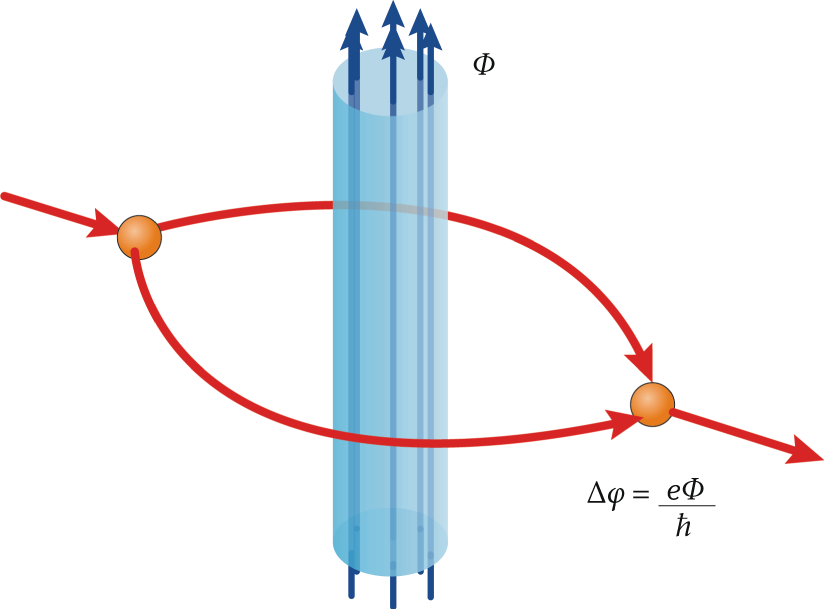
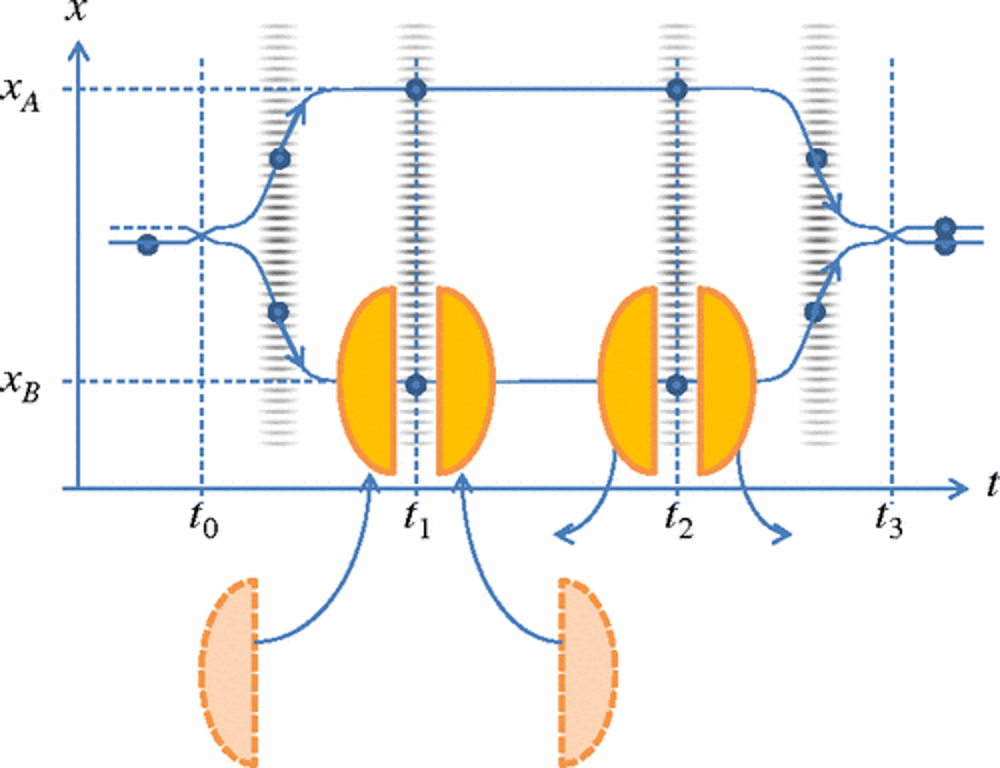
The way we typically measure the Aharonov-Bohm effect is to set up a cylindrical region of space that contains a substantial but highly confined magnetic field: something that’s easy to create with a long coil of wire, like a solenoid. You then set up a charged particle in motion around that magnetic field, but carefully, so that the particle itself doesn’t pass through the region containing the field.
The wavefunction will still experience a phase shift that can be — and has been — observed experimentally. This is true even though the electric and magnetic fields are negligible outside the confined region containing the field, and the probability of finding the particle within the field-containing region is also negligible.
It might seem like yesterday’s news. After all, the original work by Aharonov and Bohm dates back to 1959, with an earlier paper by Ehrenberg and Siday predicting the same effect back in 1949. However, the same effect that’s been observed for the magnetic potential should be observable for any force that arises as a consequence of a potential. This includes not only the electric force and the other known quantum forces, but also the gravitational force. If a clever enough setup could be devised, it should be possible to search for evidence of a gravitational Aharonov-Bohm effect as well.
What about gravity?
When you want to experiment with the gravitational force, the biggest problem is always that gravitational effects are so maddeningly small. Although people have been designing experiments for many decades with a view toward detecting this effect, an enormous breakthrough came in 2012. A team of researchers led by Michael Hohensee came up with the idea for an experiment that could feasibly be performed with current technology.
The idea was that you can create ultra-cold atoms and control their motion by pulsing a laser beam, including into a region where the gravitational potential — but not the field — is different from other locations. Even in regions where the gravitational force is zero, which can be arranged by a careful setup, the non-zero potential could still have an effect. If you can then split a single atom into two matter waves, move them into areas with different potentials, and then bring them back together, you could observe an interference pattern, measuring their phase and, therefore, quantifying the gravitational Aharonov-Bohm effect.
It’s a purely quantum phenomenon that we expect. But for the first time, it’s entirely dependent on the gravitational force, rather than any other interaction.
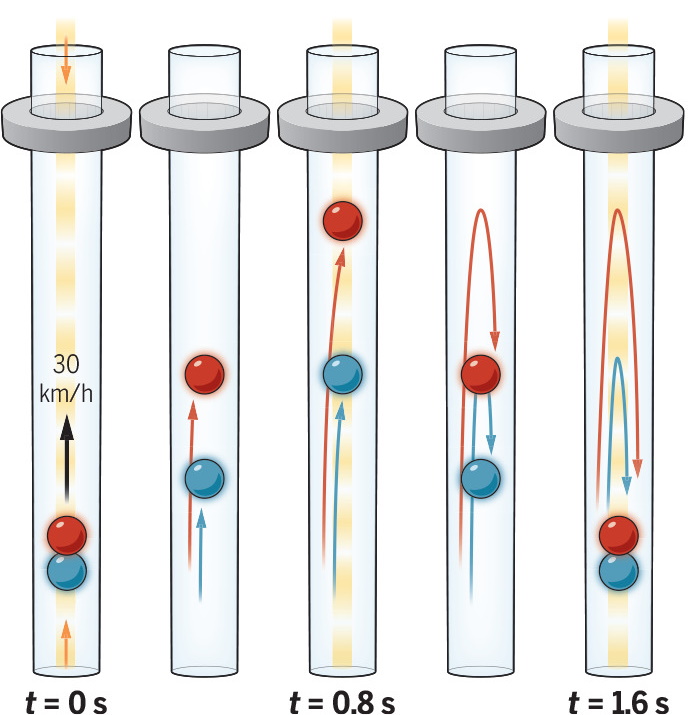
A decade later, a team led by Chris Overstreet has done it. As published in the January 13, 2022 issue of Science, the team took multiple ultra-cold rubidium atoms, put them into quantum superpositions with one another, and compelled them to trace two different paths inside a vertical vacuum chamber. Because there was a heavy mass at the top of the chamber — but one that was axially symmetric and completely outside of the chamber itself — it only changed the gravitational potential of the atoms, with the atom that reached a higher trajectory experiencing a greater change in potential.
Then, the atoms are brought back together, and from the interference pattern that is produced, a phase shift emerges. The amount of the phase shift that’s measured should correspond to:
- how separated the two atoms are from one another,
- how close they each come to the top of the chamber,
- and whether the external mass which alters the gravitational potential is present or not.
By performing this experiment over and over with a variety of such conditions, Overstreet’s team was able, for the first time, to measure the phase shifts of these atoms and compare them with the theoretical predictions for the gravitational Aharonov-Bohm effect. Lo and behold, not only has it been detected, but the match is dead on.
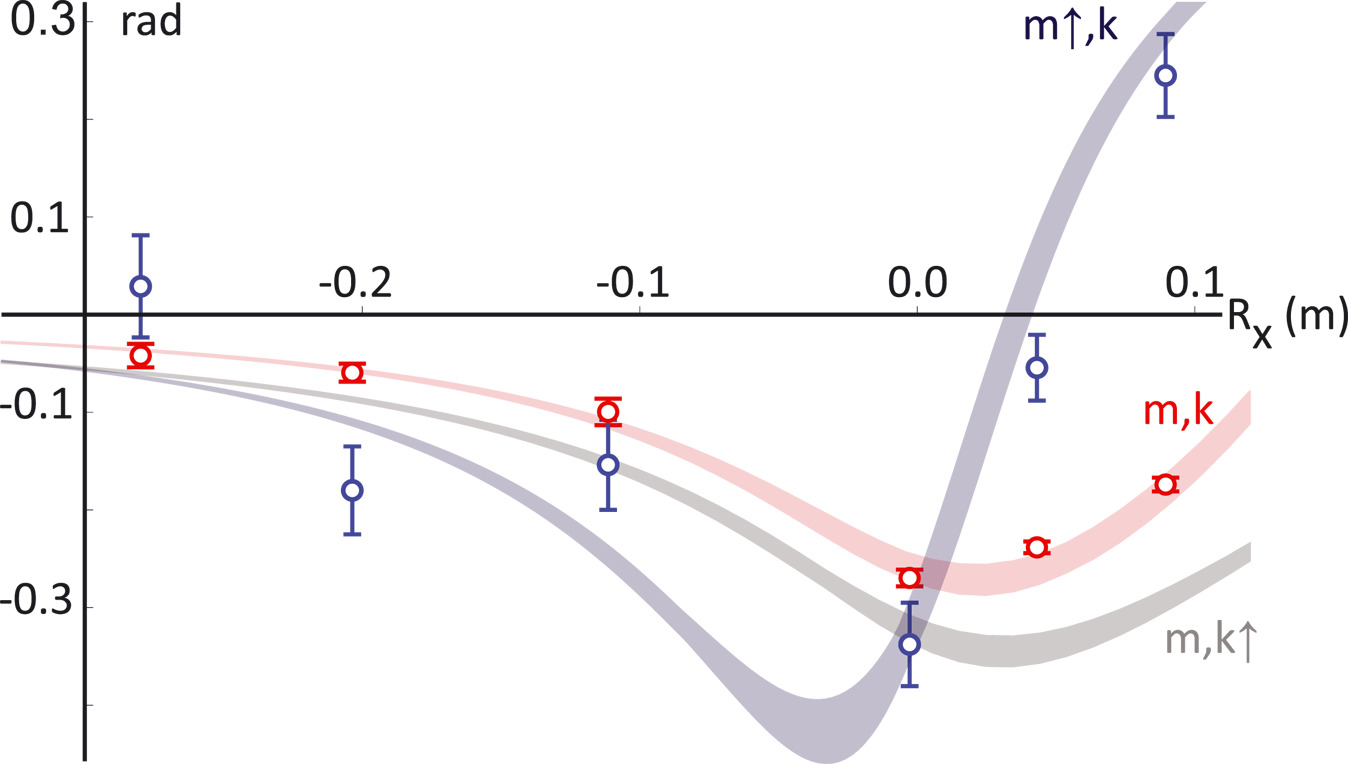
With that in mind, we come to the big question: Does the detection of this quantum mechanical phase shift, owing to the gravitational potential and not to either the gravitational field or any of the known quantum forces, demonstrate the inherently quantum nature of gravity?
Not to the point of this being a “proof,” unfortunately. We have created a phase shift, shown how the shift accumulates owing to gravitational potential and not the gravitational field, and measured it to be in agreement with theoretical predictions using atom interferometry. This establishes the same thing for gravitation that was previously established for electromagnetism: a demonstration that it isn’t simply the gravitational force or field that’s real, but that the gravitational potential itself has real, physical effects on the quantum mechanical properties of a system.
This is a remarkable achievement. But the analysis could be applied to any force or field that’s derivable from a potential: both quantum and classical. It’s a tremendous triumph for quantum mechanics under the influence of gravity, but it isn’t quite enough to demonstrate the quantum nature of gravity itself. Perhaps someday we’ll get there. In the meantime, the quest for a deeper understanding of gravitation itself continues.