How the unstable muon could revolutionize experimental particle physics
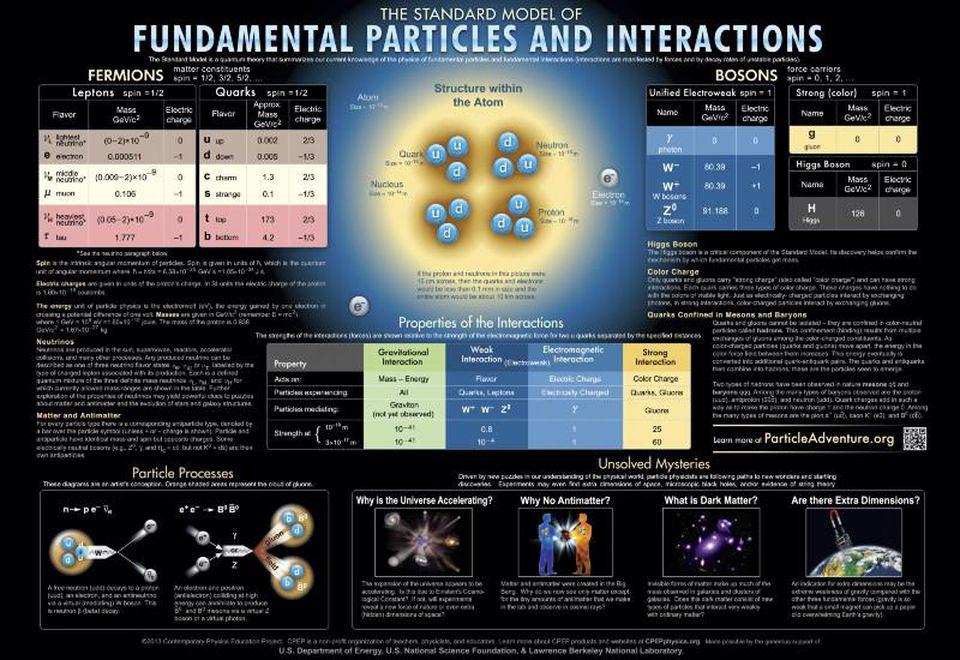
- When it comes to particle colliders, electrons and protons each have limitations based on their properties.
- Protons are composite particles, with energies divided among their components, while electrons are light, and emit radiation when you curve them in magnetic fields.
- The muon, despite its inherently small lifetime of just 2.2 microseconds, might offer the best of both worlds, revealing the Universe as neither protons nor electrons can.
If you want to uncover all the particles that fundamentally exist, your best bet is to smash particles together, under controlled laboratory conditions at extremely high energies. Whenever two particles collide, they have to conserve both energy and momentum, as well as other quantum properties that have associated conservation laws. However, there’s often a freedom that comes along with any particular collision: the freedom to create new particles. So long as all the relevant conservation laws are obeyed, the only limit for what you can create is set by Einstein’s most famous equation: E = mc2.
The more energy you have available for particle creation, the greater your potential to discover new, unstable, and massive particles. This very technique — of smashing particles together, building a detector around the collision point, measuring what comes out, and reconstructing what it was that we created — has been the hallmark of accelerator physics for more than a half-century. Traditionally, these collisions have involved either electrons or protons, as well as (sometimes) their antiparticles.
These are both great approaches, but they come with fundamental limitations. If we want to overcome them in some way, other than sheer brute force, a surprising candidate, the unstable muon, offers a possibility like no other. Here’s why.

How Particle Accelerators Work
At a very simple level, high-energy particle physics relies on two principles developed in the 1800s: how electric fields and magnetic fields affect charged particles.
- When you apply an electric field to a charged particle, it accelerates that particle along the direction of the electric field, adding to its kinetic energy in the process.
- When you apply a magnetic field to a charged particle, it accelerates that particle by keeping its speed the same, but changing its direction: perpendicular to both the magnetic field and the particle’s direction of motion.
Together, these principles allow you to build a particle accelerator in one of two ways. The first is the most straightforward: You can build a linear accelerator, where you start two particles at opposite ends of a long, straight track, accelerate them with electric fields, collimate them with magnetic fields, and cause them to collide at equal speeds, close to the speed of light, in opposite directions. A detector situated around the collision point can observe what comes out.

This method, however, is severely limited by both cost and engineering concerns. When I say you need a linear accelerator, I mean linear: You need it to go in a straight line. But the Earth is curved, and this becomes a very big problem for building something “straight” once you get to a size of more than a few kilometers.
For example, if you wanted to build a track that’s 20 km (about 12 mile) long, then the height difference between each tip of the accelerator and the center of the accelerator would only be ~8 meters, or about 26 feet. You can imagine either digging that deep underground or propping up the edges of the accelerator above ground without too much difficulty. That would give you ~10 km to accelerate each of your particles before they met in the middle, and however strong you could make your electric field would determine the energy of each particle.
But now let’s say you want to increase your energy to probe what you couldn’t probe previously. What would you do? To gain one order of magnitude of energy, you’d build an accelerator 10 times as long. Only, now instead of an offset of 8 meters (26 feet), you’d have an offset that’s 100 times larger: about 800 meters (2,600 feet), or around a half-mile. It’s for this reason that linear accelerators, for the most part, went out of fashion long ago.

Instead, our most powerful modern particle accelerators are built with a circular shape to them, rather than a linear one. The idea is as follows:
- there are “straight” portions of the track, and that’s where electric fields are applied, accelerating the particles in the forward direction and adding to their kinetic energies,
- along the “curved” portions of the track, magnetic fields are applied, bending the particles into a circular shape and changing their directions, without costing them any velocity or kinetic energy in the process.
As the particles inch ever closer to the ultimate speed limit, the speed of light, you have to intensify the magnetic fields to keep them bending in the same circle; a higher speed requires a stronger magnetic field to produce a circle of the same radius. In a very real sense, then, it’s simply the size of your particle accelerator and the strength of your magnetic field that primarily determine how energetic your particles can get.
In either case, all you have to do is magnetically “pinch” them together in the center of your detector and they’ll collide. As long as you can detect the properties of what comes out, you can reconstruct what happened at the collision point, giving you the ability to detect anything that you created, which, in turn, is only limited by the energy of the colliding particles and Einstein’s E = mc2.
The problem with electrons
Electrons, and their antiparticle counterpart, positrons, seem like the perfect candidate for this task. After all, they’re fundamental particles, and when you collide an electron and a positron together, they annihilate completely, leaving 100% of their particle energy available for the creation of new particles. Get an electron and a positron each up to 5 GeV (giga-electron-volts) of energy and you have 10 GeV of energy to produce new particles; get them up to 50 GeV apiece and you have 100 GeV for particle production; get them up to 500 GeV each and you have 1000 GeV, or 1 TeV (tera-electron-volts), of energy to make new particles.
But there’s a problem. The electric field part is easy; accelerate your electron (or positron) along the direction of an electric field and it simply gains energy and speed in that direction. But then, when you apply the magnetic field to bend the particle, the problem shows up: When charged particles travel in curved paths, they emit radiation.
How much radiation do they emit? Well, it’s proportional to the particles charge-to-mass ratio to the fourth power, which means a particle that’s 10 times heavier but the same charge as another will emit only 1/10,000th the amount of radiation as the original particle. The electron (and the positron) have the highest charge-to-mass ratios of any elementary or composite particle known, and that’s why any circular collider that leverages electron-positron collisions is fundamentally limited.

The problems with protons
“Okay,” you reason, “if electrons and positrons can’t get me up to the energies I want, I’ll just pick charged particles that are much more massive: like either protons and protons or protons and anti-protons.” This solves the problem that electrons and positrons had; you no longer get a large amount of that emitted radiation in your accelerator. But instead, you have two new problems to reckon with.
- The proton (and the anti-proton) aren’t fundamental particles, but are composite particles. They aren’t merely made up of three quarks (or anti-quarks) each, but also a mix of gluons and what we call “sea quarks,” which are the quark-antiquark pairs temporarily created in the interior of an atomic nucleus. You can reach very high energies with protons, but it’s not the whole protons that are colliding, but only one fundamental particle inside each proton, each containing only a sliver of the total energy in a proton.
- And yet, with each collision that occurs, you don’t get a clean signal, where all your detector “sees” is the output from the two fundamental particles that collided, but rather you get an enormous amount of debris, as every individual subatomic particle that was inside the proton can fly off and produce its own cascade of daughter particles.

Today, the Large Hadron Collider (LHC), is the most powerful particle accelerator in history, capable of reaching energies of 7 TeV per proton and colliding protons with protons around the various collision points where detectors have been built. What most people don’t remember is that before that enormous tunnel was used for colliding electrons with positrons. With protons instead of electrons and positrons, the LHC can achieve energies-per-particle some ~70 times greater than its predecessor, LEP (the Large Electron-Positron collider) could. Still, both methods are fundamentally limited, and if we want to discover what our current machines cannot, we only have three real options.
- We can build a large linear collider, suitable for colliding electrons and positrons. We’ll have to put the strongest electric field accelerators possible inside of them and build it as long as possible, and simply hope that something new shows up.
- We can build a much larger tunnel than presently exists at CERN, where the LHC is located. We can leverage that tunnel to conduct both electron-positron and proton-proton collision experiments, with the energies achievable limited by magnet strength and the size of the tunnel.
- We can turn to a fundamentally new method: building a muon/anti-muon collider. Although it faces challenges, it can overcome our current problems in a way that no collider has ever achieved before.

How the muon can save particle physics
Muons, in one sense, are exactly like electrons: They possess the same electric charge, they’re fundamental, and they behave as point particles. There are only two major differences between an electron and a muon: The muon is heavier, with 206 times the rest mass of the electron, and they’re unstable, with a mean lifetime of 2.2 microseconds before decaying into an electron and a pair of neutrinos.
However, this short lifetime is not prohibitive for using the muon (or its antiparticle counterpart, the anti-muon) in a particle physics experiment. Why not? Because of the physics of special relativity, and in particular, because of the property of time dilation.
A muon lives for ~2.2 microseconds when it’s at rest, but the closer it moves to the speed of light, the longer its effective lifetime is. With the same energies that we reach at the LHC, a muon’s effective lifetime would increase by a factor of ~66,000, meaning it could survive for more than a tenth of a second. So long as we can get muons and anti-muons circling in opposite directions within an accelerator ring, we could build a muon collider out of it.
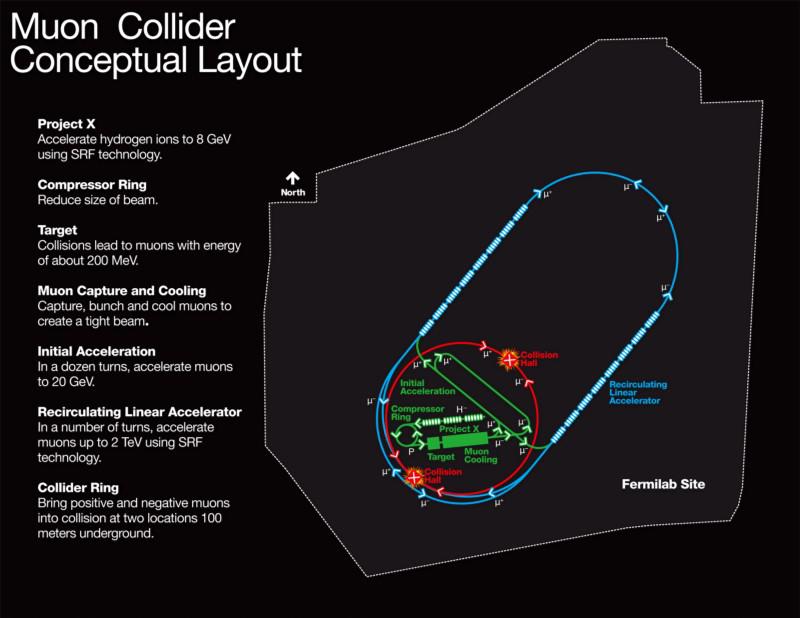
This, in principle, isn’t impossible. If you want to build a beam of muons, all you need to do is:
- accelerate protons up to high energies
- smash them into what we call a “fixed target,” which is basically a piece of acrylic
- where you produce a shower of particles, most of which are fast-moving, charged pions
- the pions will then decay, with ~99% of them decaying into even faster-moving muons (and anti-muons)
Finally, you gather and bend these muons into your accelerator ring, where you can collimate and speed them up further until you’re ready to collide them.
The reward is tremendous: clean collisions at high energies between point particles, where 100% of the particle energy is available for the creation of new particles via E = mc2, without any appreciable losses of energy due to synchrotron radiation. It’s the most straightforward way to get the best of both worlds, avoiding the problems inherent to the composite nature of the proton and avoiding the problems inherent to the high charge-to-mass ratios of electrons and positrons. Instead of simply building larger and larger accelerators, this novel approach, of a muon collider, could truly revolutionize the science of experimental particle physics.

However, there’s always a drawback. Because of the difficulty in gathering and collimating these fast-moving particles — the muons and anti-muons — the rate of collisions that occur inside a muon collider will be millions of times less frequent than in either an electron-positron or proton-proton collider. We might be able to generate greater amounts of energy than ever before for the creation of new particles, but, with current technology, it might take centuries or millennia to gather the necessary statistics to discover something novel.
Still, when it comes to considering the future of particle physics, the potential of the humble, unstable muon taking us well-beyond our current frontiers should not be underestimated. There are three things to consider when planning a new collider:
- the energies we’ll reach
- the cleanliness and efficiency of the post-collision signal
- the statistics of the total number of collisions we’ll be able to collect
Electron-positron colliders are good for #2 and #3, proton-proton colliders are good at #1 and #3, while muon-antimuon colliders are good for #1 and #2. Without knowing the solutions to cosmic mysteries like dark matter, dark energy, the hierarchy problem, and the origin of the matter-antimatter asymmetry, we are compelled to continue the cosmic search. As far as which method will be the most fruitful for solving these puzzles, only time, as well as future technology, will tell.