Why the cosmic speed limit is below the speed of light

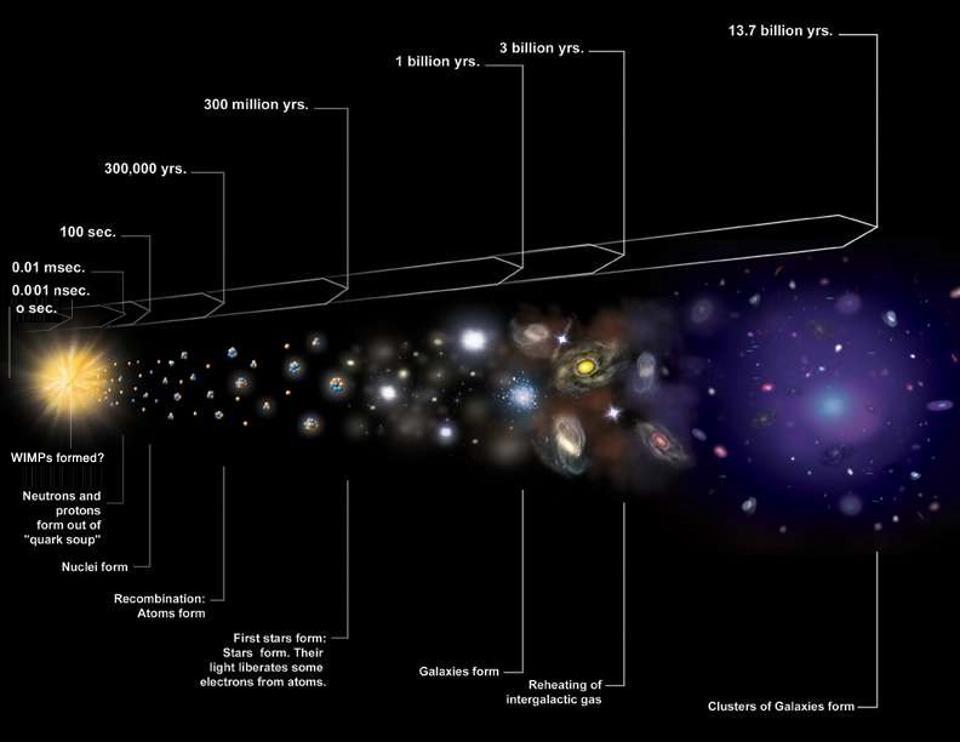
If you want to travel as fast as you can through the Universe, your best bet is to pump as much energy as possible into as small a mass as you can find. As you add progressively more kinetic energy and momentum to your particle, it will travel through space more quickly, approaching the ultimate cosmic speed limit: the speed of light. No matter how much energy you manage to add into the particle in question, you can only get it to approach the speed of light — it will never reach it. Since the total amount of energy in the Universe is finite, but the energy required for a massive particle to reach the speed of light is infinite, it can never get there.

But in our real-life Universe — not the idealized “toy” version we play with in our heads — we don’t simply have arbitrary amounts of energy to give to particles, and we also have to accept that they’re traveling through the space that actually exists, rather than what we imagine as a complete, perfect vacuum. While the Universe is capable of imparting far more energy to particles through natural accelerators — like neutron stars and black holes — than we can ever give them on Earth, even at state-of-the-art machines like CERN’s Large Hadron Collider, the fact that “the vacuum of space” isn’t a perfect vacuum is far more limiting than we often care to admit. Rather than the speed of light, the actual speed limit of particles is below that: set by what we call the GZK cutoff. Here’s what truly limits our motion through space.

Any cosmic particle that travels through the Universe, regardless of speed or energy, must contend with the existence of the particles left over from the Big Bang. While we normally focus on the normal matter that exists, made of protons, neutrons, and electrons, they are outnumbered more than a billion-to-one by the remnant photons and neutrinos. (Credit: NASA/Sonoma State University/Aurore Simmonet)

There are two facts that, when taken together, teach us that reality is not as simple as Newton intuited. Those facts are:

1. The particles that rapidly travel through the Universe are largely protons, electrons, heavier atomic nuclei, and occasionally positrons or anti-protons. All of these particles, detectable here on Earth and in space as cosmic rays, are electrically charged.
2. Light, which exists from many different sources, including stars, galaxies, and even the Big Bang itself, is an electromagnetic wave, and can easily interact with charged particles.

While even today’s modern physicists often automatically default to Newtonian-like thinking, we have to be careful to think of things as mere masses moving through the Universe, accelerated only by the forces that other particles and fields exert on them. Instead, we have to remember that the Universe is composed of physical quanta: individual energy packets with properties of both wave and particle, and that those quanta, unless somehow specifically forbidden from doing so, will always interact with one another.

A combination of X-ray, optical, and infrared data reveal the central pulsar at the core of the Crab Nebula, including the winds and outflows that the pulsars care in the surrounding matter. Pulsars are known emitters of cosmic rays, but the rays themselves don’t simply travel unimpeded through the vacuum of space. Space is not a perfect vacuum, and particles traveling through it must reckon with everything they encounter. (Credit: X-ray: NASA/CXC/SAO; Optical: NASA/STScI; Infrared: NASA/JPL-Caltech)

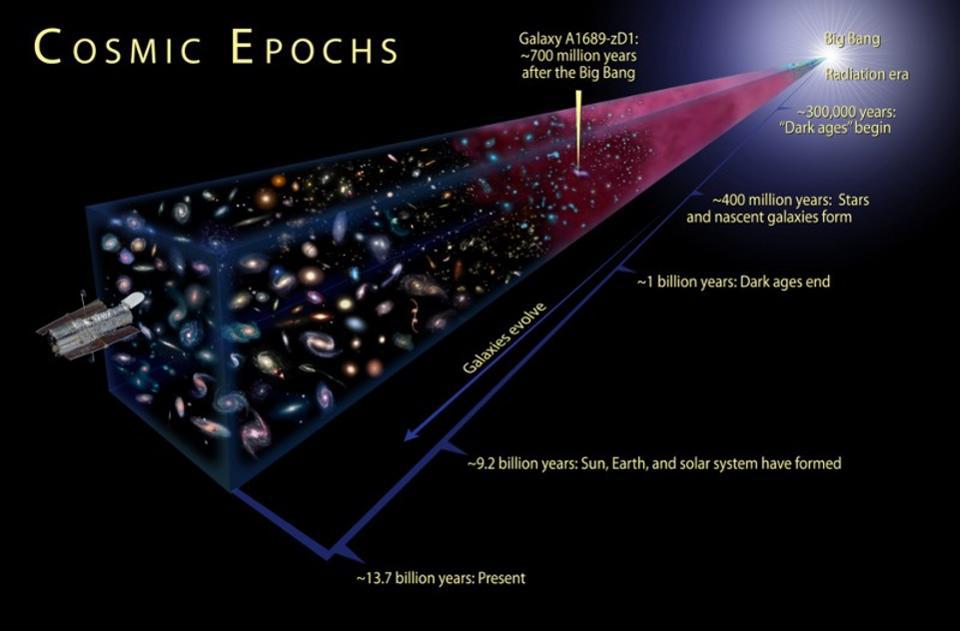
There are plenty of things left over from the Big Bang, including:

• stars
• gas
• dust
• planets
• stellar corpses

However, all of the items we just listed only compose about 2 to 2.5% of the total energy budget of what’s present in the Universe: only about half of the normal matter. There’s also dark matter, dark energy, neutrinos, photons, and a sparse, tenuous, ionized plasma present in space, with the last being known as the WHIM: the warm-hot intergalactic medium.

However, the biggest hinderance to charged particles traveling freely through the Universe is actually the least energetic component of all of these: the photons, or leftover particles of light from the Big Bang. While starlight is copious within an individual galaxy, there are places in the Universe — such as the remote depths of intergalactic space — where the only substantial quanta present are the photons left over from the Big Bang: the cosmic microwave background radiation, or CMB. Even today, in our Universe that’s expanded and cooled to be 46.1 billion light-years in radius, there are still around 411 CMB photons per cubic centimeter of space, with an average temperature of 2.7 K.

When cosmic particles travel through intergalactic space, they cannot avoid the leftover photons from the Big Bang: the cosmic microwave background. Once the energy from cosmic particle/photon collisions exceed a certain threshold, the cosmic particles will begin to lose energy as a function of the energy in the center-of-momentum frame. (Credit: Earth: NASA/BlueEarth; Milky Way: ESO/S. Brunier; CMB: NASA/WMAP)

Now, let’s imagine that we’ve got a natural particle accelerator like a neutron star or a black hole, creating electric and magnetic fields that are unheard of on Earth. In these extreme environments, millions of times the mass of Earth exists in a volume of space no larger than a few kilometers in diameter. These astrophysical locations often can achieve field strengths that are millions, billions, or even trillions of times in excess of the strongest electromagnetic fields ever generated in laboratories on Earth.

Any particle accelerated by these objects will be sent on an ultra-relativistic journey through the Universe, where it will inevitably encounter all sorts of particles. But it will particularly run into the most numerous of all particles: the CMB photons that are present. With around ~10⁸⁹ CMB photons filling our observable Universe, they’re the most abundant and evenly distributed type of quanta present in our cosmos. Importantly, there’s always a probability for a charged particle and a photon, regardless of what the relative energies of the particle and the photon are, to interact.

In this artistic rendering, a blazar is accelerating protons that produce pions, which produce neutrinos and gamma rays. Photons are also produced. Processes such as this may be responsible for the generation of the highest-energy cosmic particles of all, but they inevitably interact with the leftover photons from the Big Bang. (Credit: IceCube collaboration/NASA)

If there were no other particles — if we could activate our “toy” vision of an empty Universe where particles simply traveled unimpeded in a straight line until they reached their destination — we could imagine that only the field strengths of these astrophysical environments would place a cap on the total amount of energy a particle could possess. Apply a strong electric field in the direction it’s moving, and it’ll go faster and become more energetic.

In fact, you’d expect there wouldn’t be a limit at all. If this were how the Universe worked, you’d expect there’d be some sort of energy distribution of particles: where large numbers of particles had low energies and a few outlier particles had higher energies. As you looked to higher and higher energies, you’d keep finding particles, but they’d be fewer in number. The slope of the line might change as various physical processes became important at certain energies, but you wouldn’t expect particles to simply stop existing at some energy; you’d just expect there to be fewer and fewer of them until you reached the limit of what you can detect.

Illustration of an array of ground-based detectors to characterize a cosmic ray shower. When high-energy cosmic particles strike the atmosphere, they produce a cascade of particles. By building a large array of detectors on the ground, we can capture them all and infer the original particle’s properties. (Credit: ASPERA/G.Toma/A.Saftoiu)

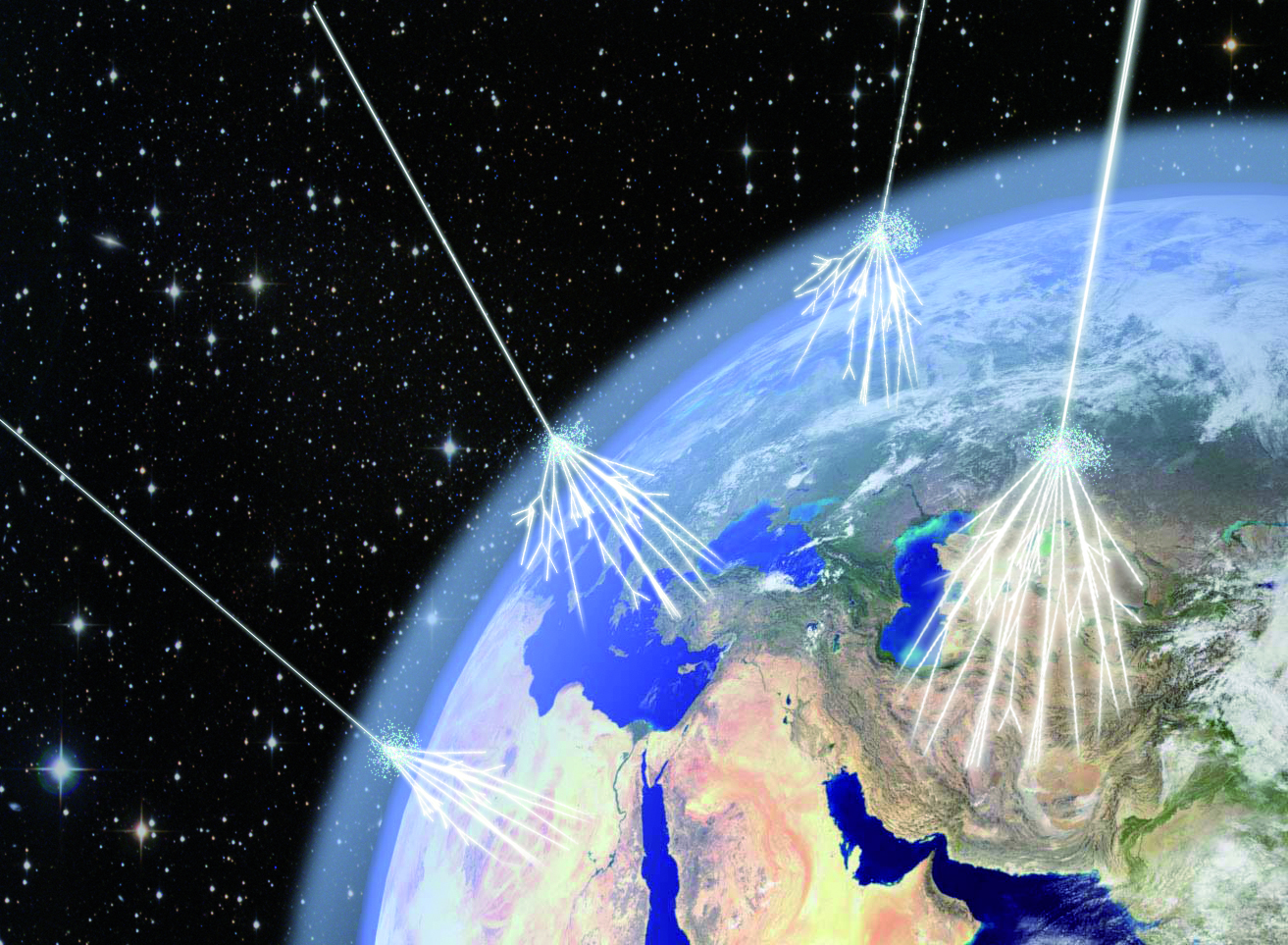
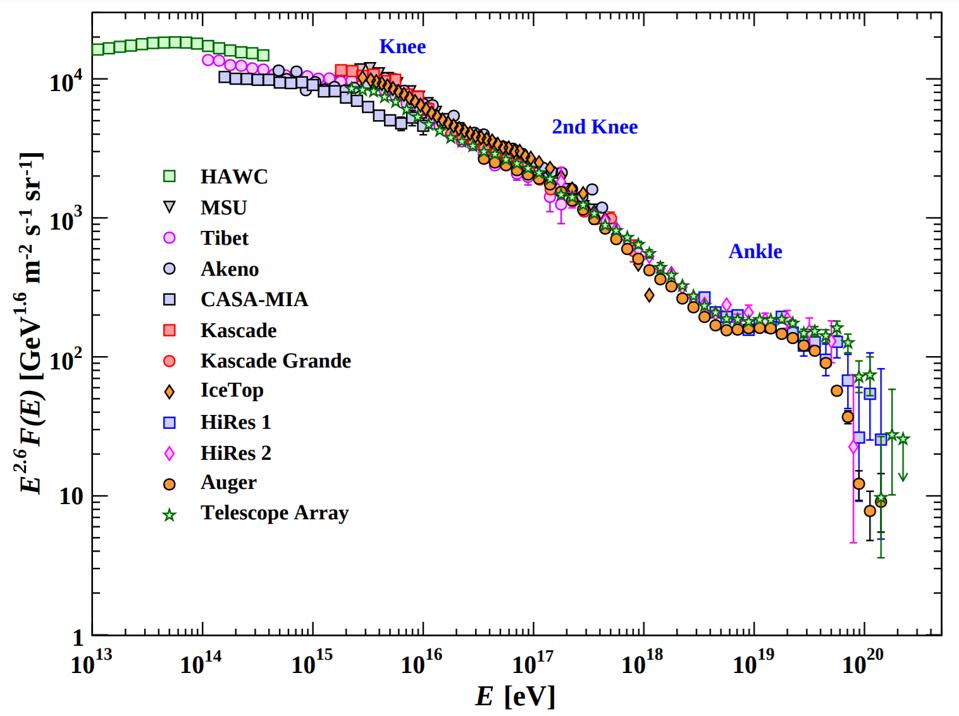
Today, our best modern cosmic ray observatories include large ground-based detectors that grab two main signals:

1. Particle showers, identifiable through an array of large-area detectors, such as those leveraged at the Pierre Auger Observatory
2. Cherenkov radiation detectors, which grab the characteristic glow of “blue light” (and also ultraviolet light) produced by fast-moving particles that exceed the speed of light in the medium of air, such as the HAWC telescope

At the top of the atmosphere, cosmic ray particles slam into ions, molecules, and atoms at the edge of the Earth. Through a series of chain reactions, they produce what we call “daughter particles” that are all, in some sense, direct descendants of the cosmic rays that initially impacted us. When we detect enough of the daughter particles (their descendants, in other words) that make it down to Earth’s surface, we can reconstruct the initial energies and properties of the cosmic rays that struck us.

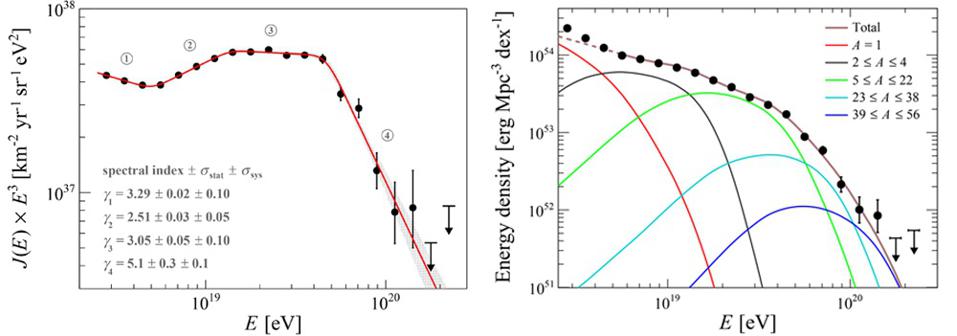
While we do, in fact, notice that there are much greater numbers of lower-energy particles than higher-energy ones, and that there are “kinks” in the graph where certain astrophysical phenomena suddenly become important, there also seems to be a cutoff: a point where no particles are seen to exist above a certain energy.

The energy spectrum of the highest energy cosmic rays, by the collaborations that detected them. The results are all incredibly highly consistent from experiment to experiment, and reveal a significant drop-off at the GZK threshold of ~5 x 10^19 eV. Still, many such cosmic rays exceed this energy threshold, indicating that this picture is not complete. (Credit: M. Tanabashi et al. (Particle Data Group), Phys. Rev. D, 2019)

What could cause this cutoff to exist?

This is where the idea of the cosmic microwave background comes into play. Remember: Light is an electromagnetic wave, and it interacts with charged particles. At low energies, this is simply Thomson or Compton scattering: where the charged particle and the photon exchange energy and momentum, but very little else occurs. Importantly, this is an extremely inefficient way of stealing energy from a fast-moving particle, even at high energies.

But once your particle hits a certain energy — which, for protons, the overwhelmingly most common type of cosmic ray, is ~10¹⁷ electron-volts — the photons appear energetic enough to the cosmic particle that they sometimes behave as though they’re actually made of electron-positron pairs. In the center-of-momentum frame, the proton perceives the photon as having a little over 1 Mega-electron-volts of energy, boosted from its typical CMB value of ~200 micro-electron-volts. Importantly, this is enough energy to produce, via Einstein’s famous E = mc², an electron-positron pair.

Once cosmic rays, like protons, start colliding with electrons and positrons instead of just photons, they shed energy much more rapidly. With each collision between a cosmic ray and an electron or positron, the original cosmic ray loses about 0.1% of its original energy.

Although many interactions are possible between charged particles and photons, at sufficiently high energies, those photons can behave as electron-positron pairs, which can drain a charged particle’s energy far more efficiently than simple scattering with mere photons. (Credit: Douglas M. Gingrich/University of Alberta)

Even over the millions or billions of light-years that cosmic particles travel, however, this shouldn’t be enough to place a hard cap on the total energy that particles possess; it should simply lower the detected abundance of particles above ~10¹⁷ eV in energy. However, there should be a cap, and that’s set by whenever the center-of-momentum energy rises high enough that a much more energetic particle can be created via E = mc²: the pion. In particular, the neutral pion (π⁰), which requires ~135 Mega-electron-volts of energy to create, will drain each cosmic ray proton’s energy by about 20%.

For any proton, therefore, that exceeds a critical energy threshold for creating neutral pions, there should only be a short amount of time it should be allowed to exist before interactions with CMB photons drag it down below that energy cutoff.

• For protons, that limiting energy is ~5 × 10¹⁹ electron-volts.
• The cutoff of that energy value is known as the GZK cutoff after the three scientists who first calculated and predicted it: Kenneth Greisen, Georgiy Zatsepin, and Vadim Kuzmin.

The event rate of high-energy cosmic rays versus their detected energy. If the pion-production threshold by CMB photons colliding with protons were a bona fide limit, there would be a “cliff” in the data to the right of the point labeled “372.” The existence of these extreme cosmic rays indicates that something else must be amiss. (Credit: Pierre Auger Collaboration, Phys. Rev. Lett., 2020)

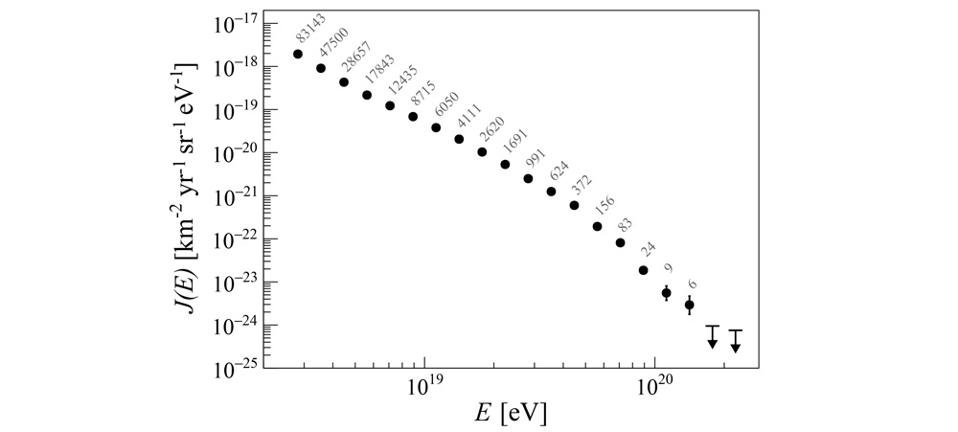
And yet, when we compare the predicted value of where this energy cutoff should be with where the energy cutoff is actually observed, we get a surprise.

Although there’s an extremely severe drop in the number of cosmic rays recorded above that expected cutoff, there have been hundreds of events confirmed to exceed that energy. In fact, they go up to a maximum observed energy of ~5 × 10²⁰ electron-volts — approximately 10 times the expected “maximum” value. Moreover, they’re not correlated with suspected nearby sources, like identified neutron stars or supermassive black holes, nor are they clumped or clustered together. They appear to come from random directions, but with energies that exceed the expected maximum limit.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

How is this possible? Does this mean the Universe is “broken” in some way?

Cosmic ray spectrum of the various atomic nuclei found among them. Of all the cosmic rays that exist, 99% of them are atomic nuclei. Of the atomic nuclei, approximately 90% are hydrogen, 9% are helium, and ~1%, combined, is everything else. Iron, the rarest of atomic nuclei, may compose the highest-energy cosmic rays of all. (Credit: M. Tanabashi et al. (Particle Data Group), Phys. Rev. D, 2019)

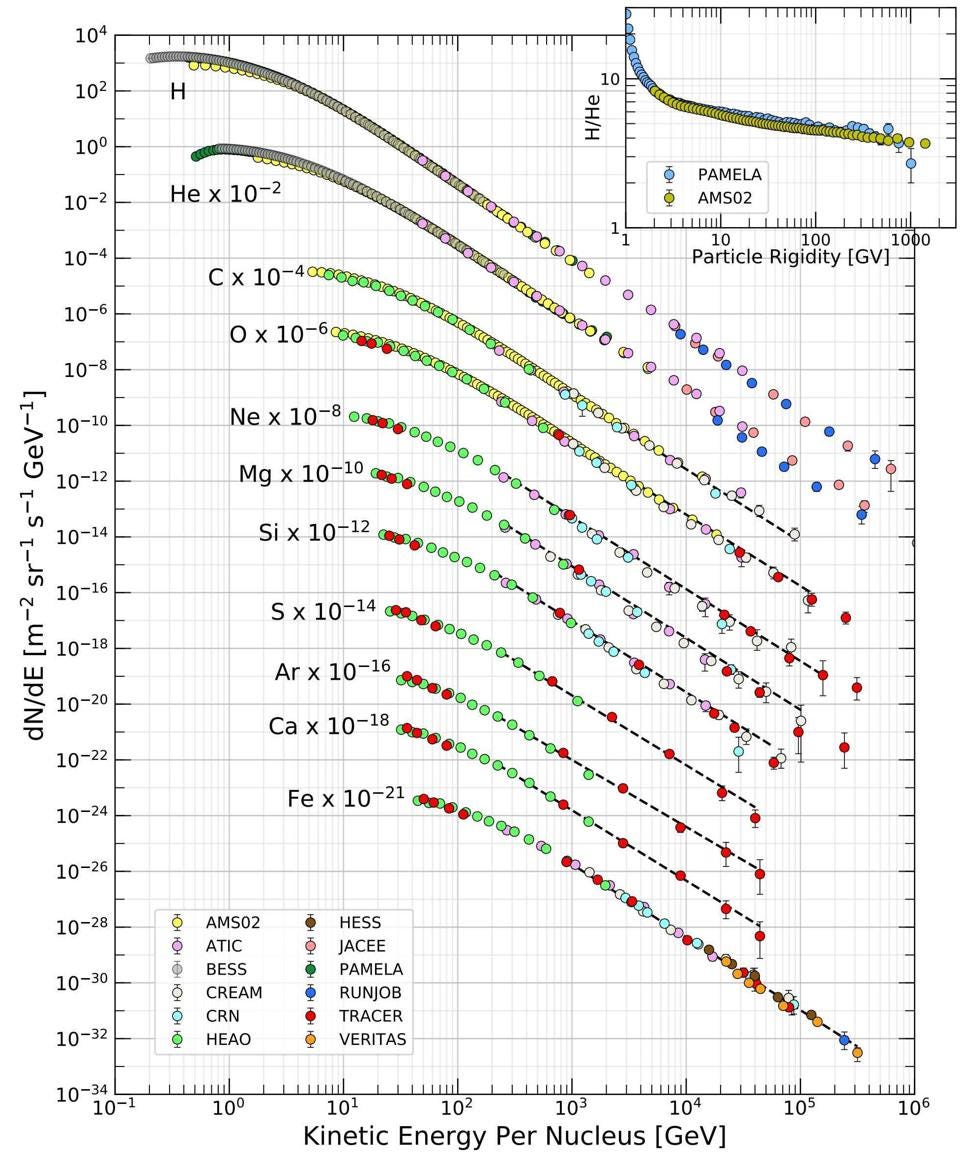
Before you start thinking of fanciful explanations like “Einstein’s relativity is wrong,” it’s worth remembering something important. Most cosmic rays are protons. However, a small but significant fraction of them are heavier atomic nuclei: helium, carbon, oxygen, neon, magnesium, silicon, sulphur, argon, calcium, all the way up to iron. But whereas hydrogen is the most common nucleus as a single proton, iron typically has a mass that’s 56 times as heavy, with 26 protons and 30 neutrons. If we consider that the most energetic particles might be made out of these heaviest atomic nuclei rather than mere protons, the paradox vanishes and the GZK “speed limit” remains intact.

Although it was quite a surprise when the first particle exceeding the GZK limit was discovered back in 1991 — so surprising that we named it the Oh-My-God particle — we now understand why that’s possible. There isn’t an energy limit for cosmic rays, but a speed limit: one that’s approximately 99.99999999999999999998% the speed of light. Whether your particle is made only of a single proton or many protons and neutrons bound together isn’t important. What’s important is that, above that critical speed, collisions with photons left over from the Big Bang will create neutral pions, which cause you to lose energy rapidly. After only a handful of collisions, you’ll be compelled to drop below that critical speed, consistent with both observation and theory.

These graphs show the spectrum of cosmic rays as a function of energy from the Pierre Auger Observatory. You can clearly see that the function is more-or-less smooth until an energy of ~5 x 10^19 eV, corresponding to the GZK cutoff. Above that, particles still exist, but are less abundant, likely due to their nature as heavier atomic nuclei. (Credit: Pierre Auger Collaboration, Phys. Rev. Lett., 2020)

It’s true that no massive particles can ever reach or exceed the speed of light, but that’s just in theory. In practice, you have to move about ~60 femtometers-per-second slower than the speed of light, or collisions with the leftover photons from the Big Bang will spontaneously produce massive particles — neutral pions — that rapidly cause you to shed energy until you’re traveling below that slightly more restrictive speed limit. Additionally, the most energetic ones aren’t faster than they should be. They’re just more massive, with their kinetic energy spread out over scores of particles instead of a single proton. Overall, particles not only can’t reach the speed of light, but can’t even maintain their speed if they’re too close to it. The Universe, and specifically the leftover light from the Big Bang, ensures that it’s so.