Can we see farther back in space than we can in time?

- When we look back at objects in space, we're not seeing them as they are now, but as they were a long time ago.
- For nearby objects, our distance from them in light-years equals the "lookback time" in years.
- But for extremely distant objects, we can see back more than three times as far, in terms of light-years, than we can in terms of years, and that's because of our expanding universe.
No matter where you look in the universe, in any direction, your line of sight will eventually run into some type of matter or radiation. The Earth is embedded in the solar system, with planets, moons, rocky and icy bodies, dust, and plasma particles permeating our environment. Beyond our own backyard are stars, gas, and dust strewn throughout the Milky Way, and at even greater cosmic distances are galaxies, quasars, and the matter in the intergalactic medium. If you somehow manage to pick a line of sight that doesn’t run into any of those, you’ll still encounter something: the cosmic microwave background, which is thought to be the leftover radiation from the early stages of the hot Big Bang.
And yet, no matter what we observe in any direction, two properties will correspond to whatever object we see:
- We are seeing the object not as it is today, but as it was a finite amount of time ago: when it emitted the light that’s now striking our eyes.
- That object is currently a specific distance away from us; if we could somehow “freeze” time and measure the distance between ourselves and that object, we’d get a certain value.
You might think that these two properties — time and distance — would be equal. A star whose light arrives after a journey of 10 years is 10 light-years away; a galaxy whose light arrives after a 100-million-year journey is 100 million light-years away; light from the Big Bang that arrives after a 13.8-billion-year journey has the emitting location 13.8 billion light-years away.
But that isn’t true at all — and the expanding universe is to blame.

One of the laws of physics that gets drilled into us is this: there’s a speed limit to the universe, called the speed of light, and absolutely nothing can travel faster than that. If you’re a completely massless entity, like a photon or a gluon, you absolutely must move at the speed of light, as no other speed is possible. If you have a positive, non-zero mass, however, you can only approach, but never reach, the speed of light; you must always travel slower than it.
Therefore, it stands to reason, if something emits light at any point, that light can only travel directly away from the source that emitted it. After one second, the light will be 299,792.458 kilometers away from the source: one light-second. After one year, the light will be 9.46 trillion kilometers away from the source: one light-year. And after one billion years, the light will be one billion light-years away from the location where it was emitted.
This type of calculation is sensible, straightforward, and intuitive. Under the laws of special relativity, it’s absolutely correct. However, our universe is not governed by special relativity, but by something more.
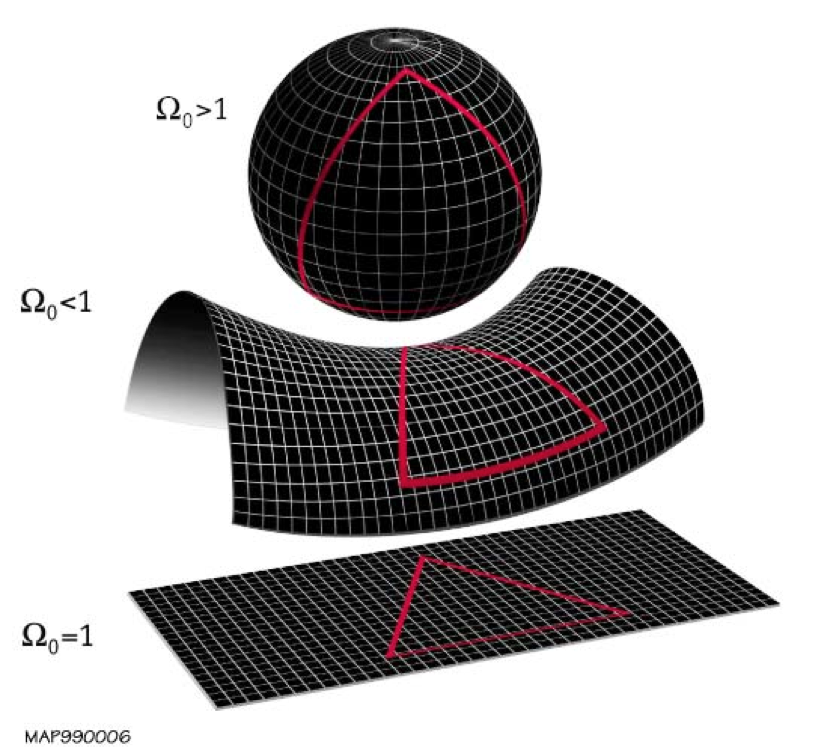
The analysis we just covered only applies if space has two specific properties that we know it does not actually possess. For starters, space would need to be flat: like a three-dimensional Euclidean grid. Flatness can be defined for any general space, and the way you can tell whether your space is flat or not is by picking three points and connecting them by drawing three lines to make a triangle. You then add up the three interior angles of the triangle that you just drew and compare the result to what you would get if you simply drew a triangle on a flat piece of paper: 180°.
However, not all pieces of paper are “flat” where the angles add up to 180°, and not every instance of space is, either. If you drew a triangle on a globe, you’d find that the interior angles always summed up to more than 180°, with larger triangles resulting in greater departures from 180°. Similarly, if you drew a triangle on a horse saddle, you’d find that the interior angles always summed up to less than 180°. The universe is not like a piece of paper. Because of the presence of matter and energy, the fabric of space gets curved depending on how matter and energy — and especially mass — is distributed.

But even more importantly than being curved, the fabric of space is not static. This is more than just the intuitive, “Okay, masses move around, and masses determine how space is curved, so therefore the spatial curvature changes.”
That statement is true, but there is something much more profound happening. Under the laws of Einstein’s general relativity, which is our theory of gravity, a universe filled with matter and energy cannot be static and stable. If you start a universe in a static state and simply allow it to gravitate over time, it will not remain static. Instead, it will collapse, and in short order, your entire universe will come to an end, forming an inevitable black hole.
This clearly hasn’t happened to our universe and there’s an excellent reason why. If you uniformly fill your universe with matter and energy, it must either expand or contract; the distance between any two well-separated points will change over time. We have no way of knowing, from first principles, which one of these would wind up describing our universe, the same way you cannot know whether the square root of 4 is +2 or -2. Both expansion and contraction are mathematically allowable solutions for our universe, but we have to measure the universe itself to find out which one is occurring.
The key observations for solving this problem were made all the way back in the 1910s and 1920s. In fact, it was a combination of three sets of observations that led to a solution for this puzzle.
- Henrietta Leavitt’s work on Cepheid variable stars, which related the time period it takes for such a star to go from maximum to minimum brightness, and back again to the intrinsic brightness of the star itself.
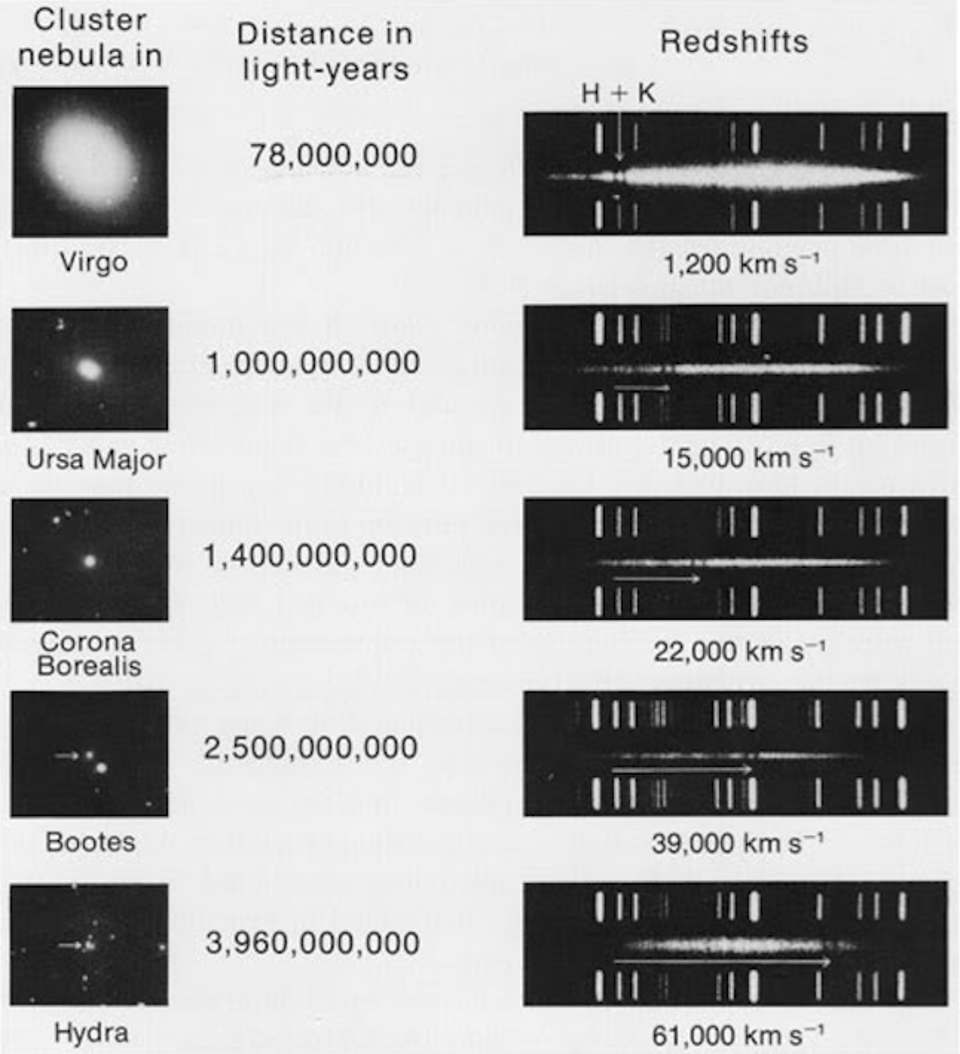
- Vesto Slipher’s work on redshift, in which he measured a significant number of the spirals and ellipticals in the sky and determined, from the shift of their emission and absorption lines, how quickly they appeared to be moving toward or away from us.
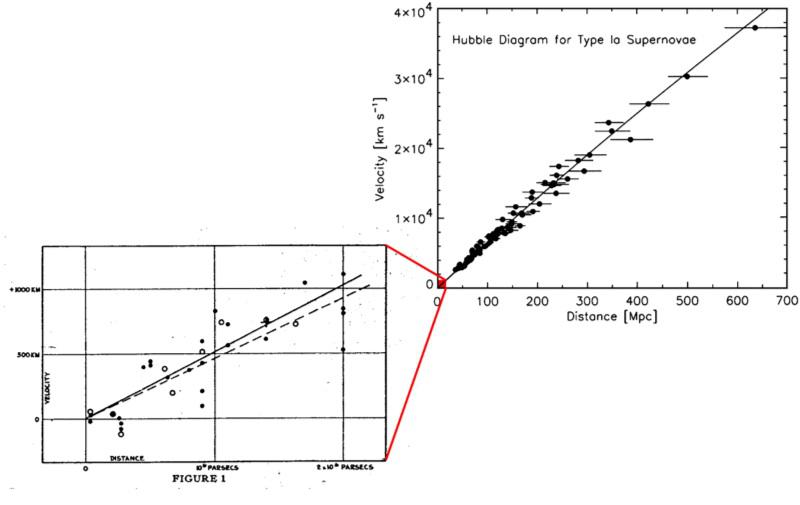
- Edwin Hubble’s work, assisted by Milton Humason, in which individual Cepheid stars were measured in those spirals and ellipticals.
With those combined properties, we could determine both the distance to a spiral or elliptical galaxy as well as the inferred motion of those galaxies. When that data was put together, both initially and in modern times, the result is unambiguous: the farther away an object is, the more its light is redshifted and the faster it appears to be receding from us. In other words, the universe must be expanding.
This has major implications for the idea of a static universe. If the universe were static, then the amount of time it took light to travel a certain distance — from the emitting source to the observer that absorbed it — would be exactly equal to the conversion from years to light-years. Because light must travel at the speed of light, the light arriving at our eyes today from:
- an object one light-year away took a year to journey to us
- an object one million light-years away took one million years to journey to us
- an object ten billion light-years away took ten billion years to journey to us
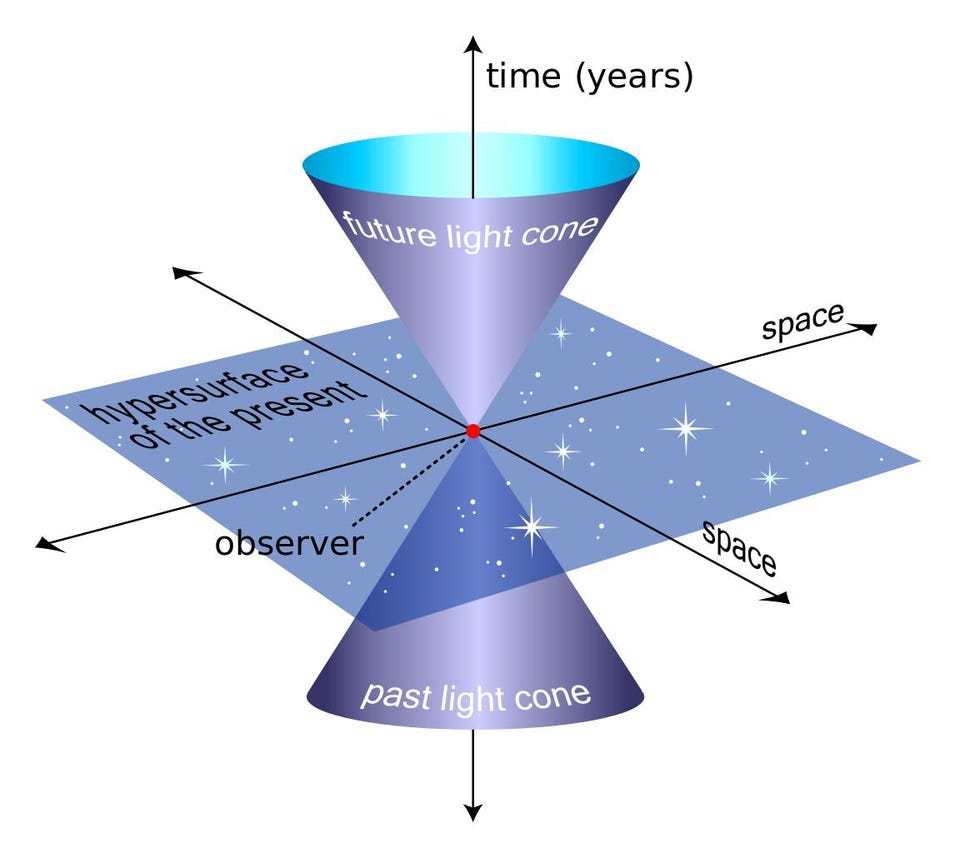
And so on. This means that, if our universe is only 13.8 billion years old, which is the amount of time elapsed since the Big Bang, then the most distant light we could possibly see must be arriving to us after a journey of 13.8 billion years, and hence that light must have traveled 13.8 billion light-years. This is consistent with the spacetime tool known as a light cone, where everything inside the cone is connected to us, meaning a signal from it could affect us (or a signal from us could affect it), but everything outside the cone is disconnected, meaning no signals can be exchanged.
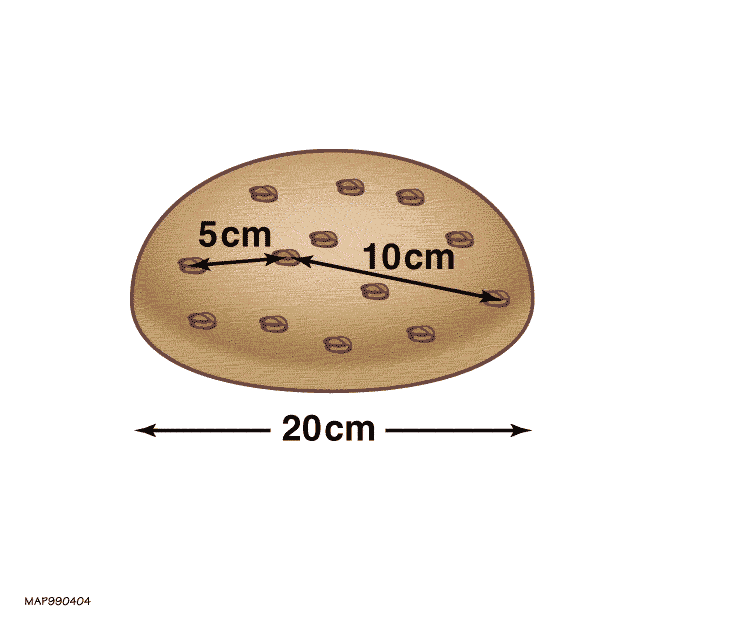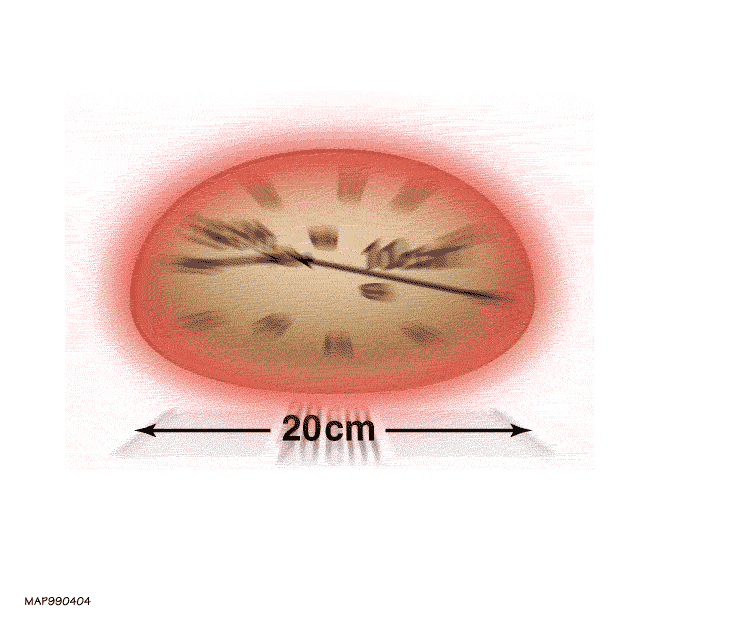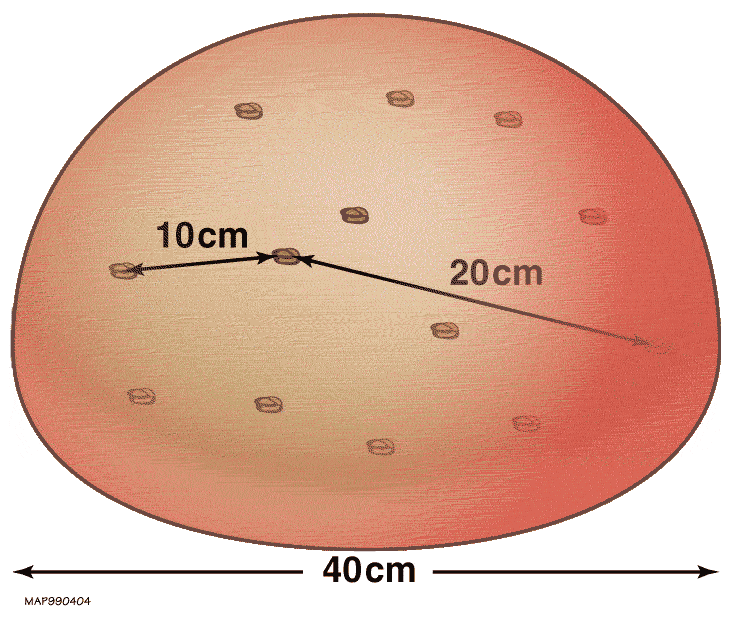
But the scenario we live in — an expanding universe — changes everything. Instead of viewing space like a grid with objects strewn about it, we should be viewing it as a ball of leavening dough with raisins embedded in it. As time evolves, the fabric of space expands, just as the ball of dough rises. The raisins themselves, however, do not expand with the universe, but they do get farther apart from one another.
In fact, if you imagine yourself as any one raisin, you’ll notice that the nearby raisins appear to expand slowly away from you, because there’s only a small amount of leavening dough between your raisin and the other nearby raisins. However, the more distance there is between your raisin and another, the more dough there is between you as well, which translates into more leavening and a greater increase to your relative distance over the same amount of time.
Each raisin represents a gravitationally bound object in our universe, like our Local Group of galaxies. The Virgo Cluster is a raisin; the Leo Group is a raisin; the Coma Cluster is a raisin, etc. Because they are bound by gravity, they themselves don’t expand, but each individual structure that’s not bound to another expands away from every other such structure — just like raisins in this rising ball of dough.
This means that, within our own galaxy or our own Local Group, the expansion of the universe is completely negligible. It is only on large cosmic scales — where we observe objects that might be bound to one another in a larger structure, but not bound to the same structure we are part of — that the expansion of the universe rears its head. The effects of “masses in motion” and how they change the curvature of spacetime are always at play, but these effects are typically small: on the order of one part in 1,000 when it comes to changes in distance.
When we are talking about cosmic distances to other objects within our Local Group, an object’s distance from us in light-years and the number of years it took for the light to travel from that object to our eyes are equivalent. Astronomers call this the “lookback time.” Dividing the object’s distance by the speed of light will give us the lookback time to ~99.9% precision, so long as the expansion of the universe is negligible.
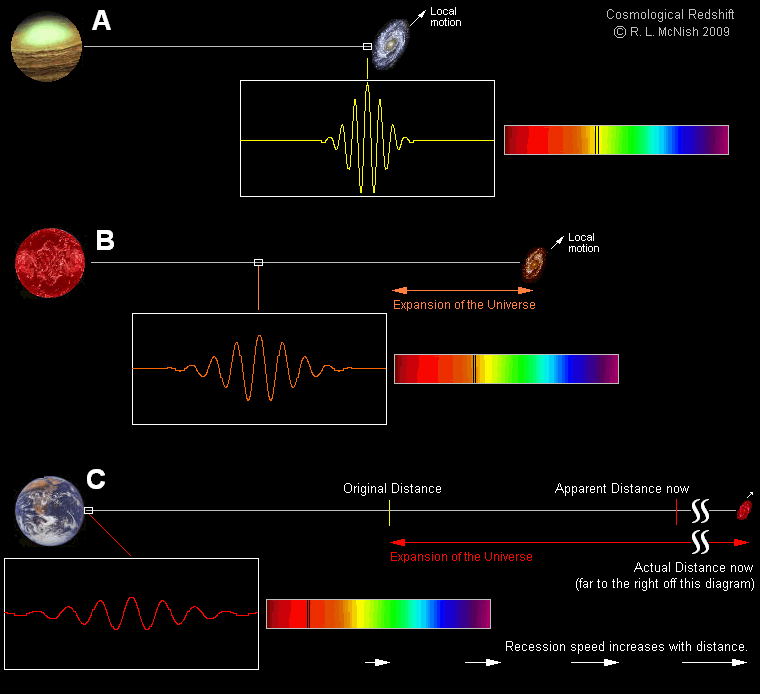
But on larger cosmic scales, something far more intricate is going on. When light comes to us from a more distant object, like a galaxy or quasar from outside the Local Group, the following process occurs:
- Light gets emitted from the distant object at the speed of light.
- As the light travels toward its destination through intergalactic space, however, the distance between the emitting object and the object that will eventually absorb it continues to increase.
- While the light continues its journey, the expanding universe stretches the wavelength of the light, causing it to lengthen, which we observe as a redshift.
- Simultaneously, the distance between the emitting object and the eventual absorber also continues to increase.
As a result, when the light finally arrives, the original distance between the emitter and the absorber was much smaller than the distance is now. Meanwhile, if you were to multiply the lookback time by the speed of light, you would get an in-between distance: larger than the original distance but smaller than the distance today. That’s where the discrepancy between the age of the universe, as measured from the start of the hot Big Bang, and the distance to the farthest objects visible, corresponding to their separation from us today, comes from.

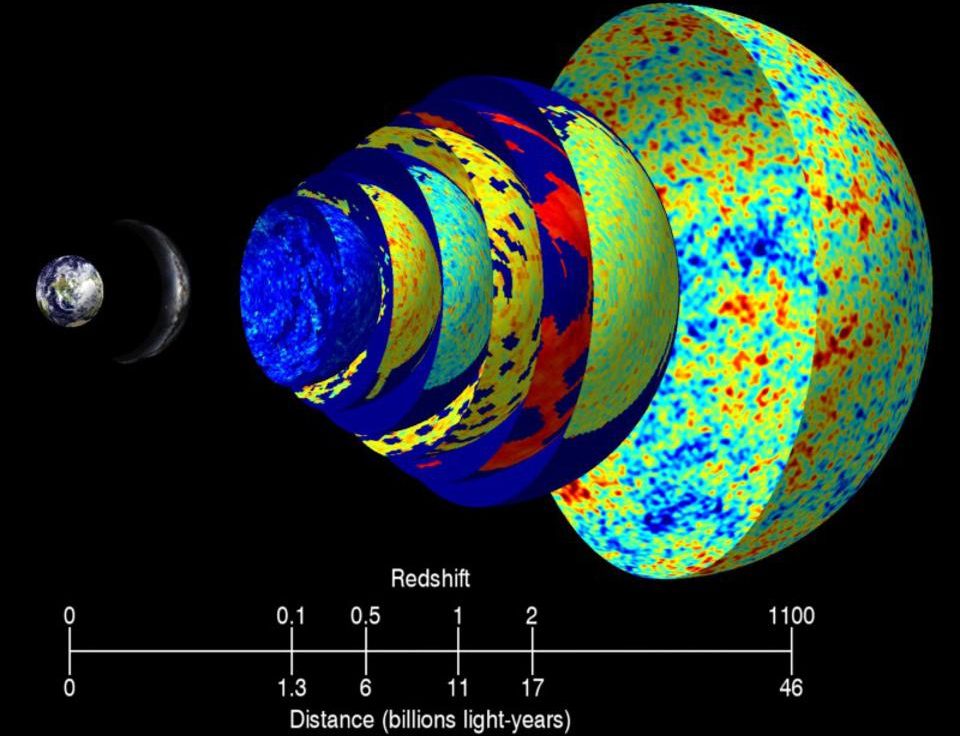
Perhaps surprisingly, this difference between lookback time and the present distance between ourselves and a distant object is only important on large cosmic scales. The most prominent galaxies in our night sky — including Andromeda, the Pinwheel galaxy, Bode’s galaxy, and the Sombrero galaxy — appear as they were the same number of “millions of years ago” as their distance from us in light-years. A galaxy whose light arrives after a 100-million-year journey is now 101 million light-years away — a minuscule difference.
But with very large distances, the expanding universe starts to play a major role:
- Light arriving from 1 billion years ago corresponds to an object presently 1.036 billion light-years away.
- Light arriving from 5 billion years ago corresponds to an object presently 6.087 billion light-years away.
- Light arriving from 10 billion years ago corresponds to an object presently 16.03 billion light-years away.
- Light arriving from 13.78 billion years ago corresponds to an object presently 41.6 billion light-years away.
It is not that we are seeing farther back in space than we are in time. Instead, it is that space and time are related, the universe is expanding, and the effects of the expansion are cumulative: they affect the light traveling through the universe during every step of its journey. The light that travels the longest gets stretched by the greatest amount, and the object that emitted that light is now at a greater distance because the universe is expanding. We can see objects up to 46.1 billion light-years away precisely because of the expanding universe.
No matter how much time passes, there will forever be limits on the objects we can observe and the objects that we can potentially reach. As long as space and time are linked by the laws of Einstein’s relativity, these limits will never be circumvented.