Why reimagining the particle accelerator is so challenging

- There are many plans for building a new, next-generation particle collider to succeed the Large Hadron Collider at CERN, as many physicists hope to answer questions that the LHC is incapable of answering.
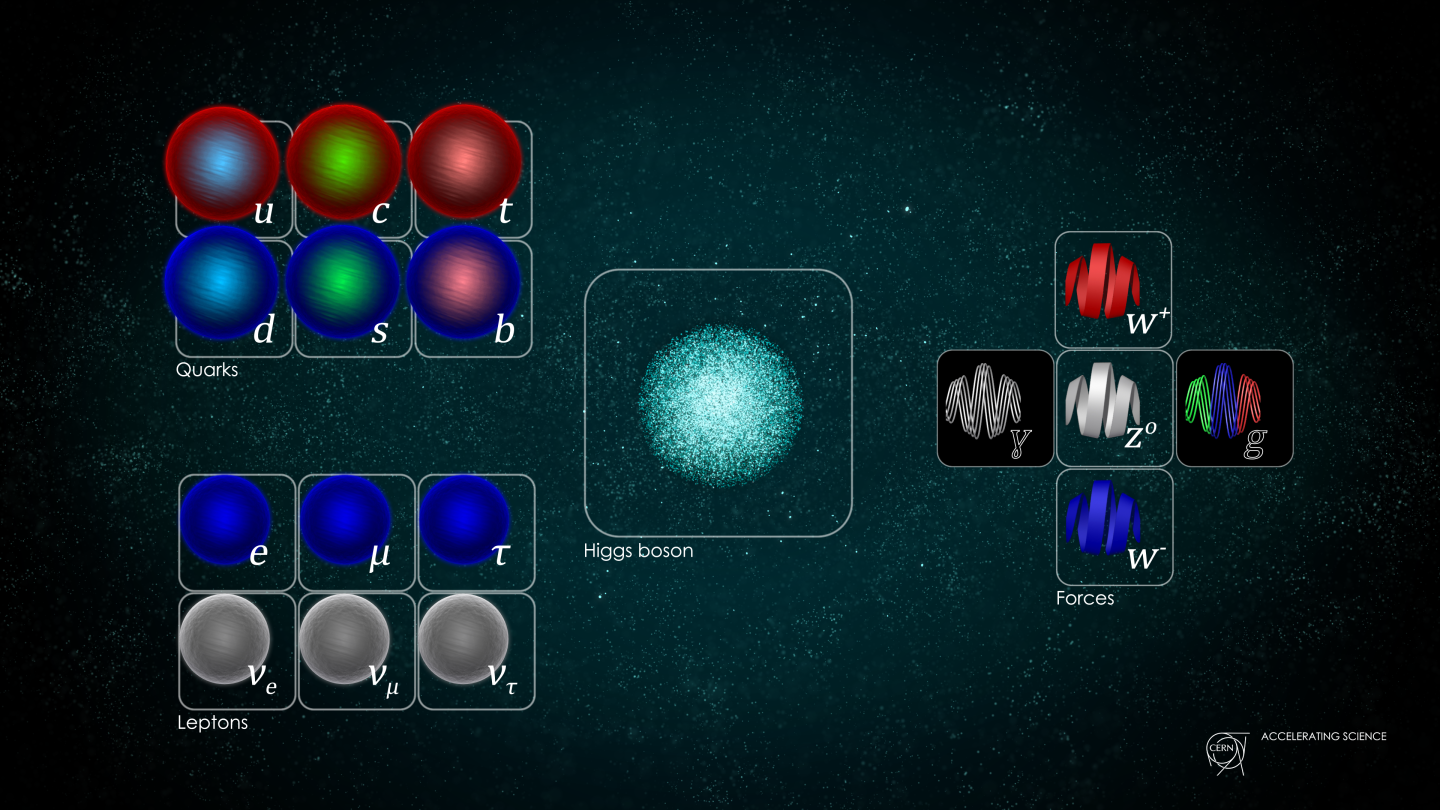
- In addition to searching for new particles, a new accelerator/collider should also serve as a factory for the heaviest Standard Model particles of all: the W, Z, top quark, and of course the Higgs, producing them in great numbers for study.
- But which of the four designs should we choose? A linear lepton collider? A circular lepton collider? A circular hadron collider? Or a novel muon collider? All four options are worth considering, but each has drawbacks, too.
Right now, over in Europe, the world’s most powerful particle accelerator in history — the Large Hadron Collider — is once again colliding particles in record fashion: at the highest energies and with the greatest collision frequencies (what accelerator physicists call luminosities) of all-time. Record numbers of collisions at record-high energies are going to translate into the production of more Higgs bosons (as well as many other interesting particles) than ever before. But even this iteration of the Large Hadron Collider, the high-luminosity version (the HL-LHC), is still going to be severely limited in terms of what types of questions it will be able to answer.
- Is this truly the Standard Model Higgs boson that we’ve discovered, or are there other particles with the same quantum numbers as the Standard Model Higgs that mix together with it?
- When a newly created Higgs boson then decays, does it purely follow the Standard Model’s predicted decay channels, or does it (at least sometimes) decay in a non-standard, unexpected way?
- When any of the heavy, exotic particles (W bosons, Z bosons, top quarks, etc.) are created and then decay, do they show any evidence for non-standard (i.e., non-Standard Model) behavior?
- And are there any new, exotic particles that can be created at a collider that fall outside of what the Standard Model predicts?
All colliders have limits to what they’ll be able to probe: even the HL-LHC. To find out more information about the fundamentals of our Universe, a new collider will be needed. But which one should we build? Here’s what everyone should know about the four major types of collider presently under consideration.
The four options
If you want to create high-mass particles — particles with the highest rest-mass energy to them, like the W-boson, Z-boson, Higgs boson, and top quark — you need enough energy available for particle creation: energy in the form of E = mc². Not just total energy, but energy available to create new particles. That means, if you want to create something like:
- a W-boson (of energy ~80 GeV),
- a Z-boson (of energy ~91 GeV),
- a Higgs boson (of energy ~125 GeV), or
- a top quark (of energy ~173 GeV),
you need to have two particles (or a particle-antiparticle pair) collide together so that when you switch to the center-of-mass (or center-of-momentum) frame of the collision, there’s at least as much “leftover” energy (initially in the form of kinetic energy of the particles before the collision) as you need to create those particles in the first place.

This means you need to accelerate two types of particles (either a lepton-antilepton, a hadron-antihadron, or a hadron-hadron) in two different directions, collide them together so that their net momentum is zero, and to build a detector around the collision point. The four main options for doing so are:
- A linear electron-positron collider, like SLAC was back in the 1970s and 1980s.
- A circular electron-positron collider, like LEP was through 2002: the predecessor to the LHC.
- A circular hadron-hadron collider, like the LHC is today.
- Or a (circular) muon-antimuon collider, which is a novel type of collider that has never been built.
For good reasons, no one is considering building a circular proton-antiproton collider like Fermilab’s Tevatron was until it was decommissioned in 2011: the tiny amount of extra energy you get from quark-antiquark collisions versus quark-quark collisions is negligible at high energies, as most of the colliding particles are actually gluon-gluon collision at those energies, whereas you can increase your collision rates (and luminosities) by factors of many thousands (or more) by using protons instead of antiprotons.
Let’s look at the pros and cons of each of these four options next.
A linear (electron-positron) collider
So, you want to create a bunch of heavy particles: W-bosons, Z-bosons, Higgs bosons, and perhaps even top quarks? The lowest-energy way to get there is to accelerate and collide leptons, like electrons and positrons, at equal-and-opposite speeds onto a collision point at a very specific energy. In particular, if the energy is:
- 91.2 GeV, you will produce extraordinarily large numbers of Z-bosons,
- 160.8 GeV, you’ll produce large numbers of W+ and W- bosons, in pairs,
- 216.3 GeV, you’ll produce large numbers of Higgs bosons (as this is the rest energy of a Z-boson plus a Higgs boson),
- 346 GeV, you’ll produce large numbers of top quarks, as this is the energy for making a top-antitop pair.
These hard-to-create particles, which live for only a tiny fraction of a second (around ~10-24 seconds apiece or even less), are normally produced at hadron colliders at several TeV of energy. With an electron-positron collider, they can be produced at much lower energies (below 0.35 TeV), in very clean collisions (without all the extra junk that’s inside of hadrons, like protons), in a very controllable fashion. Simply by tuning how much energy goes into each electron and positron that will collide at the desired collision point, you can maximize the type of process and particle you want to study.
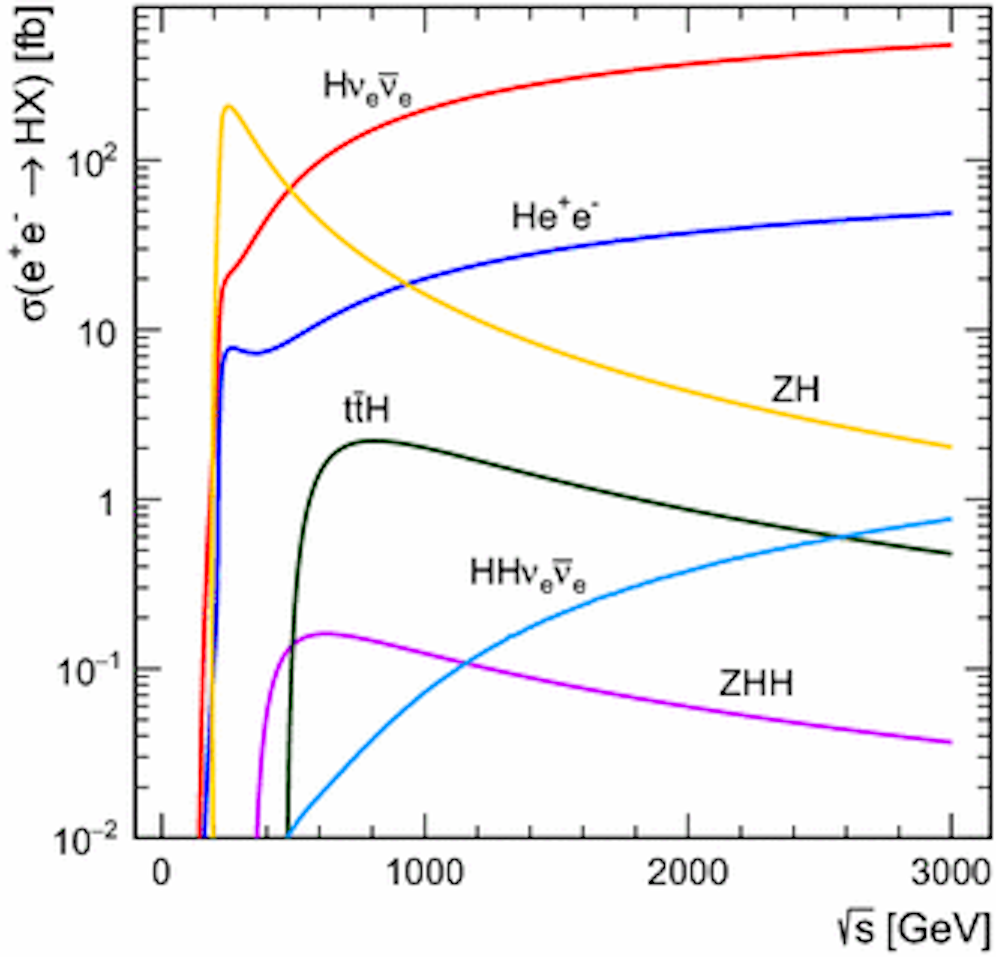
This allows us to quantify the Higgs boson production from so-called Higgsstrahlung processes (creating both a Z-boson and a Higgs) versus from WW-fusion (where electron-positron collisions produce either a Higgs boson and neutrino-antineutrino pairs or a Higgs boson and a charged lepton-antilepton pair), and to produce enormous numbers of Z’s, W’s, Higgs’s, and top particles basically at will.
But there’s a drawback to this approach: technologically, we can only increase a particle’s energy by a certain amount for every meter of “accelerator” that we build. At present, that energy value is relatively modest: about 30 MeV per meter.
That means, if we wanted to build a linear collider that gets up to 346 GeV in energy at the center-of-mass of a collision point, we need a little bit more than an 11 kilometer (!) long accelerator. For comparison, this is nearly three times the length of each of the laser-arms of the LIGO detectors, and would require building an accelerator in-ground and/or above ground to compensate for the curvature of the Earth. If we can develop better technology that increases the amount of energy gain per meter, to perhaps 100 MeV per meter or more, this approach will become very attractive and the design can be much more compact. Without such an advance, however, this approach is likely to remain in the design phase.

A circular (electron-positron) collider
If we’re talking about “new construction” and a “standalone collider,” with no potential for upgrades, then a circular electron-positron collider is inferior to a linear electron-positron collider in every way. The reasons are numerous, but very straightforward to understand. Whereas a linear collider only needs accelerating magnets (to push the electron or positron “forward” and increase its energy) and focusing magnets (to keep the beam aligned and to push particles together near the collision point), a circular collider also needs bending magnets, and to keep the particles circulating without hitting the beam walls. The smaller the radius of your circle, the stronger your bending magnets need to be.
For electrons and positrons, this is a nightmare for a reason largely unfamiliar to non-accelerator physicists: there’s such a thing as synchrotron radiation. When you need a charged particle to move in a circular path, you have to bend it using either an electric field or a magnetic field, and either one of them will spontaneously lead to the emission of electromagnetic radiation: synchrotron radiation. This radiation carries energy away from the accelerated particle and prevents you from getting above a certain critical energy: an energy determined by the size of your ring. With stronger magnetic fields, more and more energy gets lost.
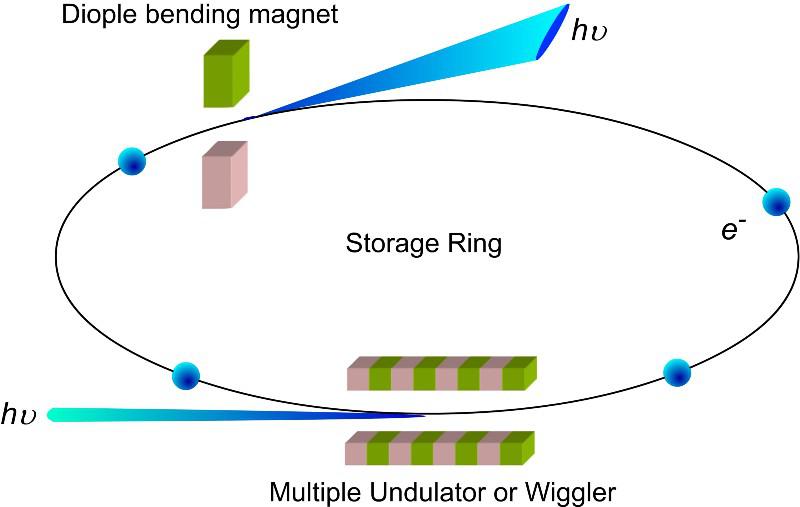
The previous most powerful electron-positron collider ever built, LEP (or LEP2, more accurately) used the same tunnel that the LHC now occupies — 27 kilometers in circumference — pushed up against the limits of this synchrotron radiation to create a maximum center-of-mass collision energy of just over 200 GeV, but not enough to reach 216 GeV: where you can create a Z-boson and a Higgs boson together. (With just a little bit more energy, they could’ve gotten there!) Although there is a push by some in the field to build “LEP3,” or to remove the LHC, to restore LEP, and to increase the magnet strength to reach that critical energy value, the cost would be great and the (low luminosity) science case is very limiting.
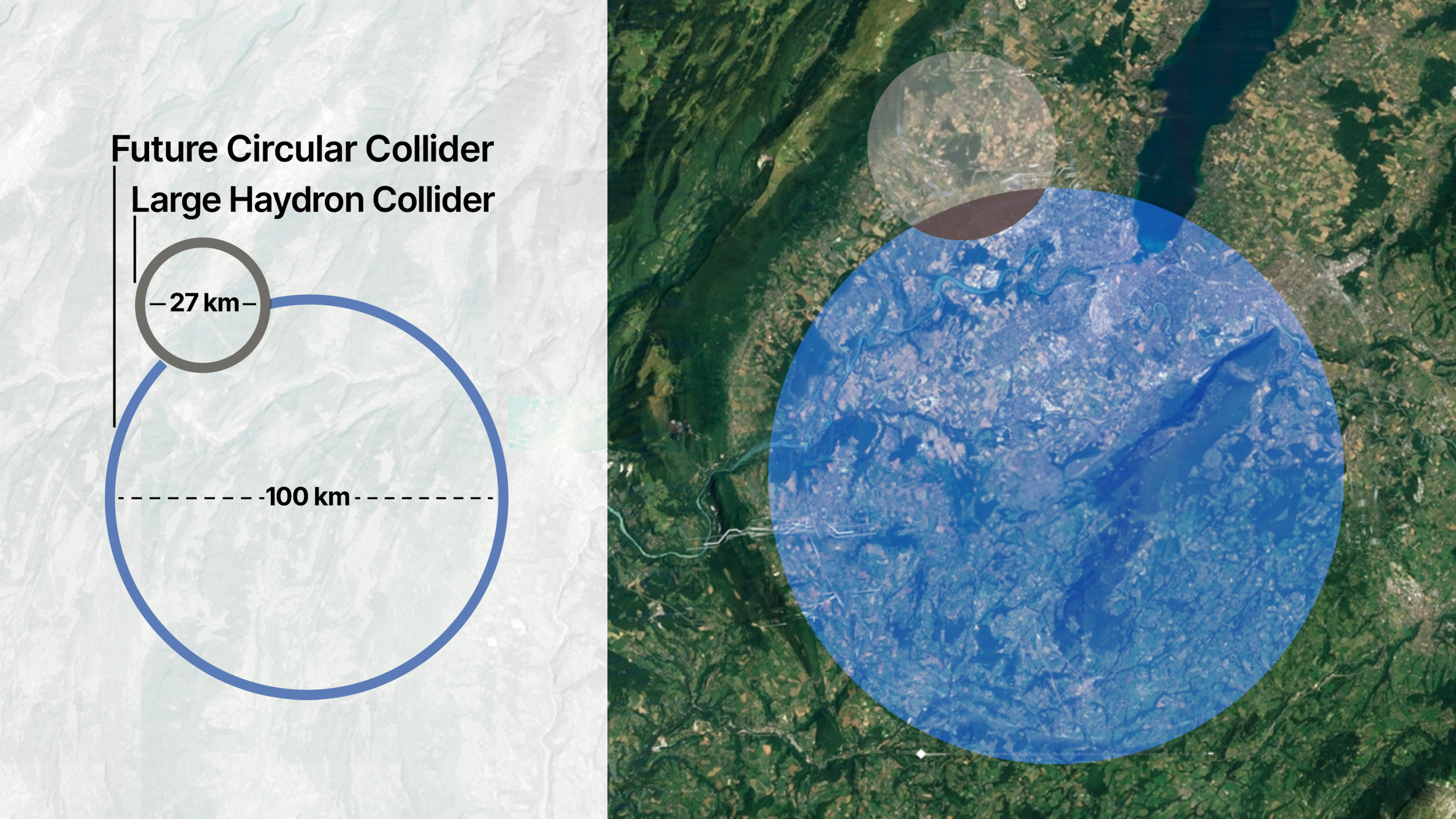
Only if we build a new, larger ring does the science case for an electron-positron circular collider become compelling, and if we do that, we have to freely admit that this will be much more costly than a linear collider of the same energy. The only reason to choose this option is if we are certain that, long-term, we will also want to insert a proton-proton (or some other hadron-hadron) collider in that same tunnel we are building now. Just as LEP and LHC both used the same tunnel (giving two machines for the price of one tunnel), a circular electron-positron collider would likely be superseded by a circular proton-proton collider. This is the plan of, for example, the Future Circular Collider (FCC) concept at CERN, but the hadron-hadron version is only going to be useful if the electron-positron version indicates that there’s something new, beyond the Standard Model, that’s worth investigating at those energies and luminosities.
A circular hadron collider
This is kind of the “ultimate” in high risk-high reward big science. There’s a very simple formula for calculating how much energy you can get out of your circular collider:
- you take the radius, R, of your ring (in kilometers),
- you multiply it by the strength of your bending magnets, B, that keep your particles in the ring (in Teslas),
- and then multiply by a constant (a number right around ½, or perhaps just slightly below it),
and that’s the maximum energy (per proton) of your hadron-hadron collider. Fermilab’s Tevatron has about a 1 km radius and about 4 T magnets in it; CERN’s LHC has about a 4.3 km radius and about 7.5 T magnets. Typically, next-generation colliders hope for about an order of magnitude improvement, or a factor of 7-to-10 in energy, over the previous generation of colliders. That would mean, for a next-generation hadron-hadron collider, we’d be looking at a ring with at least a ~13-16 km radius (80-100 km in circumference) and electromagnets that are at least ~16 T, or double the strength of the LHC’s current generation of electromagnets.
Of course, if the costs of digging a tunnel and/or building high-field electromagnets decreases, or if magnet technology improves such that producing very high-field magnets (of 40-100 T) becomes possible, the cost-benefit analysis might tip in this direction, after all. But this option, at present, is both the most expensive and, importantly, comes with no guarantee of finding anything novel.
A muon collider
On paper, this looks like the most brilliant option of all, as new generations of physicists get (understandably) excited about this possibility every 10-15 years or so. Muons (and antimuons) are also leptons, like electrons (and positrons), but 206 times heavier. As a result, they:
- accelerate and gain energy like electrons,
- emit much less synchrotron radiation in a circular collider than electrons (and positrons) do, by a factor that scales as ~(1/206)4,
- collide in clean, perfectly annihilating collisions with their antiparticle (like electron-positron collisions),
- and allow 100% of their energy to be available for particle creation, via Einstein’s E = mc².
Using the same tunnel that a circular electron-positron collider would use, you could achieve energies that were hundreds of times as great using muons and antimuons instead.
There is a big drawback, unfortunately, that simply can’t be ignored: even though it’s fairly easy to create muons, the sad reality is that muons are unstable, and decay relatively quickly. With a mean lifetime of just 2.2 microseconds, even special relativity — accelerating these muons (and antimuons) close to the speed of light and extending their life through relativistic time dilation — can’t prevent the overwhelming majority of muons from uselessly, and damagingly, decaying away.
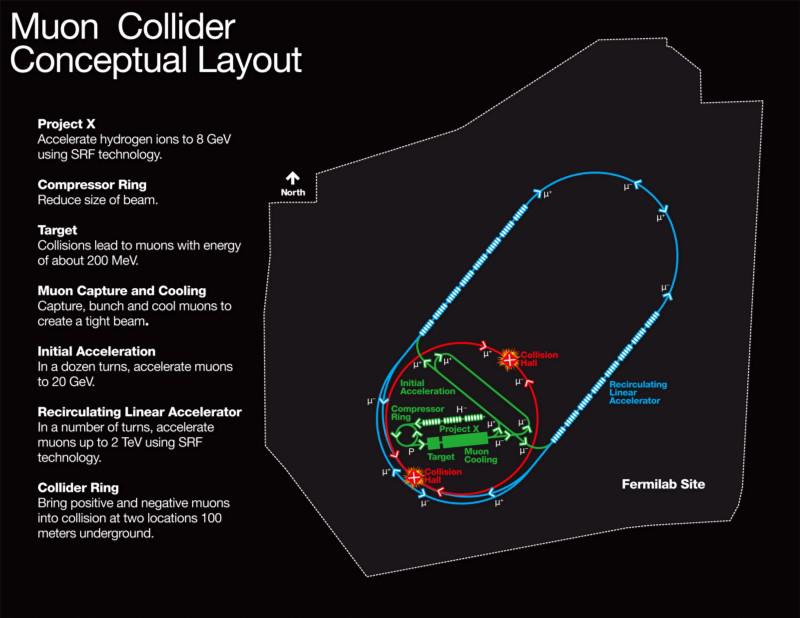
Making muons is easy: you collide a beam of low-energy protons into a fixed target (like a piece of acrylic), the overwhelming majority of the particles that come out in a “shower” will be charged pions, and those charged pions will then swiftly decay into muons (for the negative pions) and antimuons (for the positive pions), but then the clock starts ticking. You have only a few microseconds in the muon’s (or antimuon’s) rest frame to:
- collimate them,
- accelerate them,
- circulate them,
- and collide them with their antiparticle counterparts at the critical collision point.
Miss your window, and your muon (or antimuon) will decay into an electron (or positron), and that decay product will smash into your accelerator’s wall, where damage will cumulatively add up over time.
Which type of collider, then, should we build next? The answer absolutely isn’t “none of them,” as there is an enormous science case in favor of probing the physics of heavy, short-lived particles in the search for new phenomena. But which path turns out to be the smartest, and most cost-effective, is entirely dependent on which technological avenue advances the fastest. If it’s energy-gain-per-meter, we should build a linear electron-positron collider. If it’s in muon survival technology, a muon collider would be revolutionary. And if it’s in tunnel building and/or bending magnet technology, a next-generation circular collider could outclass them all.
All of these paths face challenges — politically, economically, and technologically — but they all point the way forward for directly exploring the frontiers of fundamental physics. At present, the smartest move might be to technologically research all of these options, and for the field to go all-in on the most promising one.