Ask Ethan: How can “the Hubble constant” be a constant?

In all of physics, some of the most important properties inherent to the Universe itself are constants of nature. The speed of light in a vacuum, the strength of the gravitational force between two masses, and the constant inherent to the quantum nature of the Universe, Planck’s constant, are all examples of fundamental parameters that never change, regardless of circumstances. But it’s also plausible that some of the so-called constants aren’t exactly constant, but vary either across space or time, changing as the Universe and its properties also evolve.

Could that be the case for the so-called Hubble constant? In fact, does the idea that the expansion of the Universe could be constant even make sense in light of what we know today? That’s what Warren Chu wants to know, asking:

“If Perlmutter and [Riess], in 1998, discovered that the expansion is accelerating, how can [the Hubble constant] be a constant, when it is slower for more distant sources and faster for closer sources?”

If you’ve ever heard the phrase, “The expansion of the Universe is accelerating,” which it is, alongside the idea of a “Hubble constant,” you might have wondered precisely the same thing. After all, acceleration means that some rate is increasing over time, and if the Hubble constant is the rate that the Universe is expanding, it can’t possibly be constant. Or can it? Let’s dive into the science to find out!

A visual history of the expanding Universe includes the hot, dense state known as the Big Bang and the growth and formation of structure subsequently. The full suite of data, including the observations of the light elements and the cosmic microwave background, leaves only the Big Bang as a valid explanation for all we see. As the Universe expands, it also cools, enabling ions, neutral atoms, and eventually molecules, gas clouds, stars, and finally galaxies to form.

To start, we should ask ourselves what it even means that the Universe is expanding. Most people, when they think about expansion, think about it the same way you’d think about an explosion: a series of shrapnel, moving outwards in all directions, all emanating from the same point of origin, but at different speeds. Over time, the faster-moving components will wind up farther away from the source of the explosion and will have larger recession speeds, while the slower-moving components will travel a shorter overall distance in the same amount of time, possessing smaller recession speeds.

Although that’s correct for an explosion, that’s not at all how the expanding Universe works. For one, there is no point-of-origin for cosmic expansion; the Universe appears to expand equally for all observers in all locations. For another, in an explosion, the particles that get flung outward the fastest are fewest in number, and yet in the expanding Universe, there’s a greater density of objects farther away and receding faster: the exact opposite of what an explosion would predict. And thirdly, if we traced everything that was moving away back towards a single point-of-origin, it would be remarkably close to us: less than 0.1% of the Universe’s size away from the Milky Way. Yet nowhere, not for billions of light-years in all directions, do we see anything special or remarkable about any region in space. An explosion does not explain the expansion of the Universe.

The ‘raisin bread’ model of the expanding Universe, where relative distances increase as the space (dough) expands. The farther away any two raisins are from one another, the greater the observed redshift will be by the time the light is received. The redshift-distance relation predicted by the expanding Universe is borne out in observations and has been consistent with what’s been known since the 1920s.

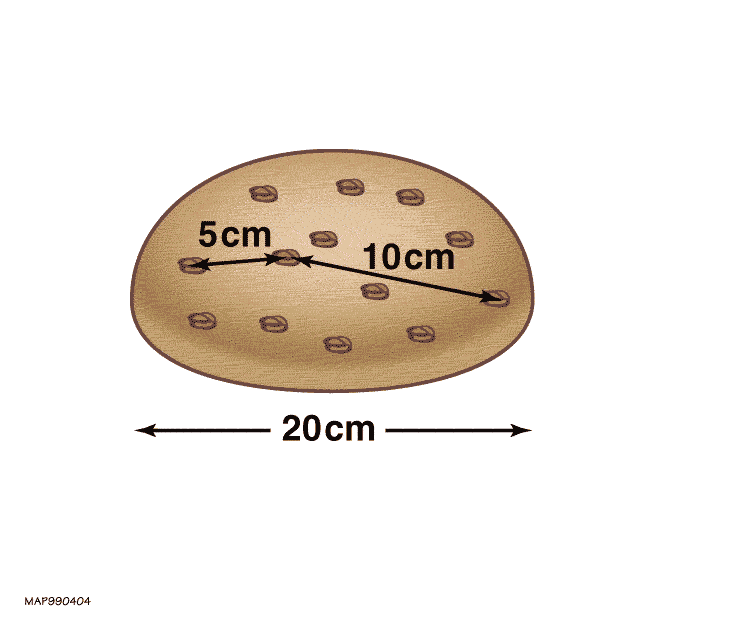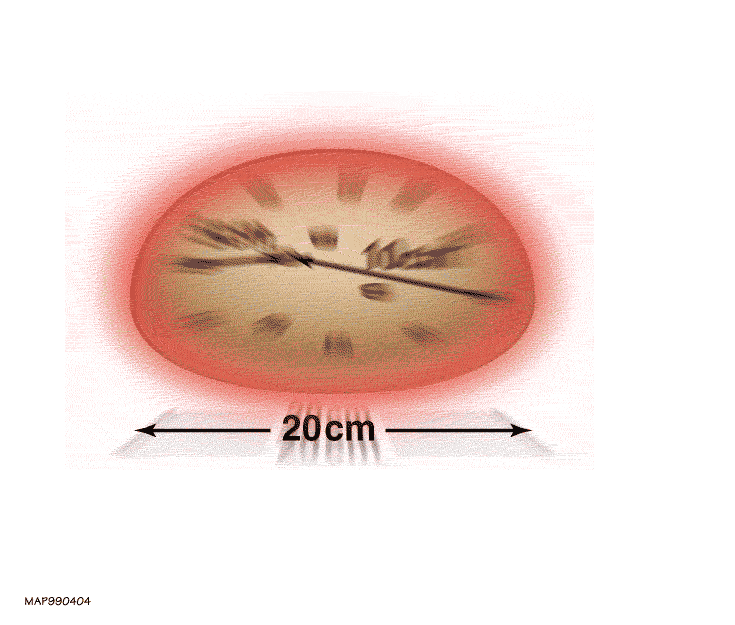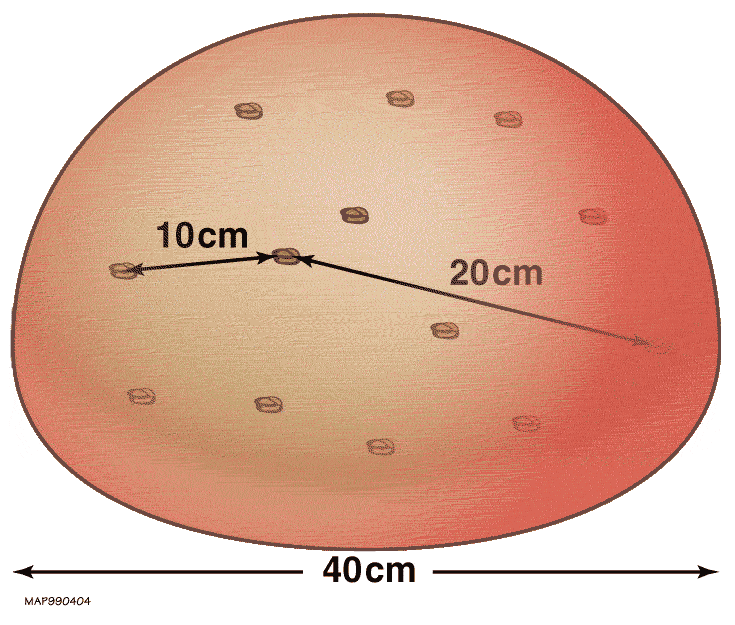
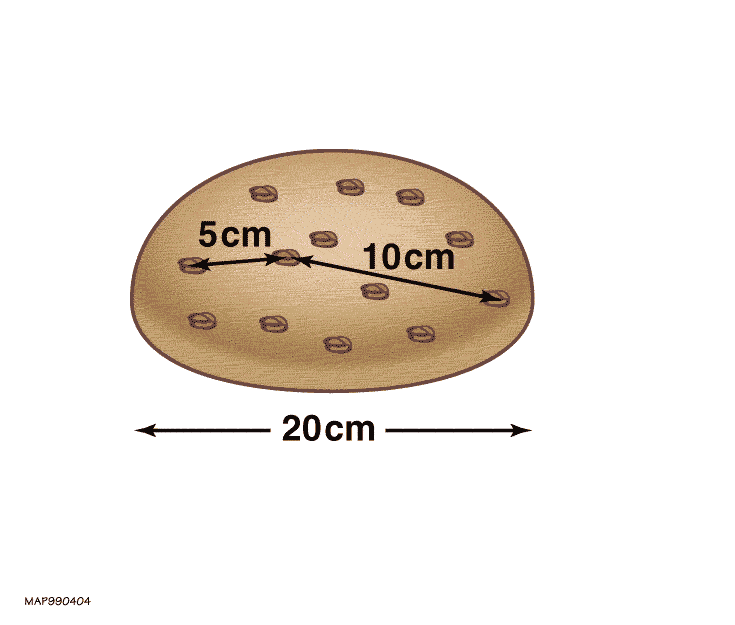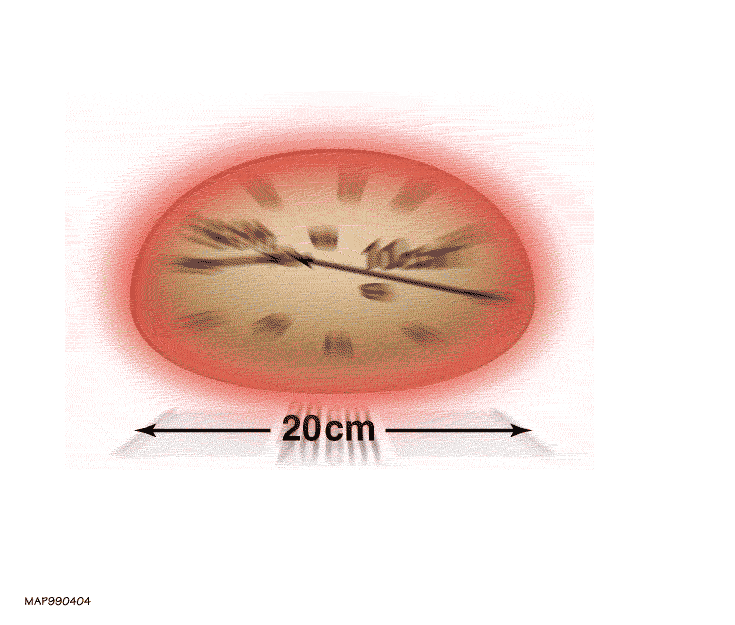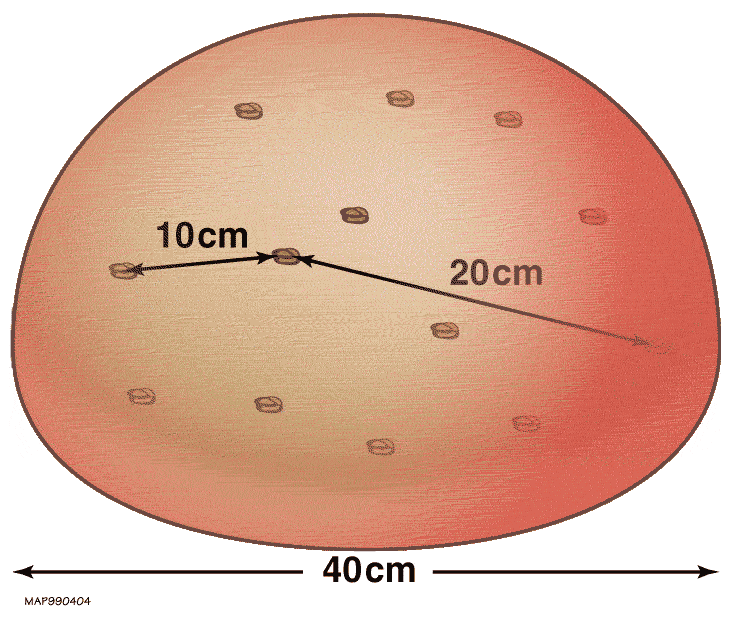
Instead, a far better analogy for the expanding Universe — and unlike an explosion, one that’s consistent with our theory of gravity, General Relativity — is that of a leavening loaf of bread. Imagine that there’s some sort of structure sprinkled randomly throughout the bread: raisins, poppyseeds, blueberries, etc., and that it starts off packed into a ball in zero-gravity. Now, imagine that you’re living within one of those objects sprinkled into the dough, that each one represents a bound structure like a galaxy or a group/cluster of galaxies, and that the dough, although it’s present, is completely invisible to you in every way.

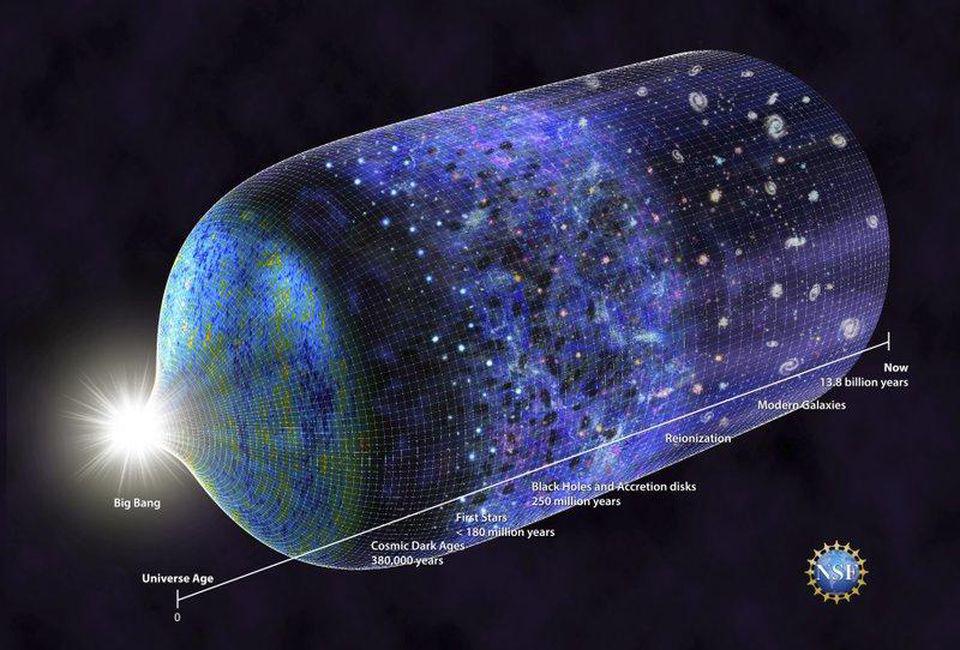
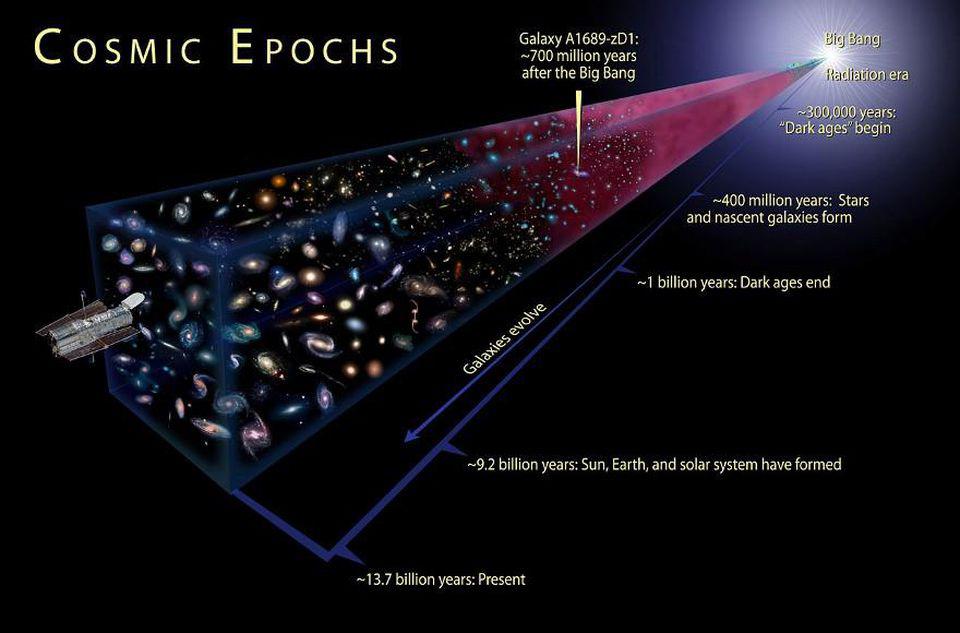
Over time, the dough will leaven, and that leavening is just like space expanding. But since the dough is invisible, what you’ll see are the other bits of structure scattered throughout the dough. The closer each raisin/poppyseed/blueberry began to yours, the slower it will appear to move away from you and the closer it will be even as time goes on. But the farther away it began, the farther away it will be and the faster it will appear to be receding. At some point, if your ball of leavening dough is large enough, a sufficiently distant object (or galaxy) will be so far away and receding so quickly that the light from it will be unable to reach you. Given that the Universe as we know it is finite in age, having begun with a hot Big Bang some 13.8 billion years ago, there are limits to both our observability and how far we can possibly reach.

The size of our visible Universe (yellow), along with the amount we can reach (magenta) if we left, today, on a journey at the speed of light. The limit of the visible Universe is 46.1 billion light-years, as that’s the limit of how far away an object that emitted light that would just be reaching us today would be after expanding away from us for 13.8 billion years. Anything that occurs, right now, within a radius of 18 billion light-years of us will eventually reach and affect us; anything beyond that point will not. Each year, another ~20 million stars cross the threshold from being reachable to being unreachable.

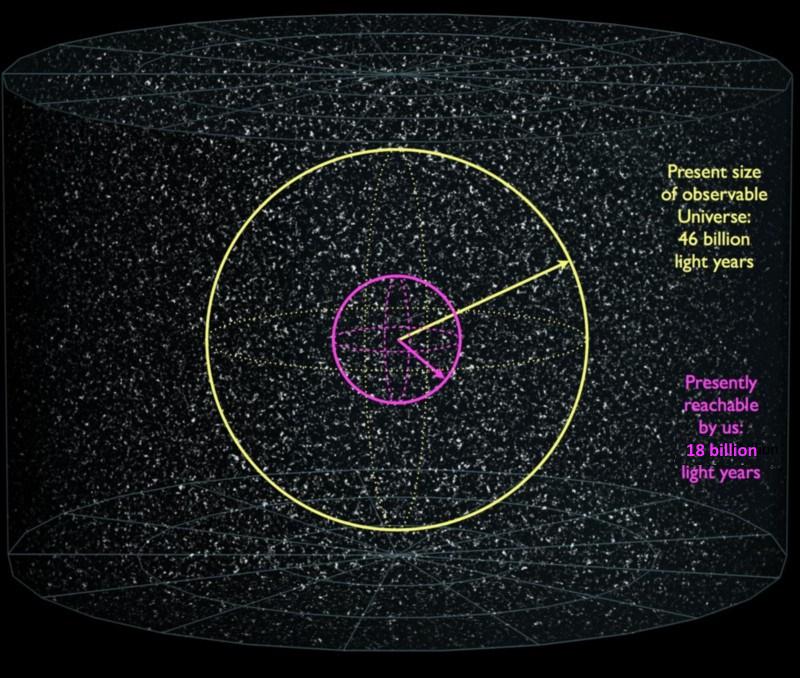
So if that’s what the expanding Universe is like, then what’s the “Hubble constant” all about?

Very simply, if we look out from our location in the Universe — and remember, in physics, location means both “here” and “now,” requiring three space and one time coordinate to fully define it — we’re going to see objects whose light is arriving at our eyes right now, at this very instant. That light will have, encoded within it, a tremendous amount of information.

1. Based on the total amount of brightness we observe that light to possess, as long as we know how intrinsically bright the object emitting it is, we can determine how far away that object is.
2. Based on the apparent size we observe that light-emitting object to possess, as long as we know how intrinsically large the object is, we can (independently of the first method!) determine how far away that object is.
3. Based on how significantly the light from that object is systematically shifted in wavelength towards longer wavelengths, we can determine — up to the uncertainty of the actual motion of the object due to the cumulative gravitational tug of everything on it — how fast that object appears to be receding from us due to the expansion of the Universe.
4. And, based on a number of measurable intrinsic properties of the object, such as the period of brightening-and-dimming-and-rebrightening of a variable star, we can (again, independently) determine the distance to that object.

When we perform these measurements, which is a task we’ve been performing for nearly a full 100 years at this point, we can plot out how far away an object is (distance) versus how fast it appears to be receding (cosmological redshift) from us.

Many different classes of objects and measurements are used to determine the relationship between distance to an object and its apparent speed of recession that we infer from its light’s relative redshift with respect to us. As you can see, from the very nearby Universe (lower left) to distant locations more than 10 billion light-years away (upper right), this very consistent redshift-distance relation continues to hold.

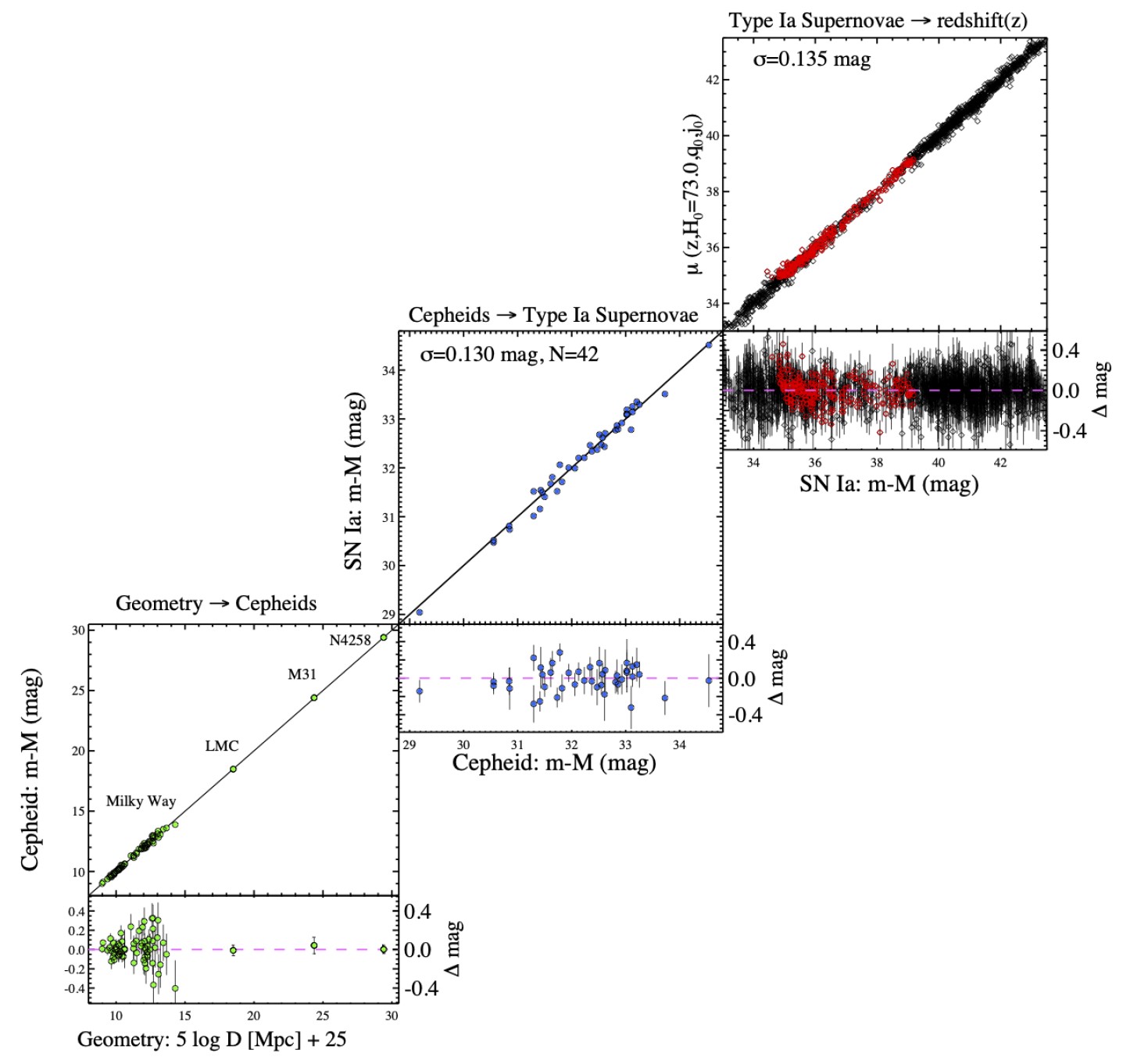
As you can see from the graph, above, pretty much every object we can measure obeys exactly the same relationship. This is the most basic, straightforward way to measure the expansion of the Universe. You plot some measure of “distance” on the x-axis and some measure of “redshift” or “inferred recession speed” on the y-axis, and you can easily see that it’s a simple relationship: the equation for a straight line.

What’s the slope of that line?

That’s what “the Hubble constant” actually is.

If the line weren’t straight, but curved either upwards, downwards, or in any other more complicated fashion, we’d have no right to call it a constant. If the line made a parabola or any shape other than a straight line, it would be a distance-dependent function. Anything other than a straight line relationship between distance and “apparent recession speed” would mean that we couldn’t describe this relationship with a constant. And yet, no matter how we make our measurements, we always get a straight line. The entire tension over the Hubble constant issue argues over what the slope of the line is, with two teams disagreeing at about the ~9% level, but both teams, including joint analyses between the teams, favor a straight line.

This graph shows the 1550 supernovae that are a part of the Pantheon+ analysis, plotted as a function of magnitude versus redshift. The supernova data, for many decades now (ever since 1998), has pointed toward a Universe that expands in a particular fashion that requires something beyond matter, radiation, and/or spatial curvature: a new form of energy that drives the expansion, known as dark energy. The supernovae all fall along the line that our standard cosmological model predicts, with even the highest-redshift, most far-flung type Ia supernovae adhering to this simple relation. Calibrating the relation without substantial error is of paramount importance.

But you were right to suspect that even though it’s a straight line, there’s a very important caveat to calling this parameter a constant: it’s only a constant to us, right now, because we’re measuring the expansion of the Universe at once single moment in time. Because of our location in the Universe — and remember, location means both “where are you in space?” (which requires 3 coordinates) and “when are you in time?” (which requires 1 coordinate) — everything that we measure is being measured right now: when the light from these distant objects reach our eyes and telescopes.

If we lived at a time that was farther into the future, we’d still measure that there was that same straight-line relationship between distance and apparent recession speed, but the slope of the line would be different: it have a smaller value than it does today.

And if we lived at a time that was farther into the past, we would have still measured a straight-line relationship between distance and apparent recession speed, but the slope of that line would have been different yet again: possessing a larger value than it does today.

Why is that the case?

A photo of Ethan Siegel at the American Astronomical Society’s hyperwall in 2017, along with the first Friedmann equation at right. The first Friedmann equation details the Hubble expansion rate squared on the left hand side, which governs the evolution of spacetime. The right side includes all the different forms of matter and energy, along with spatial curvature (in the final term), which determines how the Universe evolves in the future. This has been called the most important equation in all of cosmology and was derived by Friedmann in essentially its modern form back in 1922.

Because — and this is one of the great properties of the Universe — if you have a Universe that’s filled roughly evenly with energy, of any form or combinations of forms, in all locations and in all directions, it’s going to either expand or contract. And the rate at which it either expands or contracts is given by one simple, straightforward equation: the first Friedmann equation.

Yes, it’s not the easiest equation to solve, but it’s simple and straightforward in that every term in the equation can be understood in plain English. Here’s what each of them mean.

• On the left-hand side, there’s a term that represents the change in the scale of the Universe divided by the scale of the Universe; this is the definition of what we traditionally call the Hubble constant, which governs how the Universe either expands or contracts over time.
• On the right-hand side, the first term represents all of the matter and energy that’s in the Universe in all its various forms: normal matter, dark matter, radiation, neutrinos, etc.
• The second term on the right-hand side represents the global curvature of spacetime, and dictates whether the Universe is open, closed, or spatially flat.
• And the third and final term on the right-hand side is Einstein’s cosmological constant, which dictates the energy that cannot be extricated from space itself.

Even if you had a flat Universe (which means you can eliminate the second term on the right-hand side) and a Universe without a cosmological constant (which would mean eliminating the third term on the right-hand side, too), you’d understand immediately that the Hubble “constant” cannot be a constant in time.

While matter and radiation become less dense as the Universe expands owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant.

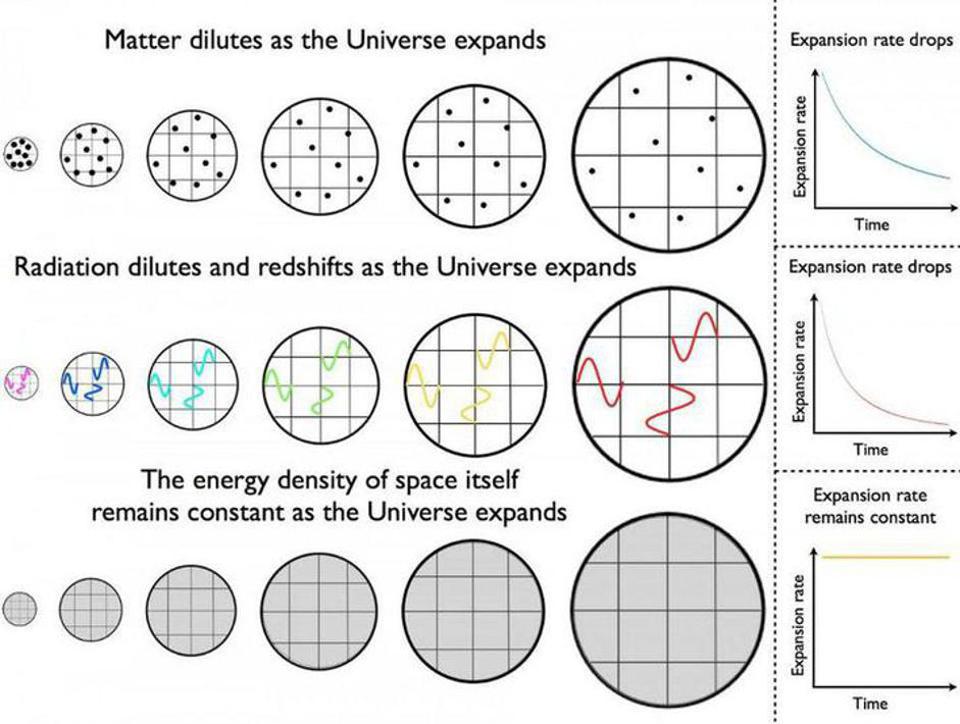
Think about it: we know some of the forms of matter and energy in the Universe. There’s normal matter, which is made of a fixed number of particles, and as the Universe expands, increasing in volume, the number of particles remains constant, and so the matter density goes down. There are photons, which move at the speed of light and have an energy that’s defined by their wavelength; as the Universe expands, the number density of photons goes down, plus their wavelength gets stretched, meaning that their energy density decreases even faster than matter’s energy density does.

And, if you like, you can fold in additional species of energy as well. You can imagine dark energy, rather than as a cosmological constant, as a form of energy inherent to space: as space expands, the energy density remains constant. You can imagine dark matter, which would behave exactly as normal matter does with respect to its effects on the Universe’s expansion. You can add in neutrinos, which behave as radiation in the early Universe (when they move close to the speed of light), and then behave as matter later on (when they’re moving slowly compared to the speed of light).

In all cases except for a cosmological constant (i.e., dark energy, to the best of our understanding), the energy density changes as the Universe expands.

Various components of and contributors to the Universe’s energy density, and when they might dominate. Note that radiation is dominant over matter for roughly the first 9,000 years, then matter dominates, and finally, a cosmological constant emerges. (The others, like cosmic strings and domain walls, do not appear to exist in appreciable amounts.) However, dark energy may not be a cosmological constant, exactly, but may still vary with time by up to ~4% or so. Future observations will constrain this further.

If the energy density changes, that means the expansion rate changes, too. The Hubble constant is only a constant everywhere in space, as we measure it right now. It’s not a constant in the sense that it changes over time.

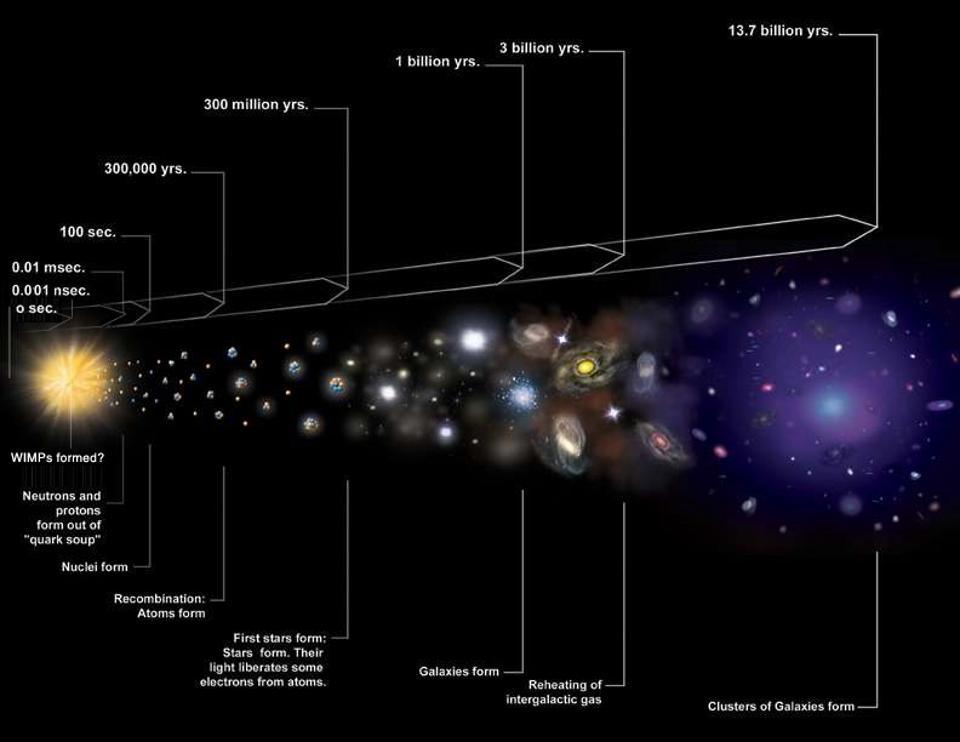
In fact, if we like, we can actually map out how we expect the size of the Universe to change over time on account of the different forms of energy that are present within it.

As the Universe grows, it gets less dense, and the density drops. Initially, radiation was the most important form of energy, and so the expansion rate dropped quickly. Later on, matter becomes more important than radiation, and so the expansion rate still drops, but less quickly than when radiation was the dominant player in the game. Just recently, dark energy became more important than even matter is, and so the expansion rate is now dropping very slowly: only the “matter and energy contributions” to the energy density are dropping. In the far future, when the matter and energy components become negligible, the energy density (which will be 100% due to dark energy) will remain constant, and the expansion rate will not only stop dropping, but that means the expansion will become exponential.

The scale of the Universe (y-axis) versus the age of the Universe (x-axis) on logarithmic scales. Some size and time milestones are marked, as appropriate. Everything contained within the entire observable Universe was once contained in a very small volume, as shown by the size scale on the y-axis.

If we were to follow how the Hubble constant changes over time — and yes, calling it the Hubble “constant” is tremendously stupid, especially when we have a much better term that we also use: the Hubble parameter — we’d find that it starts off large, drops and drops and drops, but then, when dark energy becomes dominant, it drops at a slower and slower rate. Instead of approaching zero, it asymptotes to a finite, positive value that’s determined by the dark energy density. In the far future, the Hubble parameter will reach a minimum value of between 55-60 km/s/Mpc; it will never drop lower than that.

So if the expansion rate, i.e., the Hubble parameter, isn’t increasing, what does it mean that “The expansion of the Universe is accelerating?”

It means that if you watch how a distant galaxy recedes from us, its apparent recession speed gets faster and faster as time goes on. In other words, individual objects appear to accelerate away from us, but the expansion rate itself is still dropping the entire time. If it were up to me, we’d talk about:

• accelerated galaxies/distant objects, not an accelerated expansion,
• a dropping (but not to zero) expansion rate, not an accelerating expansion,
• and a Hubble parameter, not a Hubble constant.

But I don’t get to decide what we call things; I just get to explain what they actually mean to you. Hopefully, now you have a better understanding of how the Universe expands and what it all means, and the next time someone asks you about it, you’ll remember where to send them: right here!

Send in your Ask Ethan questions to startswithabang at gmail dot com!