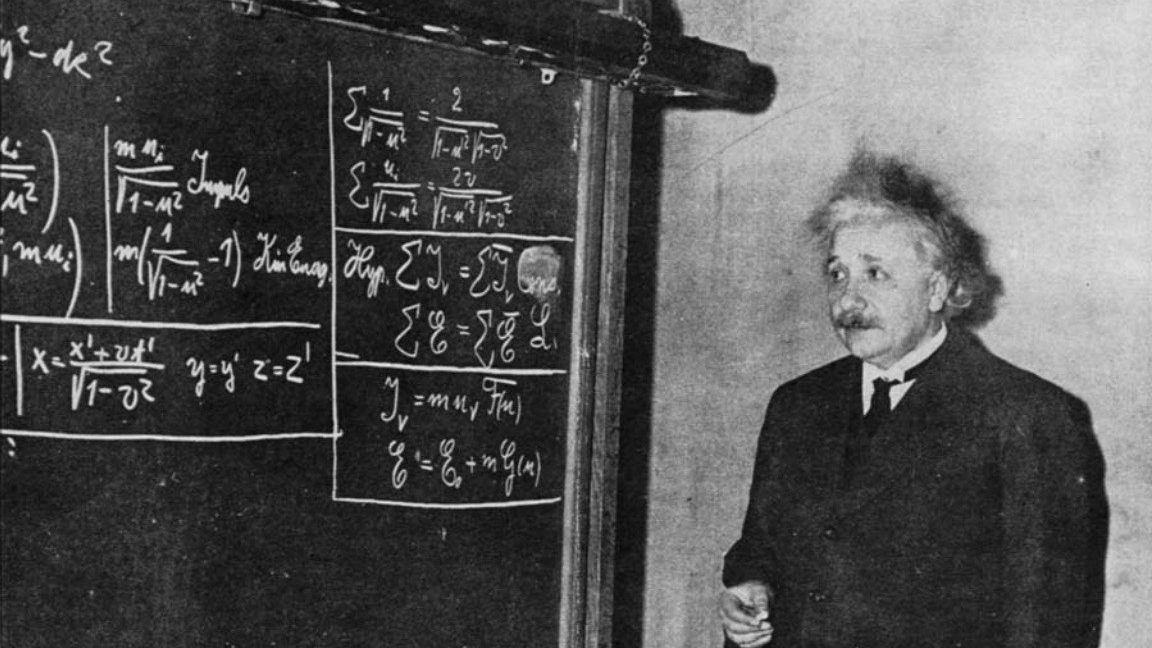This is the most important equation in cosmology
- If you want to understand the Universe, you have to reckon with all the complexity of General Relativity, including spatial curvature and the expansion of space.
- Although Hubble’s law, v = Hr, was the equation that established an observational basis for the expanding Universe, the Friedmann equations, derived years prior, provided the foundation for modern cosmology.
- Today, the first Friedmann equation is absolutely indispensable, from the Big Bang to dark energy and everything in between. Here’s why it’s cosmology’s most important equation.
Cosmology is the study of the Universe: from the smallest scales to the largest. If we want to understand this Universe we inhabit, we have no choice but to consider everything all together, from the subatomic particles that compose our reality to the largest-scale structures that they form. This requires understanding not only the various quanta that bind together and make up all that we can observe and interact with, but the proverbial stage upon which they move. The Universe doesn’t simply exist, but rather evolves with both space and time as our cosmic story unfolds.
It was barely a century ago — back in 1915 — that Einstein first unveiled the General theory of Relativity, which detailed how space-and-time affected the matter and energy within it, and how, conversely, the matter and energy within it determined the shape and evolution of spacetime. Remarkably, it would be just seven years later, a full 100 years ago at the time this article is being written, that the single most important equation in cosmology was first derived: the first Friedmann equation.
To a non-expert, it might seem like a travesty that the Friedmann equation, and not Hubble’s law, would be elevated to such an esteemed position. But to any expert, it’s the only choice worth considering. Here’s why.

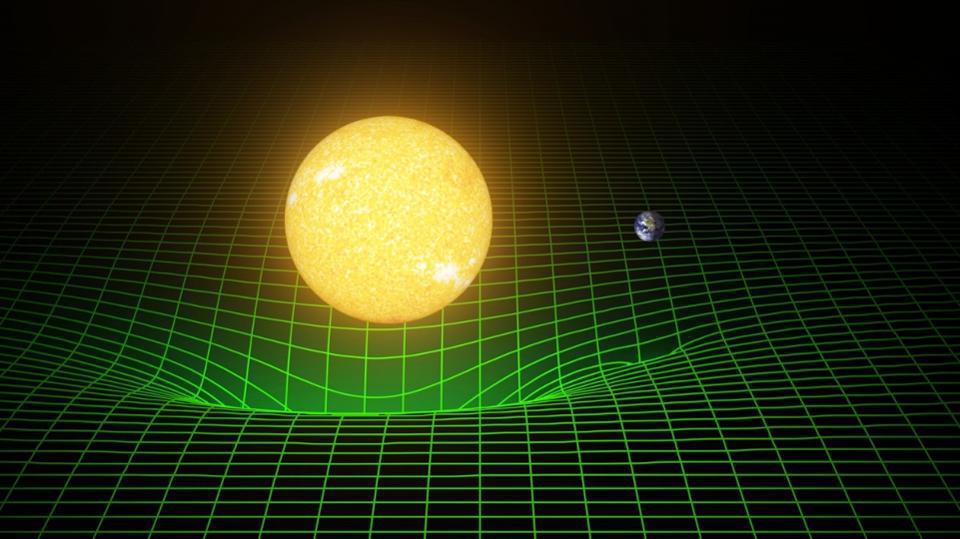
When it comes to the rules that govern the very fabric of the Universe, Einstein’s General Relativity is the only game in town. If you can write down how, at any moment in time, the matter-and-energy in the Universe is distributed, Einstein’s equations will tell you how the fabric of spacetime is curved at each and every location in the cosmos. Conversely, the curvature of spacetime, if you know it, will tell every quantum of matter-and-energy how to move within that Universe. It’s a complex dance, but the Einstein field equations are comprehensive enough to give us this information for any distribution of matter we can possibly imagine.
Of course, this system of 16 coupled equations — 10 of which are independent of one another — gets more and more difficult to write down, let alone solve, the more complicated the distribution of matter and energy is. If we make simplifying assumptions, however, we can sometimes come up with exact solutions for these idealized cases.
In all directions, everywhere that we look, we see that the Universe is roughly the same: there are stars and galaxies everywhere, in roughly the same numbers, in all locations and regions of space. If you imagine that the Universe as a whole has these properties — i.e., is isotropic (the same in all directions) and homogeneous (the same in all locations) — you can describe the global spacetime very simply. The structure of spacetime then leads directly to a set of equations that predict how the Universe will evolve: those are the Friedmann equations.

Very simply, the first of these equations has just four important terms in it, with each one having something important to say about a Universe that is — at least on the large-scale cosmic average — the same everywhere and in all directions.
- On the left-hand side, there’s a term that represents the change in the scale of the Universe divided by the scale of the Universe; this is the definition of the Hubble parameter, which governs how the Universe either expands or contracts over time.
- On the right-hand side, the first term represents all of the matter and energy that’s in the Universe in all its various forms: normal matter, dark matter, radiation, neutrinos, etc.
- The second term on the right-hand side represents the global curvature of spacetime, and dictates whether the Universe is open, closed, or spatially flat.
- And the third and final term on the right-hand side is Einstein’s cosmological constant, which dictates the energy that cannot be extricated from space itself.
What’s perhaps most remarkable about this equation, however, is its implications. If you have a Universe that’s filled, uniformly, with any type(s) of matter-and-energy, regardless of curvature or the value of the cosmological constant, then your Universe cannot be static. It must either expand or contract, and which one is happening is something you can only know by going out and measuring the Universe.
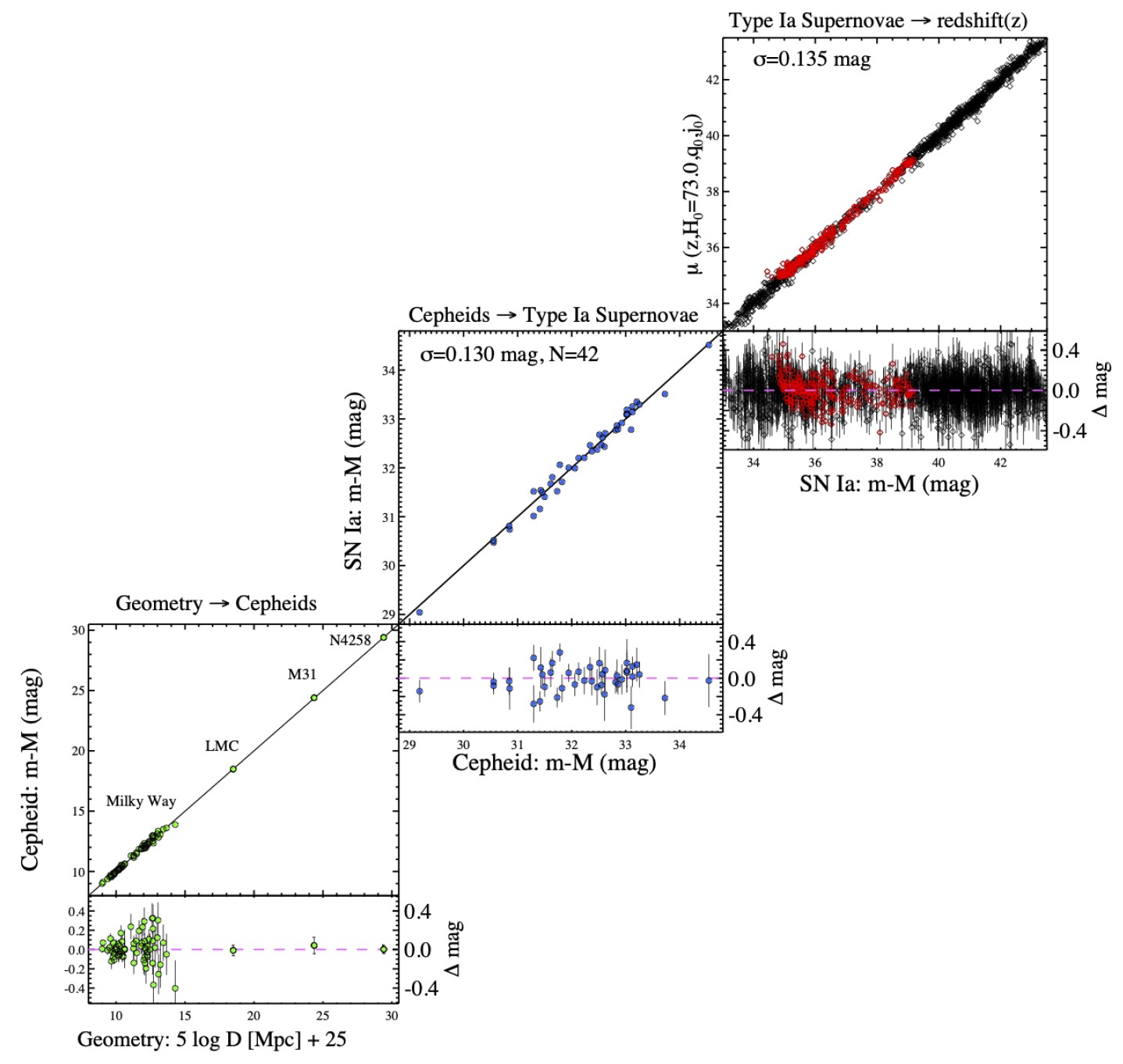
So let’s say you do that: you go out and measure the Universe. You measure the expansion-or-contraction rate right now, as well as how (or whether) it’s changed over time. You determine what the various types of matter and energy are present, and how much of each type there is. You measure the amount of spatial curvature, or you find that the Universe is flat to the limits of your measurement capabilities. And you measure the cosmological constant as well, which behaves identically to a form of energy whose energy density remains constant, irrespective of how the scale of the Universe evolves with time.
What else does this Friedmann equation give you?
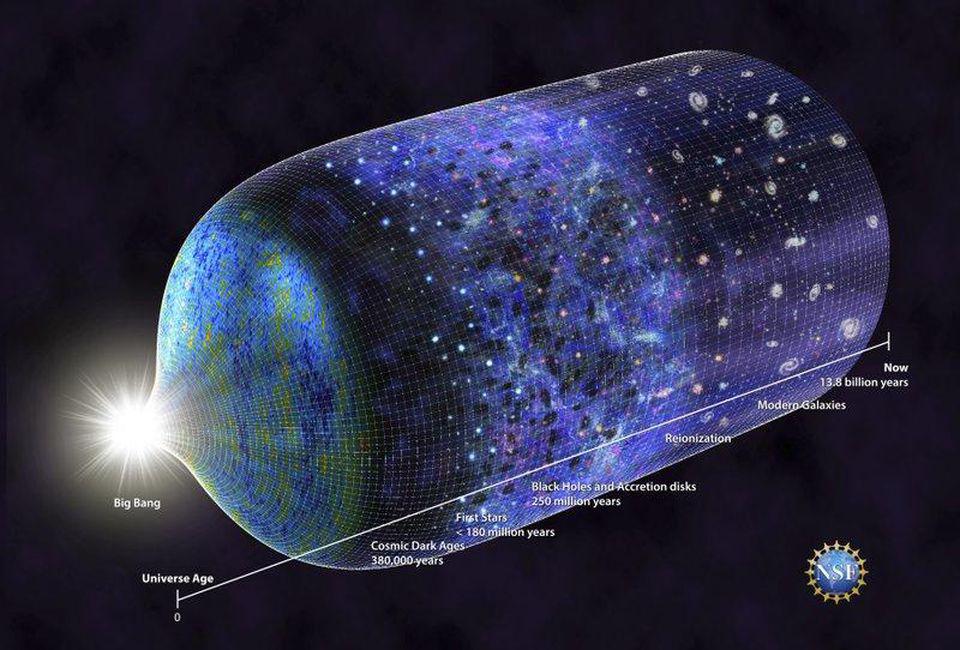
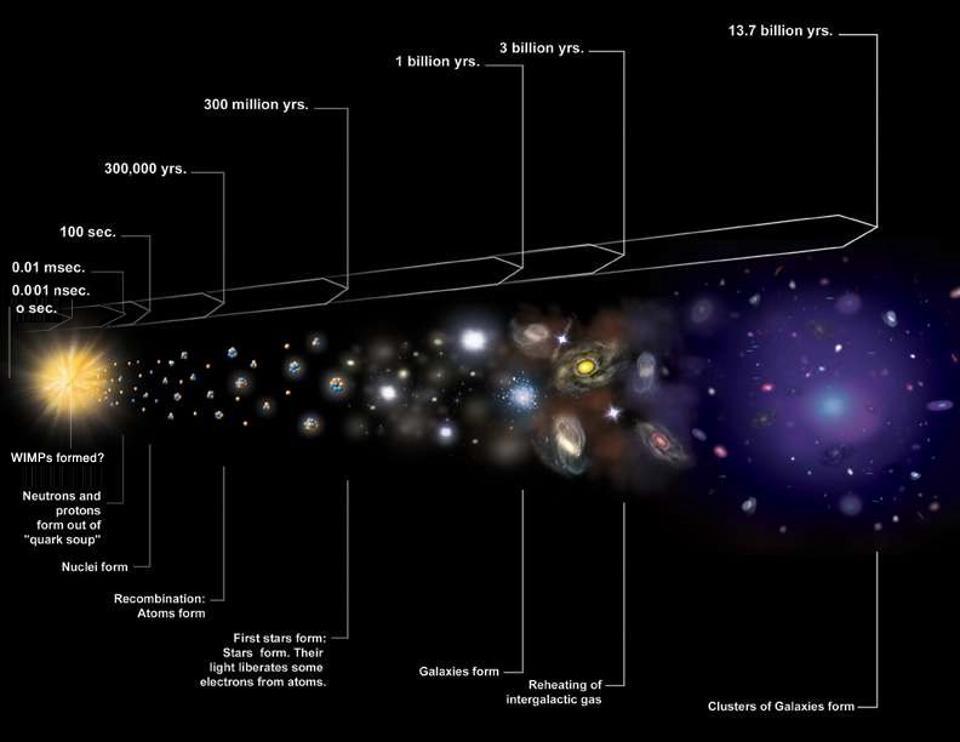
The entire history of the Universe, both past and future. It allows you to infer, if the Universe is expanding, how hot and dense things were at any point in the Universe’s past. If you have radiation, it allows you to infer when:
- it became too hot to form neutral atoms,
- it became too hot to form atomic nuclei,
- it became too hot to have individual protons and neutrons,
- the Universe spontaneously created matter/antimatter pairs,
and even to conclude that the Universe started off from a hot, dense, rapidly expanding state: what we call the hot Big Bang today.
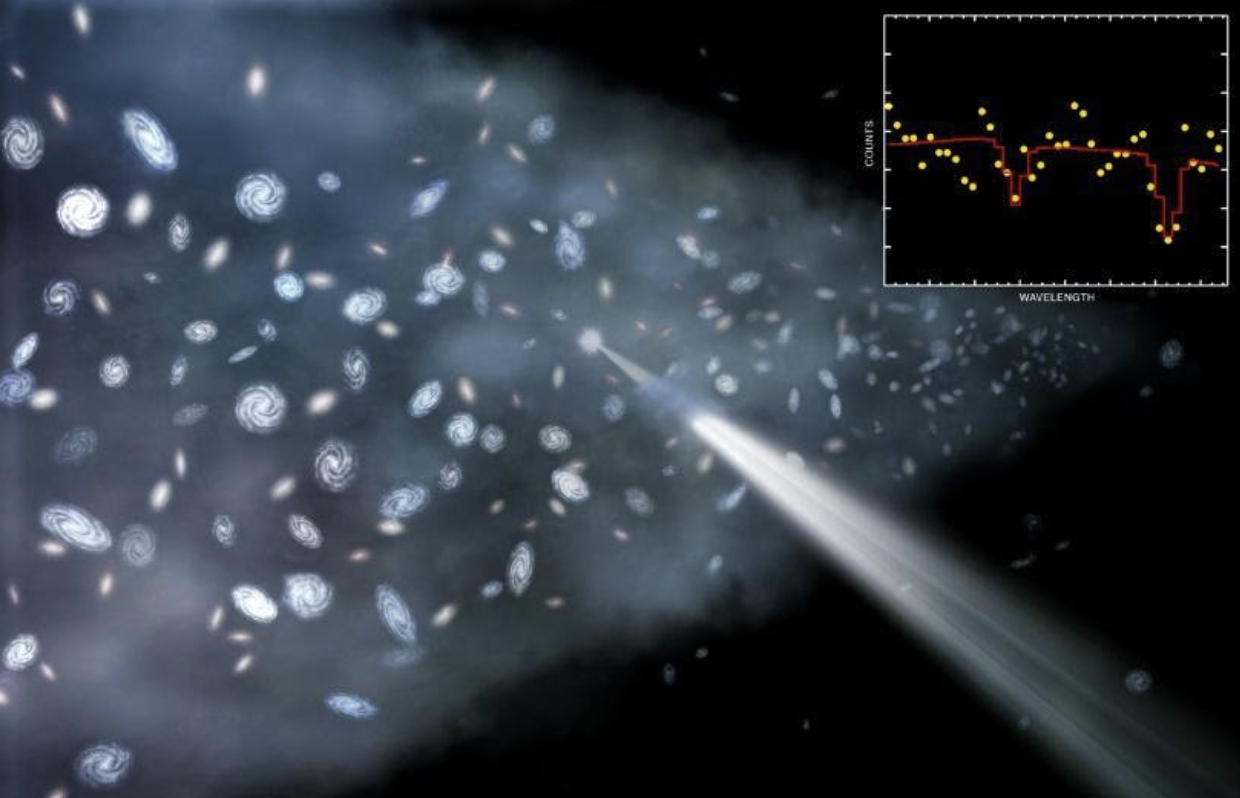
The first Friedmann equation also allows you to quantify how significantly the light from a distant object will be redshifted (or blueshifted) in an expanding (or contracting) Universe. If you know the rate of expansion (or contraction) and the intrinsic quantum mechanical properties of atoms, then you can go out and measure a distant object and calculate how severely the light will be affected by the evolution of the spacetime within the Universe.
This is what we call Hubble’s law. In other words, although Hubble’s law was empirically derived — that is, it was determined from observations alone, irrespective of the underlying theory — it can be derived theoretically solely from this all-important equation.
Although it was Hubble who first measured the distances to galaxies outside of the Milky Way, it was a much lesser-known astrophysicist, Georges Lemaître, who first put all of the pieces together about our cosmic origins. Working within the framework of the Friedmann equations and pulling the early published distance data from Hubble, his associate Humason, along with the redshift data from earlier observations made by Vesto Slipher, Lemaître:
- derived Hubble’s law,
- made the first estimate for the rate of expansion of the Universe,
- and put forth the startling conclusion that the Universe was not eternal, but rather began a finite amount of time ago with a hot Big Bang.
That was back in 1927, and after sending a letter about his conclusions to Einstein, who sent back a legendarily dismissive (and incorrect) response that his, “mathematics was correct, but [his] physics was abominable,” it would fall to Howard Robertson (in 1928) and finally, to much fanfare, Hubble himself in 1929, to bring the idea of the expanding Universe into the mainstream.

In a similar fashion, the first Friedmann equation can also be used to evolve the Universe forward in time. You have to understand that the most powerful type of equation in all of physics is a differential equation, and that’s precisely what the first Friedmann equation is.
Why are differential equations so important?
Because those are the types of equations that enable you, if you know how any physical system behaves at any one particular moment, to evolve your system either forward or backward in time: to either the next moment or the previous moment. But the true power of a differential equation can be seen when you make it to either that subsequent or preceding moment, because it’s that very same equation, only with the new values for the system’s physical properties at that time, that will tell you again what happens in either the next or prior moment.
The first Friedmann equation, therefore, enables you to both trace the Universe’s history back in time for as long as that equation applies, and also forward in time in the same fashion. Assuming there are no abrupt, colossal changes in the types of energy that make up the Universe, measuring the Universe as it is today allows us to conclude what its ultimate fate will be.

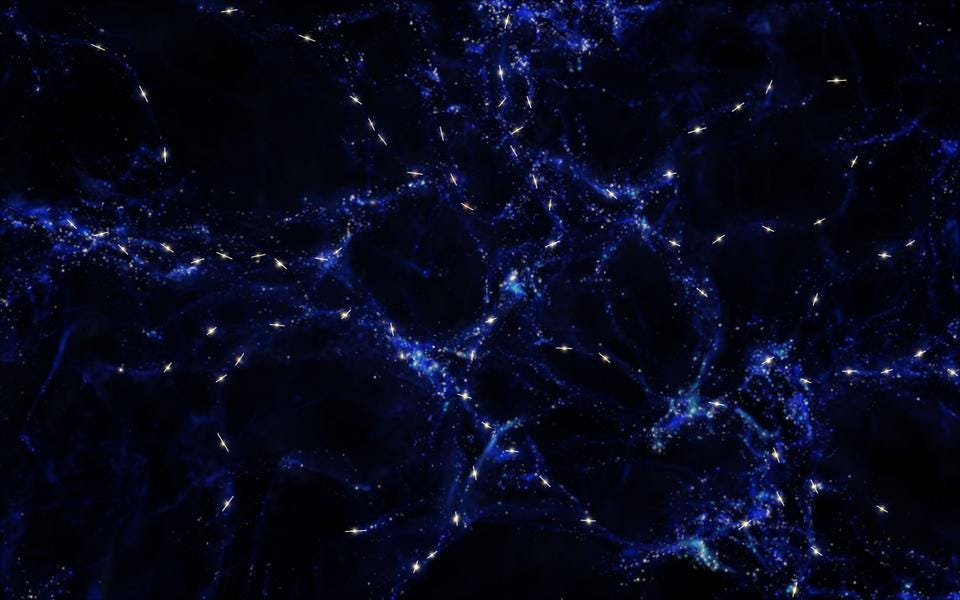
And still, even with all of that, the first Friedmann equation isn’t done. On average — on the largest of cosmic scales — the Universe really is isotropic and homogeneous. If you were to draw a sphere, say, of ~10 billion light-years in diameter, around any region of our observable Universe, you’d enclose only about 0.1% of the volume of the visible Universe. And yet, whether you drew that sphere around the densest galaxy cluster in the cosmos or the sparsest cosmic void, if you added up all the matter-and-energy inside that sphere, you’d get the same precise value to ~99.99% precision. The Universe, on the largest scales, is uniform to a whopping 1-part-in-30,000.
But if you go down to small cosmic scales, to things like galaxy clusters, galactic groups, individual galaxies, or even smaller to star clusters, individual stellar systems, or even to isolated stars and/or planets, you’ll find that the Universe is remarkably non-uniform.
Guess what?
The first Friedmann equation allows you to derive it. It allows you to derive and quantify the level of non-uniformity — the departure from isotropy and homogeneity — on any cosmic scale at any time. By adding in inhomogeneous (i.e., non-uniform) perturbations atop the otherwise uniform background, we can derive the presence and growth of cosmic structure.

There are a number of people who, way back in the day, worried that the assumption of uniformity in the Universe wasn’t a good one. There are still a bunch of physicists, albeit very few working astrophysicists on either the theoretical or observational sides, who worry that the Universe might be too inhomogeneous for the first Friedmann equation to apply to our Universe as it actually is.
The thing is, if you’re worried about that, there are questions you should legitimately be asking.
- Is there a preferred frame of reference?
- Do galaxies rotate clockwise more frequently than they rotate counterclockwise?
- Is there evidence that quasars only exist at multiples of a specific redshift?
- Does the cosmic microwave background radiation deviate from a blackbody spectrum?
- Are there structures that are too large to explain in a universe that is, on average, uniform?
Although most of those who question the homogeneity of the Universe refuse to admit it, the truth is that we check and test these assumptions all the time. To make a long story short, despite the occasional assertion that some large inhomogeneity persists, there are none that have ever held up to scrutiny.
The only frame of reference that’s notable is the one where the Big Bang’s leftover glow appears uniform in temperature. Galaxies are just as likely to be “left-handed” as “right-handed.” Quasar redshifts are definitively not quantized. The radiation from the cosmic microwave background is the most perfect blackbody we’ve ever measured. And the large quasar groups we’ve discovered are likely to only be pseudo-structures, and not gravitationally bound together in any meaningful sense.
If the first Friedmann equation is valid, then not only can we determine both the origin and the fate of our Universe, but we can derive all sorts of properties about the Universe at any moment in time.
- We can determine what the relative importance of all the different forms of matter and energy were and will be at any point in cosmic history.
- We can determine the absolute density of each component of the Universe at any moment in our cosmic history.
- We can determine both the expansion rate and the change in the expansion rate over time at any moment in cosmic history.
- We can determine all the different “epochs” that our Universe went through, including when it was dominated by radiation, by dark matter, and by dark energy.
And if there had been other components of the Universe that ever dominated, such as neutrinos, normal matter, cosmic strings, or something even more exotic, we’d be able to determine that, too. Observationally, we can derive how large an object would appear or how bright it would seem based on how far away it was when it emitted its light within the expanding Universe. Pretty much any property you’d want to know — redshift, distance, expansion rate, lookback time, etc. — can be derived from little more than this one equation, alone.

Of course, there are limits to what the first Friedmann equation can do. It cannot smoothly describe what happens in regions of space that aren’t expanding any longer, such as gravitationally bound structures like galaxies and galaxy groups. Also, it cannot smoothly describe what happened when there were abrupt transitions in the energy contents of the Universe, such as at the end of inflation and the onset of the hot Big Bang. But from the earliest moments where the hot Big Bang applies to as far into the future as we believe ourselves capable of extrapolating, the first Friedmann equation truly is the most important equation in all the Universe.
The Friedmann equations, and in particular the first Friedmann equation — which relates the Universe’s expansion rate to the sum total of all the different forms of matter and energy within it — has been known for a full 100 years, while humans have applied to the Universe for almost as long. It’s shown us how the Universe has expanded over its history, and enables us to predict what our ultimate cosmic fate will be, even in the ultra-distant future.
But we can only be certain our conclusions are correct to a particular level of confidence; if there’s an abrupt change in the contents of the Universe, then any conclusions we’ve drawn about our future are no longer certain. Beyond the limitations of our data, we must always remain skeptical of drawing even the most compelling conclusions. Beyond the known, our best predictions can only remain mere speculations.