How much energy does the Sun produce?

When it comes to planet Earth, the most important source of light, heat, and energy actually comes from beyond our world. It’s the Sun that is the driver of the Earth’s energy balance, rather than the internal heat given off by the planet itself from sources like gravitational contraction and radioactive decays. The energy from the Sun keeps temperatures from freezing all across the planet, providing us with temperatures that allow liquid water on Earth’s surface, and that are essential to the life processes of nearly every organism extant on our world today.

And yet, it’s only within the last 200 years that humanity has even understood how much energy, overall, the Sun actually produces. Considering all of the scientific advances that came afterward, including the development of stellar, quantum, and nuclear physics, as well as the understanding of the subatomic fusion reactions that power the Sun, it might seem like a trivial matter to simply answer the question of “How much energy does the Sun produce?” But looks can be deceiving. If you didn’t already know (or hadn’t already googled) the answer to that question, how would you figure it out? Here’s how humanity did it.

When sunlight strikes the Earth’s surface, it has already been processed: by not only its journey from the Sun to the Earth, but by Earth’s atmosphere, clouds, and all objects that absorb or emit light along its journey to us. Here’s how we did our best to overcome those limitations and measure the Sun’s power output.

The Solar System is not enough

You might think to yourself that simply knowing a few physical properties about the Sun, such as:

• how big it is,
• how massive it is,
• and how far away from Earth it is,

would go a long way toward delivering the answer to such a question. After all, with even extremely primitive tools (like your naked eye and a sextant), you can determine how large, in terms of angular size, the Sun is. Since ancient times, it’s been known that the Sun is approximately half-a-degree across from end-to-end, with more modern measurements confirming that its angular size varies from 31.46 to 32.53 arcminutes over the course of a year. (Where 60 arcminutes equates to one degree.)

But that’s approximately the same angular size that the Moon takes up, and one is very close and relatively small while the other one is enormous and much farther away. We’ve been able to know the Moon’s size for around 2000 years, because once you know the size and shape of the Earth, viewing the Earth’s shadow on the Moon (during the partial phases of a lunar eclipse) allows you to infer the Moon’s size relative to the Earth. With just a little bit of geometry, you can then figure out the physical size of the Moon. This method was first used by Aristarchus in the 3rd century B.C.E., but it’s of no help in determining the distance to the Sun.

Animation showing the umbral phase of the November 19, 2021 partial lunar eclipse. At 9:03 AM UT, maximum eclipse is reached, where only 0.9% of the Moon remains illuminated by direct sunlight. The umbral phase lasts over 3.5 hours: the longest this century for a partial eclipse. Reconstructing the size of Earth’s shadow relative to the physical size of the Moon is the oldest method for measuring both the size of the Moon as well as the distance to it: a method first leveraged by Aristarchus back in the 3rd Century BCE.

The next great leap in determining the physical properties of the Sun wouldn’t arrive until the 17th century, when first Kepler and then Newton came along to put the Solar System in order. By determining the orbital dynamics of the planets, Kepler was able to arrive at three important laws that governed the planets’ motions around the Sun.

1. Planets move about the Sun in elliptical orbits, with the Sun at one focus of that ellipse.
2. Planets sweep out equal areas in equal times with respect to the Sun, moving more rapidly close to perihelion and more slowly close to aphelion.
3. And the square of a planet’s orbital period is proportional to the cube of the semimajor axis of the ellipse that its orbit traces out.

When Newton came along toward the end of the 17th century and put forth his law of universal gravitation, he placed Kepler’s qualitative and proportional laws of motion onto a more solid, quantitative mathematical footing. By introducing the notion of a universal gravitational constant and by showing that gravity was consistent with obeying an inverse-square force law, Newton finally, based on the measurement that Earth’s orbit takes one year to complete, gave us an accurate way to measure the distance to the Sun.

While all of the planets in the Solar System orbit the Sun in the same direction, Venus, uniquely, rotates in the opposite direction. For each orbit completed by Venus, although it is the slowest-rotating planet, it experiences roughly two “days” of sunrises and sunsets.

Measuring the distance to the Sun gave us a vitally important piece of information, as we now know, based on the already-measured angular size of the Sun, how physically large it must be. Since the Sun is a sphere — the most perfect sphere in the Solar System, in fact — knowing its distance and angular size tells us its radius and, therefore, its surface area. The only piece of information that was left ambiguous was its mass, as Newton’s laws could only give us the product of his universal gravitational constant, G, and some particular mass (like the mass of the Sun or Earth), but was unable to disentangle them. That advance wouldn’t arrive until 1798, when Henry Cavendish was able to experimentally measure the gravitational constant directly.

If we want to know how much energy the Sun produces, knowing the distance from the Earth to the Sun is a huge asset, since we know how sunlight (like all forms of light) spreads out: like the surface area of a sphere. At double the distance, the Sun’s incident energy on a target will be quartered. Based on how much of the Sun’s energy is absorbed at the distance of Earth over a particular area, we can then calculate the total energy (and power) outputted by the Sun. Knowing all about the Solar System can get us very far in the quest to measure the Sun’s energy output, but measurements here on Earth are still needed.

The way that light spreads out as a function of distance means that the farther away from a power source you are, the energy that you intercept drops off as one over the distance squared. This also illustrates, if you view a certain specific angular area (illustrated by the squares) from the perspective of the original source, how larger objects at greater distances will appear to take up the same angular size in the sky. Each time you double your distance between a source and observer, the brightness you observe gets quartered. In general, photons (and all light) propagate spherically outward away from the emitting source.

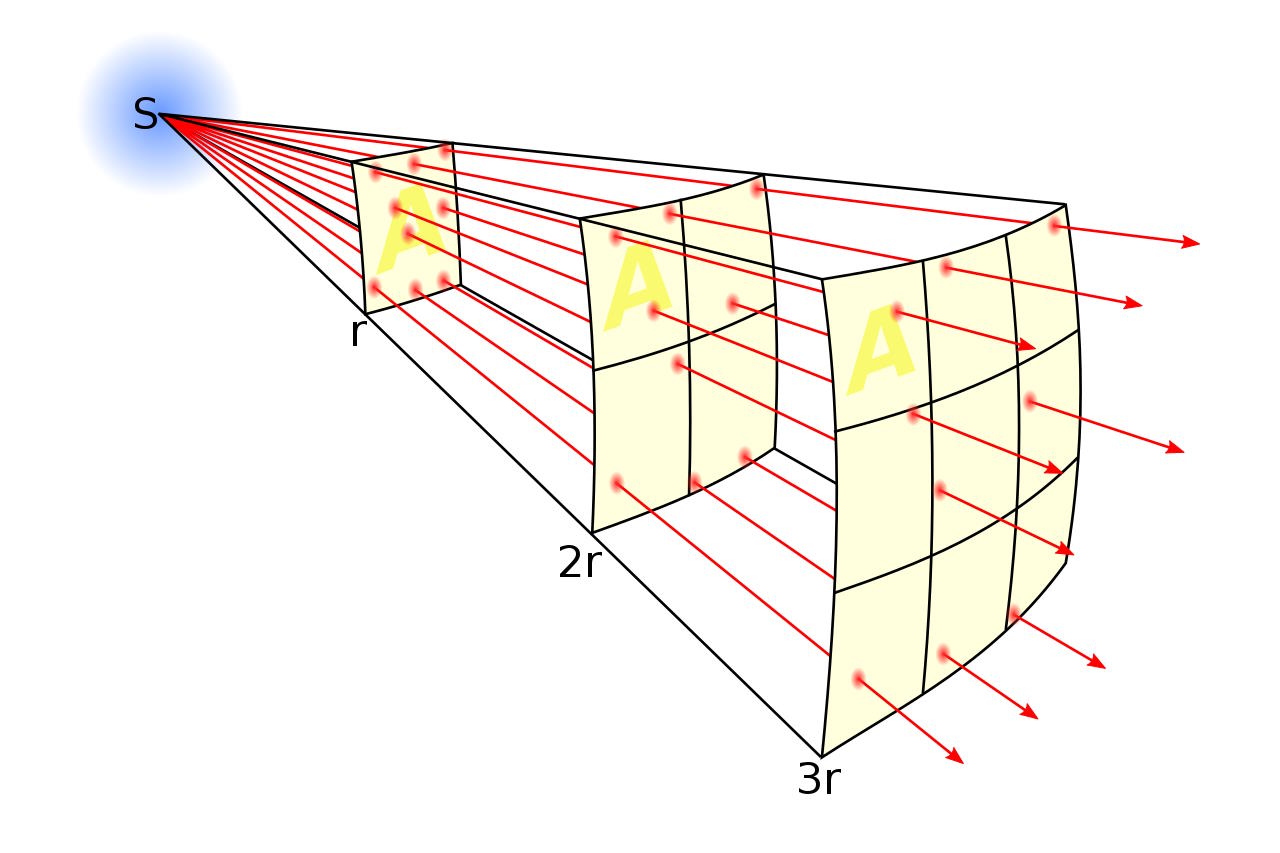
Sunlight is more than visible light

Today, we take for granted that there’s much more to light than the tiny portion of the spectrum that’s visible to our eyes. But back hundreds of years ago, this wasn’t obvious in any easily provable way. Hot objects, which today we know emit large amounts of infrared radiation, were thought to possess a quantity of heat energy that had no light-based counterparts. At high energies, gamma-rays, X-rays, and ultraviolet light were not known, while at longer wavelengths and lower energies, there was not yet evidence for microwave or radio waves.

The first evidence for the existence of light beyond visible light — especially for light beyond the visible part of the spectrum as being part of sunlight — was uncovered quite by accident. Astronomer William Herschel, the famed discoverer of Uranus (which he found in 1781), suddenly found himself the recipient of accolades, resources, and wealth: largely gifted by King George III of England. He began to devote himself to astronomy full-time, completing what was then the world’s largest telescope later in the 1780s, discovering Titania and Oberon in 1787 (Uranus’s two largest moons), and then turned his attention to another astronomical object of interest: the Sun.

The behavior of a beam of sunlight, perhaps the greatest example of white light, as it passes through a prism demonstrates how light of different energies moves at different speeds through a medium, but how they all move at the same speed through a vacuum, which is why the light that doesn’t pass through a refractive medium remains white in color. Note that the visible light shown here is only illustrative of the sunlight that we can see; other wavelengths of light still exist beyond the portion that’s visible.

Herschel was extremely interested in viewing the Sun directly, but was aware of the damage (and pain) it could cause to one’s eyes. He was aware that through a telescope, the magnified light would significantly amplify the damage it could cause, but that by passing that light through a filter, he could reduce the intensity of the light his eyes would receive. In 1794, he presented a paper to the Royal Society where he recorded his experience viewing the Sun (and other stars), with a telescope but with a variety of filters applied.

He noted, quite remarkably, that:

• some of the filters greatly reduced the amount of light emitted by the Sun, but did little to alter its sensation of heat,
• some of the filters greatly reduced the amount of heat felt from the Sun, but did little to reduce the amount of visible light,
• and some filters greatly reduced both.

Herschel then speculated that both the heating power and the illuminating power of various colors of sunlight might be different from one another. To test this out, Herschel built what astronomers know today as a spectrometer: a device to break up light into its component wavelengths, where he could measure how much power-and-energy were inherent to each individual wavelength, which corresponded to the colors he could see.

The three types of cone cells found in human eyes, S, M, and L, shown with the wavelength range that they respond to: short, medium, and long wavelengths. Some humans lack one type of cone, rendering them color blind, while a few people have four types of cones and can see more colors than the rest of us: tetrachromats. The greatest sensitivity of human eyes to the intensity of light occurs between 500 and 600 nanometers, with the response dropping off rapidly at the most extreme red and violet wavelengths.

It was in 1800 that Herschel set up this spectrometer and shone sunlight through it, with the prism-like effect of the spectrometer creating a beautiful rainbow of colors. He would then set up a slit to allow a narrow range of color wavelengths through, where that light would fall onto a thermometer. Right next to it, but in complete shadow of this light, was the “control” thermometer. By observing the difference in temperatures induced by the light, Herschel was able to say something about the “heating power” of the various colors of light, which told him something about the overall energy.

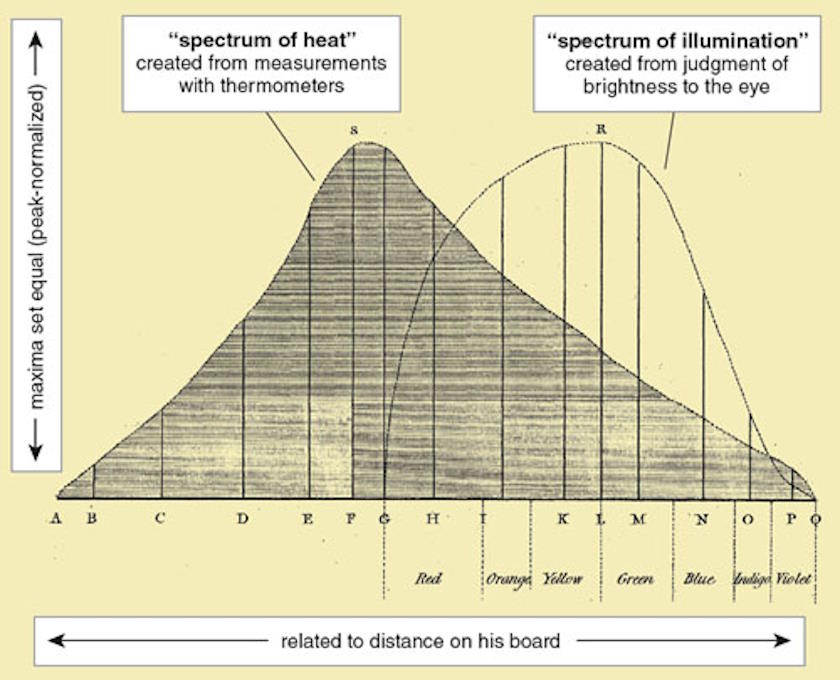
He quantified how violet, green, and red light behaved, among others, and noted that heating increased for redder colors of light as compared to the bluer colors. He then went further: beyond where the visible light portion of the spectrum ended. Lo and behold, even as the light was no longer visible, the heating continued to increase: demonstrating the presence of invisible light, in the form of what we today call infrared radiation. Herschel’s data was good enough that he was even able to measure the spectral intensity of infrared radiation, including its peak and subsequent fall-off. The data from his final paper on the topic, written in 1800, is shown below, with annotations by Jack White.

This graph shows the intensity of visible light, by brightness, as a function of color on the right, while the shaded region shows the temperature-recorded heat intensity of light at both visible and infrared wavelengths. This 1800 publication, by William Herschel, represented the most robust demonstration of the existence of “invisible light” at the time.

Solving for the power of the Sun

But how much energy, total, was coming from the Sun? It was not yet generally accepted that light was a wave, so the correspondence of color with wavelength wasn’t known. With that modern knowledge, we know that the crown glass crystal that Herschel used likely absorbed a significant amount of shorter-wavelength light, and that the human eye responds much more severely to yellow and green wavelengths of light than to red wavelengths, implying that his measurements were not solely measuring the energy coming from the Sun, and certainly not in an unbiased way.

But we could imagine how that energy could be measured, and in fact two people put forth the idea: John Herschel, William’s son, and Claude Pouillet. All you had to do, they reasoned, was:

• create an open vessel that was filled with a high specific-heat material that was a good absorber of heat, like water,
• that would be held within a highly reflective material, like silver, that reflected sunlight of all wavelengths equally well,
• along with a device for measuring heat/temperature gain (like a thermometer),
• plus a way to calculate heat losses and dispersion from atmospheric effects,

and you could then infer how much energy was in sunlight incident on that particular area. Imagine expanding that area to the size of Earth’s orbit around the Sun, and you can calculate the energy emitted by the entire Sun itself.

This schematic drawing shows an actinometer developed by Jules Violle, which was intended to deduce the temperature of the Sun at its surface. Building upon earlier designs, including those of Pouillet and Herschel, allowed us to not only measure the total power-per-square-meter arriving from the Sun, but more intricate properties as well.

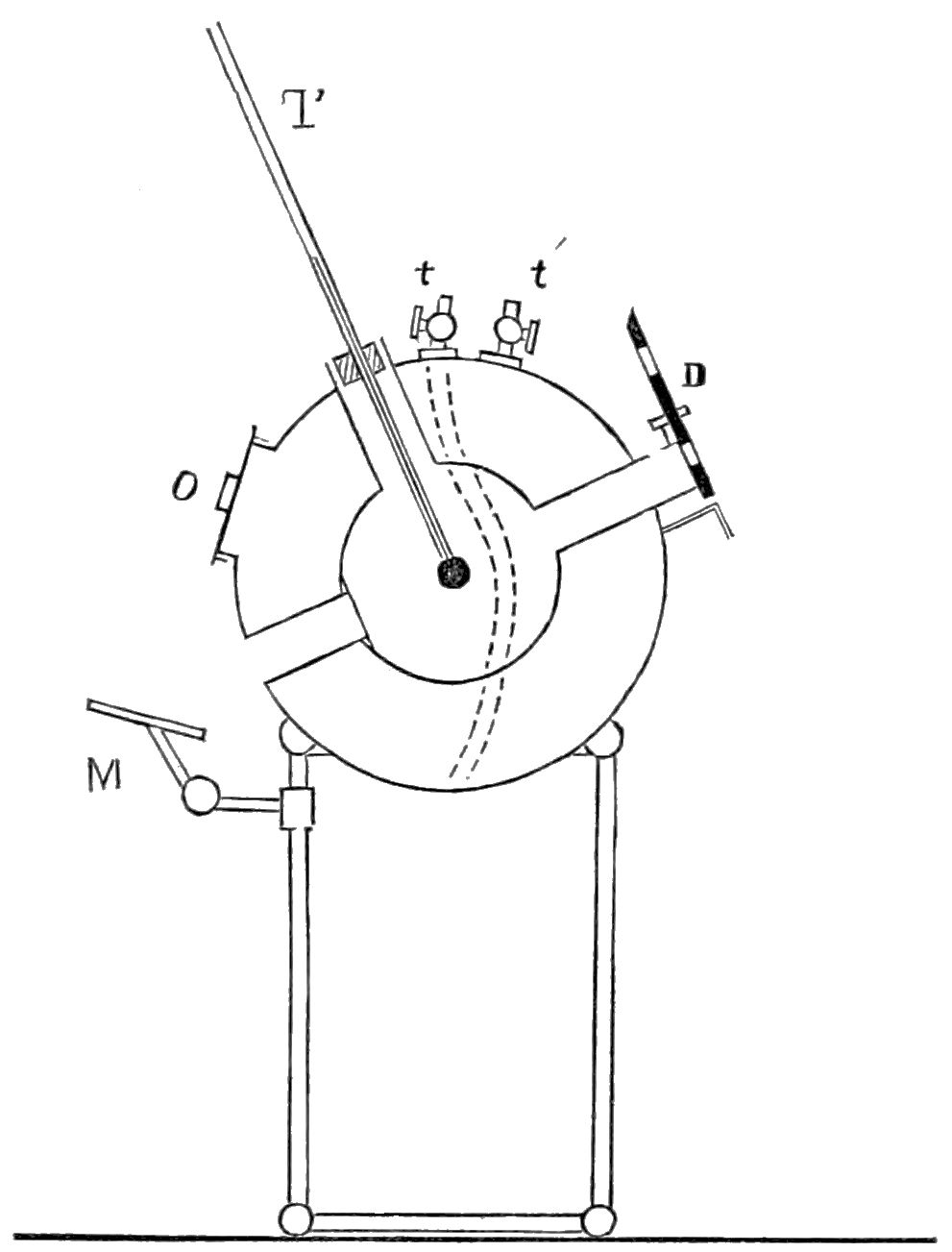
The earliest device that could do this, developed by John Herschel in 1825 (just three years after his father, William, passed away), was known as an actinometer. In 1833, Herschel traveled to South Africa for several years, and there was using reflective materials to build his own solar cooker, which proved much more effective at the near-equatorial latitudes in South Africa as compared to those back at home in England (33° to 51°, for comparison). Because the Earth is tilted on its axis by 23.5°, Herschel realized that he would have an incredible opportunity in South Africa that he wouldn’t have in England: to observe the Sun when it was nearly directly overhead, during the December solstice.

He brought his actinometer out and performed the experiment: setting up this initially cool-water vessel (kept in the shade) until the Sun was almost perfect overhead, at midday on the solstice. Then, he removed the shade, and watched the temperature rise during those critical moments, allowing him to calculate the energy output by the Sun over the time that the water was heated. Energy over time, in physics, is what’s known as power, and Herschel’s measurement worked out to a little more than one kilowatt of solar energy for each square meter of Earth that sunlight strikes.

This image of the Sun, taken on April 20, 2015, shows a number of features common to all stars: magnetic loops, prominences, plasma filaments, and regions of higher and lower temperatures. However, the slowly-rotating Sun is the most perfect sphere in the Solar System, with a polar and equatorial diameter that are identical to 99.9993% precision.

By extrapolating the surface area over which sunlight struck his container to cover the total amount of sky at Earth’s orbital distance from the Sun, Herschel was able, for the first time, to estimate the outputted power of the Sun itself: that value works out to somewhere around 4 × 10²⁶ watts. (Herschel’s value was a little bit lower, as he underestimated the amount absorbed/reflected by the atmosphere.) That means, with each second that goes by, the Sun:

• fuses around 10³⁸ protons within its core into heavier elements,
• transforms 620 million tonnes of hydrogen,
• into 616 million tonnes of helium,
• and releases the energy-equivalent of 4 million tonnes of matter via Einstein’s E = mc².

It turns out that even though the Sun’s peak wavelength occurs in the visible light portion of the spectrum, the majority of the Sun’s total energy really is emitted at infrared wavelengths. This technology was swiftly put to use. By 1870, sunlight was used to create the first solar-powered motors, which developed into different engine configurations and became more efficient throughout the decade. By 1880, the first solar cell was developed, and in the 1950s, NASA began using solar power in space. All of today’s modern applications of solar power rely on knowing how much energy is outputted by the Sun, a piece of knowledge that’s less than 200 years old. Remarkably, now you know how to figure that value out for yourself!