The biggest difference between physics and mathematics

To an outsider, physics and mathematics might appear to be almost identical disciplines. Particularly at the frontiers of theoretical physics, where a very deep knowledge of extraordinarily advanced mathematics is required to grasp even cutting-edge physics from a century ago — curved four-dimensional spacetimes and probabilistic wavefunctions among them — it’s clear that predictive mathematical models are at the core of science. Since physics is at the fundamental core of the entire scientific endeavor, it’s very clear that there’s a close relationship between mathematics and all of science.

Yes, mathematics has been incredibly successful at describing the Universe that we inhabit. And yes, many mathematical advances have led to the exploration of new physical possibilities that have relied on those very advances to provide a mathematical foundation. But there’s an extraordinary difference between physics and mathematics that one of the simplest questions we can ask will illustrate:

• What is the square root of 4?

I bet you think you know the answer, and in all honesty, you probably do: it’s 2, right?

I can’t blame you for that answer, and it’s not exactly wrong. But there’s much more to the story, as you’re about to find out.

A ball in mid-bounce, as shown here, could be moving to the right and losing energy with each successive bounce, or could be moving to the left and gaining energy with each successive bounce. While Newton’s laws of motion are the same whether you run the clock forward or backward in time, not all of the rules of physics behave identically if you run the clock forward or backward.

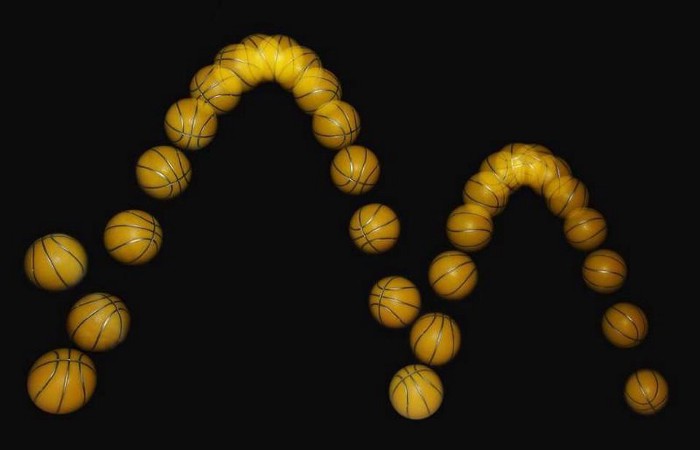
Take a look at the above time-lapse image of a bouncing ball. One look at this tells you a simple, straightforward story.

1. The ball starts off on the left side of the image, where it’s clearly been dropped with some speed while also moving to the right.
2. The ball bounces while continuing to move to the right, accelerating downward due to gravity, reaching a maximum height and then falling back down to the floor again.
3. That collision with the floor robs the ball of some of its kinetic energy, but it still bounces upward, continuing to rise (but to a lesser height than after the previous bounce) and move to the right, while gravity accelerates it back down toward the floor.
4. And, if we were continue to monitor this ball, we’d find that it would move to the right, while continuing on in a series of bounces, with each successive bounce taking it to a lesser and lesser height until it ceased bouncing altogether, remaining on the floor and rolling until it comes to rest.

This is, quite reasonably, the story you’d tell yourself of what’s going on.

But why, may I ask, would you tell yourself that story rather than the opposite: that the ball begins on the right side, moving leftward, and that it gains energy, height, and speed after each successive “bounce” on the floor?

In Newtonian (or Einsteinian) mechanics, a system will evolve over time according to completely deterministic equations, which should mean that if you can know the initial conditions (like positions and momenta) for everything in your system, you should be able to evolve it, with no errors, arbitrarily forward in time. One cannot describe the position of an object accurately without including a time coordinate in addition to the spatial ones. In our practical Universe, due to the inability to know the initial conditions to truly arbitrary precisions, including when we factor in the presence of quantum uncertainty, this is not true to arbitrary accuracy.

The only answer you’d likely be able to give, and you may find it dissatisfying even as you give it, is your experience with the actual world. Basketballs, when they bounce, lose a percentage of their initial (kinetic) energy upon striking the floor; you’d have to have a specially prepared system designed to “kick” the ball to higher (kinetic) energies to successfully engineer the alternate possibility. It’s your knowledge of physical reality, and your assumption that what you’re observing is aligned with your experiences, that lead you to that conclusion.

Similarly, look at the diagram, above, that shows three stars all orbiting around a central mass: a supermassive black hole. If this were a movie, instead of a diagram, you could imagine that all three stars are moving clockwise, that two move clockwise while one moves counterclockwise, that one moves clockwise and two move counterclockwise, or that all three move counterclockwise.

But now, ask yourself this: how would you know whether the movie were running forward in time or backward in time? In the case of gravity — just as in the case of electromagnetism or the strong nuclear force — you’d have no way of knowing. For these forces, the laws of physics are time symmetric: the same forward in time as they are backward in time.

Individual protons and neutrons are colorless entities: the only type of quark state admissible in the Universe today. Although the strong force is mediated by massless (gluon) particles, the only force that exists between individual bound states are due to mesons, which themselves are all quite massive, limiting the strong force’s range severely.

Time is an interesting consideration in physics, because while the mathematics offers a set of possible solutions for how a system will evolve, the physical constraint that we have — time possesses an arrow, and always progresses forward, never backward — ensures that only one solution describes our physical reality: the solution that evolves the system forward in time. Similarly, if we ask the opposite question of “What was the system doing in the lead-up until the present moment?” the same constraint, that time only moves forward, enables us to choose the mathematical solution that describes how the system was behaving at some prior time.

Consider what this means, then: even given the laws that describe a system, and the conditions that the system possesses at any particular moment, the mathematics is capable of offering multiple different solutions to any problem that we can pose. If we look at a runner, and ask, “When will the runner’s left foot strike the ground?” we’re going to find multiple mathematical solutions, corresponding to the many times their left foot struck the ground in the past, as well as many times their left foot will strike the ground in the future. Mathematics gives you the set of possible solutions, but it doesn’t tell you which one is “the right one.”

Having your camera anticipate the motion of objects through time is just one practical application of the idea of time-as-a-dimension. For any set of conditions that will be recorded throughout time, it’s plausible to predict when a certain set of spatial conditions (including position and velocity) will arise, with multiple possible solutions being admissible for both the past and future.

But physics does. Physics can allow you to find the correct, physically relevant solution, whereas mathematics can only give you the set of possible outcomes. When you find a ball in mid-flight and know its trajectory perfectly well, you have to turn to the mathematical formulation of the physical laws that govern the system to determine what happens next.

You write down the set of equations that describe the ball’s motion, you manipulate and solve them, and then you plug in the specific values that describe the conditions of your particular system. When you work the mathematics that describe that system to its logical conclusion, that exercise will give you (at least) two possible solutions as to precisely when-and-where it will hit the ground in the future.

One of those solutions does, indeed, correspond to the solution you’re looking for. It will tell you, at a particular point in the future, when the projectile will first strike the ground, and what its positions will be in all three spatial dimensions when that occurs.

But there will be another solution that corresponds to a negative time: a time in the past where the projectile would also have struck the ground. (You can also find the 3D spatial position of where that projectile would be at that time, if you like.) Both solutions have equal mathematical validity, but only one is physically relevant.

This image shows the parabola-like trajectory trail left by a rocket after launch. Many objects have left bizarre and unusual trails as they’ve zipped through our atmosphere, but none, at least so far, have indicated anything that goes beyond either conventional human technology or naturally occurring objects.

That’s not a deficiency in mathematics; that’s a feature of physics, and of science in general. Mathematics tells you the set of possible outcomes. But the scientific fact that we live in a physical reality — and in that reality, wherever and whenever we make a measurement, we observe only one outcome — teaches us that there are additional constraints beyond what mere mathematics provides. Mathematics tells you what outcomes are possible; physics (and science in general) is what you use to pick out which outcome is (or was, or will be) relevant for the specific problem you’re trying to address.

In biology, we can know the genetic makeup of two parent organisms, and can predict the probability with which their offspring will inherent a certain combination of genes. But if these two organisms combine their genetic material to actually make an offspring organism, only one set of combinations will be realized. Furthermore, the only way to determine which genes actually were inherited by the child of the two parents would be to make the critical observations and measurements: you have to gather the data and determine the outcome. Despite the myriad of mathematical possibilities, only one outcome actually occurs.

An Irish immigrant (center) waiting next to an Italian immigrant and her children at Ellis Island, circa 1920. The woman’s children each possess 50% of her DNA, but specifically which 50% is present in each child’s genetic makeup varies not only from child-to-child, but must be observed and measured, explicitly, to correctly determine which of all the possible outcomes actually occurred.

The more complicated your system, the more difficult it becomes to predict the outcome. For a room filled with large numbers of molecules, asking “What fate will befall any one of these molecules?” becomes a practically impossible task, as the number of possible outcomes after only a small amount of time passes becomes greater than the number of atoms in the entire Universe.

Some systems are inherently chaotic, where minuscule, practically immeasurable differences in the initial conditions of a system lead to vastly different potential outcomes.

Other systems are inherently indeterminate until they’re measured, which is one of the most counterintuitive aspects of quantum mechanics. Sometimes, the act of performing a measurement — to literally determine the quantum state of your system — winds up changing the state of the system itself.

In all of these cases, mathematics offers a set of possible outcomes whose probabilities can be determined and calculated in advance, but only by performing the critical measurement can you actually determine which one outcome has actually occurred.

Trajectories of a particle in a box (also called an infinite square well) in classical mechanics (A) and quantum mechanics (B-F). In (A), the particle moves at constant velocity, bouncing back and forth. In (B-F), wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. These stationary (B, C, D) and non-stationary (E, F) states only yield probabilities for the particle, rather than definitive answers for where it will be at a particular time.

This takes us all the way back to the initial question: what is the square root of 4?

Chances are, you read that question, and the number “2” immediately popped into your head. But that’s not the only possible answer; it could have been “-2” just as easily. After all, (-2)² equals 4 just as surely as (2)² equals 4; they’re both admissible solutions.

If I had gone further and asked, “What is the fourth root (the square root of the square root) of 16?” you could have then gone and given me four possible solutions. Each of these following numbers,

• 2,
• -2,
• 2i (where i is the square root of -1),
• and -2i,

when raised to the fourth power, will yield the number 16 as the mathematical answer.

This graph shows the function y = √x. Note that there are two possible solutions on the y-axis for every value of x. Two of those solutions correspond to x = 4: y = 2 and y = -2. Both solutions are, mathematically, equally valid. But there’s only one physical Universe that we inhabit, and each physical problem must be considered individually to determine which of these solutions is physically relevant.

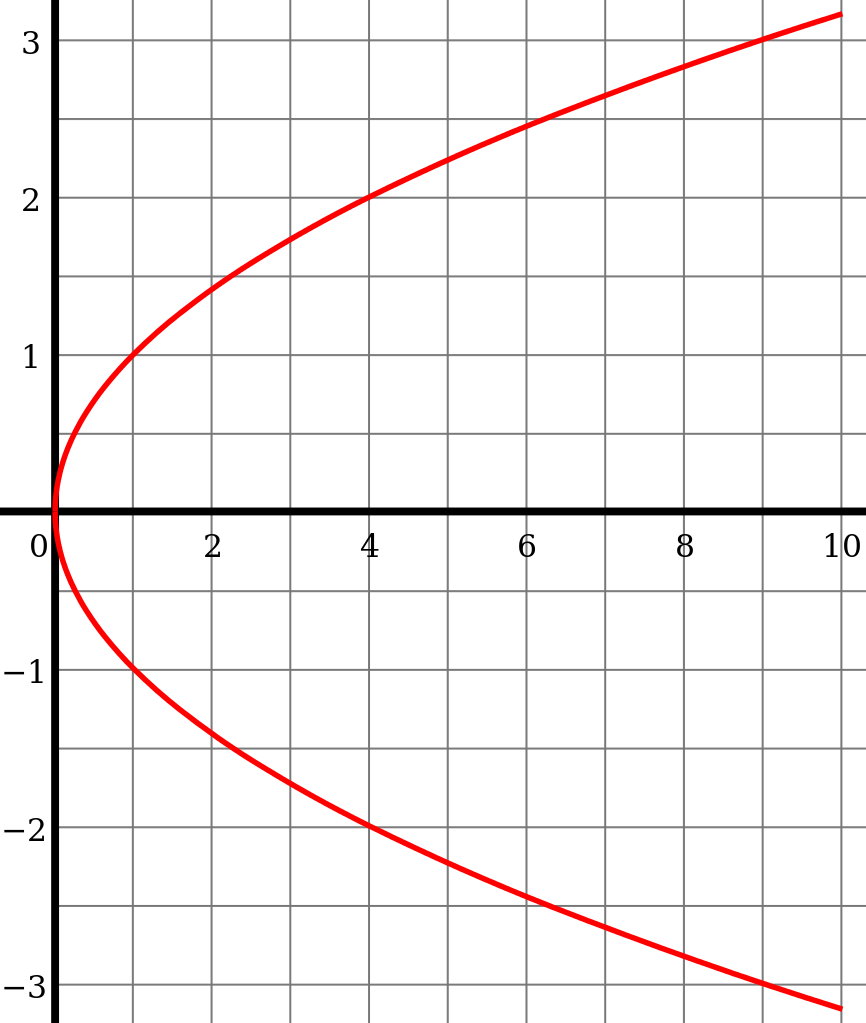
But in the context of a physical problem, there will only be one of these many possible solutions that actually reflects the reality we inhabit. The only way to determine which one is correct is either to go out and measure reality and pick out the physically relevant solution, or to know enough about your system and apply the relevant physical conditions so that you’re not simply calculating the mathematical possibilities, but that you’re capable of choosing the physically relevant solution and rejecting the non-physical ones.

Sometimes, that means we have multiple admissible solutions at once that are all plausible for explaining an observed phenomenon. It will only be through the obtaining of more, superior data that rules out certain possibilities while remaining consistent with others that enables us to determine which of the possible solutions actually remain viable. This approach, inherent to the process of doing science, helps us make successively better and better approximations to our inhabited reality, allowing us to tease out “what is true” about our Universe amidst the possibilities of “what could have been true” in the absence of that critical data.

NASA’s Curiosity Mars Rover detected fluctuations in the methane concentration of Mars’s atmosphere seasonally and at specific locations on the surface. This can be explained via either geochemical or biological processes; the evidence is not sufficient to decide at present. However, future missions, such as Mars Sample Return, may enable us to determine whether fossilized, dormant, or active life exists on Mars. Right now, we can only narrow down the physical possibilities; more information is required to determine which pathway accurately reflects our physical reality.

The biggest difference between physics and mathematics is simply that mathematics is a framework that, when applied wisely, can accurately describe certain properties about a physical system in a self-consistent fashion. However, mathematics is limited in what it can achieve: it can only give you a set of possible outcomes — sometimes weighted by probability and sometimes not weighted at all — for what could occur or could have occurred in reality.

Physics is much more than mathematics, however, as no matter when we look at the Universe or how we look at it, there will be only one observed outcome that has actually occurred. Mathematics shows us the full set of all possible outcomes, but it’s the application of physical constraints that allows us to actually determine what is true, real, or what actual outcomes have occurred in our reality.

If you can remember that the square root of 4 isn’t always 2, but is sometimes -2 instead, you can remember the difference between physics and mathematics. The latter can tell you all the possible outcomes that could occur, but what elevates something to the realm of science, rather than pure mathematics, is its connection to our physical reality. The answer to the square root of 4 will always be either 2 or -2, and the other solution will be rejected by a means that mathematics alone can never fully determine: on physical grounds, alone.