What is a black hole’s actual size?

Out there in the Universe, size definitely matters. An evolved red giant star, our Sun, and a white dwarf can all have the same mass, but the size difference between these three classes of objects is tremendous. While there might be some quantum effects that play a role for objects that are very small — in their energy, position, lifetime, etc. — there are some properties that remain the same regardless of any uncertainties. Objects that are stable, both microscopically and macroscopically, are described by measurable properties such as mass, volume, electric charge, and spin/angular momentum.

But “size” is a bit of a tricky one, particularly if your object is extremely small. The most extreme objects in terms of density are black holes, but for them, size isn’t necessarily a well-defined property. After all, if all the mass and energy that goes into making a black hole inevitably collapses to a central singularity, then what does the concept of “size” even mean? As it turns out, there’s actually more than one definition for a black hole’s size, and they all have their uses. From the outside in, let’s take a look at what a black hole’s size can tell us.

Instead of an empty, blank, three-dimensional grid, putting a mass down causes what would have been ‘straight’ lines to instead become curved by a specific amount. In general relativity, we treat space and time as continuous, but all forms of energy, including but not limited to mass, contribute to spacetime curvature. In addition, the distances between unbound objects evolve with time, owing to the expansion of the universe.

The first thing you have to know about a black hole is this: in terms of its gravitational effects, especially at large distances away from it, a black hole is no different from any other mass. If we were to somehow replace our Sun with an equal-mass, equal-angular momentum object that was:

• a swelling subgiant star,
• a large red giant that was the size of Venus’s orbit,
• a degenerate white dwarf,
• an ultra-compressed neutron star,
• or a black hole,

the gravitational effects we feel here on Earth would be absolutely unchanged.

Unless you’re a professional astrophysicist, this might surprise you! After all, we’re taught that black holes have an irresistible gravitational pull, and that they suck any matter that comes too close to their vicinity irrevocably into them. But the truth is that black holes don’t “suck” matter in anymore than any other mass. In fact, the only major difference between a black hole and any of these other objects is density: a black hole can have the same mass and angular momentum as any other object, but its small physical size means you can get closer to it, and that’s where these exotic gravitational effects arise.

An illustration of heavily curved spacetime, outside the event horizon of a black hole. As you get closer and closer to the mass’s location, space becomes more severely curved, eventually leading to a location from within which even light cannot escape: the event horizon.

Most of us know about a black hole’s event horizon, which represents the boundary between where an object can theoretically escape from its gravitational pull and where any object will inexorably be drawn into the central singularity, regardless of what it does. If your black hole consists of mass alone — no charge, no angular momentum, and no other “exotic” components inherent to it — the size of the event horizon is given by what’s known as the Schwarzschild radius: the radius at which the escape velocity equals the speed of light.

In reality, however, most (if not all) black holes that physically exist do have some sort of angular momentum inherent to them: evidence that they’re spinning about some rotational axis. When a black hole rotates, it no longer has just one meaningful surface that’s a boundary between what can escape and what can’t; instead, there are a number of important boundaries that arise, and many of them can make a claim to being the size of a black hole, depending on what you’re trying to do. From the outside in, let’s go through them.

An animation of the orbit of a single test particle just outside of the innermost stable orbit for a Kerr (rotating) black hole. Note that the particle has a differing radial extent from the black hole’s center dependent on the orientation: whether you’re aligned or perpendicular to the spin axis of the black hole. Note also that the particle doesn’t remain in a single plane, but rather fills the volume of a torus as it orbits the black hole.

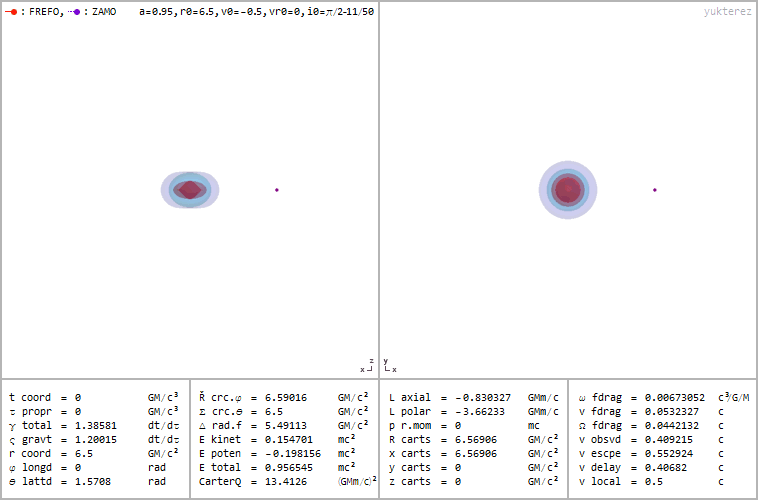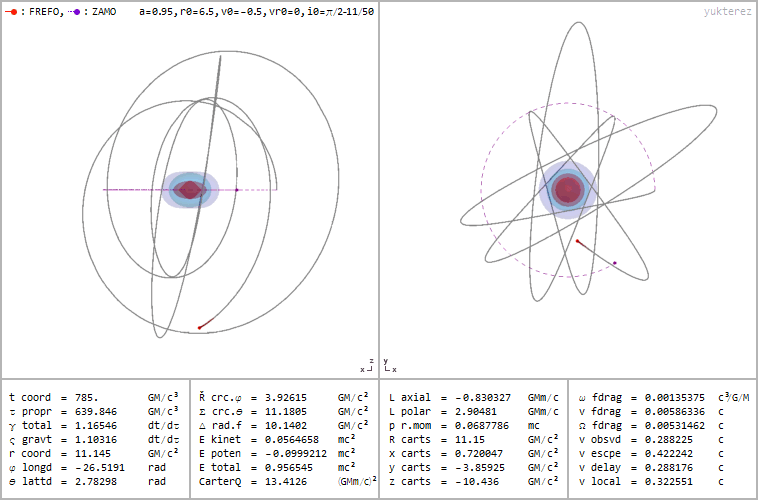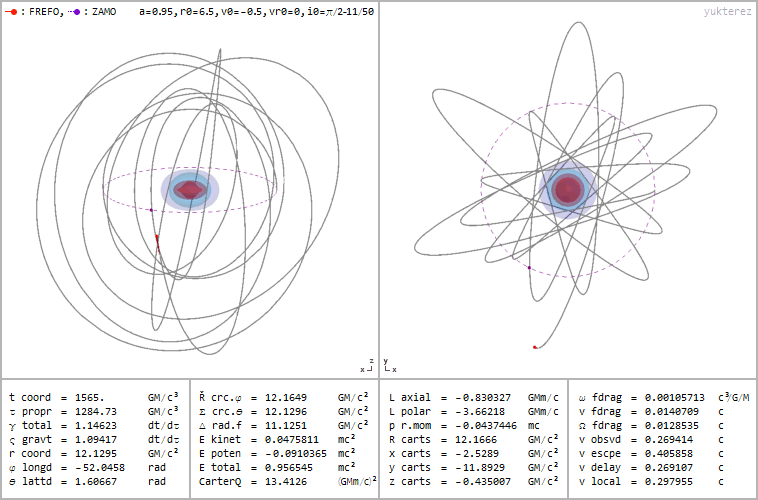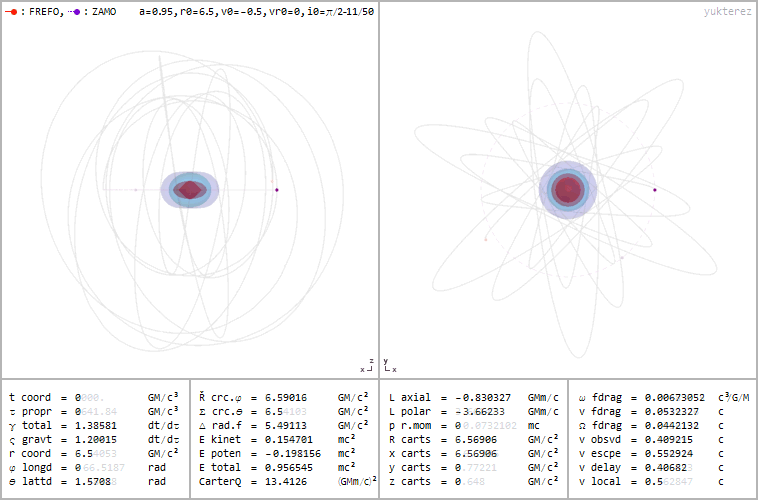
1.) Can I make a stable, circular orbit? This is the dream of anything that wants to spend its time gravitationally orbiting another body: to do it without constantly needing to add energy or thrust to keep you in orbit. Just as a satellite that orbits Earth too closely will be dragged back to our planet due to the frictional force of our tenuous outer atmosphere, an object that orbits a black hole, interior to a certain distance, will spiral into the black hole, cross the event horizon, and be drawn into the central singularity. That distance, where you can have a stable orbit, is known as ISCO: for innermost stable circular orbit.

This is significantly farther out than the event horizon itself: three times as distant as the Schwarzschild radius is, which applies to a non-rotating black hole. If your black hole is rotating, you have to go farther out: up to 4.5 times as distant as the Schwarzschild radius if you move retrograde (in the opposite direction) relative to the black hole’s spin for the maximum rotation rate allowed. On the other hand, though, prograde motion is easier, with your radius allowed to decrease slightly as the spin approaches its maximum. Still, this boundary is much larger, size-wise, than the black hole’s event horizon itself, and although you can remain confined to within a particular volume of space, you won’t simply remain in a stable, circular orbit.

On April 11, 2017, the Event Horizon Telescope team not only released their first image of a black hole, but modeled what they expected to see for a polarization signature. When they reconstructed the image of the first observed black hole with polarization included years later (left), it agreed with the model (right) exquisitely. This demonstrated that the physics of the matter surrounding these supermassive, rotating, plasma-rich black holes is pretty well understood. Note that the “shadow” of the black hole is larger than the size of the event horizon.

2.) What will I see when I look at it? This is a little bit paradoxical, because of the unprecedented success of the Event Horizon Telescope. When we created the first images of a black hole directly, we didn’t quite image the event horizon. Instead, what we imaged were the effects of photons in the vicinity of the black hole as they get bent by the intense curvature of space. Those photons then go off in many different directions, where we observe the ones that travel in a straight line to our eyes. We can see that photon flux and pinpoint where they are, and see that they make a diffuse, extended, ring-like shape, with only darkness on the inside.

But that ring isn’t the size of the event horizon; rather, due to some of the more intricate effects of General Relativity, it’s about 250% as large: slightly smaller than ISCO, but significantly larger than the Schwarzschild radius. These photons aren’t on stable orbits, but rather hyperbolic ones, where they escape the black hole’s gravitational pull. However, what arrives at our eyes isn’t representative of the physical size of the event horizon, but a diameter that’s 2.5 times as large as an event horizon’s actual diameter: the black hole’s “shadow” is larger than the black hole itself.

The exact solution for a black hole with both mass and angular momentum was found by Roy Kerr in 1963, and revealed, instead of a single event horizon with a point-like singularity, an inner and outer event horizon, as well as an inner and outer ergosphere, plus a ring-like singularity of substantial radius. An external observer cannot see anything beyond the outer event horizon, and if you replace the ring singularity with a non-singular object, the spacetime outside the horizon is unaffected.

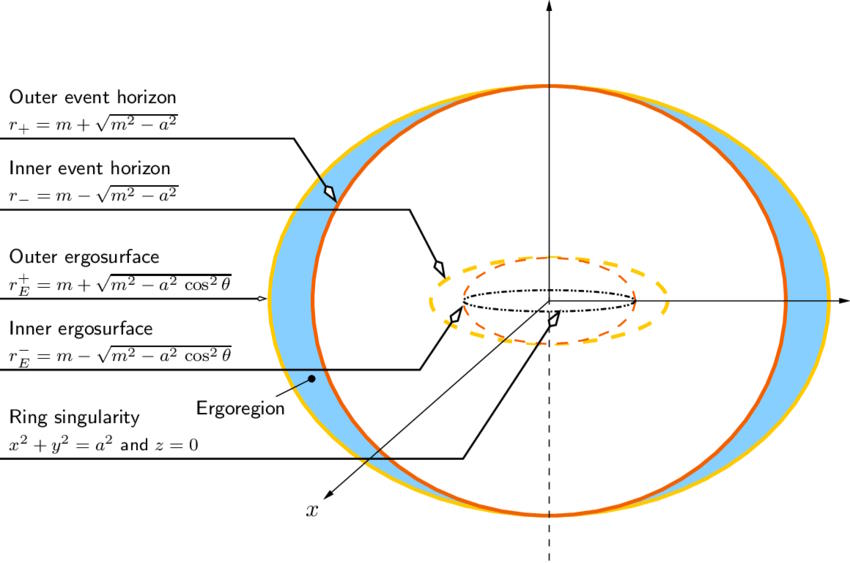
3.) Is there anything else interesting outside of the event horizon? Yes! There’s a location outside — 1.5 times the Schwarzschild radius for a non-rotating black hole and escalating up to twice the Schwarzschild radius for a maximally rotating one — known as the photon sphere: where a photon would remain in orbit around the black hole. But this isn’t for an indefinite period of time; a photon orbit is unstable, and will fall into the black hole. This doesn’t violate ISCO, because the “S” stands for stable; this is an unstable orbit.

But if your black hole is rotating, something else interesting comes along for the ride: what’s known as the outer ergosphere. Because of the black hole’s rotation, the space outside of it gets dragged as well. Sure, space always gets dragged by a rotating mass, but the ergosphere is special because it drags space at speeds equaling the speed of light.

In the outer ergosphere, particles that enter that region are forced to orbit faster, thereby gaining energy. If they gain enough energy, they can even escape the black hole entirely, getting kicked out and causing the black hole to pay a cost: losing energy. Typically, this comes from the spin energy, not the mass energy, and it’s one of the known ways to extract energy from a black hole. It’s known as the Penrose process, and is thought to be responsible for some of the highest-energy particles found in the Universe.

Shadow (black), horizons and ergospheres (white) of a rotating black hole. The quantity of a, shown varying in the image, has to do with the relationship of angular momentum of the black hole to its mass. Because actual matter must collapse to form this black hole, and because the conditions that necessarily lead to a singularity are not met under this scenario, the existence of a singularity is not guaranteed.

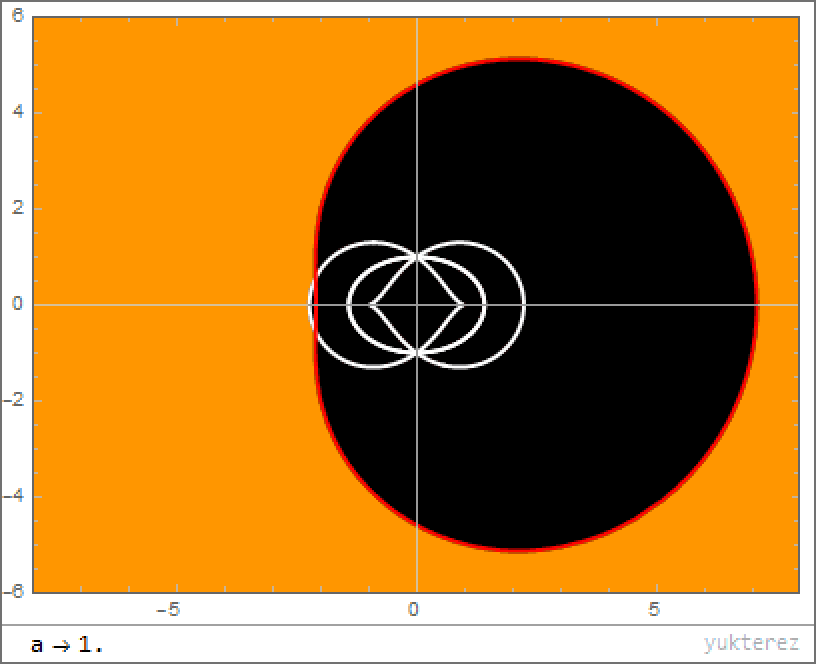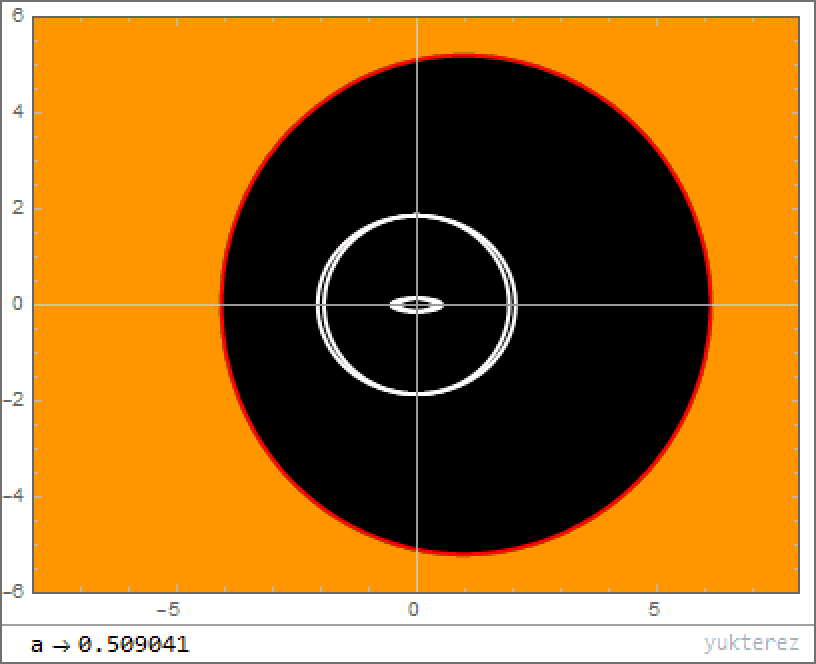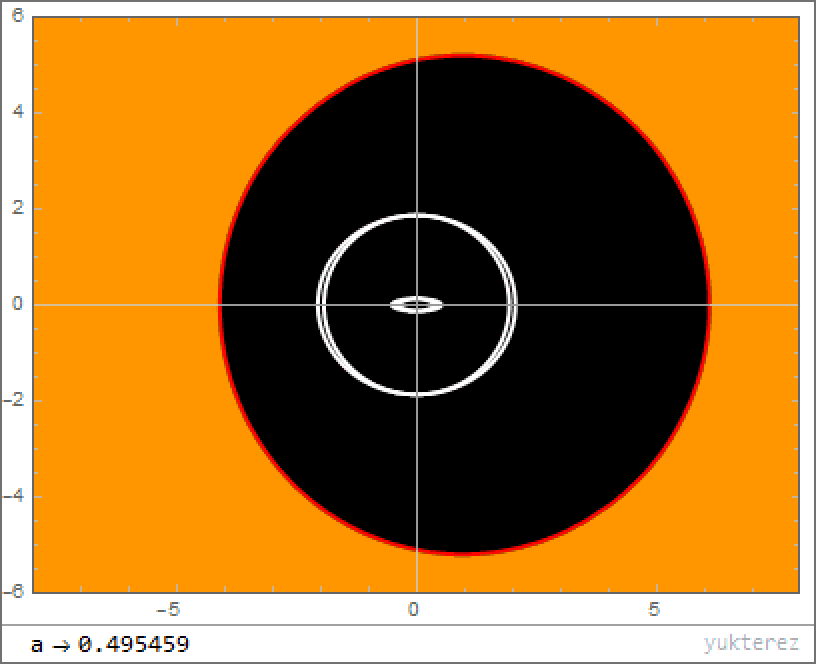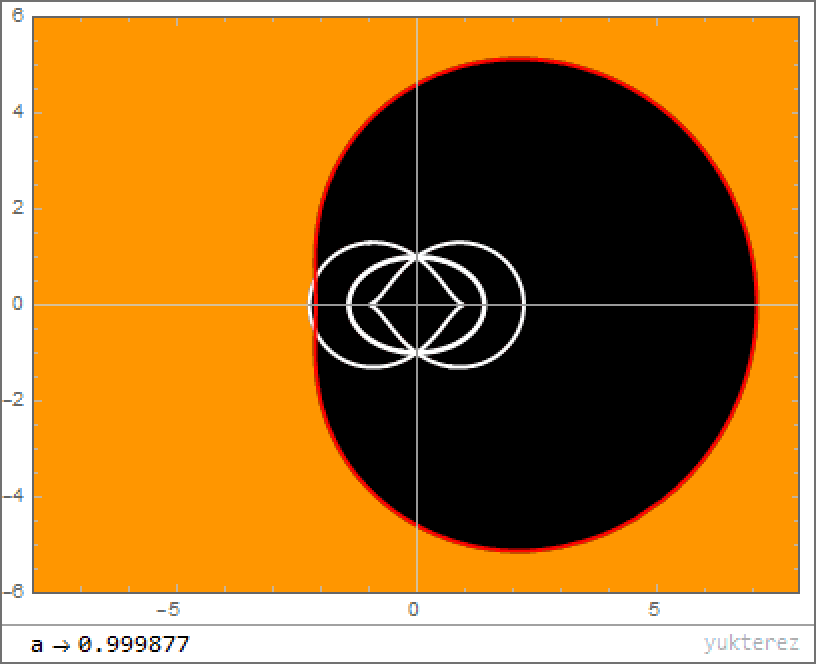
4.) What about the event horizon? As we’ve already stated, realistic black holes aren’t non-rotating; they spin with a significant amount of angular momentum. This rotation has a fascinating mathematical effect: instead of leading to one event horizon, you get two solutions, corresponding to an “outer” and “inner” event horizon. Although physicists argue over what these two solutions mean, the general consensus seems to be that the outer horizon definitely physically exists, while the inner horizon may not.

The outer horizon functions like the standard event horizon in the non-rotating case, but the rotation pushes it farther away: significantly further along the black hole’s “equator” than at the “poles.” The faster your black hole spins, the greater the distortion, up to a theoretical maximum rate. However, as we discussed earlier, black holes that spin too quickly will shed that spin energy from the Penrose process, spinning down toward a slower, more long-term stable state, further decreasing the event horizon’s size.

Both inside and outside the event horizon of a Schwarzschild black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, the gravitational acceleration decreases the farther away you position yourself.

5.) But what about inside the black hole’s outer event horizon? Now, here’s where things get really interesting for a detail-oriented physicist. If our black hole weren’t rotating, once you crossed the event horizon, you would inexorably fall toward the central singularity, with no other alternative. You wouldn’t, however, be able to see everything else coming from every other direction in space; rather, the parts of the interior of the black hole that are causally connected make a particular mathematical shape: a heart-shaped curve known as a cardiod.

The singularity that you’d eventually reach would be point-like, and would have an infinite density (and an infinitesimally small volume) as a result. Although we don’t know what happens at the singularity — we’d need a quantum theory of gravity to know for certain — it’s very clear that our known laws of physics break down, yielding only nonsense answers.

However, if you allow your black hole to rotate, meaning it has not only mass inherent to it but also angular momentum, everything changes.

In the vicinity of a black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, though, other forces (like electromagnetism) can frequently overcome the pull of gravity, causing even infalling matter to escape.

6.) What’s a realistic black hole’s singularity like? First off, if you add rotation into the mix, your singularity is no longer a zero-dimensional point, but rather it gets spread out into a one-dimensional structure: a ring. When you fall into a rotating black hole, you do head toward the singularity, but the rotating nature of spacetime sort of smears you out into a vortex-like shape; it’s like “spaghettification” but with a swirl to it. Your trajectory will hurl each individual quantum in your body into a different point, distributed along this linear ring.

But there’s a fun caveat: there are some theoretical indications that when you cross over past the outer event horizon and head toward the inner event horizon, it’s equivalent to birthing a new Universe inside of that black hole. Many relativists argue over what a number of properties that we’ve derived mean.

• Do you wind up with a state similar to the one we expect occurred during cosmic inflation?
• Does it appear that the boundary you encounter can be mapped onto a boundary that leads to another hot Big Bang?
• Is it akin to a wormhole, where you “exit” the space you’ve been occupying and re-emerge elsewhere (and elsewhen) in some new space?

The possibilities are fascinating, and indicate that you might not ever hit that singularity if your black hole rotates, after all.

From outside a black hole, all the infalling matter will emit light and is always visible, while nothing from behind the event horizon can get out. But if you were the one who fell into a black hole, your energy could conceivably re-emerge as part of a hot Big Bang in a newborn Universe.

And yet, for as careful as physicists are when we talk about all these issues and all the different ways there are to define “size” for a black hole, we tend to be lazy when we speak colloquially. Typically, a black hole’s size, in the mouth of a physicist, means the Schwarzschild radius of the black hole, regardless of spin, and neglecting any of the other effects of spatial curvature, the apparent size of a shadow, or the behavior of particles. Just treat the black hole as a point-like mass, calculate at what radius its escape velocity equals the speed of light, and there’s your size. Even if you only use Newtonian gravity to figure it out, your results will be remarkably accurate.

Of course, there are many other physical scenarios we consider all of the time.

• What happens to the particles outside a black hole?
• Where can they stably orbit, versus where will they either get ejected or swallowed?
• What do we physically see when we look at a black hole?
• When a black hole rotates, what effects does the dragging of space have on the matter outside of the black hole?
• And, if you journey past the event horizon of a black hole, what would you go on to experience or encounter?

All of these questions have different answers, with different implications for the question of size. It’s important, when we talk about these issues, that we always use the definition of size that makes sense for the effect we’re exploring. Anything else can only lead to confusion.