Ask Ethan: What happens when a black hole’s singularity evaporates?

If even black holes won’t last forever, what will happen when the last one goes?

“My discovery that black holes emit radiation raised serious problems of consistency with the rest of physics. I have now resolved these problems, but the answer turned out to be not what I expected.” –Stephen Hawking

It’s hard to imagine, given the full diversity of forms that matter takes in this Universe, that for millions of years, there were only neutral atoms of hydrogen and helium gas. It’s perhaps equally hard to imagine that someday, quadrillions of years from now, all the stars will have gone dark. Only the remnants of our now-vibrant Universe will be left, including some of the most spectacular objects of all: black holes. But even they won’t last forever. David Weber wants to know how that happens for this week’s Ask Ethan, inquiring:

What happens when a black hole has lost enough energy due to hawking radiation that its energy density no longer supports a singularity with an event horizon? Put another way, what happens when a black hole ceases to be a black hole due to hawking radiation?

In order to answer this question, it’s important to understand what a black hole actually is.

Black holes generally form during the collapse of a massive star’s core, where the spent nuclear fuel ceases to fuse into heavier elements. As fusion slows and ceases, the core experiences a severe drop in radiation pressure, which was the only thing holding the star up against gravitational collapse. While the outer layers often experience a runaway fusion reaction, blowing the progenitor star apart in a supernova, the core first collapses into a single atomic nucleus — a neutron star — but if the mass is too great, the neutrons themselves compress and collapse to such a dense state that a black hole forms. (A black hole can also form if a neutron star accretes enough mass from a companion star, crossing the threshold necessary to become a black hole.)

From a gravitational point of view, all it takes to become a black hole is to gather enough mass in a small enough volume of space that light cannot escape from within a certain region. Every mass, including planet Earth, has an escape velocity: the speed you’d need to achieve to completely escape from the gravitational pull at a given distance (e.g., the distance from Earth’s center to its surface) from its center-of-mass. But if there’s enough mass so that the speed you’d need to achieve at a certain distance from the center of mass is the speed of light or greater, then nothing can escape from it, since nothing can exceed the speed of light.

That distance from the center of mass where the escape velocity equals the speed of light — let’s call it R — defines the size of the black hole’s event horizon. But the fact that there’s matter inside under these conditions has another consequence that’s less-well appreciated: this matter must collapse down to a singularity. You might think there could be a state of matter that’s stable and has a finite volume within the event horizon, but that’s not physically possible.

In order to exert an outward force, an interior particle would have to send a force-carrying particle away from the center-of-mass and closer to the event horizon. But that force-carrying particle is also limited by the speed of light, and no matter where you are inside the event horizon, all light-like curves wind up at the center. The situation is even worse for slower, massive particles. Once you form a black hole with an event horizon, all the matter inside gets crunched into a singularity.

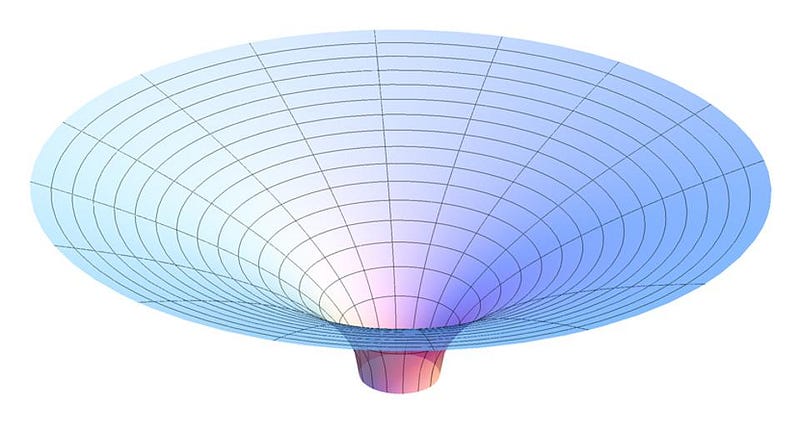
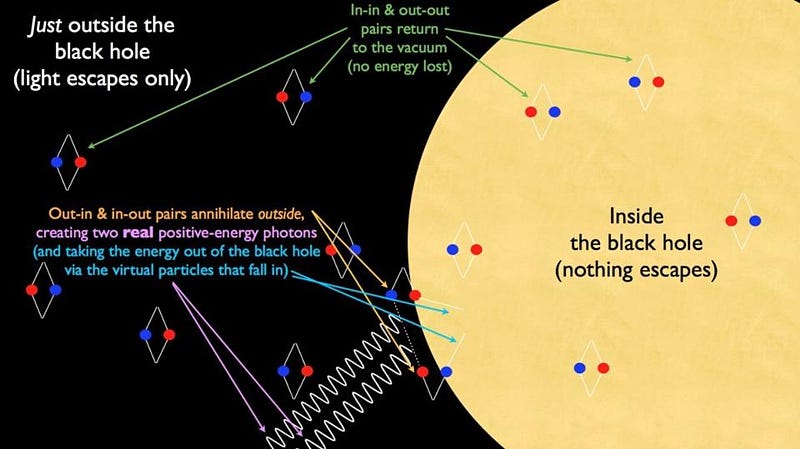
And since nothing can escape, you might think a black hole would remain a black hole forever. If it weren’t for quantum physics, this would be exactly what happens. But in quantum physics, there’s a non-zero amount of energy inherent to space itself: the quantum vacuum. In curved space, the quantum vacuum takes on slightly different properties than in flat space, and there are no regions where the curvature is greater than near the singularity of a black hole. Combining these two laws of nature — quantum physics and the General Relativistic spacetime around a black hole — gives us the phenomenon of Hawking radiation.

Performing the quantum field theory calculation in curved space yields a surprising solution: that thermal, blackbody radiation is emitted in the space surrounding a black hole’s event horizon. And the smaller the event horizon is, the greater the curvature of space near the event horizon is, and thus the greater the rate of Hawking radiation. If our Sun were a black hole, the temperature of the Hawking radiation would be about 62 nanokelvin; if you took the black hole at the center of our galaxy, 4,000,000 times as massive, the temperature would be about 15 femtokelvin, or just 0.000025% the temperature of the less massive one.

This means the smallest black holes decay the fastest, and the largest ones live the longest. Doing the math, a solar mass black hole would live for about 10⁶⁷ years before evaporating, but the black hole at the center of our galaxy would live for 10²⁰ times as long before decaying. The crazy thing about it all is that right up until the final fraction-of-a-second, the black hole still has an event horizon. Once you form a singularity, you remain a singularity — and you retain an event horizon — right up until the moment your mass goes to zero.

That final second of a black hole’s life, however, will result in a very specific and very large release of energy. When the mass drops down to 228 metric tonnes, that’s the signal that exactly one second remains. The event horizon size at the time will be 340 yoctometers, or 3.4 × 10^-22 meters: the size of one wavelength of a photon with an energy greater than any particle the LHC has ever produced. But in that final second, a total of 2.05 × 10²² Joules of energy, the equivalent of five million megatons of TNT, will be released. It’s as though a million nuclear fusion bombs went off all at once in a tiny region of space; that’s the final stage of black hole evaporation.

What’s left? Just outgoing radiation. Whereas previously, there was a singularity in space where mass, and possibly charge and angular momentum existed in an infinitesimally small volume, now there is none. Space has been restored to its previously non-singular state, after what must have seemed like an eternity: enough time for the Universe to have done all it’s done to date trillions upon trillions of times over. There will be no other stars or sources of light left when this occurs for the first time in our Universe; there will be no one to witness this spectacular explosion. But there’s no “threshold” where this occurs. Rather, the black hole needs to evaporate completely. When it does, to the best of our knowledge, there will be nothing left behind at all but outgoing radiation.

In other words, if you were to watch the last black hole in our Universe evaporate, you would see an empty void of space, that displayed no light or signs of activity for perhaps 10¹⁰⁰ years or more. All of a sudden, a tremendous outrush of radiation of a very particular spectrum and magnitude would appear, leaving a single point in space at 300,000 km/s. For the last time in our observable Universe, an event would have occurred to bathe the Universe in radiation. The last black hole evaporation of all would, in a poetic way, be the final time that the Universe would ever say, “Let there be light!”

Send in your Ask Ethan questions to startswithabang at gmail dot com!