Why 21 cm is the magic length for the Universe

In our Universe, quantum transitions are the governing rule behind every nuclear, atomic, and molecular phenomenon. Unlike the planets in our Solar System, which could stably orbit the Sun at any distance if they possessed the right speed, the protons, neutrons, and electrons that make up all the conventional matter we know of can only bind together in a specific set of configurations. These possibilities, although numerous, are finite in number, as the quantum rules that govern electromagnetism and the nuclear forces restrict how atomic nuclei and the electrons that orbit them can arrange themselves.

In all the Universe, the most common atom of all is hydrogen, with just one proton and one electron. Wherever new stars form, hydrogen atoms become ionized, becoming neutral again if those free electrons can find their way back to a free proton. Although the electrons will typically cascade down the allowed energy levels into the ground state, that normally produces only a specific set of infrared, visible, and ultraviolet light. But more importantly, a special transition occurs in hydrogen that produces light of about the size of your hand: 21 centimeters (about 8¼”) in wavelength. That’s a magic length, and it just might someday unlock the darkest secrets hiding out in the recesses of the Universe.

Backlit by the cosmic microwave background, a cloud of neutral gas can imprint a signal on that radiation at a specific wavelength and redshift. If we can measure this light with great enough sensitivity, we can actually hope to someday map out the locations and densities of gas clouds in the Universe thanks to the science of 21 cm astronomy. A dip in brightness temperature at redshifts of 15-20, observed in 2018, may be due to exactly the effect of 21-cm emission, although better instrumentation and better observational examples will be required to confirm such a claimed detection.

When it comes to the light in the Universe, wavelength is the one property that you can count on to reveal how that light was created. Even though light comes to us in the form of photons — individual quanta that, collectively, make up the phenomenon we know as light — there are two very different classes of quantum process that create the light that surrounds us: continuous ones and discrete ones.

A continuous process is something like the light emitted by the photosphere of the Sun. It’s a dark object that’s been heated up to a certain temperature, and it radiates light of all different, continuous wavelengths as dictated by that temperature: what physicists know as blackbody radiation.

A discrete process, however, doesn’t emit light of a continuous set of wavelengths, but rather only at extremely specific wavelengths. A good example of that is the light absorbed by the neutral atoms present within the extreme outer layers of the Sun. As the blackbody radiation strikes those neutral atoms, a few of those photons will have just the right wavelengths to be absorbed by the electrons within the neutral atoms they encounter. When we break sunlight up into its individual wavelengths, the various absorption lines present against the backdrop of continuous, blackbody radiation reveal both of these processes to us.

The visible light spectrum of the Sun, which helps us understand not only its temperature and ionization, but the abundances of the elements present. The long, thick lines are hydrogen and helium, but every other line is from a heavy element that must have been created in a previous-generation star, rather than the hot Big Bang.

Each individual atom has its properties primarily defined by its nucleus, made up of protons (which determine its charge) and neutrons (which, combined with protons, determine its mass). Atoms also have electrons, which orbit the nucleus and occupy a specific set of energy levels. In isolation, each atom will come to exist in the ground state: where the electrons cascade down until they occupy the lowest allowable energy levels, limited only by the quantum rules that determine the various properties that electrons are and aren’t allowed to possess.

Electrons can occupy the ground state — the 1s orbital — of an atom until it’s full, which can hold two electrons. The next energy level up consists of spherical (the 2s) and perpendicular (the 2p) orbitals, which can hold two and six electrons, respectively, for a total of eight. The third energy level can hold 18 electrons: 3s (with two), 3p (with six), and 3d (with ten), and the pattern continues on upward. In general, the “upward” transitions rely on the absorption of a photon of particular wavelengths, while the “downward” transitions result in the emission of photons of the exact same wavelengths.

Electron transitions in the hydrogen atom, along with the wavelengths of the resultant photons, showcase the effect of binding energy and the relationship between the electron and the proton in quantum physics. The Bohr model of the atom provides the coarse (or rough, or gross) structure of these energy levels. Hydrogen’s brightest atomic transition is Lyman-alpha (n=2 to n=1), but its second brightest is visible: Balmer-alpha (n=3 to n=2), which emits visible (red) light at a wavelength of 656 nanometers. The energy lost by an electron cascading down the energy levels gets emitted in the form of photons.

That’s the basic structure of an atom, sometimes referred to as “coarse structure.” When you transition from the third energy level to the second energy level in a hydrogen atom, for example, you produce a photon that’s red in color, with a wavelength of precisely 656.3 nanometers: right in the visible light range of human eyes.

But there are very, very slight differences between the exact, precise wavelength of a photon that gets emitted if you transition from:

• the third energy level down to either the 2s or the 2p orbital,
• an energy level where the spin angular momentum and the orbital angular momentum are aligned to one where they’re anti-aligned,
• or one where the nuclear spin and the electron spin are aligned versus anti-aligned.

There are rules as to what’s allowed versus what’s forbidden in quantum mechanics as well, such as the fact that you can transition an electron from a d-orbital to either an s-orbital or a p-orbital, and from an s-orbital to a p-orbital, but not from an s-orbital to another s-orbital.

The slight differences in energy between different types of orbital within the same energy level is known as an atom’s fine-structure, arising from the interaction between the spin of each particle within an atom and the orbital angular momentum of the electrons around the nucleus. It causes a shift in wavelength of less than 0.1%: small but measurable and significant.

The atomic transition from the 6S orbital in a cesium-133 atom, Delta_f1, is the transition that defines the meter, second, and the speed of light. Slight changes in the observed frequency of this light will occur based on motion and the properties of spatial curvature between any two locations. Spin-orbit interactions, as well as various quantum rules and the application of an external magnetic field, can cause additional splitting at narrow intervals in these energy levels: examples of fine and hyperfine structure.

But in quantum mechanics, even “forbidden” transitions can sometimes occur, owing to the phenomenon of quantum tunneling. Sure, you might not be able to transition from an s-orbital to another s-orbital directly, but if you can:

• transition from an s-orbital to a p-orbital and then back to an s-orbital,
• transition from an s-orbital to a d-orbital and then back to an s-orbital,
• or, more generally, transition from an s-orbital to any other allowable state and then back to an s-orbital,

then that transition can occur. The only thing weird about quantum tunneling is that you don’t have to have a “real” transition occur with enough energy to make it happen to the intermediate state; it can happen virtually, so that you only see the final state emerge from the initial state: something that would be forbidden without the invocation of quantum tunneling.

This allows us to go beyond mere “fine structure” and onto hyperfine structure, where the spin of the atomic nucleus and one of the electrons that orbit it begin in an “aligned” state, where the spins are both in the same direction even though the electron is in the lowest-energy, ground (1s) state, to an anti-aligned state, where the spins are reversed.

Whenever a neutral hydrogen atom forms, the electron within it will spontaneously de-excite until it’s in the lowest (1s) state of the atom. With a 50/50 chance of having those spins of the electron and proton aligned, half of those atoms will be able to quantum tunnel into the anti-aligned state, emitting radiation of 21 centimeters (1420 MHz) in the process. This should allow us to probe clumps of neutral hydrogen even farther back than the existence of the first stars.

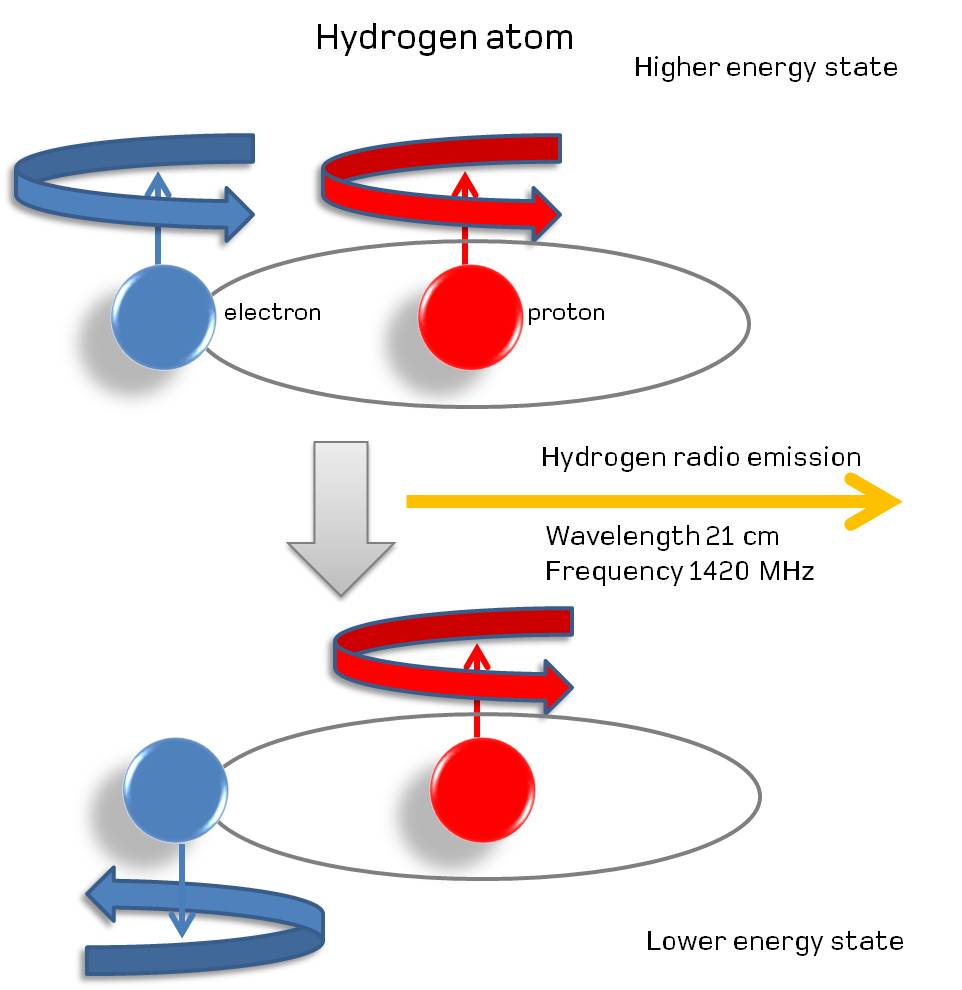
The most famous of these transitions occurs in the simplest type of atom of all: hydrogen. With just one proton and one electron, every time you form a neutral hydrogen atom and the electron cascades down to the ground (lowest-energy) state, there’s a 50% chance that the spins of the central proton and the electron will be aligned, with a 50% chance that the spins will be anti-aligned.

If the spins are anti-aligned, that’s truly the lowest-energy state; there’s nowhere to go via transition that will result in the emission of energy at all. But if the spins are aligned, it becomes possible to quantum tunnel to the anti-aligned state: even though the direct transition process is forbidden, tunneling allows you to go straight from the starting point to the ending point, emitting a photon in the process.

This transition, because of its “forbidden” nature, takes an extremely long time to occur: approximately 10 million years for the average atom. However, this long lifetime of the slightly excited, aligned case for a hydrogen atom has an upside to it: the photon that gets emitted, at 21 centimeters in wavelength and with a frequency of 1420 megahertz, is intrinsically, extremely narrow. In fact, it’s the narrowest, most precise transition line known in all of atomic and nuclear physics!

This map of the Milky Way, in red, maps out the neutral hydrogen in 21 centimeter emissions. This map is not uniform, but rather tracks recent ionization and atom formation, as the half-life of spin-aligned atoms to flip is only around ~10 million years: a long time in the lab, but a short time compared to the ~13+ billion year history of our galaxy.

If you were to go all the way back to the early stages of the hot Big Bang, before any stars had formed, you’d discover that a whopping 92% of the atoms in the Universe were exactly this species of hydrogen: with one proton and one electron in them. As soon as neutral atoms stably form — just a few hundred thousand years after the Big Bang — these neutral hydrogen atoms form with a 50/50 chance of having aligned versus anti-aligned spins. The ones that form anti-aligned will remain so; the ones that form with their spins aligned will undergo this spin-flip transition, emitting radiation of 21 centimeters in wavelength.

Although it’s never yet been done, this gives us a tremendously provocative way to measure the early Universe: by finding a cloud of hydrogen-rich gas, even one that’s never formed stars, we could look for this spin-flip signal — accounting for the expansion of the Universe and the corresponding redshift of the light — to measure the atoms in the Universe from the earliest times ever seen. The only “broadening” to the line we’d expect to see would come from thermal and kinetic effects: from the non-zero temperature and the gravitationally-induced motion of the atoms that emit those 21 centimeter signals.

If particles that emitted radiation were completely at rest and were at a temperature indistinguishable from absolute zero, the width of any emission lines would be determined solely by the speed of the transition. The 21 cm hydrogen line is incredibly, intrinsically narrow, but the kinetic motion of the material in galaxies, as well as the thermal energy because the gas is at a positive, non-zero temperature, both contribute to the observed width of these lines.

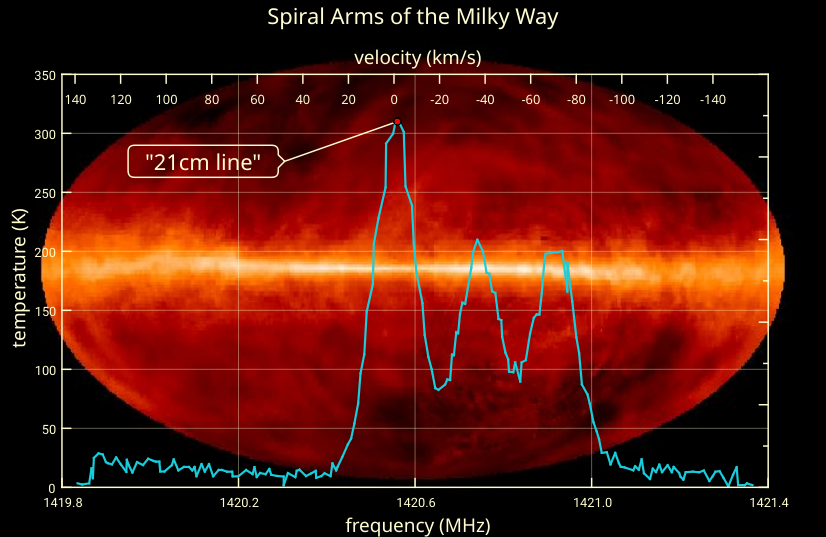
In addition to those primordial signals, 21 centimeter radiation arises as a consequence whenever new stars are produced. Every time that a star-forming event occurs, the more massive newborn stars produce large amounts of ultraviolet radiation: radiation that’s energetic enough to ionize hydrogen atoms. All of a sudden, space that was once filled with neutral hydrogen atoms is now filled with free protons and free electrons.

But those electrons are going to eventually be captured, once again, by those protons, and when there’s no longer enough ultraviolet radiation to ionize them over and over again, the electrons will once again sink down to the ground state, where they’ll have a 50/50 chance of being aligned or anti-aligned with the spin of the atomic nucleus.

Again, that same radiation — of 21 centimeters in wavelength — gets produced, and every time we measure that 21 centimeter wavelength localized in a specific region of space, even if it gets redshifted by the expansion of the Universe, what we’re seeing is evidence of recent star-formation. Wherever star-formation occurs, hydrogen gets ionized, and whenever those atoms become neutral and de-excite again, this specific-wavelength radiation persists for tens of millions of years.

When a hydrogen atom forms, it has equal probability of having the electron’s and proton’s spins be aligned and anti-aligned. If they’re anti-aligned, no further transitions will occur, but if they’re aligned, they can quantum tunnel into that lower energy state, emitting a photon of a very specific wavelength (21 cm) on very specific, and rather long, timescales. The precision of this transition has been measured to better than 1-part-in-a-trillion, and has not varied over the many decades it’s been known. It is the first light emitted in the Universe after the formation of neutral atoms: even before the formation of the first stars, but also thereafter: whenever new stars are formed, ultraviolet emission ionizes hydrogen atoms, creating this signature once again when those atoms spontaneously re-form.

If we had the capability of sensitively mapping this 21 centimeter emission in all directions and at all redshifts (i.e., distances) in space, we could literally uncover the star-formation history of the entire Universe, as well as the de-excitation of the hydrogen atoms first formed in the aftermath of the hot Big Bang. With sensitive enough observations, we could answer questions like:

• Are there stars present in dark voids in space below the threshold of what we can observe, waiting to be revealed by their de-exciting hydrogen atoms?
• In galaxies where no new star-formation is observed, is star-formation truly over, or are there low-levels of new stars being born, just waiting to be discovered from this telltale signature of hydrogen atoms?
• Are there any events that heat up and lead to hydrogen ionization prior to the formation of the first stars, and are there star-formation bursts that exist beyond the capabilities of even our most powerful infrared observatories to observe directly?

By measuring light of precisely the needed wavelength — 21.106114053 centimeters, plus whatever lengthening effects arise from the cosmic expansion of the Universe — we could reveal the answers to all of these questions and more. In fact, this is one of the main science goals of LOFAR: the low-frequency array, and it presents a strong science case for putting an upscaled version of this array on the radio-shielded far side of the Moon.

Constructing either a very large radio dish, perhaps in a lunar crater, or alternatively an array of radio telescopes, on the far side of the Moon, could enable unparalleled radio observations of the Universe, including in the all-important 21 centimeter range, both nearby and across cosmic time. The ability to map out where neutral hydrogen has newly formed within the past ~10-20 million years would advance our understanding of cosmic history like nothing else.

Of course, there’s another possibility that takes us far beyond astronomy when it comes to making use of this important length: creating and measuring enough spin-aligned hydrogen atoms in the lab to detect this spin-flip transition directly, in a controlled fashion. The transition takes about ~10 million years to “flip” on average, which means we’d need around a quadrillion (10¹⁵) prepared atoms, kept still and cooled to cryogenic temperatures, to measure not only the emission line, but the width of it. If there are phenomena that cause an intrinsic line-broadening, such as a primordial gravitational wave signal, such an experiment would, quite remarkably, be able to uncover its existence and magnitude.

In all the Universe, there are only a few known quantum transitions with the precision inherent to the hyperfine spin-flip transition of hydrogen, resulting in the emission of radiation that’s 21 centimeters in wavelength. If we want to identify ongoing and recent star-formation across the Universe, the first atomic signals even before the first stars were formed, or the relic strength of yet-undetected gravitational waves left over from cosmic inflation, it becomes clear that the 21 centimeter transition is the most important probe we have in all the cosmos. In many ways, it’s the “magic length” for uncovering some of nature’s greatest secrets.