Ask Ethan: Why is fusion in stars different than during the Big Bang?

- When the Universe began with the hot Big Bang, there were no atoms or even atomic nuclei; they had to form out of simpler building blocks, like pure protons and neutrons.
- Nuclear fusion reactions first occurred during the early stages of the hot Big Bang, and then didn’t happen again for tens-to-hundreds of millions of years: when the first stars formed.
- Despite the fact that fusion occurred at both the Big Bang and in stars, they’re extremely different from one another. Here’s why it matters for the Universe.
In all the Universe, there’s arguably no reaction more important than nuclear fusion. Without it, hydrogen would be the only element in the Universe. Without it, there would be no shining stars throughout the Universe. Without it, planets wouldn’t be possible, and there would be no instances of life in the entire cosmos. And yet, of the two places where nuclear fusion is known to copiously occur — during the first few minutes of the hot Big Bang and in the cores of stars — there’s more that’s different than similar between them.
Why is that the case? What happens in stars versus the Big Bang that makes the fusion process so different? That’s the question of John Fulton, who wants to know:
“[What is the] difference between thermonuclear fusion in the early Universe and in the cores of Sun-like stars? Why are the steps different? Early on, we have a deuteron interacting with a proton, but in a Sun-like star, we have two protons interacting. Why is the former more likely in the early Universe? Is there anything more than that?”
Nuclear fusion reactions are at play in both scenarios, true. But there are many fundamental differences not only in the processes that occur, but what the conditions for and outcomes of nuclear fusion are. Let’s break it all down.

At a fundamental level, nuclear fusion is simply the process of:
- bringing two or more protons, neutrons, or heavier nuclei made up of protons and neutrons together,
- under conditions that cause them to combine into a still-heavier nucleus,
- where a net amount of energy is released from the reaction.
The reason that energy can be released is because when protons and neutrons bind together, they’ll configure themselves in the most stable way possible. Although the positive charges on each proton will repel one another, there’s another force — the strong nuclear force — that’s mutually attractive and that affects every proton and neutron within a nucleus.
When you fuse light elements together into heavier ones, they can attain a more stable configuration if you add the proper ratios of protons to neutrons. In other words, when you have a nuclear fusion reaction, the mass of the final fusion product can be less than the mass of all the initial reactant particles. From Einstein’s most famous equation, E = mc2, that “missing mass” gets converted into pure energy. This not only enables the reaction to spontaneously occur under the proper conditions, but results in the emission of high-energy radiation from most fusion reactions.

The first time nuclear fusion occurred was in the early Universe, well before the formation of any stars, galaxies, planets, or other large-scale, macroscopic structure. Instead, we can go all the way back to a time where individual protons and neutrons were first forming: at the time that the early quark-gluon plasma finally cooled sufficiently and the density dropped to low enough values that such an event could occur.
Initially, the Universe was 50% protons and 50% neutrons, and even though both the temperatures and densities were high enough for fusion to occur, it didn’t.
Why not?
Because there were too many photons of too high an energy. Any time a proton and a neutron found each other, they’d immediately fuse together to form deuterium, which releases energy. Unfortunately, the early stages of the Big Bang aren’t just hot enough to allow nuclear fusion to occur, they’re also hot enough that a large fraction of the photons present are energetic enough to split apart any nucleus that’s made up of protons and neutrons back into their individual components.

Given that photons outnumber protons and neutrons by more than a billion-to-one, we have to wait for the Universe to cool in order for nuclear fusion to proceed. There are three ways, in theory, that nature could have taken that first step, from pure protons and neutrons, to creating heavier elements.
- The first step could have been a proton fusing with a neutron, producing a composite particle known as a deuteron (a proton and neutron bound together). A deuteron is stable, although a high-enough energy collision can destroy it.
- The first step could have been a proton fusing with a proton, producing a diproton (two protons bound together), which is unstable. However, there’s a tiny quantum mechanical chance that, rather than decaying back to two protons, it can quantum tunnel into a state where it produces a deuteron, along with a positron and an electron neutrino.
- Or the first step could have been a neutron fusing with a neutron, producing a dineutron (two neutrons bound together), which is also unstable. Dineutrons will decay into two neutrons, as first observed in 2012, although they may be able to quantum tunnel into a deuteron before decaying, with a small probability for that not-yet-observed process.
With so many neutrons present in the early Universe, it’s almost certainly the first step that dominates deuteron production in the immediate aftermath of the Big Bang, but none of that can happen until the Universe cools below a critical threshold, otherwise the produced deuterons get immediately blasted apart.
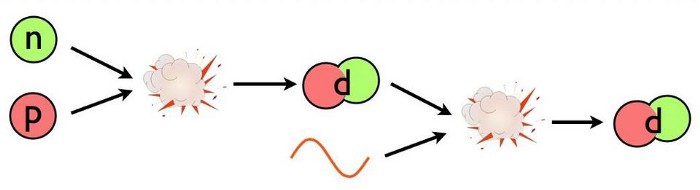
For nuclear fusion to produce stable atomic nuclei, there must be nothing around that will destroy these heavier isotopes faster than the Universe can make them. That requires the Universe to expand and cool for somewhere between three and four minutes: a relative eternity in the earliest moments of the hot Big Bang. Over that time interval, numerous changes occur.
- Protons and neutrons collide with electrons, positrons, and neutrinos and antineutrinos, interconverting to keep that 50/50 ratio, initially.
- As the Universe cools, it gets harder to make neutrons but easier to make protons.
- As it loses energy further, the neutrinos stop interacting.
- As the Universe cools even more, the excess electrons and positrons annihilate away, heating up the photons slightly and leaving only enough negatively charged electrons to balance the positively charged protons.
- And then the free neutrons begin to radioactively decay, with a half-life of about 10 minutes.
By the time that the photons have finally cooled enough that they won’t immediately blast any deuterium apart, protons and neutrons are no longer in a 50/50 ratio, but more like a 88/12 ratio. But this time, nuclear fusion can finally — and rapidly — take place.
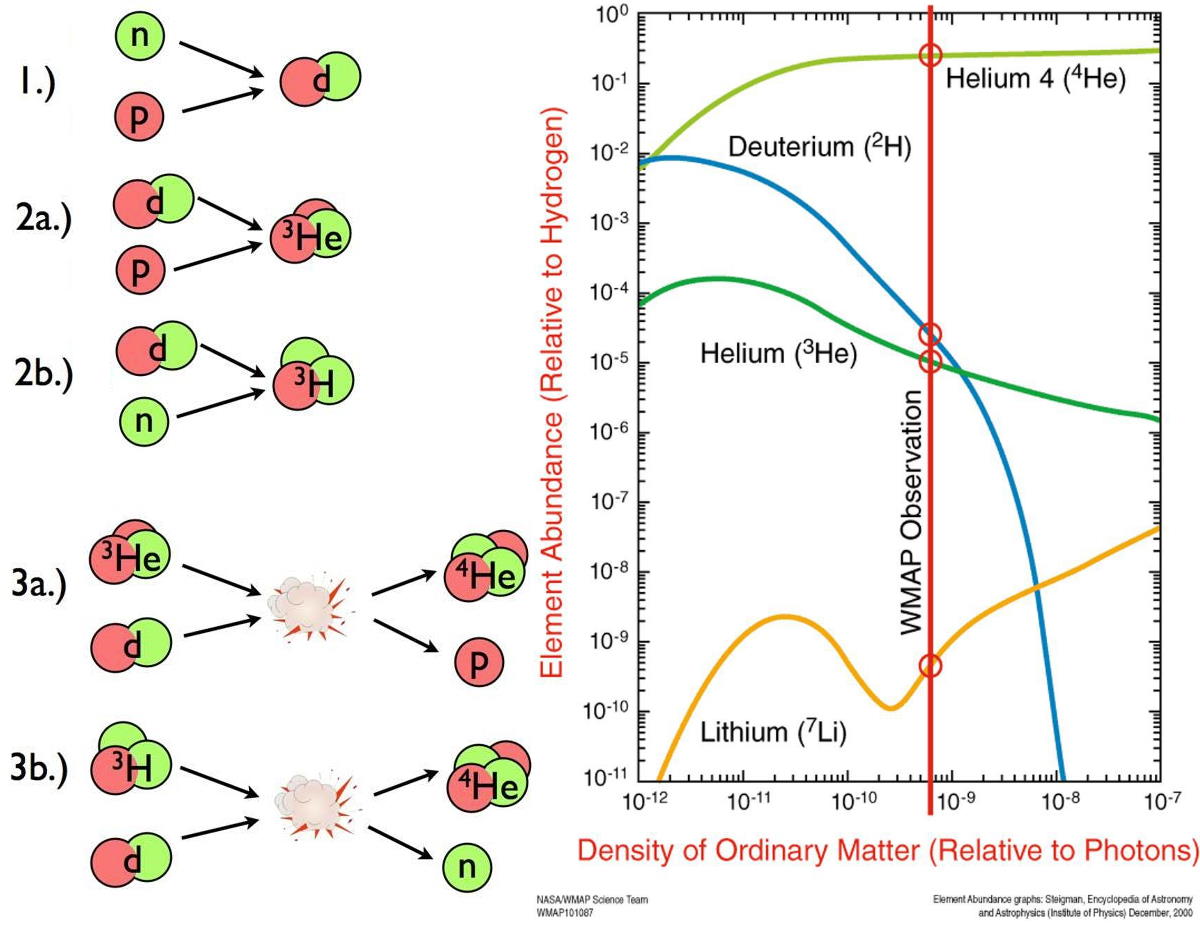
Almost immediately, neutrons begin finding protons, where they easily form deuterium. The Universe is still quite hot at this time: hundreds of millions of degrees, or much hotter than even the center of the Sun. But it’s not particularly dense; it’s only a fraction of the density of a star’s core. Deuterium will collide with a proton, producing helium-3, and then helium-3 will either collide with deuterium or another helium-3 nucleus, producing helium-4. In very short order, almost all of the neutrons find themselves in a helium-4 nucleus, with less than 1-part-in-1000 remaining as either deuterium or helium-3.
But this is pretty much the end of the story for the nuclear fusion reactions that occur in the early Universe: what we call Big Bang Nucleosynthesis.
- You can’t add a proton to helium-4, because every nucleus with a total of five nucleons is unstable.
- You can’t add another helium-4 nucleus to helium-4, because every nucleus with a total of eight nucleons is unstable.
- And although you can add a little bit of helium-3 to helium-4 to produce beryllium-7 (which will decay to lithium-7, but not for many centuries), that’s heavily suppressed due to electrical repulsion.
The densities are too low to get three nuclei colliding together at once (which is how helium fuses into carbon in the cores of evolved Sun-like stars), and so this is the end-of-the-line. At the end of Big Bang nucleosynthesis, the Universe is, by mass, about 75% hydrogen, 25% helium, about 0.01% each deuterium and helium-3, and about 0.0000001% lithium-7. These ratios remain unchanged until tens to hundreds of millions of years go by, and finally the first stars begin to form.

The defining feature of a star — i.e., what separates a “star” from “not a star” in the eyes of an astronomer — is whether it’s fusing light elements into heavier ones in its core. Although the Universe is “only” 75% hydrogen by mass when stars first begin forming, hydrogen is only one-quarter as massive as helium. If we instead decided to count atoms by number, we’d find that a whopping 92% of the atoms that existed after the Big Bang were hydrogen atoms.
In the cores of stars, incredibly high densities are achieved: about 150 times the density of water and substantially denser than the Universe was when fusion occurred during the hot Big Bang. However, temperatures only need to reach about 4 million K for nuclear fusion to commence. Without any free neutrons this time, we don’t start with deuterium, but only with protons. (Yes, there’s helium in there, but helium requires temperatures in excess of about 26 million K to begin fusing helium into carbon.)
So, what can you do to start things off? The first step is one that we considered — and rejected — when we were considering Big Bang nucleosynthesis: the fusion of a proton with a proton to start the chain reaction off. This is where it all begins in stars, but it doesn’t work the way most people think it would.
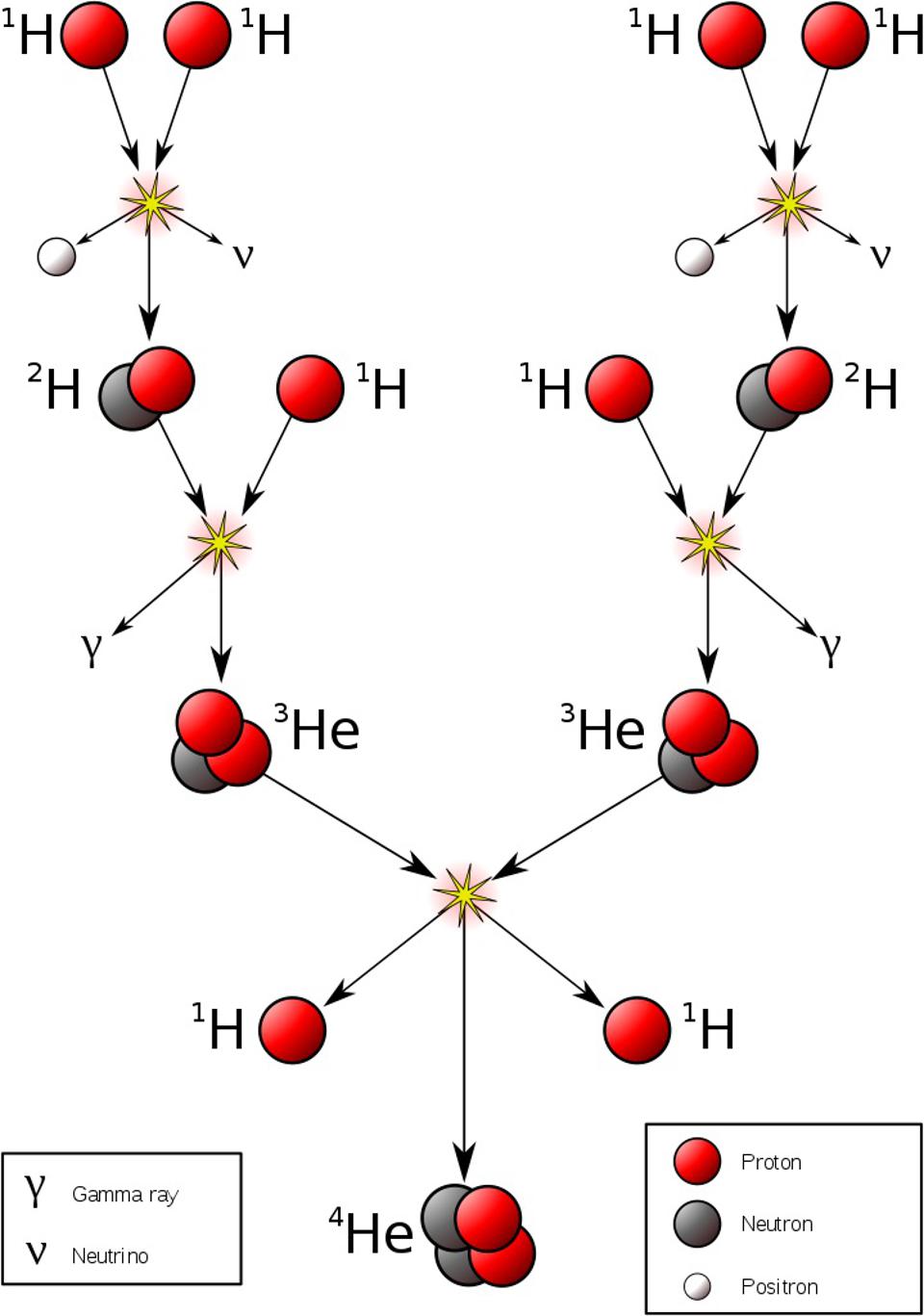
You might think, “Okay, I’m going to fuse a proton with a proton at these high temperatures, and that will make deuterium, plus whatever other things I need to conserve things like electric charge and other quantum quantities.” Deuterium, however, is made out of a proton and a neutron, and neutrons are more massive than protons. If you want to conserve charge, you also need a positron, and then if you want to conserve lepton number (another quantum rule), you also need an electron neutrino.
So you do your calculation. In the center of the Sun, or in the center of any Sun-like star, you know the temperature, you know the density, and you know the physics of how energy gets distributed over the particles that are inside. You can calculate collision rates as well as the energy of each collision, and based on how much extra “mass” you need to make all of the required particles to complete this reaction, you can see, via E = mc2, whether your collision has enough energy to make deuterium.
There are about ~1066 proton-proton collisions that happen in the Sun’s core each second. And of that number, exactly zero of them have enough energy to overcome the electrostatic repulsion between them and make deuterium.
The electric repulsion between the two positively charged particles is too great for even a single pair of protons to overcome it and fuse together with the energies in the Sun’s core. And yet, nuclear fusion happens, the Sun and all the stars emit these tremendous amounts of power, and somehow, hydrogen gets converted into helium. The secret is that, at a fundamental level, these atomic nuclei don’t behave as particles alone, but rather as waves, too.
Each proton is a quantum particle, containing a probability function that describes its location, enabling the two wavefunctions of interacting particles to overlap ever so slightly, even when the repulsive electric force would otherwise keep them entirely apart.
There’s always a chance that these particles can undergo quantum tunneling, and wind up in a more stable bound state (e.g., deuterium) that causes the release of this fusion energy, and allows the chain reaction to proceed. Even though the probability of quantum tunneling is very small for any particular proton-proton interaction, somewhere on the order of 1-in-10²⁸, or the same as your odds of winning the Powerball lottery three times in a row, that ultra-rare interaction is enough to explain the entirety of where the Sun’s energy (and almost every star’s energy) comes from.
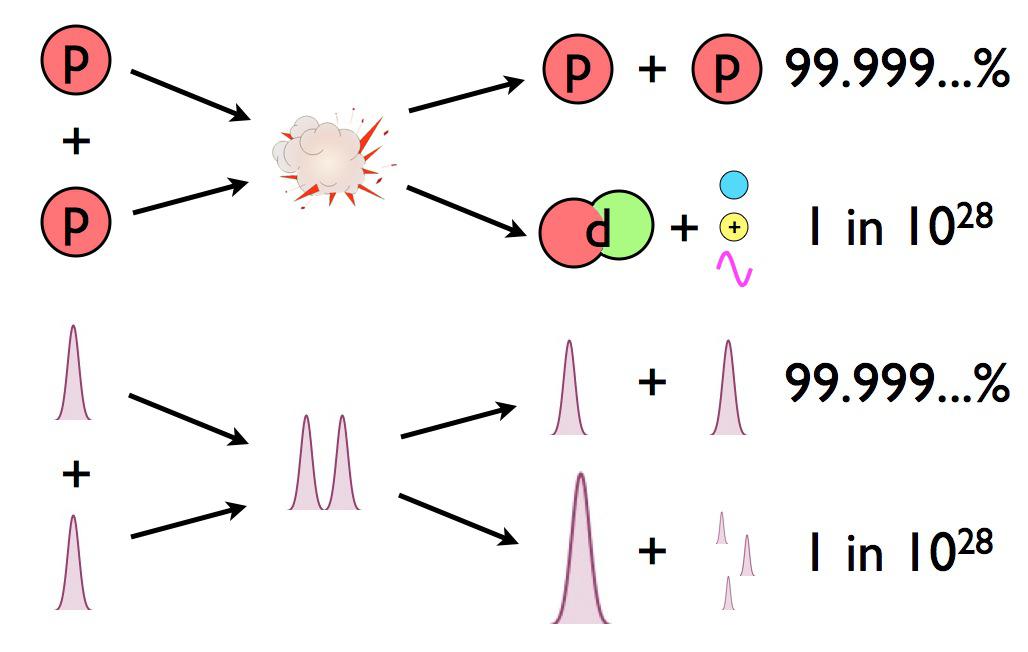
In other words, it’s only through the process of quantum tunneling, from a two-proton state to a deuteron plus additional particles, that enables deuterium to form via nuclear fusion. Once deuterium is made, however, things proceed very rapidly, but by multiple different pathways, up a series of reactions known as the proton-proton chain. But typically, the next step is that proton fuses with deuterium, creating helium-3. After that, helium-3 fuses with either deuterium or another helium-3 to create helium-4.
There are other variants of the proton-proton chain that occur at various energies, and once you have carbon, nitrogen, and oxygen, a process known as the CNO cycle occurs. In the CNO cycle, protons get added to carbon and then nitrogen (and sometimes even oxygen, for very hot stars), and radioactive decays then ensue, eventually recovering a carbon-12 nucleus and a helium-4 nucleus, the latter of which results from all of the added protons plus radioactive decays. In the Sun, only about 1% of our energy comes from the CNO cycle, but once you get about 30-40% more massive than the Sun, the CNO cycle dominates over the proton-proton chain.

At the end of Big Bang nucleosynthesis, the Universe was about 75% hydrogen and 25% helium. In all the stars that have formed in the ensuing 13.8 billion years, about 5% of the hydrogen has been fused into helium, and perhaps 1-2% of that helium has been fused into all of the heavier elements combined, dominated by oxygen and carbon. The biggest differences in the fusion reactions that occurred in the early Universe versus the ones that occurred later, in stars, are:
- most of the first-step fusion reactions in the Big Bang were protons fusing with neutrons, rather than protons with protons,
- the temperatures were much higher during Big Bang nucleosynthesis than they are in all but the most massive of stars,
- the densities were much lower during the Big Bang than they are in stars,
- and the process where photons blast deuterium nuclei apart is a major player in the early Universe, but is all but completely irrelevant in the interiors of stars.
If the free neutron, by itself, weren’t an unstable particle, the entirety of the cosmic story of the elements would have been vastly different. If the neutron had the same mass as the proton, our Universe would have been ~100% helium after Big Bang nucleosynthesis, with hardly any hydrogen at all. Similarly, if the neutron were significantly more unstable, and had a half-life that was measured in seconds rather than minutes, there would have been practically no Big Bang nucleosynthesis happening, and our Universe would have been left with ~100% hydrogen for stars to work with.
It’s only because of the properties our Universe had that we wound up with the elements we possess today. For that, yes, you should thank your lucky stars, but also the Big Bang and the properties of the laws and rules that govern the Universe itself. Without it all, the cosmos would have simply been an awful waste of space.
Send in your Ask Ethan questions to startswithabang at gmail dot com!