Ask Ethan: Does space require dark energy in order to exist?

Here in our Universe, one of the few things we can be certain of is that every signal we’ve ever observed has originated within the fabric of spacetime itself. Galaxies, stars, planets, atoms, particles and antiparticles, photons, gravitational waves, and more all exist within, and propagate through, the fabric of space, affecting everything they encounter. Although it’s difficult, it is possible to find regions of space that are exceedingly empty: with only the smallest traces of matter and radiation found in the deepest voids in intergalactic space. However, even in those regions, space itself not only has no problem continuing to exist, but the fabric of spacetime itself continues to expand, just as it does throughout the rest of the Universe.

Is there something profound about this? Does it mean that space and the energy that cannot be extracted from it — also known as dark energy — depend on one another for their mutual existence? That’s the question of Allan Hall, who asks:

“If you could remove all baryonic and dark matter from space it seems to me that space itself would still exist. I understand that dark energy is characterized as the ‘fabric’ of space and is what has driven expansion from the beginning; but is space dependent upon dark energy for its (and the universe’s) existence?”

Can space exist without dark energy? It’s a profound question, it gives us a lot to consider. Let’s dive in!

In theory, the Schwinger effect states that in the presence of strong enough electric fields, (charged) particles and their antiparticle counterparts will be ripped from the quantum vacuum, empty space itself, to become real. Theorized by Julian Schwinger in 1951, the predictions were validated some 70 years later in a tabletop experiment, using a quantum analogue system. Whether space can exist without these fields, or the energy that they possess in their ground state, is not yet answered.

There are two ways, fundamentally, to look at the fabric of space itself: from the perspective of quantum fields, and from the perspective of Einstein’s general relativity. In each of these scenarios, there’s an understanding of what space is that are similar, but not identical, to one another. There’s also, in each of these pictures, a chance for space to have an inherent, non-zero energy to it everywhere, that are again not identical to one another. Finally, there’s what we know about our Universe from an observational perspective, which is what we base our understanding of dark energy on at present, and which makes us so confident that it does indeed exist.

The big question — and I’ll even fess up that it’s a big unanswered question at this point in time — is how these three different perspectives:

• the quantum field theory perspective,
• the general relativity perspective,
• and the observational perspective,

are all related to one another. We can come up with a consistent explanation that ties all three together, but there’s no guarantee that’s a reflection of what nature is actually doing, rather than a potential limitation in our theoretical understanding of how the Universe works. Part of the reason this is such an interesting question is that, fundamentally, we have only a very coarse understanding of dark energy itself: both observationally and theoretically. Here’s an outline of the trouble we face.

A few terms contributing to the zero-point energy in quantum electrodynamics. The development of this theory, due to Feynman, Schwinger, and Tomonaga, led to them being awarded the Nobel Prize in 1965. These diagrams may make it appear as though particles and antiparticles are popping in and out of existence, but that is only a calculational tool; these particles are virtual, not real.

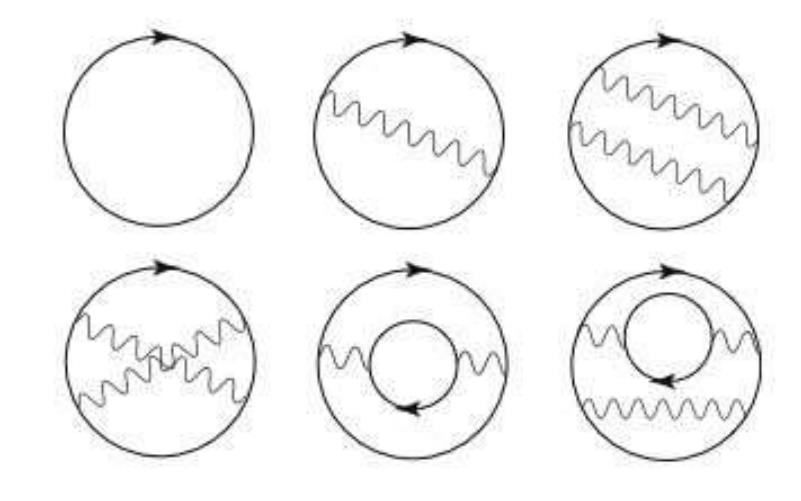
Quantum field theory

In the 20th century, perhaps the biggest change in our understanding of how the Universe works came in the form of the quantum revolution. Reality, as we now understand it, consists of various quanta — particles, antiparticles, and bosons — that propagate through the fabric of space. Everything behaves as a particle when it interacts, even light itself, which is composed of individual “packets” of energy (i.e., photons) rather than a continuous wave-like stream. In our Universe, as far as we understand it, everything is inherently quantum.

This doesn’t just apply to the quanta that make up reality as we know it, but also to the fields that permeate all of space. Every particle with a charge:

• a color charge, for the strong force (possessed by quarks, antiquarks, and gluons),
• a weak isospin or weak hypercharge, which includes all quarks, antiquarks, leptons, antileptons, plus the W-and-Z bosons,
• an electric charge, including all quarks and antiquarks, the charged leptons and antileptons, plus the W (but not the Z) bosons,
• or even (theoretically) a gravitational charge, such as mass or an inherent amount of energy, applying to all particles and antiparticles,

interacts with the quantum fields that pervade our Universe, and those fields cannot be extricated from space itself.

As electromagnetic waves propagate away from a source that’s surrounded by a strong magnetic field, the polarization direction will be affected due to the magnetic field’s effect on the vacuum of empty space: vacuum birefringence. By measuring the wavelength-dependent effects of polarization around neutron stars with the right properties, we can confirm the predictions of virtual particles in the quantum vacuum.

One of the tremendous realizations of 20th century physics was that these quantum fields continue to persist throughout all of space at all times: even in the absence of any charges that could generate them. This shows up experimentally, in various forms, including:

• vacuum polarization/birefringence, where empty space itself becomes polarized due to an external magnetic field,
• the Casimir effect, where two conducting plates placed in a vacuum feel a net force between them due to the excluded virtual modes of the electromagnetic fields,
• and the Schwinger effect, where a strong electric field can pull particle-antiparticle pairs out of empty space itself and cause them to become real.

According to quantum field theory, that’s because all of these (quantum) fields always exist throughout all of space, and cannot be separated from it, even in the absence of quanta that carry the charges of that field. You’ve likely seen illustrations of “particles popping in-and-out of existence” or some sort of randomly fluctuating field shown to be inherent to space itself, and while that’s certainly an eye-catching interpretation, it isn’t necessarily technically correct. Instead, what you should consider as a more accurate picture is that these fields are always there, omnipresently, and that it’s only when an external influence comes in — particles/antiparticles, an external field, boundaries, etc. — that you’re going to observe the effect of the field’s presence.

Visualization of a quantum field theory calculation showing virtual particles in the quantum vacuum. (Specifically, for the strong interactions.) Even in empty space, this vacuum energy is non-zero. If there are additional particles or fields beyond what the Standard Model predicts, they will affect the quantum vacuum and will change the properties of many quantities away from their Standard Model predictions. However, the QCD contribution cannot be calculated perturbatively, the way electromagnetism can.

However, the fact remains that these fields are always there, and cannot be “removed” or “extracted” from space in any way. All fields have what’s known as a ground state, or a lowest-energy state that they can occupy. When you take everything else away — including particles/antiparticles, fields, boundaries, etc. — that’s what remains. Known as:

• the ground state,
• the zero-point energy state,
• the lowest-energy state,
• or simply as the quantum vacuum,

this is a property that’s inherent to all systems, but one that comes along with an existential difficulty: we have no idea how to calculate what this amount of energy actually is, or what value it ought to take on.

In string theory, for example, there are an enormous number of possible vacuum states (at least ~10⁵⁰⁰), and the only way to know which one describes your particular Universe is to measure it. Many have tried to calculate, through summing the various Feynman diagrams arising in quantum field theory, to calculate contributions to the quantum vacuum directly; unfortunately, this yields values for those calculable terms that are roughly a factor of ~10¹²⁰ too large in magnitude. Many posited that, “Well, these diagrams must all somehow cancel, yielding a zero-point energy that’s exactly zero,” but there is no support for this idea; it’s just a hunch at this point.

In summation, quantum field theory tells us there can be a finite, non-zero value for the amount of energy inherent to space, but we haven’t advanced our understanding of the Universe sufficiently to know what that value ought to be, or how to calculate it.

Instead of an empty, blank, three-dimensional grid, putting a mass down causes what would have been ‘straight’ lines to instead become curved by a specific amount. In general relativity, we treat space and time as continuous, but all forms of energy, including but not limited to mass, contribute to spacetime curvature. In addition, the distances between unbound objects evolve with time, owing to the expansion of the universe.

General relativity

On the other hand, we have our non-quantum theory of gravity, general relativity, that describes our Universe exquisitely well in every regime where we’ve been able to subject it to the critical tests. Instead of a quantum picture of reality, general relativity weaves together space and time into a fabric that curves, ripples, and can expand-or-contract depending on the distribution of all the various types of matter and energy that are present within it. Large sources of mass — like galaxies, stars, and black holes — can cause space to curve severely, and that curved space then tells all other forms of matter and energy that exist or propagate within that curved space how they’re going to move and evolve in the future.

Again, just as in the case of quantum field theory, we can do our best to remove absolutely everything from as large a region of space as we desire: all forms of matter and antimatter, all nearby sources of mass, all types and species of radiation, whatever the unknown dark matter turns out to be, etc. Take it all away, as far away as you care to imagine it, until all you have left is the vast void of empty space itself. You’ll find, just as you did previously, that there’s one species of energy that, if it turns out to be non-zero, you cannot get rid of from the Universe in any way: the cosmological constant, or a form of energy that’s inherent to space itself.

While matter and radiation become less dense as the Universe expands owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant.

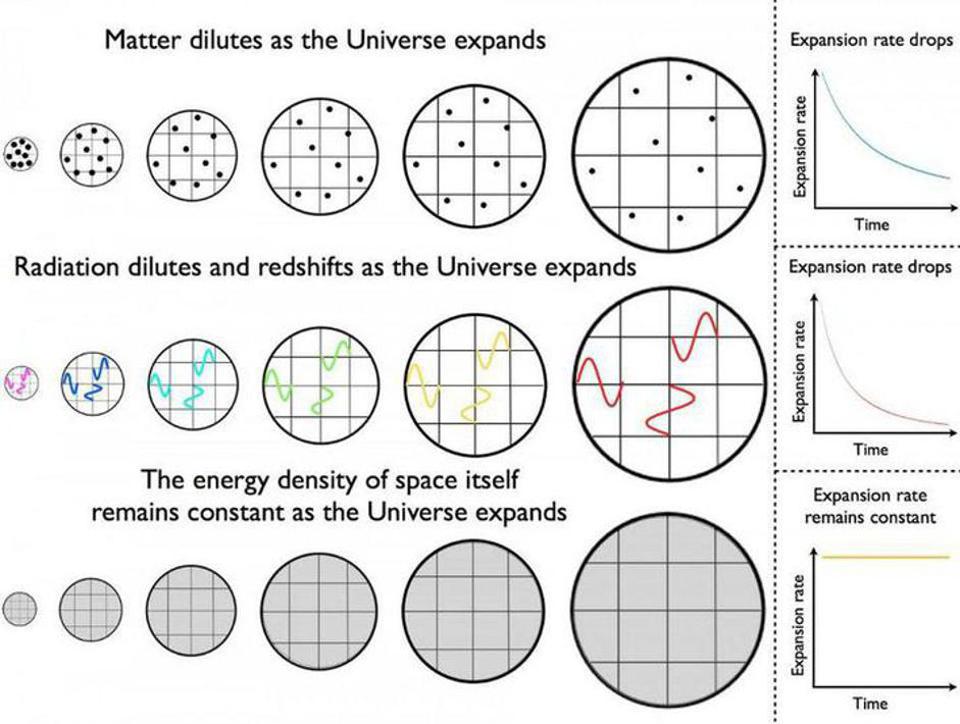
The cosmological constant has an interesting history: it was first inserted by Einstein into his equation in order to prevent the Universe from either expanding or contracting, as without it, any gravitational system of masses would be inherently unstable, doomed to either collapse into a singularity or expand into oblivion. Given the discovery of the expanding Universe in the late 1920s, Einstein came to eventually call his introduction of the cosmological constant his greatest blunder, although there’s nothing wrong with a Universe that possesses a non-zero cosmological constant. There was just no reason to assume it had any value other than zero.

But in general relativity, the only way to know something’s value is to measure it. There are no dynamics of the theory itself that determine what the value of the cosmological constant is; the theory can only describe how spacetime responds to its presence. If there’s a positive cosmological constant, it causes space to expand no slower than a specific, positive, relentless rate, even in the absence of all other forms of matter and energy. Similarly, if the cosmological constant is negative, it causes space to contract in exactly the opposing fashion. Unlike all other forms of matter-and-energy, a cosmological constant’s energy density never dilutes or changes. It simply remains constant.

In summation, general relativity admits the possibility that there’s a positive, non-zero energy that’s inherent to and inextricable from the fabric of space itself, but it, too, gives us no way to calculate what the value of that amount of energy is, and no answer to the question of whether it’s related to the value of the zero-point energy of space that comes from quantum field theory.

The matter and energy content in the Universe at the present time (left) and at earlier times (right). Note how dark matter and dark energy dominate today, but that normal matter is still around. At early times, normal matter and dark matter were still important, but dark energy was negligible, while photons and neutrinos were also quite important. The expansion rate is determined by the actual, instantaneous value for density, not by the distribution of the pie chart.

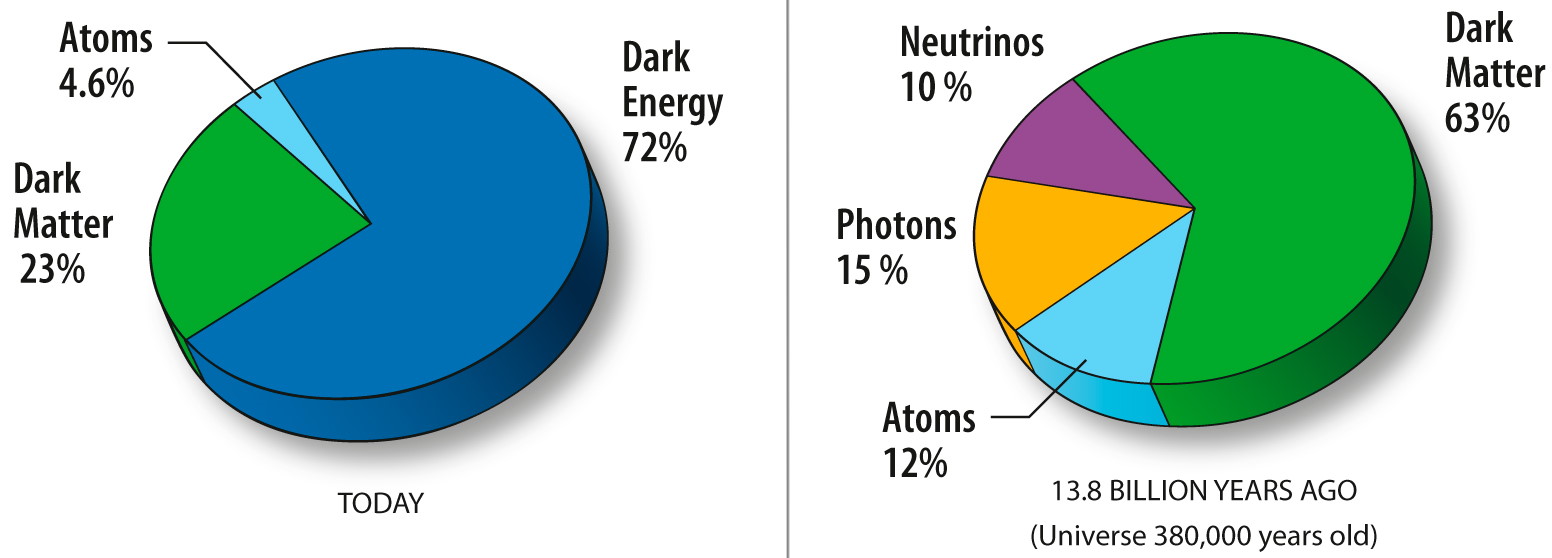
Observational properties of dark energy

Finally, we come face-to-face with the one thing that all physical theories must inevitably be confronted with: observations of reality itself. We can put the question to the Universe of, “What are you made of?” simply by simultaneously:

• understanding the equations, derived from general relativity, that govern the expansion of the Universe,
• and then using a variety of measurement probes to see how our Universe has actually expanded over cosmic history.

Because of the intricate relationship between how spacetime curves, expands, and evolves and the distribution and density of all forms of matter-and-energy within the Universe, making these measurements enables us to know what the Universe is made of.

Cosmological probes include, but are not limited to:

• the cosmic microwave background, which is the leftover glow from the Big Bang,
• a feature known as baryon acoustic oscillations, which gives us a distance scale (that expands along with the Universe) that describes galaxy-galaxy clustering and is measurable through the large-scale structure of the Universe,
• and distant objects, including quasars and galaxies, that can have some intrinsic property of them measured and known, along with their redshift and distance from us.

When we piece together the evidence from a great many lines of evidence, including all three of these, we arrive at an inescapable picture of our Universe: one that contains normal matter, radiation, and neutrinos, but where all of that, combined, makes up only 5% of the total energy in the Universe. 27% of the total energy is massive but not part of the Standard Model: the mysterious type of energy known as dark matter. The remaining 68%, or “most of the Universe” according to Nobel Laureate Adam Riess, is what we know today as dark energy.

If dark energy is not a constant over time, then it shouldn’t be described by a single parameter, w, but rather by two or more parameters that allow an evolution with time. In this figure, the intersection of the dotted lines correspond to a simple cosmological constant for dark energy; the DESI data, when combined with CMB and/or supernova data, strongly favors an evolving form of dark energy that weakens over time. The case where w0 = -1 and wa (or w’) = 0 corresponds to constant dark energy.

Nearly all of our measurements indicate that dark energy behaves as a cosmological constant, although there is some recent data from baryon acoustic oscillations that seems to indicate that dark energy was a constant for most of the Universe’s history, but may be slightly weakening in recent times: over only the past few billion years. If dark energy evolves in its strength — i.e., in its energy density — over time, then we can’t rightfully identify it with either the zero-point energy of space from quantum field theory or with the cosmological constant from general relativity. Only if dark energy is truly a constant, both in space and across cosmic time, do either of these descriptions match up with our understanding of how the Universe actually plays out.

We have only one instance in cosmic history where the amount of energy inherent to space itself appeared to change: at the end of cosmic inflation, and, correspondingly, to the onset of the hot Big Bang. During cosmic inflation, there’s strong evidence that the Universe was dominated by a period of energy not only being inherent to space, but of being tremendous: of having a value that’s many orders of magnitude (at least a factor of ~10¹⁰⁰) greater than the value of dark energy today. When inflation comes to an end, the overwhelming majority of that energy gets converted into various quanta: things like matter, antimatter, and radiation.

Somehow, however, it appears that the end of inflation didn’t drive the value that the energy inherent to space possesses (dark energy) down to zero, but rather to a small, positive, but non-zero value: the value we observe it to take on today.

A scalar field φ in a false vacuum. Note that the energy E is higher than that in the true vacuum or ground state, but there is a barrier preventing the field from classically rolling down to the true vacuum. Note also how the lowest-energy (true vacuum) state is allowed to have a finite, positive, non-zero value. The zero-point energy of many quantum systems is known to be greater than zero, and nobody knows if today’s observed dark energy is due to a true vacuum or false vacuum state.

Those are the three pieces of information we have about the energy inherent to space itself. We can identify this value with:

• the zero-point energy of space in quantum field theory,
• the value of the cosmological constant in general relativity,
• or the strength of dark energy within our observable Universe today, which decreased at least once, and tremendously at that, from the much larger value it took on during cosmic inflation.

Unfortunately, that’s as far as we’ve been able to come in terms of understanding what’s responsible for the energy that appears to be inherent to space.

Can this energy somehow be extracted from space, after all, and would space continue to exist without it? That would lead to a vacuum decay scenario, which would be catastrophic for life, planets, stars, atoms, and more, but it’s not impossible, and it wouldn’t cause space to stop existing. Is dark energy evolving or weakening over time? If so, then it isn’t something we can identify with either the zero-point energy or the cosmological constant, but rather is some type of field whose value is not fixed, implying that space can exist without it.

But if dark energy is truly a constant, then we can justifiably hypothesize that perhaps the quantum vacuum from quantum field theory, the cosmological constant from general relativity, and the observed phenomenon that we see as dark energy are all indeed the same thing: a measure of the inextricable energy that cannot be removed from empty space itself, no matter what you do. Can space exist without it? Unless dark energy turns out to truly evolve, the best answer we can give is, “If that’s the case, we haven’t seen evidence for it yet.”

Send in your Ask Ethan questions to startswithabang at gmail dot com!