New theoretical calculation solves the “muon g-2” puzzle

- For several years, attempts to measure the magnetic moment of the muon have led to an interesting anomaly: a slight, but significant, departure from theoretical predictions.
- An experiment initially begun at Brookhaven has since moved to Fermilab, where it’s gotten far more precise: to the point where the difference between theory and experiment now approaches the 5-sigma “gold standard” for discovery.
- But rather than “break the Standard Model,” a team using an arguably superior theoretical method of calculating the expected magnetic moment — Lattice QCD — asserts the problem lies with the earlier theorists. Their new calculation causes the anomaly to vanish.
As a scientist, the most exciting moments in your professional life arise when you work hard to get a result, and — no matter how hard you try to understand it — it simply doesn’t match up with your expectations. For theorists, that moment comes when you derive a result that conflicts with what’s experimentally and observationally known to be true. For experimentalists, that moment arrives when you make a measurement that defies a theorist’s predictions. But those moments can go one of two ways: either they can be harbingers of a scientific revolution, exposing a crack in the foundations of science, or they can simply be the result of a previously undiscovered error, on either the theoretical or experimental ends.
Perhaps the greatest quest in particle physics, for perhaps half a century now, has been to find a discrepancy between theory and experiment when it comes to the Standard Model. One fascinating place to look is at the magnetic moment of the muon: a heavy, unstable relative of the electron. A Fermilab experiment known as “muon g-2″ has revealed a discrepancy between theory and experiment at greater than the 4-sigma level: approaching the gold standard for discovery. But is this evidence for new physics?
According to a new theoretical calculation, the answer is no: it’s a flaw in the technique used by the majority of the theoretical community. Using new lattice QCD techniques, theory and experiment align, suggesting that the puzzle has finally been solved. Here’s how.

What is g, the magnetic moment of the muon?
Imagine you had a tiny, point-like particle, and that particle has an intrinsic electric charge to it. Despite the fact that there’s only an electric charge — and not a fundamental magnetic one — that particle is going to have magnetic properties, too. Whenever an electrically charged particle moves, it generates a magnetic field. If that particle either moves around another charged particle or spins on its axis, like an electron orbiting a proton or the Earth rotating as it orbits the Sun, it will develop what we call a magnetic moment: where it behaves like a magnetic dipole. This is a behavior that’s been familiar to physicists since the 19th century: back from the days of classical electromagnetism.
Now, we don’t have a classical universe when it comes to fundamental particles; we have a quantum one. In quantum mechanics, point particles don’t actually spin on their axis, but rather behave like they have an intrinsic angular momentum to them: what we call quantum mechanical spin. The first motivation for this came in 1925, where atomic spectra showed two different, very closely-spaced energy states corresponding to opposite spins of the electron. This hyperfine splitting was explained 3 years later, when Dirac successfully wrote down the relativistic quantum mechanical equation describing the electron.
If you only used classical physics, you would’ve expected that the spin magnetic moment of a point particle would just equal one-half multiplied by the ratio of its electric charge to its mass multiplied by its spin angular momentum. But, because of purely quantum effects, it all gets multiplied by a prefactor, which we call “g.” If the Universe were purely quantum mechanical in nature, g would equal 2, exactly, as predicted by Dirac.

If g is supposed to be 2, then why are we performing a “g-2″ experiment?
As you might have guessed, g doesn’t equal 2 exactly, and that means the Universe isn’t purely describable by old-school quantum mechanics. In quantum mechanics, particles are quantum, but fields are classical. The advance of quantum field theory overruled and superseded that picture: not only are the particles that exist in the Universe quantum in nature, but the fields that permeate the Universe — the ones associated with each of the fundamental forces and interactions — are quantum in nature, too. An electron experiencing an electromagnetic force won’t just attract or repel from an interaction with an outside photon, but can exchange arbitrary numbers of virtual and even real particles, all according to the probabilities you’d calculate in quantum field theory.
When we talk about “g-2” for any particle, like an electron (but also for other particles), we’re talking about all the contributions from everything other than the “pure Dirac” part. That includes everything associated with:
- the electromagnetic field,
- the weak (and Higgs) field,
- as well as the contributions from the strong (QCD) field.
In 1948, Julian Schwinger — a co-inventor of quantum field theory along with Feynman and Tomonaga — calculated the largest contribution to the electron and muon’s “g-2:” the contribution of an exchanged photon between the incoming and outgoing particle. This contribution, which equals the fine-structure constant divided by 2π, was so important that Schwinger had it engraved on his tombstone.

Why do we care about “g-2″ for the muon?
Any particle, either fundamental or composite, that has an electric charge (or even that just has charged components inside, like a neutron) is going to have a magnetic moment. You might think that the electron would be the best particle to use, since it’s a fundamental, point-like, and stable particle. But at only 1/1836th the mass of a proton, its mass-to-charge ratio is very low (or its charge-to-mass ratio is very high), which means that the effects of “g-2″ are dominated by the well-known and easy-to-calculate electromagnetic force. We’ve made that measurement and calculated that theoretical prediction, for the electron, to 13 significant figures. As Wikipedia notes, the electron’s magnetic moment is “the most accurately verified prediction in the history of physics.”
The muon, on the other hand, is very similar to the electron, with the two biggest differences being that:
- it’s unstable, with a mean lifetime of 2.2 microseconds,
- and that it’s heavy, weighing in at 206 times the mass of the electron (or just about 11% of a proton’s mass).
Overall, its magnetic moment is smaller than that of the electron, but its heavier mass means that the strong force contributes much more greatly to the muon’s magnetic moment than the electron’s magnetic moment. Whereas the electron is agnostic about the strong force at current precisions, these effects show up for the muon at the 1-part-in-a-billion (10⁹) level. And those effects are precisely what the Muon g-2 experiment, at Fermilab, is working on measuring.
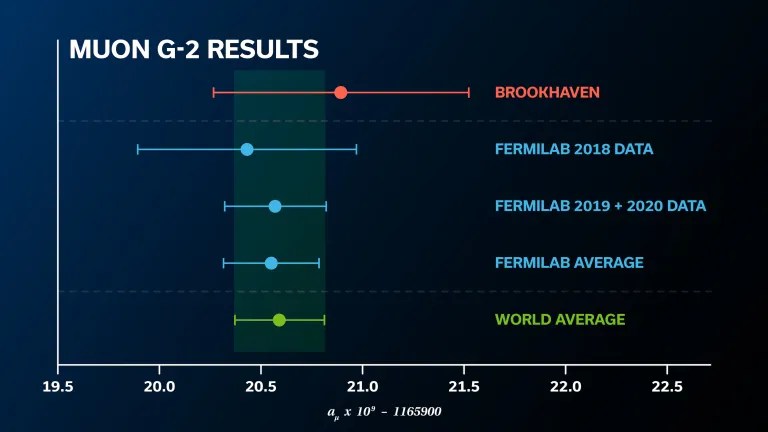
The Fermilab experimental results
Wherever you have very precise predictions and the capability of gleaning very precise experimental results, it’s an experiment you simply have to do: it’s a chance to test nature to the greatest precision of all-time in a way it’s never been probed before. If there’s an anomaly — i.e., a mismatch between theoretical predictions and experimental results — it just might be a hint of new physics, and some types of new physics that could contribute to the muon’s magnetic moment include:
- new particles,
- new fundamental forces,
- or, as has been suggested, a new phenomenon occurring within the quantum foam of the universe.
That’s why the Muon g-2 experiment is so important, and why we have to pay very close attention to the experimental results that the collaboration obtains from it.
In April of 2021, the muon’s g-2 was measured to be 0.00233184080, with an uncertainty of ±0.00000000108 attached to it. From new results that were announced in August of 2023, an improvement in the measured g-2 was achieved, determining it to be 0.00233184110 ± 0.00000000047, with a greatly reduced uncertainty. It’s a monumental experimental achievement to measure something this challenging to such great precision, but the true test comes from comparison with theoretical predictions.
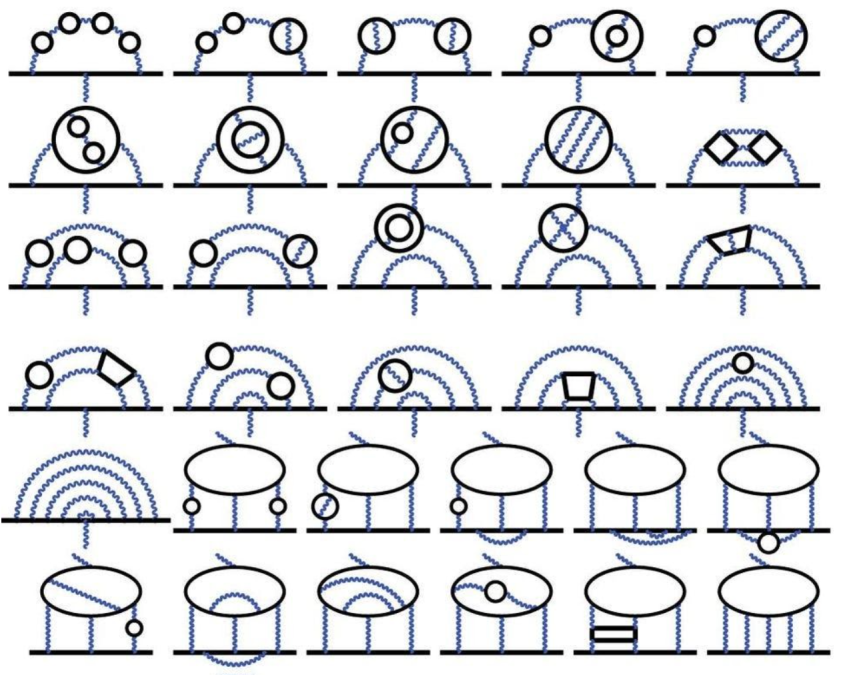
The general theoretical method
When it comes to calculating quantum electrodynamic effects, it’s a pretty straightforward procedure, although not an easy one. What you do is you quantify:
- how electromagnetism works for the electron at tree level (with no loops in your Feynman diagrams),
- how it works at one-loop order (with up to one electron and/or photon loop in your diagrams),
- how it works at two-loop order,
- etc.,
until you reach the precision you want to achieve. For the electron, this gets you pretty much everything you’d ever want to know about its magnetic moment, also known as its gyromagnetic ratio, which is where the letter g comes from. Modern calculations have gone up to six-loop order and beyond.
But for the muon, due to its higher mass (and identical charge) as compared with the electron, quantum chromodynamic effects start to come into play. When it comes to the effects of the strong nuclear force — the contributions of quarks, gluons, and all composite interactions (such as from mesons and baryons) — this is not easy to calculate. In fact, the way we calculate the effects of the weak and electromagnetic interactions, which is to calculate the contributions from progressively more and more complex interaction diagrams, will not work for the strong interactions. That is because the strong interactions are what we call non-perturbative: you can’t simply calculate greater and greater loop-order diagrams to get greater and greater accuracies. We have to resort to other means.

The experimental input method: also known as the r-ratio method
Unlike all of the other Standard Model interactions, the strong force gets weaker at short distances rather than stronger: it acts like a spring rather than like gravity. We call this property asymptotic freedom: where the attractive or repulsive force between charged particles approaches zero as they approach zero distance from one another. This, coupled with the large coupling strength of the strong interaction, makes the common “loop-order” method, which works well for both the electromagnetic and the weak interactions, wildly inappropriate for the strong interaction. The more diagrams you calculate, the less accurate you get.
What the r-ratio method does, instead of attempting to calculate the strength of the contribution to the muon’s gyromagnetic ratio, g, is instead to infer it based on previously measured experimental inputs. The positive aspect to using this method is that, by performing experiments over and over again, you can obtain very small statistical errors, giving you a low uncertainty for these inputs. But the negative aspect is that you’re using experimental results in one regime to infer a theoretical contribution in a different regime: a method that may induce systematic errors that you cannot easily identify. If this occurs, it will “shift” the value of your theoretical prediction, and may give you a mismatch between theory and experiment where none is actually present.
Please note, importantly, it was by comparing the Muon g-2 experiment’s result with this theoretical prediction that the earlier claims for a mismatch at such high significance were made.
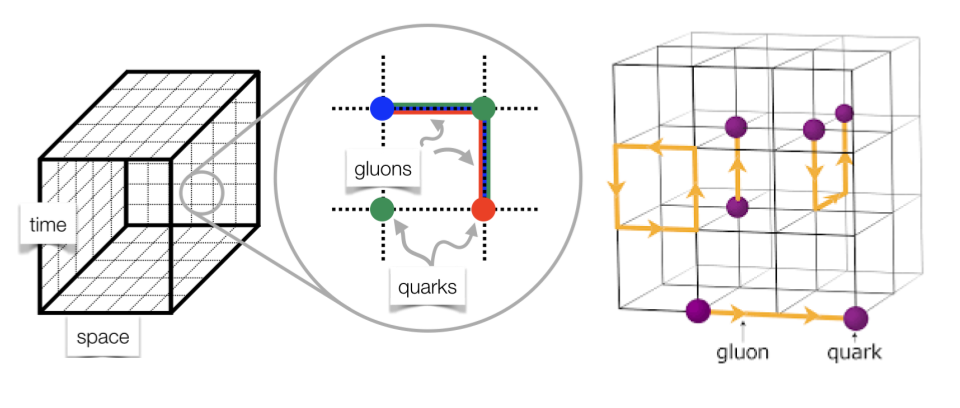
The superior method: lattice QCD
Instead of using experimental inputs, one can actually try to calculate, directly, the contribution of the particles and fields from the strong force to the muon’s magnetic moment. We can’t do these calculations by writing down diagrams and calculating them to higher and higher precisions (and with greater numbers of loops in them), as that method only works for perturbative theories. However, there is a non-perturbative approach: lattice QCD. It’s called lattice QCD because it’s a gauge theory formulated on a grid (lattice) of points in space and time. If you could both:
- make your lattice infinitely large in size,
- but the spacing between your lattice points infinitely small in size,
you would be able to calculate theoretical results in QCD, the theory of the strong force, exactly.
Of course, that’s not practically possible, but with enough computing power and a sufficiently efficient algorithm, we can get progressively more and more accurate results using this method. We are not limited by experiments or their range of applicability when it comes to lattice QCD; just by computational power. What’s very important here is that, starting in 2020, lattice QCD predictions started to get better and better, and began to show a significant discrepancy with the experimental input (r-ratio) method, but showed that they were in agreement with Fermilab’s experimental results.
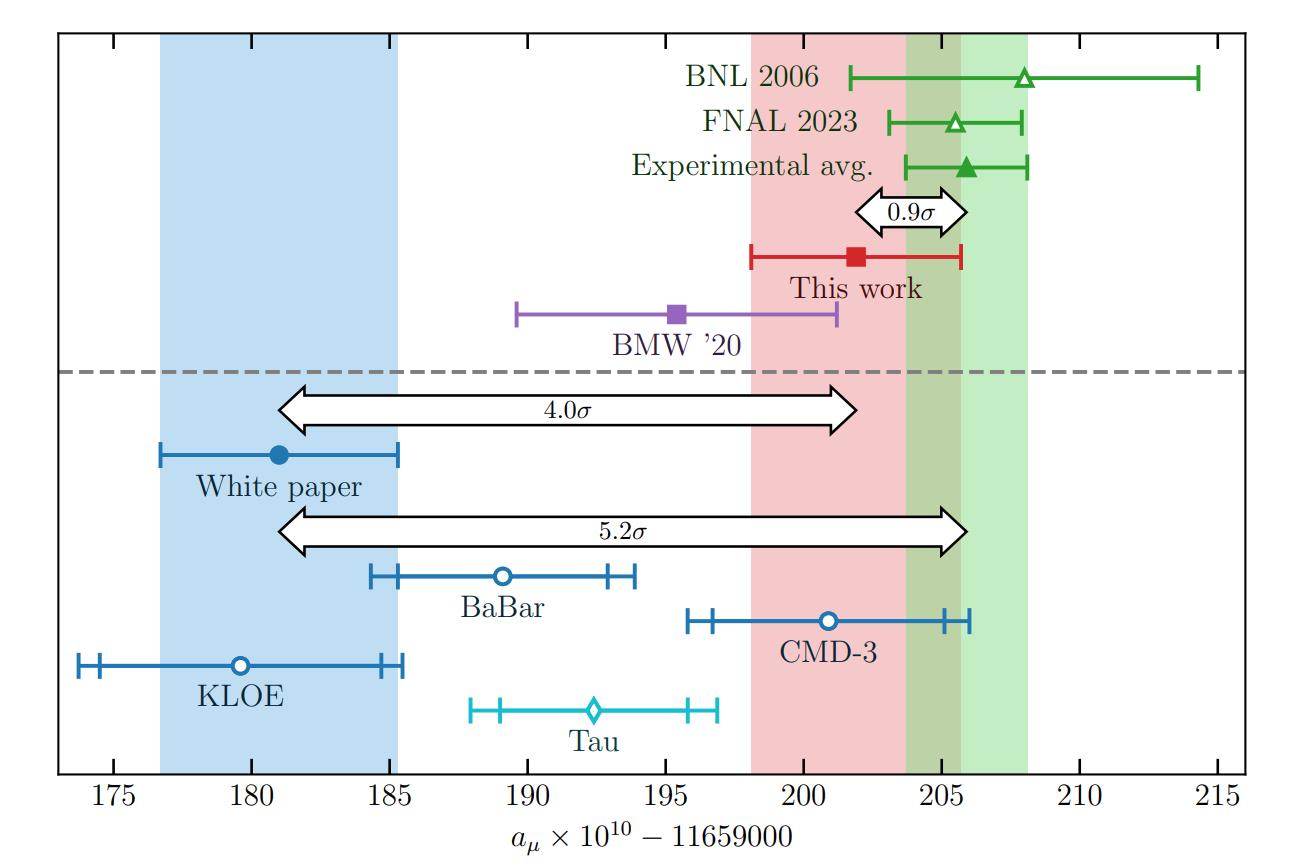
The new, superior lattice QCD calculation
And now, at last, we come to the present day, and new science here in July of 2024. What you see, above, is what I would call the “money plot” from this recent paper: a new lattice QCD calculation that includes the hadronic (strong force, quark-and-gluon based, QCD) contribution to the muon’s magnetic moment. As you can clearly see, the errors and uncertainties are small, and smaller than they’ve ever been for a lattice QCD calculational method to theoretically compute the muon’s magnetic moment, and hence, g-2. The big advance, driven by an increase in computational power, is that the simulations being performed are now done on finer, more closely-spaced lattices than ever before.
Whereas the r-ratio method gave results that differed from the experimental Fermilab results at the 5.2-sigma level, they disagree with lattice QCD results at 4.0-sigma significance. Meanwhile, the lattice QCD results agree spectacularly with the latest experimental results from Fermilab, and “disagree” at only the 0.9-sigma level, which is not at all significant. (About 35% of all random samples will disagree with the “true value” at the 0.9-sigma level.)
While many hoped that the g-2 experiment would finally break open the Standard Model and reveal never-before-seen hints of new particles, fields, or forces, what it instead did was show us the insufficiency of an earlier method of calculating our theoretical expectations for the value of g for muons, and showed how lattice QCD calculations were the necessary missing piece to make correct predictions.

Of course, there are reasons we do the experiments: we need to know what nature is actually telling us. We should never assume that the Standard Model — or any theoretical expectation — is what nature is going to wind up giving us; our best theories at any moment in time can only ever represent a successful (so far) approximation of reality. At some level, we know that we do not have the full story regarding the Universe worked out yet, and we don’t know where departures from our best picture of reality will come from. To that end, it’s very important to keep calculating things to the greatest precisions we can muster, and to ensure that we’re making the best measurements and observations that modern technology permits.
But we also have to be very, very careful. It’s all too easy to detect one anomaly and declare, “There must be a new fundamental force, a new type of particle, or a new field present here,” when that’s far from the case. Most often, we’ve simply committed a hitherto unidentified error, and it’s up to ourselves or the rest of the community to find where we went astray. No doubt, the r-ratio and lattice QCD communities will continue to fight over the true theoretical, expected value of the muon’s magnetic moment, and we all look forward to the day when these two methods lead to predictions that align. But right now, there’s a great puzzle over the value of the muon’s magnetic moment. If the lattice QCD community is right, that puzzle has finally been solved.