Why the black hole information paradox still hasn't been solved

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all

No matter what you do in the Universe or how you do it, the overall entropy within our cosmic horizon always increases. Even when we go through the effort to put things in order — assembling a puzzle, cleaning our houses, even (yes, it’s possible) unboiling egg whites — it will still only be the local entropy of that one isolated component of the total physical system that decreases. In order to accomplish these feats, we have to expend energy, and that expenditure of energy will actually increase the total entropy of the entire cumulative system by a greater amount than the “ordering” process decreases it. As a result, the total entropy always goes up.

From another, equivalent perspective, the total amount of information in a physical system can only stay the same or increase; it can never go down.

But for black holes, there’s a paradox which arises, as this “information preservation, or increase” doesn’t appear to necessarily be the case. If you throw a book into a black hole, that book contains all sorts of information: the order of the pages, the text contained on them, the quantum properties (like baryon number and lepton number) of the particles making up the pages and the cover, etc. That information goes into the black hole, adding to its mass/energy and increasing the size and surface area of the black hole’s event horizon. Much later, when the black hole decays via Hawking radiation, that energy comes back out, but the information encoded in that radiation is predicted to be totally random: it’s as though the book’s information has been erased. Despite ongoing claims that this paradox, the information paradox, has come to an end, it still remains very much unsolved. Here’s the science of what’s really going on.

An artist's illustration of a supermassive black hole with an accretion disk and relativistic jets. — Credit: Big Think / NASA

Every particle and system of particles that exists within this Universe has a certain amount of information inherent to it. Some of those properties are static: things like mass, charge, the number of baryons (protons and neutrons) and leptons (electrons) present, magnetic moment, etc. But other properties are dependent on the system that it’s a part of, as well as the history of its interactions: things like its quantum entanglement properties, its spin and orbital angular momentum, and whether there are any bindings between quantum particles. If we could know the exact microstate of a system — the quantum state of every particle included within it, at any moment in time — we’d know everything that was knowable about it.

Of course, in reality, that’s neither physically nor practically possible. We have properties that we do know and can measure, like the temperature of a gas, and then things we not only don’t know, but can’t know due to the fundamental nature of quantum uncertainty: like the positions and momenta of every atom within that gas. Instead of thinking of entropy as a measure of disorder, which is misleading and incomplete, it’s more accurate to think of entropy as the amount of “missing information” needed to determine your system’s specific microstate. That definition of entropy, to think of it as the missing information that keeps you from knowing everything you’d ever possibly want to know, is key to making sense of the idea of quantum information.

maxwell demon — Credit: Htkym/Wikimedia Commons

In our Universe, to the best of our understanding, the entropy of a full physical system, including all “external” influences, inputs, and outputs, can never decrease. The second law of thermodynamics demands that if you:

take any physical system you like,
and you don’t allow anything to enter or leave it (i.e., make sure it’s closed and isolated),
then its entropy can only increase or, at best, stay the same; it can never go down.

A consequence of this is that eggs can’t unscramble themselves, lukewarm water never separates into hot and cold components, and fallen ashes won’t ever spontaneously reassemble into their pre-combustion configuration.

That’s why the black hole information paradox is such a puzzle. If you take something that’s full of information and throw it into a black hole, the black hole gains all of the mass, energy, charge, and angular momentum that entered it. But what happens to the information? In principle, it could get stretched out and encoded onto the surface of the black hole itself. One of the ways we can define a black hole’s entropy is to do it in such a way that its surface area provides a place for every quantum of information to reside, with each “Planck area” of the black hole’s event horizon capable of encoding a single bit (or, possibly, a qubit) of information.

black hole information encoded — Credit: T.B. Bakker/Dr. J.P. van der Schaar, Universiteit van Amsterdam

But even with that additional definition of entropy for black holes, there’s no known way to maintain that information eternally. Eventually, over time, that black hole will spontaneously decay: a consequence of the curvature of spacetime outside the black hole’s event horizon. That curvature is determined by the black hole’s mass, with lower-mass black holes curving space more severely at the event horizon than their larger-mass counterparts.

Whenever spacetime is curved, it has slightly different properties — particularly for its vacuum, or lowest-energy, state — than when it is either less curved or flat-and-uncurved. It’s this difference between vacuum states at different points in the spacetime around a black hole that leads to something profound: the emission of radiation away from the more severely-curved region. Recent research has suggested that this applies to all regions of curved space, not just for the curved space around black holes.

As Stephen Hawking famously demonstrated in 1974, black holes aren’t completely black, as they do emit radiation after all. That radiation:

has a blackbody spectrum: the same properties it would have if you heated a completely black, perfectly absorptive body to a specific finite temperature,
where that temperature is defined by the mass of the black hole,
where each quantum of radiation carries energy, which causes the black hole to lose mass via Einstein’s E = mc²,
in a process that continues, at an accelerating rate (radiating faster as the black hole loses mass) until the black hole evaporates entirely.

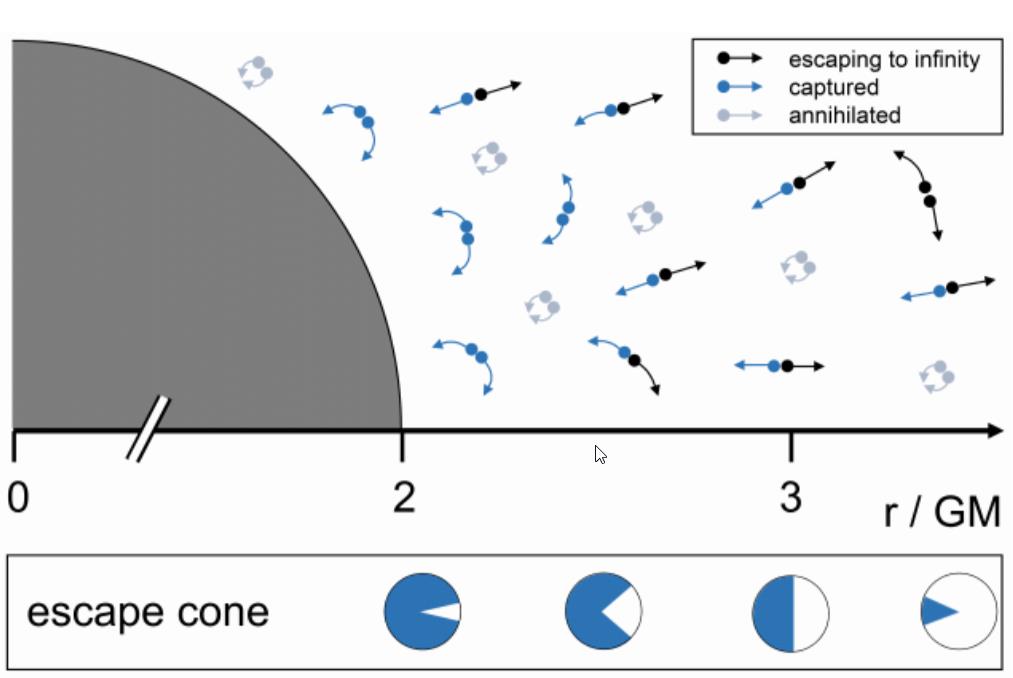
escape fraction relative to a black hole — Credit: M.F. Wondrak et al., Phys. Rev. Lett. accepted, 2023

But you might notice that something is missing: this radiation doesn’t seem to encode, in any way, knowledge of the information that went into the creation of the black hole in the first place. Somewhere along the way, information was destroyed. That’s the key puzzle behind the black hole information paradox. No one seriously disputes the initial setup of the puzzle: that information exists, and that the information (and entropy) does in fact go into the black hole both when it’s first created and also as it grows. What is up for debate, and what in fact is the big question behind the information paradox, is whether that information comes back out again or not.

The way we calculate what comes out of a black hole via Hawking radiation, despite the fact that Hawking radiation has been around for a full half century as of 2024, hasn’t changed all that much over the past 50 years. What we do is assume the curvature of space from general relativity: the fabric of space is curved by the presence of matter and energy, and general relativity tells us exactly by how much.

We then perform our quantum field theory calculations in that curved space, detailing the radiation that comes out as a result. That’s where we learn that the radiation has the temperature, spectrum, entropy, and other properties we know that it possesses, including the fact that it doesn’t appear to encode that initial information when the radiation comes out.

black hole evaporation — Credit: Aurore Simmonet

This is what we call a semi-classical calculation: where we treat the particles and fields in the Universe as quantum, but we don’t quantize spacetime or gravity, and instead use the “classical” background of Einstein’s general relativity to describe the spacetime in which these quantum fields and particles exist. Under this semi-classical approach, as time goes on, the black hole in question loses mass, causing its radiation rate (and temperature, and the entropy of the radiation) to increase, until the black hole is entirely gone.

So, where did all that initial information go, if it doesn’t reappear somehow in the radiation that the black hole evaporates into? Something doesn’t add up about all of this, clearly. But where, exactly, is the flaw? In general, we typically consider three possibilities:

The information loss occurs, but isn’t a problem, due to some process we don’t understand that allows that information loss to occur in a paradox-free fashion.
That even though black holes radiate like we think, information isn’t lost, and is somehow encoded in that radiation, meaning that we’re likely drawing incorrect conclusions based on the assumptions we’ve made.
Or, quite possibly, there’s something wrong with the fundamental assumptions we’ve made in even formulating this paradox, and we don’t understand black hole entropy correctly at all.

Although the proposed solutions aren’t even necessarily limited to these three possibilities, most physicists who work in this area typically expect something interesting is going on with either the second or third possibilities. There’s an excellent reason to think they might be right.

kerr black hole spacetime — Credit: Andrew Hamilton/JILA/University of Colorado

The space outside of a black hole is enormously complicated, even if we treat it as an idealized, rather than a physically realistic, system. While most of us think of space similarly to how Newton did — as an imaginary three-dimensional grid, perhaps with an additional layer of Einsteinian curvature to it — it’s perhaps more accurate to think of the space around a black hole as being like a moving walkway or a river: something that moves and “flows” all on its own. You can walk or swim with, against, or perpendicular to the current, but the important fact is that space behaves as a non-static, in-motion entity all on its own.

In addition to that, we’re assuming that the laws of general relativity are still perfectly accurate for describing the dynamics of space at a quantum level: we are assuming that the quantum effects that create Hawking radiation are important, and they certainly must be. However, we’re also assuming that any quantum effects that arise from treating space as a classical and continuous background (which it may not be) can be ignored. Researchers who work on this call this approach a “semi-classical approximation,” and the suspicion is that something about it, somewhere along the lines, must break down.

But if the semi-classical approximation isn’t a fully correct approach, then what is the correct way to conceive of this problem? How do we successfully perform this calculation, determining the right quantum properties for the exiting Hawking radiation and determining exactly where that incoming information winds up when the black hole has completely decayed away?

Answering those questions successfully would, in fact, provide a solution to the black hole information paradox. It’s important that everyone realize, though, that despite occasional and repeated declarations from prestigious scientists and science outlets, including Quanta, who declared in 2020 that “The Most Famous Paradox in Physics Nears Its End,” those questions have not been answered at all.

What has happened is indeed interesting: a series of papers and calculations have shown that when the black hole nears the end of its life, having shrunk significantly, you can no longer “wall off” the interior of the black hole from the outside. These effects, while negligible in our relatively young Universe, will eventually dominate the dynamics of the evaporating black hole and, consequentially, the radiation that escapes from it. But this advance, like all others that have actually occurred, still doesn’t answer the core puzzle of the black hole information paradox: is information preserved, and if so, how?

black hole hawking — Credit: University of Texas at San Antonio

The 2020 article itself does a good job of diving into many of the details, including a fact that hasn’t been appreciated nearly enough: when radiation comes out of a black hole, it should maintain a quantum mechanically entangled link to the interior of the black hole. That in itself is of supreme importance, as it demonstrates one surefire way that the semi-classical approximation we’ve used ever since the time of Hawking breaks down: entanglement must be taken into account, including across the boundary of the event horizon.

There have also been fascinating — but difficult to put into simple terms — theoretical advances that help map the entropy of the black hole’s interior to the outgoing radiation, providing a suggestion that this might be a fruitful pathway toward understanding how the information gets encoded back into the Universe we can access and experience. At this point, however, we’re only calculating overall properties: like putting masses on a scale and seeing if they balance. We don’t know what happens to the individual quanta and how things like their individual:

masses,
electric and/or color charges,
baryon numbers,
lepton numbers,
magnetic moments,

and so on are going to imprint themselves on that radiation. Baryon number and lepton number are especially puzzling, as Hawking radiation should have a net baryon and lepton number, individually, of zero, irrespective of the initial black hole’s mass, charge, and angular momentum.

The questions of whether:

the information of an evaporating black hole is preserved,
and if so, of how the information gets out,
as well as the question of if that information can actually be physically gathered and measured once again,

all remain as legitimate questions, all without a satisfying answer. The good news is that we’ve made progress on the core issue of the black hole information paradox: we can state with a fair amount of certainty that (at least) one of the assumptions that went into the problem, as initially formulated, is incorrect. We cannot simply look at the space outside of a black hole when we calculate the outgoing radiation; there’s a continuous interplay between that radiation and the interior of the black hole itself. As the black hole evaporates, the interior begins to contain information that’s linked to the outgoing radiation, and thus the black hole’s interior can no longer be ignored.

Unfortunately, we’re still a long way away from determining exactly where that information goes, and how (and whether) it actually gets out of the black hole at all. Theorists disagree over the validity and soundness of many of the methods that are currently being employed to do these calculations, and no one has even a theoretical prediction for how this information should be encoded by an evaporating black hole, much less how to measure it. The black hole information paradox will no doubt be making headlines numerous times over the coming years as developments continue, but a sufficient solution to the big question — of where does the information go — is arguably as far away as ever.