Walk Like an Eulerian: the Bridges of Königsberg

Leonhard Euler (1707-1783) was one of the world’s most important mathematicians, and certainly is a candidate for the most prolific: in 1775 alone, he wrote an average of one mathematical paper per week. During his lifetime, he published more than 500 books and papers. His collected works would fill up to 80 quarto volumes.

Euler made important contributions to fields as diverse as optics, graph theory, fluid dynamics and astronomy. The list of functions, theorems, equations and numbers named after Euler is so long that some joke that they really should be named after the first person after Euler to discover them (1).

An apocryphal tale has Euler, a devout Christian, silencing the free-thinking French philosopher Diderot with a mathematical formula proving the existence of God (2). But perhaps Euler’s best-remembered contribution to science is his solution to the so-called Problem of the Seven Bridges of Königsberg. Maybe because it involves an easily graspable map, rather than abstruse algebraic formulae.

The Prussian city of Königsberg (3) spanned both banks of the river Pregel, which washes around the Kneiphof, a small island at the centre of town, and a larger island immediately to its east. Seven bridges connected both banks and both islands with each other. A popular pastime among the citizens of Königsberg was to attempt a solution to a seemingly intractable problem: How to walk across both banks and both islands by crossing each of the seven bridges only once. The names of the bridges, west to east and north to south, are:

Hohe Brücke to the south of the Fähre (ferry), outside of this map. For complete map of Königsberg in 1905, see here.

In 1735, Euler reformulated the riddle in abstract terms – and once and for all proved that the Königsberg Bridge Problem was indeed unsolvable. Euler recast the actual location as an set of nodes (vertices) connected by links (edges). The exact layout of the terrain did not matter, as long as the nodes remained linked in the original way. He then solved the problem analytically rather than by exhaustively listing all possible permutations:

“My whole method relies on the particularly convenient way in which the crossing of a bridge can be represented. For this I use the capital letters A, B C, D, for each of the land areas separated by the river. If a traveler goes from A to B over bridge a or b, I write this as AB, where the first letter refers to the area the traveler is leaving, and the second refers to the area he arrives at after crossing the bridge. Thus, if the traveler leaves B and crosses into D over bridge f, this crossing is represented by BD, and the two crossings AB and BD combined I shall denote by the three letters ABD, where the middle letter B refers to both the area which is entered in the first crossing and to the one which is left in the second crossing.”

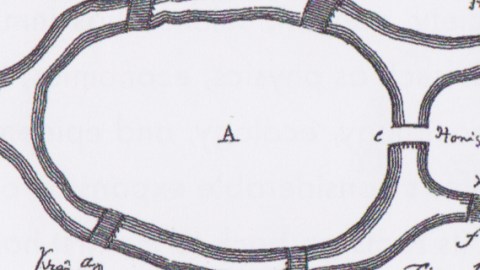
Map from Euler’s paper on the problem. Note the bridge names do not match those on the above map.

Euler proved that the Bridges Problem could only be solved if the entire graph has either zero or two nodes with odd-numbered connections, and if the path (4) starts at one of these odd-numbered connections, and ends at another one. Königsberg has four nodes of odd degree, and thus cannot have an Eulerian Path.

Euler’s analytical solution to the Königsberg Problem is seen as the first theorem of graph theory, an important stage in the development of topography, and a founding text of network science.

Sadly, the original topography for this Problem is all but gone. Those attempting a mathematical pilgrimage to Kaliningrad’s Seven Bridges will be sorely disappointed. Two bridges were destroyed by bombing at the end of the Second World War, two more were demolished and replaced by a Soviet highway. Of the other three originals, one other had been rebuilt in 1935. So of the remaining five, only two date from Euler’s time. 

Does the newer, Soviet configuration make it possible to cross all bridges only once? Darn it, we should have paid more attention in math class. For a more extensive treatment of Euler’s paper, including the conclusion that should be able to solve the newer riddle as well, see this document at the Mathematical Association of America.

Google Maps showing the Knaypkhof today, including the grave of Immanuel Kant. 

Unless mentioned otherwise, the images for this post were taken from Visual Complexity: Mapping Patterns of Information, by Manuel Lima. The book discusses and demonstrates the visualisation of networks, largely a modern field, again with Euler as one of its earliest pioneers.

Strange Maps #536

Got a strange map? Let me know at [email protected].

(1) An impressively long list here. Not included are Euler’s so-called carrés magiques, 81-square grid puzzles that some consider to be early versions of sudoku. 

(2) Pour la petite histoire: (a+b^n)/n=x – although Euler mainly proved that Diderot didn’t know enough about algebra to reply in kind.

(3) Presently the Russian city of Kaliningrad, enclaved between Poland and Lithuania.

(4) Such routes are called Euler Walks or Eulerian Paths in the mathematician’s honour.