This map of Europe is good for only one thing

Euler’s seven-bridge problem: the origin point for topology, and now also a board game.Credit: Puzzling Pixel Games

Here’s an ology you might not have heard of, despite its deceptively familiar-sounding name: topology. And if you have, well done you. But even then, you’ve probably never considered its cartographic implications.

Topology is the mathematical study of the properties that objects preserve even as they are deformed, twisted and stretched – but not broken or glued together. Because of all that twisting and stretching, topology is also often called ‘rubber-sheet geometry’.

For example, since a circle can be stretched to an ellipse, this means that both objects are topologically equivalent. The same applies in three-dimensional space: a sphere can be stretched into an ellipsoid, so both are topologically equivalent.

To clarify further, a counterexample: a figure 8 cannot be deformed into a circle without ‘breaking’ it, so both objects are not topologically equivalent.

The theoretical malleability from one object to another that topology presupposes is at the basis of the first topology joke you’ve ever heard, and the last one you’ll ever need.

Q: What is a topologist?

A: Someone who can’t distinguish between a donut and a coffee mug.

(tumbleweeds)

Now it’s a coffee mug, now it’s a donut. To a topologist, they’re the same anyway.Credit: Lucas Vieira, public domain.

All this seems a bit pointless, so what is topology actually for? The point of it is that some geometric problems depend not on the shape of the objects involved, but on the way they’re put together.

This issue first came up in the mid-18th century, in Leonhard Euler’s so-called ‘seven-bridge problem’ (see also #536). Euler proved you could not go around Königsberg by using all of its bridges just once – but this had nothing to do with their inherent properties; only with how they were placed.

Despite being a relatively young branch of mathematics–topology only really took off in the early 20th century–it has already sprouted several branches of its own, including general, algebraic, and differential topology.

Topology also has a wide variety of applications: it informs the study of biological nanostructures, it’s relevant for computer programming, it serves as a tool for string theorists, and it’s even used to describe the very shape of the universe (in what is called spacetime topology).

Washington DC’s Metro Map, designed on the same topological principle as most other metro maps the world over.Credit: Montrealais, CC BY-SA 3.0

Fortunately, the intersection of topology and cartography involves a lot less rocket science. Simply put, a topological map is a diagram from which unnecessary detail has been removed so that only the relationship between the various points is shown.

Perhaps the most famous example is the schematic map of the London Underground, which represents the network of Tube stations with the simplicity of an electrical grid, ignoring actual distance and routes between the stations, showing only how they interconnect. (See also #119). That representation has now become global standard for metro maps.

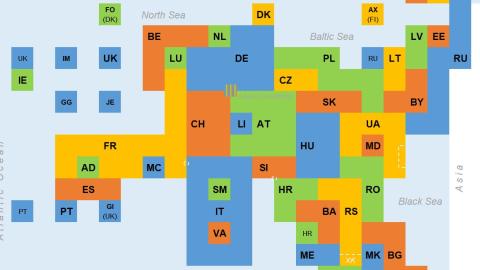
Peter Staub is a spatial data engineer and map geek who has taken topology above ground. He recently produced this Topologist’s Map of Europe, and it’s a delight.

The outline of Europe is still vaguely recognisable, but most of the the countries are bent and twisted right out of shape. Credit: © Peter Staub, Mollis GL/Switzerland – CC BY SA

As per the definition above, this topological map is a diagram from which all details have been removed, except the spatial relationship between the various countries. So we see exactly which other countries they border. To show those relationships, the countries’ actual shapes and sizes have been totally sacrificed.

Take Italy, for example: boot-shaped on any normal map, here the country looks like the figure 8, to accommodate the two countries enclaved inside of it: the Vatican and San Marino.

Poland still borders Germany, the Czech Republic, Slovakia, Ukraine, Belarus, Lithuania and the Russian exclave of Kaliningrad, as it does in real life; but to do so, the country has had to change from a block into a squiggle.

France now looks like a long-bottomed chair with Andorra and Monaco between its legs, and Belgium for a headrest.

Countries are denoted by their internet TLDs (Top-Level Domain names). Some of the less familiar ones are Isle of Man (IM), Jersey (JE), and Guernsey (GG) – all dependencies of the British Crown.

The map also painstakingly reflects Europe’s most controversial territorial disputes, hence the dotted lines across Cyprus (for the almost universally unrecognised breakaway republic of Northern Cyprus) and in Ukraine (supposedly for Russia’s unilateral annexation of Crimea – or are these the breakaway areas in the east controlled by pro-Russian rebels?)

The weirdness that is Lake Constance – topologically speaking.Credit: © Peter Staub, Mollis GL/Switzerland – CC BY SA

Small dotted areas indicate disputes between Slovenia and Croatia, and between France and Italy (about whether the border between them crosses the summit of Mont Blanc or not).

Kosovo is recognised by many countries, but not yet by Serbia, from which it broke away. It doesn’t get its own block, but its TLD (XK) is mentioned below the dotted line.

And what about that little area in between Germany (DE), Switzerland (CH), and Austria (AT) that looks like there’s something wrong with your television? That’s Lake Constance, on the border between Germany, Switzerland, and Austria. According to Switzerland, the border runs right down the middle of the lake. Austria claims the entire lake is a condominium between the three countries, and Germany’s position is ambiguous.

As such, Lake Constance is the only area in Europe where neighboring states have never managed to agree on a border. Now, that’s something you wouldn’t have learned if this wasn’t a topological map.

Map found here on Peter Staub’s Twitter, which also contains topology maps of Germany, Switzerland and the Americas.

Strange Maps #1073

Got a strange map? Let me know at [email protected].

Follow Strange Maps on Twitter and on Facebook.