Why You Should Doubt ‘New Physics’ From The Latest Muon g-2 Results

The mismatch between theory and experiment is anything but certain.

The most exciting moments in a scientist’s life occur when you get a result that defies your expectations. Whether you’re a theorist that derives a result that conflicts with what’s experimentally or observationally known, or an experimentalist or observer who makes a measurement that gives a contrary result to your theoretical predictions, these “Eureka!” moments can go one of two ways. Either they’re harbingers of a scientific revolution, exposing a crack in the foundations of what we had previously thought, or — to the chagrin of many — they simply result from an error.

The latter, unfortunately, has been the fate of every experimental anomaly discovered in particle physics since the discovery of the Higgs boson a decade ago. There’s a significance threshold we’ve developed to prevent us from fooling ourselves: 5-sigma, corresponding to only a 1-in-3.5 million chance that whatever new thing we think we’ve seen is a fluke. The first results from Fermilab’s Muon g-2 experiment have just come out, and they rise to a 4.2-sigma significance: compelling, but not definitive. But it’s not time to give up on the Standard Model just yet. Despite the suggestion of new physics, there’s another explanation. Let’s look at the full suite of what we know today to find out why.

What is g? Imagine you had a tiny, point-like particle, and that particle had an electric charge to it. Despite the fact that there’s only an electric charge — and not a fundamental magnetic one — that particle is going to have magnetic properties, too. Whenever an electrically charged particle moves, it generates a magnetic field. If that particle either moves around another charged particle or spins on its axis, like an electron orbiting a proton, it will develop what we call a magnetic moment: where it behaves like a magnetic dipole.

Quantum mechanically, point particles don’t actually spin on their axis, but rather behave like they have an intrinsic angular momentum to them: what we call quantum mechanical spin. The first motivation for this came in 1925, where atomic spectra showed two different, very closely-spaced energy states corresponding to opposite spins of the electron. This hyperfine splitting was explained 3 years later, when Dirac successfully wrote down the relativistic quantum mechanical equation describing the electron.

If you only used classical physics, you would’ve expected that the spin magnetic moment of a point particle would just equal one-half multiplied by the ratio of its electric charge to its mass multiplied by its spin angular momentum. But, because of purely quantum effects, it all gets multiplied by a prefactor, which we call “g.” If the Universe were purely quantum mechanical in nature, g would equal 2, exactly, as predicted by Dirac.

What is g-2? As you might have guessed, g doesn’t equal 2 exactly, and that means the Universe isn’t purely quantum mechanical. Instead, not only are the particles that exist in the Universe quantum in nature, but the fields that permeate the Universe — the ones associated with each of the fundamental forces and interactions — are quantum in nature, too. For example, an electron experiencing an electromagnetic force won’t just attract or repel from an interaction with an outside photon, but can exchange arbitrary numbers of particles according to the probabilities you’d calculate in quantum field theory.

When we talk about “g-2,” we’re talking about all the contributions from everything other than the “pure Dirac” part: everything associated with the electromagnetic field, the weak (and Higgs) field, and the contributions from the strong field. In 1948, Julian Schwinger — co-inventor of quantum field theory — calculated the largest contribution to the electron and muon’s “g-2:” the contribution of an exchanged photon between the incoming and outgoing particle. This contribution, which equals the fine-structure constant divided by 2π, was so important that Schwinger had it engraved on his tombstone.

Why would we measure it for a muon? If you know anything about particle physics, you know that electrons are light, charged, and stable. At just 1/1836 the mass of the proton, they’re easy to manipulate and easy to measure. But because the electron is so light, its charge-to-mass ratio is very low, which means the effects of “g-2” are dominated by the electromagnetic force. That’s very well understood, and so even though we’ve measured what “g-2” is for the electron to incredible precision — to 13 significant figures — it lines up with what theory predicts spectacularly. According to Wikipedia (which is correct), the electron’s magnetic moment is “the most accurately verified prediction in the history of physics.”

The muon, on the other hand, might be unstable, but it’s 206 times as massive as the electron. Although this makes its magnetic moment comparatively smaller than the electron’s, it means that other contributions, particularly from the strong nuclear force, are far greater for the muon. Whereas the electron’s magnetic moment shows no mismatch between theory and experiment to better than 1-part-in-a-trillion, effects that would be imperceptible in the electron would show up in muon-containing experiments at about the 1-part-in-a-billion level.

That’s precisely the effect the Muon g-2 experiment is seeking to measure to unprecedented precision.

What was known before the Fermilab experiment? The g-2 experiment had its origin some 20 years ago at Brookhaven. A beam of muons — unstable particles produced by decaying pions, which themselves are made from fixed-target experiments — are fired at very high speeds into a storage ring. Lining the ring are hundreds of probes that measure how much each muon has precessed, which in turn allows us to infer the magnetic moment and, once all the analysis is complete, g-2 for the muon.

The storage ring is filled with electromagnets that bend the muons into a circle at very high, specific speeds, tuned to precisely 99.9416% the speed of light. That’s the specific speed known as the “magic momentum,” where electric effects don’t contribute to precession but magnetic ones do. Before the experimental apparatus was shipped cross-country to Fermilab, it operated at Brookhaven, where the E821 experiment measured g-2 for the muon to 540 parts-per-billion precision.

The theoretical predictions we’d arrived at, meanwhile, differed from Brookhaven’s value by about ~3 standard deviations (3-sigma). Even with the substantial uncertainties, this mismatch spurred the community on to further investigation.

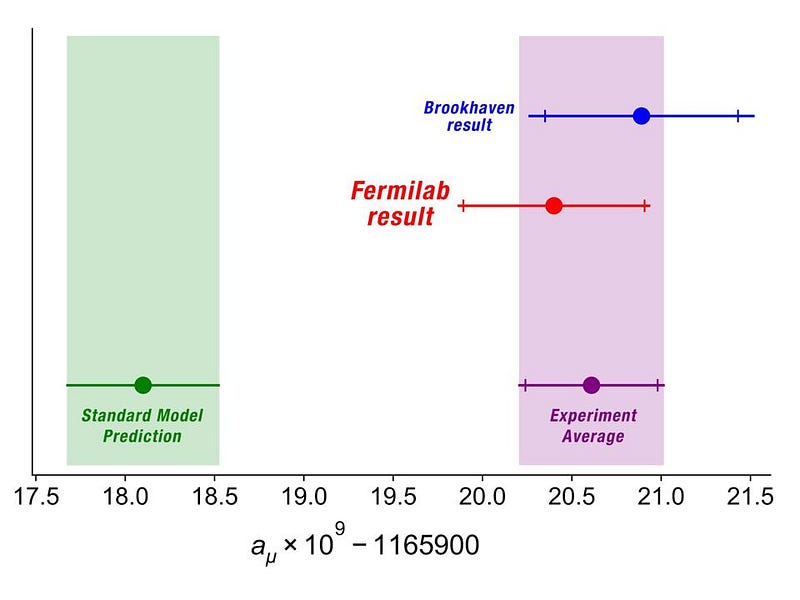
How did the newly-released results change that? Although the Fermilab experiment used the same magnet as the E821 experiment, it represents a unique, independent, and higher-precision check. In any experiment, there are three types of uncertainties that can contribute:

1. statistical uncertainties, where as you take more data, the uncertainty goes down,
2. systematic uncertainties, where these are errors that represent your lack-of-understanding of issues inherent to your experiment,
3. and input uncertainties, where things you don’t measure, but assume from prior studies, have to have their associated uncertainties brought along for the ride.

A few weeks ago, the first set of data from the Muon g-2 experiment was “unblinded,” and then presented to the world on April 7, 2021. This was just the “Run 1” data from the Muon g-2 experiment, with at least 4 total runs planned, but even with that, they were able to measure that “g-2” value to be 0.00116592040, with an uncertainty in the last two digits of ±43 from statistics, ±16 from systematics, and ±03 from input uncertainties. Overall, it agrees with the Brookhaven results, and when the Fermilab and Brookhaven results are combined, it yields a net value of 0.00116592061, with a net uncertainty of just ±35 in the final two digits. Overall, this is 4.2-sigma higher than the Standard Model’s predictions.

Why would this imply the existence of new physics? The Standard Model, in many ways, is our most successful scientific theory of all-time. In practically every instance where it’s made definitive predictions for what the Universe should deliver, the Universe has delivered precisely that. There are a few exceptions — like the existence of massive neutrinos — but beyond that, nothing has crossed the “gold standard” threshold of 5-sigma to herald the arrival of new physics that wasn’t later revealed to be a systematic error. 4.2-sigma is close, but it’s not quite where we need it to be.

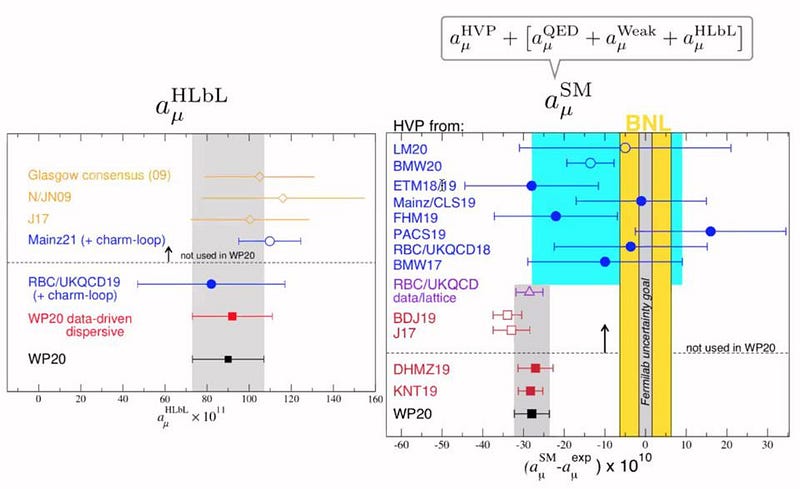
But what we’d want to do in this situation versus what we can do are two different things. Ideally, we’d want to calculate all the possible quantum field theory contributions — what we call “higher loop-order corrections” — that make a difference. This would include from the electromagnetic, weak-and-Higgs, and strong force contributions. We can calculate those first two, but because of the particular properties of the strong nuclear force and the odd behavior of its coupling strength, we don’t calculate these contributions directly. Instead, we estimate them from cross-section ratios in electron-positron collisions: something particle physicists have named “the R-ratio.” There is always the concern, in doing this, that we might suffer from what I think of as the “Google translate effect.” If you translate from one language to another and then back again to the original, you never quite get back the same thing you began with.

The theoretical results we get from using this method are consistent, and keep coming in significantly below the Brookhaven and Fermilab results. If the mismatch is real, this tells us there must be contributions from outside the Standard Model that are present. It would be fantastic, compelling evidence for new physics.

How confident are we of our theoretical calculations? As theorist Aida El-Khadra showed when the first results were presented, these strong force contributions represent the most uncertain component of these calculations. If you accept this R-ratio estimate, you get the quoted mismatch between theory and experiment: 4.2-sigma, where the experimental uncertainties are dominant over the theoretical ones.

While we definitely cannot perform the “loop calculations” for the strong force the same way we perform them for the other forces, there’s another technique that we could potentially leverage: computing the strong force using an approach involving a quantum lattice. Because the strong force relies on color, the quantum field theory underlying it is called Quantum Chromodynamics: QCD.

The technique of Lattice QCD, then, represents an independent way to calculate the theoretical value of “g-2” for the muon. Lattice QCD relies on high-performance computing, and has recently become a rival to the R-ratio for how we could potentially compute theoretical estimates for what the Standard Model predicts. What El-Khadra highlighted was a recent calculation showing that certain Lattice QCD contributions do not explain the observed discrepancy.

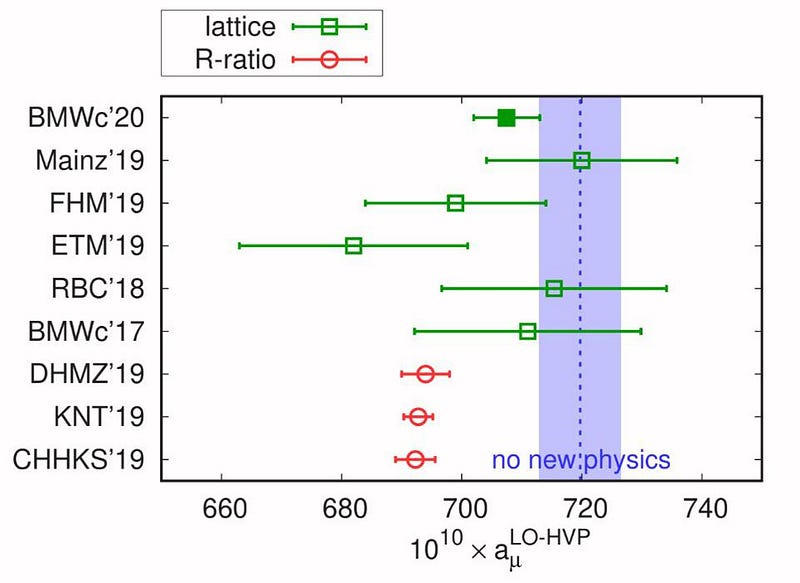
The elephant in the room: lattice QCD. But another group — which calculated what’s known to be the dominant strong-force contribution to the muon’s magnetic moment — found a significant discrepancy. As the above graph shows, the R-ratio method and the Lattice QCD methods disagree, and they disagree at levels that are significantly greater than the uncertainties between them. The advantage of Lattice QCD is that it’s a purely theory-and-simulation-driven approach to the problem, rather than leveraging experimental inputs to derive a secondary theoretical prediction; the disadvantage is that the errors are still quite large.

What’s remarkable, compelling, and troubling, however, is that the latest Lattice QCD results favor the experimentally measured value and not the theoretical R-ratio value. As Zoltan Fodor, leader of the team that did the latest Lattice QCD research, put it, “the prospect of new physics is always enticing, it’s also exciting to see theory and experiment align. It demonstrates the depth of our understanding and opens up new opportunities for exploration.”

While the Muon g-2 team is justifiably celebrating this momentous result, this discrepancy between two different methods of predicting the Standard Model’s expected value — one of which agrees with experiment and one of which does not — needs to be resolved before any conclusions about “new physics” can responsibly be drawn.

So, what comes next? A lot of truly excellent science, that’s what. On the theoretical front, not only will the R-ratio and Lattice QCD teams continue to refine and improve their calculational results, but they’ll attempt to understand the origin of the mismatch between these two approaches. Other mismatches between the Standard Model and experiments — although none of them have crossed the “gold standard” threshold for significance just yet — presently exist, and some scenarios that could explain these phenomena could also explain the muon’s anomalous magnetic moment; they will likely be explored in-depth.

But the most exciting thing in the pipeline is better, more improved data from the Muon g-2 collaboration. Runs 1, 2, and 3 are already complete (Run 4 is in progress), and in about a year we can expect the combined analysis of those first three runs — which should almost quadruple the data, and hence, halve the statistical uncertainties — to be published. Additionally, Chris Polly announced that the systematic uncertainties will improve by almost 50%. If the R-ratio results hold, we’ll have a chance to hit 5-sigma significance just next year.

The Standard Model is teetering, but still holds for now. The experimental results are phenomenal, but until we understand the theoretical predictions without this present ambiguity, the most scientifically responsible course is to remain skeptical.

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.