Time: Yes, it’s a dimension, but no, it’s not like space
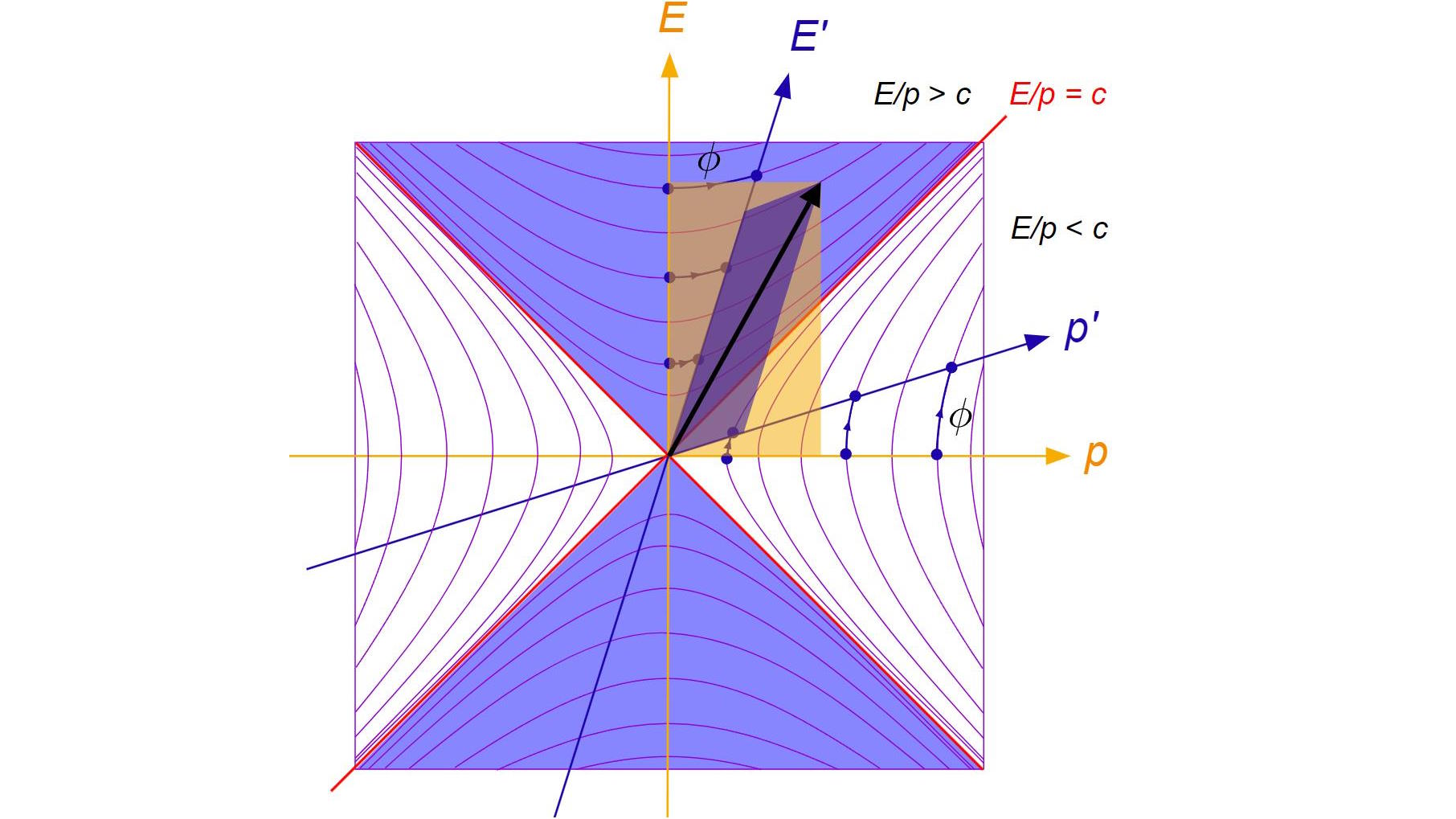
- According to Einstein’s relativity, time and space aren’t absolute quantities that all observers agree upon, but rather they’re experienced differently, and relatively, dependent on spacetime’s curvature and the observer’s motion.
- Even in general relativity, our three spatial dimensions and one time dimension are intertwined, and when you decompose them, stark differences between space’s and time’s behaviors appear.
- Although the mathematics governing them both is straightforward, there are some important ways that time is fundamentally different from space. Yes, it’s a dimension, but it isn’t like the others.
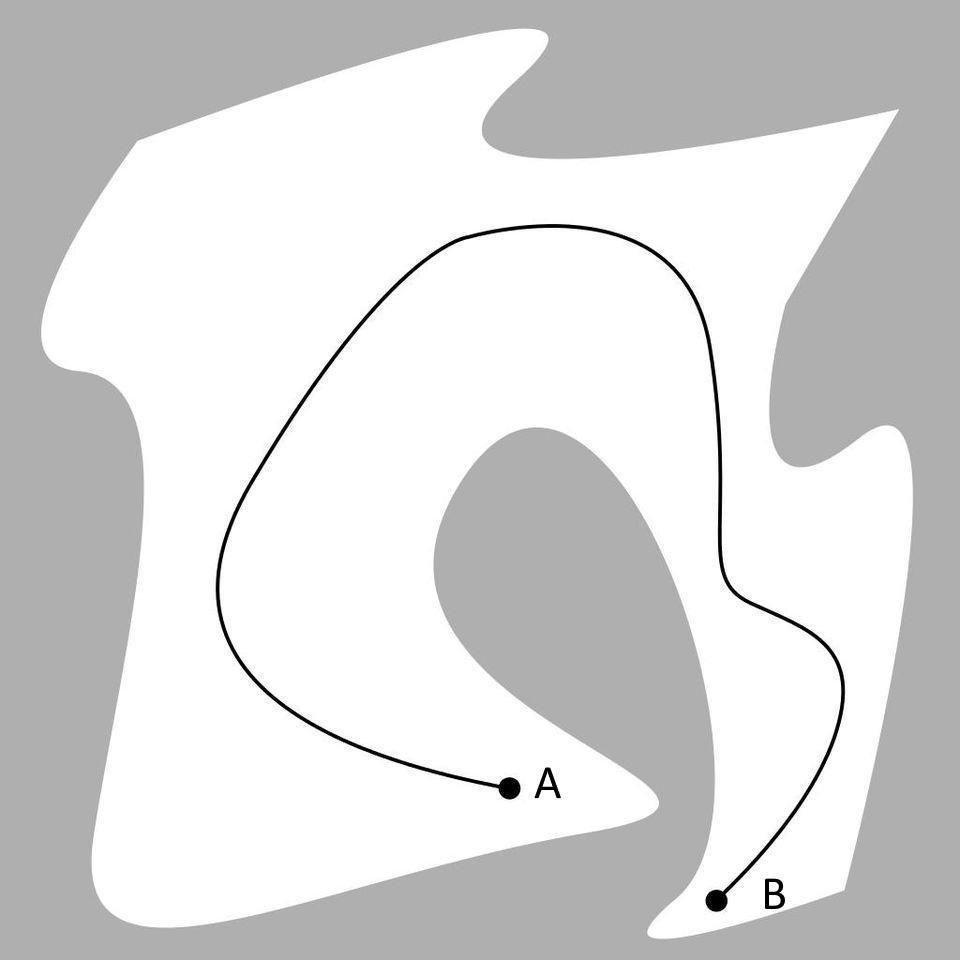
When it comes to dimensions, most of us intuitively understand the notion that space possesses those properties. You can move forward or backward by any amount you desire in any of the three dimensions — up-down, left-right, or forward-backward — in which motion is possible. It’s why, if you ask yourself to draw a path that describes the shortest distance between any two points, most of us will give the same answer that Archimedes gave more than 2,000 years ago: a straight line. If you take a flat sheet of paper and put two points down on it absolutely anywhere, you can connect those two points with any line, curve, or geometrical path you can imagine. So long as the paper remains flat, uncurved, and unbent in any way, the straight line connecting those two points will ultimately represent the shortest path possible.
This intuitive answer correctly describes how the three dimensions of space work in our Universe: in flat space, the shortest distance between any two points is a straight line. This is true regardless of how you rotate, orient, or otherwise position those two points. However, our Universe doesn’t simply possess the three familiar dimensions of space, but rather four spacetime dimensions. It’s easy to look at that and say, “Oh, well, three of them are space and one of them is time, and that’s where we get spacetime,” and that’s true, but not the full story. After all, the shortest distance between two spacetime events isn’t a straight line at all, and moreover, time is a fundamentally different type of dimension than space. Here’s how it actually works.
When did you first realize that the shortest distance connecting any two points in space is going to be a straight line? Most of us learn it as children: cutting across a grassy area to meet a friend or family member, rather than staying on the (often right-angled) paths or sidewalks that would require more time and more steps to traverse. In fact, that realization, as far as human knowledge is concerned, comes from a place we might not realize: the Pythagorean theorem. You might remember the Pythagorean theorem as a rule about right triangles, as it notes that if you square each of the short sides of a right triangle (a and b) and add them together, that equals the square of the long side (c). Mathematically, if we call the short sides “a” and “b” and we call the long side “c,” then the equation relating them is a² + b² = c².
Think about what this means, however: not from the perspective of pure mathematics alone, but in terms of distances. It means that if you move through one of your spatial dimensions by a certain amount (a, for example) and then move through a different, perpendicular dimension by another amount (b, for instance), then the distance between where you began and where you wound up is equal to c, as defined by the Pythagorean theorem. In other words, the distance between any two points on a plane, where those points are separated by a in one dimension and b in a second, perpendicular dimension, will be described by c, where c = √(a² + b²).
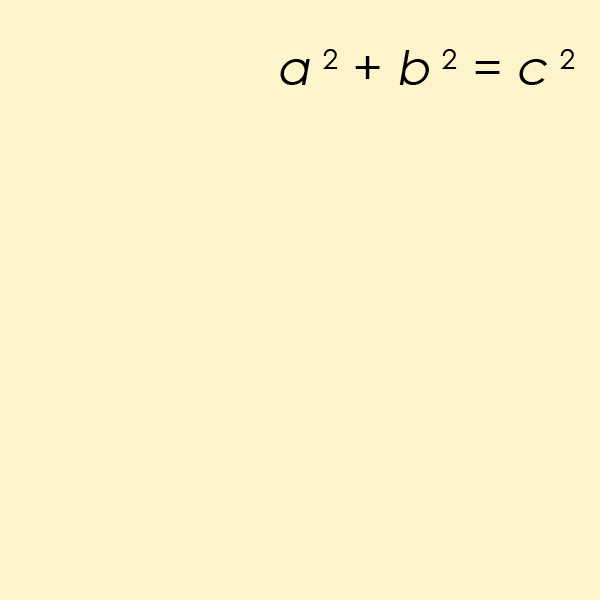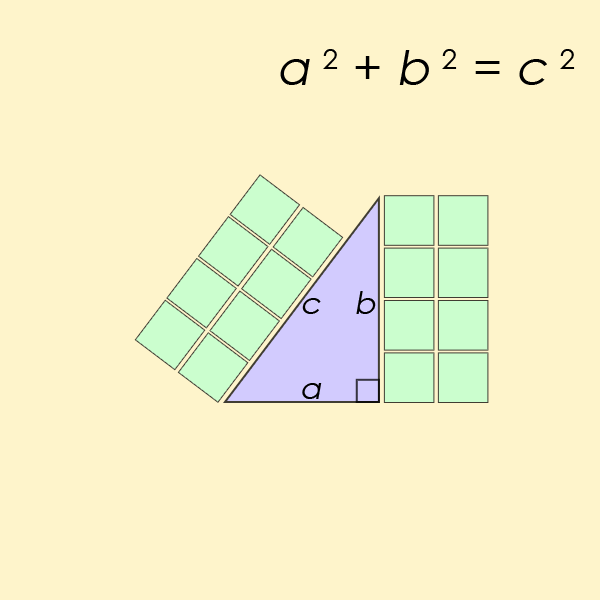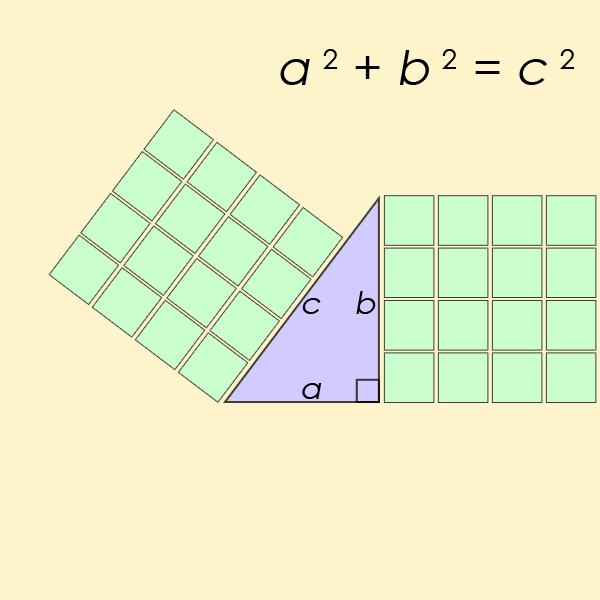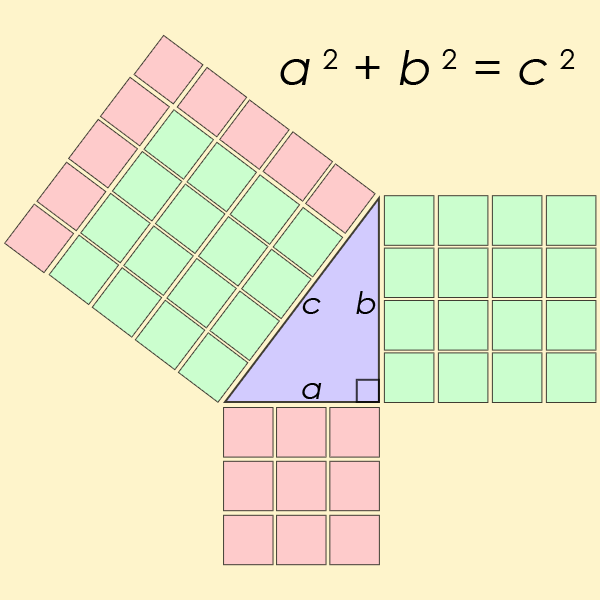
That’s all well and good in flat, grid-like, absolute space: where everyone at all locations, at all times, and irrespective of motion all agrees on the same coordinate system. In our Universe, of course, many of these things aren’t universally true. For example, we’re not restricted to living in flat space, such as a flat sheet of paper. (We live on a spheroidal Earth, for instance.) We have not just length and width (or the x and y directions, if you prefer) dimensions to our Universe, but depth (or the z direction) as well.
Taking all three of these dimensions into account — so long as we assume that space is still flat and universal — how would we then figure out what the distance is between any two points in space? Perhaps surprisingly, we’d use the exact same method as we used in two dimensions, except with one extra dimension thrown in. If you can measure or know the amount your two points are separated by in those three independent, mutually perpendicular dimensions:
- the x direction,
- the y direction,
- and the z direction,
you can figure out the total distance between them by using the same method as earlier. The only difference is, because of the extra dimension, the distance between them — let’s call it d — is going to be given by d = √(x² + y² + z²). This might look like a scary equation, but it just says that the distance between any two points is defined by the straight line connecting them: the line that accounts for the separation between your two points in all three dimensions: the x-direction, the y-direction, and the z-direction combined.
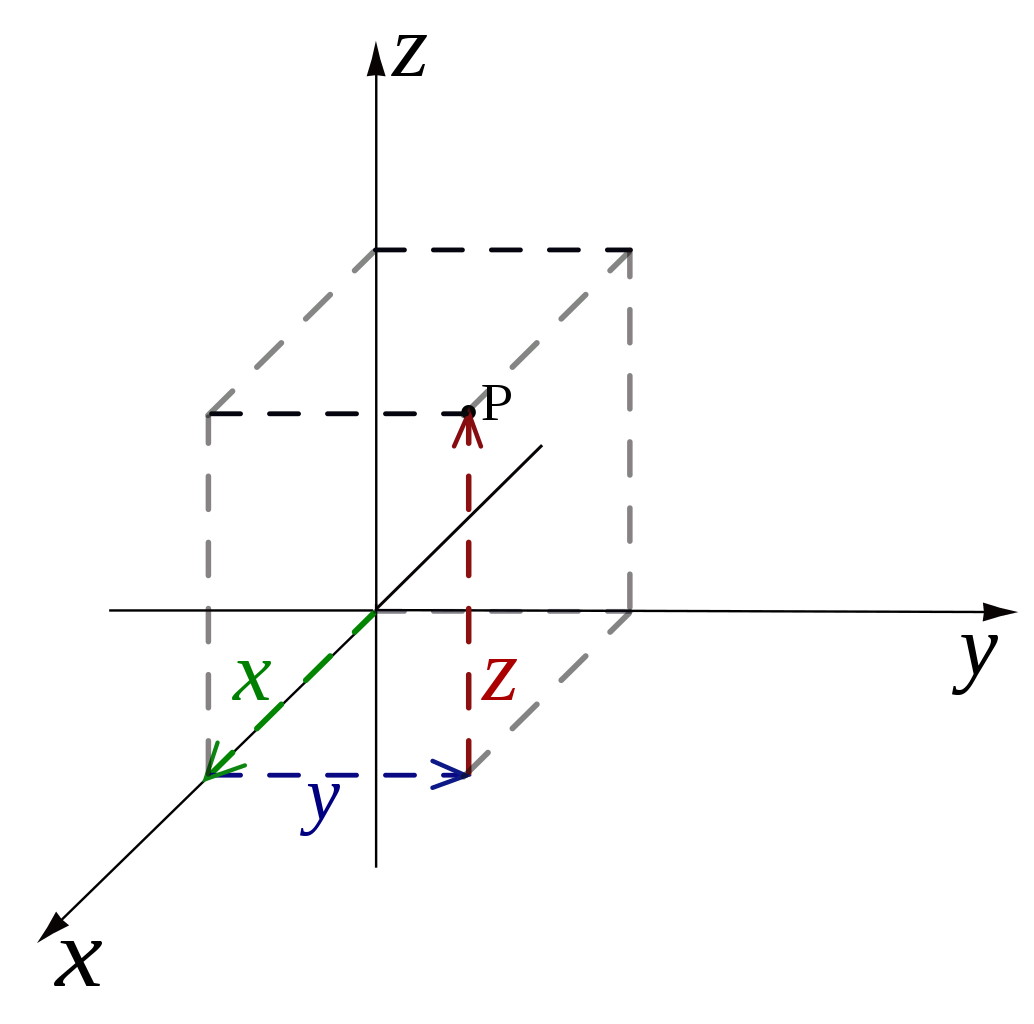
As long as you can draw a three-dimensional spatial grid, where the intersecting grid lines are mutually perpendicular to one another, the distance between any two points within that grid (or within this three-dimensional space) will be given by that same relationship: d = √(x² + y² + z²). The distance between two points being defined by a straight line has some profound implications for that coordinate system (or grid) that you laid down. First off, it absolutely does not matter how you orient your visualization of the x, y, and z dimensions. You are free to:
- change your coordinates by rotating or switching your axes,
- to rotate these two points by any amount about any axis,
- or to orient your x, y, and z dimensions in any (mutually perpendicular) directions at all,
and the distance between those two points, as well as the distance given by d = √(x² + y² + z²), will not change at all.
Sure, the individual components that go into the overall distance (i.e., the values of x, y, and z, individually) will change if you rotate your perspective or rotate the imaginary line connecting your two points, as your definitions of length, width, and depth will change relative to one another. However, the overall distance between those two points won’t change at all; that specific quantity — the distance between those points — remains what we call “invariant,” or unchanging, regardless of how you change your coordinate system.

Thinking about distances like we just did provides a great description of what we’ll wind up with if we consider flat, uncurved space on its own. What will happen when we fold time, as a dimension, into the equation as well? You might think, “Well, if time is just a dimension, too, then the distance between any two points in spacetime will work the same way.” For example, if we represent the time dimension as t, you might think the distance between any two points would be the straight line connecting them in the exact same way: through the three spatial dimensions as well as the time dimension. In mathematical terms, you might think that the equation for the separation between any two points would look something like d = √(x² + y² + z² + t²).
After all, this is pretty much the same change we made when we went from two spatial dimensions to three spatial dimensions, except this time we’re going from three dimensions to four dimensions. It’s a reasonable step to attempt, and describes exactly what reality would look like if we had four dimensions of space, rather than three of space and one of time.
But that actually makes for a huge difference. Instead of four dimensions of space, the fact that we have three dimensions of space and one dimension of time requires us to look at the puzzle differently. Despite what your intuition may have told you, time isn’t “just another dimension” the way spatial dimensions are familiar dimensions.

There are two fundamental ways that time, as a dimension, is different from your typical spatial dimension. The first way is a small but straightforward difference: you can’t put space (which is a measurement of distance, with units like feet or meters) and time (which is a measurement of, well, time, with units like seconds or years) on the same footing as each other right from the start. You have to have some way to convert one of them onto the same footing as the other, otherwise you would be attempting to link together two fundamentally different types of quantity. (You would be very upset if you asked me the distance from New York to Los Angeles and I told you it was 13 milliseconds.)
Fortunately, one of the great revelations of Einstein’s theory of relativity was that there is an important, fundamental connection between distance and time: the speed of light. Any particle or phenomenon that travels through the Universe without a rest mass moves at this speed, including photons, gluons, and gravitational waves.
The speed of light in a vacuum — 299,792,458 meters per second — tells us precisely how to relate our motion through space with our motion through time: by that fundamental constant itself. When we use terms like “one light-year” or “one light-second,” we’re talking about distances in terms of time: the amount of distance that light travels in one year (or one second), for example. (13 milliseconds is the amount of time a photon would take to traverse the New York-Los Angeles distance.) If we want to convert “time” into a distance, the way to accomplish that is to multiply your duration by the speed of light in a vacuum.

However, there’s also a second way that time is fundamentally different from space, as a dimension, and this second difference requires an enormous leap to understand. In fact, it’s a difference that eluded many of the greatest minds of the late 19th and early 20th centuries. The key idea is that all observers, objects, quanta, and other entities that populate our Universe all actually move through the fabric of the Universe — through both space and time — simultaneously. Even if you think of yourself as being at rest, by simply sitting where you are, stationary, and not moving through space at all, it turns out that you’re still moving through time while you’re motionless through space. Moreover, there’s a very specific rate for the passage of time that we’re all familiar with: time passes at the rate of one second per second.
However — and this is the key point — motion through space isn’t just possible, but occurs all the time. It turns out that the faster (and the greater the amount) you move through space, the slower (and the lesser the amount) you move through time. No other dimension has this property; the spatial dimensions are not like this at all. Your motion through the x dimension in space, for example, is completely independent of your motion through the other two (y and z) spatial dimensions. However, it’s your total, cumulative motion through space, as measured relative to any other observer, that determines your motion through time. The more you move through one of them (either space or time), the less you move through the other, complementary quantity.
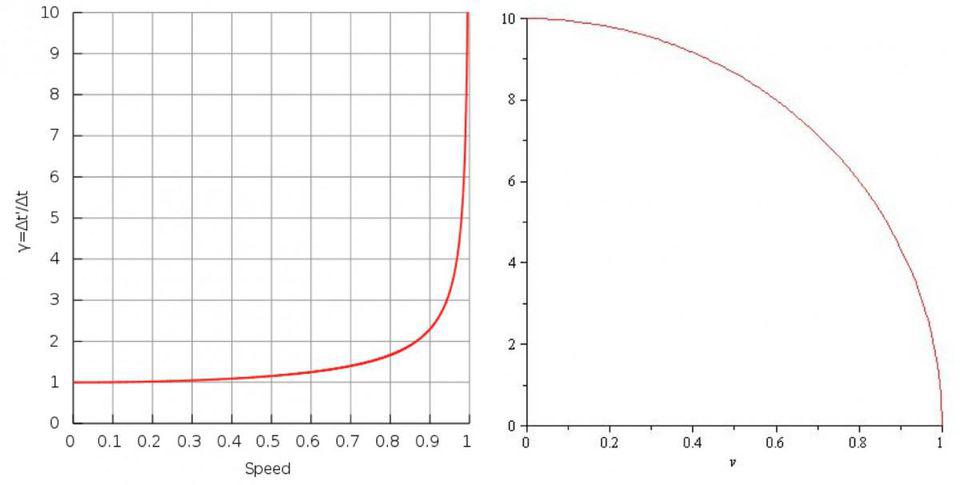
This is the underlying reason why, when you move at speeds that approach the speed of light, you start to experience phenomena such as time dilation and length contraction: aspects of reality that are essential to Einstein’s relativity. If you only move at very low speeds compared to the speed of light, it’s very difficult to notice these effects; time appears to move at one second per second for everyone, and lengths appear to be the same distance for everyone at speeds normally achievable on Earth.
But as you approach the speed of light — or rather, as you perceive an object where the relative speed between you and it is some significant fraction of the speed of light — you’ll observe that the object that you see as “in motion” relative to you:
- appears to have its length contracted along its direction of relative motion,
- has time, or clocks on board it, appear to run at a slower (dilated) rate,
relative to your own clocks and your own ruler or other distance-measuring devices. The reason behind these phenomena, as first realized by Einstein, was straightforward: it’s because the speed of light is a truly, universally invariant quantity. In other words, the speed of light in a vacuum is identical for all observers. If you imagine that a clock is defined by light bouncing back and forth between two mirrors, then watching someone else’s clock as they move close to the speed of light will inevitably result in their clock running slower than your own, even though you both perceive “time” as running at that one-second-per-second rate from your individual frames of reference.

There’s an even deeper insight to be gleaned from these thoughts, which initially eluded even Einstein himself. If you treat time as a dimension, multiply it by the speed of light, and — here’s the big leap — treat it as though it were an imaginary mathematical quantity, rather than a real one, then we can indeed define a “spacetime interval” in much the same fashion that we defined a distance interval earlier: d = √(x² + y² + z²). Instead of adding in a “+ t²” to the equation to define a four-dimensional spacetime interval, as opposed to the three-dimensional idea of distance, we can fold in the conversion factor (the speed of light) and treat time as needing the imaginary number i as a prefactor in the equation.
Since the imaginary number i is just √(-1) and the speed of light is just c, this means that the spacetime interval is actually d = √(x² + y² + z² – c²t²). [Note the minus sign attached to the time coordinate, which comes from squaring the imaginary number i!] In other words, the transformation from “motion through or separation in space” to “motion through or separation in both space and time” is also a rotation, but it’s a rotation not in the cartesian coordinates of space (where x, y, and z are all real numbers), but through the hyperbolic coordinates of spacetime, where if the space coordinates are treated as real quantities, then the time coordinate must be treated as an imaginary one.
In a great twist of fate, the person who first put these puzzle pieces together was Einstein’s former teacher, Hermann Minkowski, who noted in 1907/8 that,
“Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
With Minkowski’s mathematical rigor behind it, the concept of spacetime was not only born, but was here to stay.
What’s remarkable about all of this is that Einstein, despite lacking the mathematical insight to understand exactly how the dimension of time was related to the three conventional dimensions of space, was still able to piece together this key physical insight. Increasing your motion through space decreased your motion through time, and increasing your motion through time decreased your motion through space. All measurements of space and time are only meaningful relative to the observer in question, and depend on the relative motion of the observer to the observed.
And yet, through any transformation you can fathom, the spacetime interval will still remain an invariant quantity. No matter who is doing the observing or how quickly they’re moving, the combined motion of any object through spacetime is something all observers can agree on. In some ways, the success of relativity was made all the more impressive in light of Minkowski’s harsh assessment of Einstein from his recollection of Einstein as a student. Speaking to his (even later) student, Max Born, Minkowski had the following to say,
“For me [relativity] came as a tremendous surprise, for in his student days Einstein had been a real lazybones. He never bothered about mathematics at all.”
Regardless of mathematical ability, the physical insights that:
- the speed of light is a constant for all observers,
- and the only truly invariant quantity is neither distance nor duration, but the spacetime interval,
were the profound foundation that not only led to Einstein’s special and general theories of relativity, and led to our modern understanding of time not only as a dimension, but as a unique type of dimension in our modern, four-dimensional conception of spacetime.