Ask Ethan: Does time exist, or is it an illusion?

One of the most important aspects of physics, or of any science in general, is to always muster up the greatest challenge to the leading physical theories you can. You can challenge prior results, you can challenge the methods used to obtain them, you can concoct new tests in new regimes of potential applicability, and you can even challenge the assumptions underlying them. When it comes to our understanding of the Universe, we believe that we inhabit a four-dimensional “fabric” known as spacetime, with three spatial dimensions and one time dimension, all of which are inextricably woven together.

All of this assumes, of course, that time itself is a real thing: physically real, and fundamental in nature. But are these assumptions necessarily true? Is there any way possible around them, and could time instead be merely an illusion, albeit a convincing one? That’s what Dave Drews wants to know, as he writes in to ask:

“We’ve all heard the philosophical question, ‘If a tree falls in a forest and no one is around to hear it, does it make a sound?’ Some people think time is an illusion, a construct of human minds and experience. If that’s true, then if there were no sentient beings around to experience it, does time exist?”

This is a tough question, and we have many ways to approach it. Let’s try to be as comprehensive as possible, addressing that key question: does time exist?

An example of a light cone, the three-dimensional surface of all possible light rays arriving at and departing from a point in spacetime. The more you move through space, the less you move through time, and vice versa. Only things contained within your past light-cone can affect you today; only things contained within your future light-cone can be perceived by you in the future. This illustrates flat Minkowski space, rather than the curved space of general relativity.

The nature of time

We once thought, as recently as the early 20th century, that time was the same for everyone. That no matter where you were, how fast you were moving, or when you measured it, everyone, everywhere, at all times would agree on what time was: that we would measure its rate of passage to be the same, identically, for everyone. But while we can:

• measure it,
• quantify it,
• observe its passing,
• and observe and measure the consequences of its passage,

it turns out that answering the seemingly simple question of “how much time has passed” between any two events isn’t identical for everyone, after all.

What Einstein taught us is that answering that question, between say the start and end of any event, is very dependent on both where you are and how you’re moving when those observations are conducted. For example, if you’re on a moving train and you shoot a light wave from one end of the train to the other (or up to the ceiling and then down to the floor), you’ll get a specific value for how long it takes the light to reach the other end of the train. If you’re on a platform, however, watching the person on the train shoot the light from one end to the other, you’ll get a different answer from the observer who’s moving on the train along with the light.

A “light clock” will appear to run differently for observers moving at different relative speeds, but this is due to the constancy of the speed of light. Einstein’s law of special relativity governs how these time and distance transformations take place between different observers. However, each individual observer will see time pass at the same rate as long as they remain in their own reference frame: one second-per-second, even though when they bring their clocks together after the experiment, they’ll find that they no longer agree.

For the person on the moving train, they’ll measure that a certain amount of time must elapse for the light to travel down to the far end of the train. But for the person on the ground, they’ll not only get a different, longer answer, but they’ll conclude that the person (and, for that matter, everything) on the train is actually aging more slowly than they are. To the stationary observer, an object in motion ages more slowly than an object at rest.

The reason for this phenomenon is that the “absolute” quantity in nature is neither space nor time, but the velocity of light in a vacuum: the maximal rate that something can move through space and time together. It turns out the greater your motion through space, the lesser your motion through time, and vice versa. This means that if you want to maximize your motion through time, you’ll remain absolutely stationary; anyone in relative motion to you will experience a slower passage of time.

For the observer on the ground compared with the observer on the train, both of their measurements will be different, individually, but they’ll be consistently different with one another. When you perform the calculations for how much time passes for one observer relative to the other, each observer will be able to correctly predict not only what their own watches and clocks say, but the other observer’s as well. All it takes is a knowledge of special relativity.

This photo shows Hafele, Keating, and their two atomic clocks on an around-the-world flight where they tested time dilation experimentally. An unidentified flight attendant looks on. This 1972 flight was the first experiment to directly measure directional time dilation, both due to special and general relativity combined.

The time that we perceive

When it comes to our perceptions, we know what it’s like to “experience” the passage of time. Even if time is relative to the observer, that would still imply its existence, it would just add a little bit of counterintuitiveness to a property that it possesses: its relativeness, which is a property that we’re largely unfamiliar with because of how slowly we typically move through space compared to the speed of light. However, it’s worth considering another idea: that our perception of time’s passage, or existence at all, is merely an illusion, driven by some other phenomenon besides a fundamental “ticking of a clock” that we use to measure the passage of time.

One particular perspective that’s interesting to consider is to look at the notions of symmetries in physics. One of the most profound theorems in all of physics is Noether’s theorem, which links symmetries in physics to conserved physical quantities. And one of the simplest physical systems to consider is that of a bouncing ball. If you watch a movie of a ball falling under the influence of gravity, you have no idea, all things being equal, of whether:

• time is running forward, and gravity is pulling the ball down from a dropped position,
• or time is running backward, and you’re viewing a ball that had previously been thrown upward while gravity resists its upward motion.

This is because the laws of motion obey what’s known as time-reversal symmetry: the laws are the same whether you run the clock forward or backward in time.

A ball in mid-bounce, as shown here, could be moving to the right and losing energy with each successive bounce, or could be moving to the left and gaining energy with each successive bounce. While Newton’s laws of motion are the same whether you run the clock forward or backward in time, not all of the rules of physics behave identically if you run the clock forward or backward.

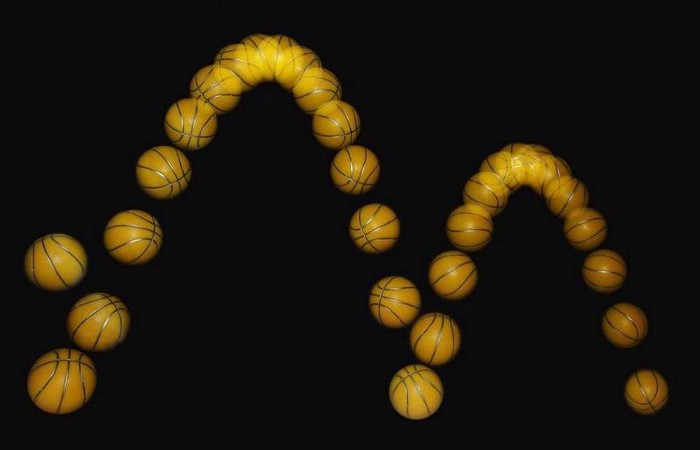
It isn’t just the laws of motion that obey time-reversal symmetries, but nearly all the laws of physics have that symmetry. Three of the four fundamental interactions in our Universe — gravitation, electromagnetism, and even the strong nuclear force — all obey this time-reversal symmetry. The laws that they obey are the same whether you run the clock forward or backward in time, and simply by watching the particles in your system evolve under these laws, you cannot discern which direction time is flowing in.

However, it turns out that there are two ways to identify a physical difference between systems that run either forward or backward in time. The first is by looking at reactions that proceed via the weak nuclear force, such as radioactive decays. Imagine that you have a heavy atomic nucleus, full of protons and neutrons. If there are a large number of neutrons in that nucleus compared to how many protons are present, there’s a chance that the nucleus will undergo a specific type of radioactive decay: beta decay.

Beta decay is what happens when one of the neutrons in the nucleus decays into a proton, an electron, and an antielectron neutrino, which happens for many elements and isotopes. Moreover, it even happens for free (unbound) neutrons that aren’t part of any larger atomic nucleus.

Schematic illustration of nuclear beta decay in a massive atomic nucleus. Only if the (missing) neutrino energy and momentum is included can these quantities be conserved. The transition from a neutron to a proton (and an electron and an antielectron neutrino) is energetically favorable, with the additional mass getting converted into the kinetic energy of the decay products. The inverse reaction, of a proton, electron, and an antineutrino all combining to create a neutron, never occurs in nature.

It will often happen that a neutron decays into a proton, an electron, and an antielectron neutrino. But it never happens that a proton, an electron, and an antielectron neutrino spontaneously react together to form a neutron. In fact, in a variety of ways, the weak interaction is the poster-child for time-asymmetric reactions in physics. It isn’t just beta decay in neutrons that violates a time-reversal symmetry, but all decays driven by the weak interaction.

The second way to identify whether a system is running forward or backward in time, however, is far more common and familiar. Each and every time we do something like:

• scramble and cook an egg,
• open the refrigerator door inside a heated house,
• or accidentally break a glass or porcelain vessel,

we create a situation where the entropy of our system has increased, or where the thermodynamic arrow of time has run forward.

You’ve likely heard of the concept of entropy as a “measure of disorder” of the physical system in question, but what’s happening internally is much more profound. Inside of any system, there’s some type of energy gradient. An unscrambled egg possesses an energy gradient between the albumen (the “white” of the egg) and the yolk, and the barrier around the yolk keeps them from mixing. An uncooked egg has potential energy stored in its molecules, and when you cook them, that (chemical) energy is released, forming new bonds and changing the structure of the egg. And there’s potential energy in the structure of a glass or porcelain vessel, and whenever it shatters, that potential energy gets released.

A wine glass, when vibrated at the right frequency, will shatter. This is a process that dramatically increases the entropy of the system, and is thermodynamically favorable. The reverse process, of shards of glass reassembling themselves into a whole, uncracked glass, is so unlikely that it never occurs spontaneously in practice. However, if the motion of the individual shards, as they fly apart, were exactly reversed, they would indeed fly back together and, at least for an instant, successfully reassemble the wine glass. Time reversal symmetry is exact in Newtonian physics, but is not obeyed in thermodynamics.

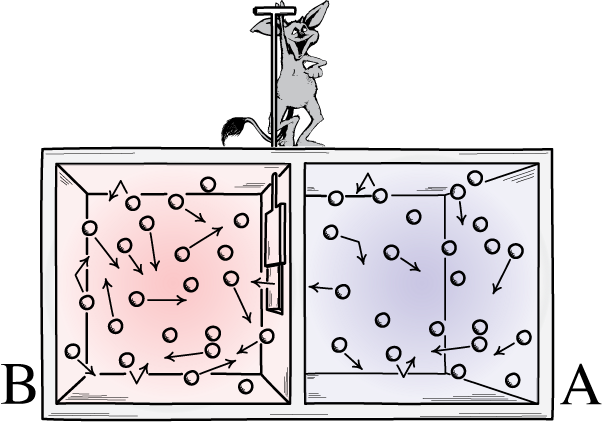
However, while it’s true that the thermodynamic arrow of time always points forward — the entropy of a closed, isolated system can never decrease, and only increases — it’s untrue that this either causes or is related to the perceived passage of time. We can test this by artificially decreasing the entropy within a system by having it not be closed and isolated, but rather by inputting energy into the system in such a way that the entropy within it decreases. For example, we can take a room filled with hot-and-cold particles, place a divider in the room, and allow a hole to open in the divider every time:

• a cold particle would move from the left side to the right,
• a hot particle would move from the right side to the left,

and to leave the divider closed in all other instances. Going from one large room of uniform temperature to a state where you have two separated rooms, one filled with hot particles on the left and one filled with cold particles on the right, represents a dramatic decrease in entropy. However, if you possessed any way of measuring the passage of time from anywhere within any of the rooms, you would find that your perceptions didn’t tell you that time was running backward at all, even though entropy was decreasing.

In other words, our perception of the flow of time — that it moves forward at the rate of one second per second for any observer — is unrelated to the thermodynamic arrow of time, and the increase (or not) of entropy.

This illustration shows two sides to a room: a hot one and a cold one, with a demon between them capable of opening and closing a divider between them. If the divider is opened, the gases will mix; if the gases were initially well-mixed, the demon opening-and-closing the divider could sort the room, even for a closed (but not isolated) system.

Is time an illusion?

So what about the old philosophical question, “If a tree falls in the woods and no one’s around, does it make a sound?” As Bart Simpson correctly noted, it absolutely does. Although the philosophical idea is that “sound” cannot exist without a “listener,” we now know that sound is simply a pressure wave made up of the collective motion of particles: either through the air, water, or solid Earth, and that it exists independent of whether there’s a listener (or observer) there to experience the “sound” effect for themselves. Macroscopic reality exists whether there’s an observer there to observe it or not.

However, this idea is not universally true down at the quantum level. There’s a famous experiment that has been performed — in many variations — since the 19th century: the double slit experiment. If you send a wave, like for example a water wave, through two slits, the part of the wave that propagates through will create an interference pattern on the other side. This works for not just classical waves, but for photons, electrons, and any other quantum particle that exhibits wave-like properties, even if you send them through the double slit one-at-a-time.

However, if you instead measure which slit each individual photon or electron passes through, you don’t get an interference pattern at all; just two “piles” of particles. It’s as though nature knows whether you’re observing it or not.

By setting up a movable mask, you can choose to either block one or both slits for the double slit experiment, seeing what the outcomes are and how they change with the motion of the mask. So long as both slits are unobscured and you don’t measure which “slit” particles go through, you’ll see the interference pattern.

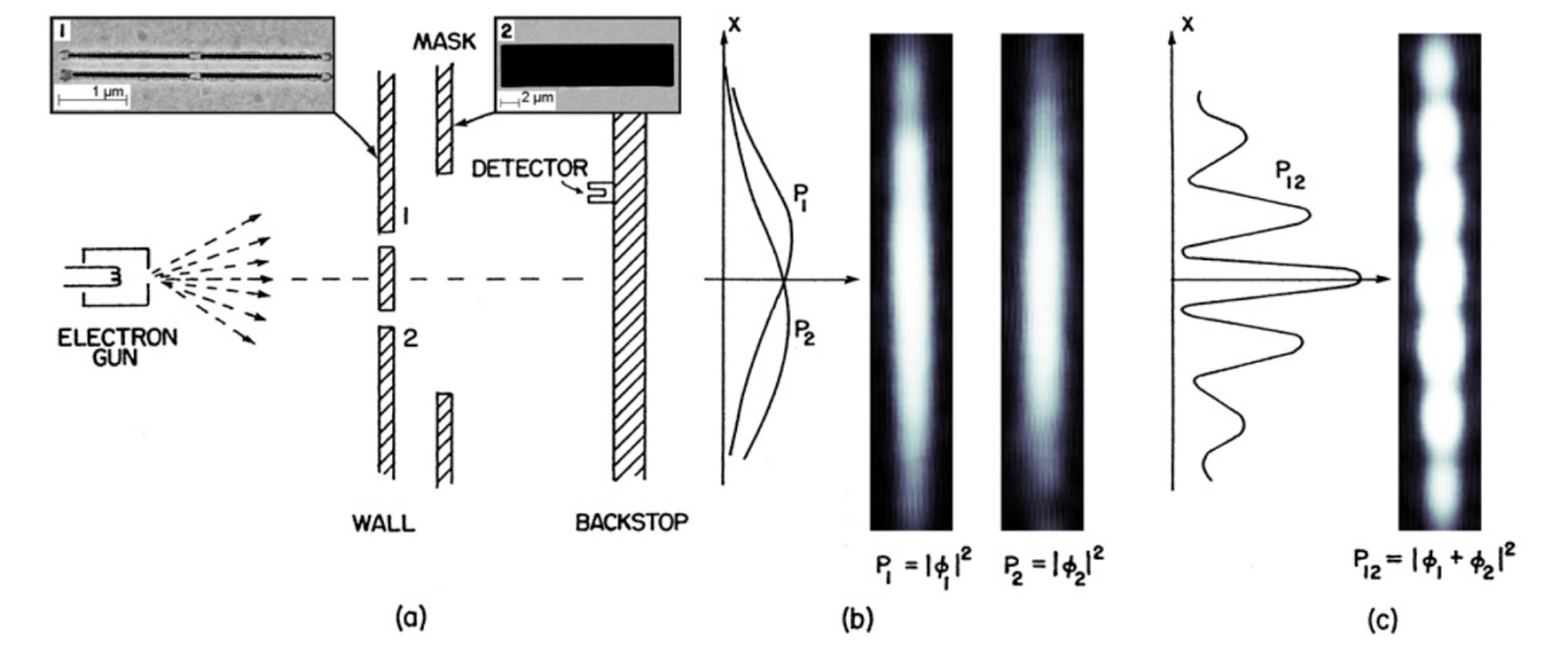
Could this be true for time as well? Could time itself not even exist unless — and until — there’s an observer there to measure it?

This seems wildly unlikely, and there’s a profound reason we can point to: direct observations of the early Universe. We know, from the laws of physics, that in the very early stages of the Universe, there were no observers at all. It took many events to unfold in order to bring anything capable of observing anything about, including:

• the creation of matter over antimatter,
• the formation of atomic nuclei,
• the formation of neutral atoms,
• the formation of many generations of stars in order to generate heavy elements,
• and for those heavy elements to undergo an extraordinary number of chemical reactions to create something capable of observing the Universe.

And all of those processes took at least a total of several hundred million years to complete, and probably billions of years given how slow life is to emerge and evolve. Yet, when we look out at the distant Universe, we see evidence that all of those things occurred very long ago: long before there were any observers around. This presents us with very strong evidence that time existed, in a real, physical sense, long before any observers arose. We have the luxury, with modern observatories, of going back and looking at that evidence — from the cosmic microwave background to the abundance of the light elements to the earliest stars and galaxies ever seen — any time we like.

JADES-GS-z14-0, in the top inset box, is found behind (and just to the right of) a closer, brighter, bluer galaxy. It was only through the power of spectroscopy with incredible resolution, capable of separating the two sources, that the nature of this record-breakingly distant object could be determined. Its light comes to us from when the Universe was only 290 million years old: just 2.1% of its current age. JADES-GS-z14-1, just below it, comes from when the Universe was ~300 million years old. Compared to large, modern-day galaxies, all early galaxies contain a paucity of stars.

The one way time may be illusory is this: it is still possible that it’s what we call an emergent property of the Universe, rather than a fundamental one. We think of space, time, and particles (quanta) as fundamental entities within the Universe, while quantities that can be further derived from them — such as entropy — are emergent properties. However, there are alternative formulations that are mathematically feasible, where you can do things like treat entropy as fundamental, and then other properties, including time, can be derived as emergent ones. Although time and entropy both clearly exist from a physical point of view, it is not necessarily clear which one is fundamental and which one is emergent; that’s not something we know how to test at present.

However, we can be pretty confident that time does indeed exist, at least at some level. When physics asks about whether or not something exists, the questions we usually ask include:

• Can you measure it?
• Can you quantify it?
• Can you define it in a mathematically self-consistent way?
• Is it, itself, an observable quantity?
• And do other observable quantities depend on this one in an inextricable way?

From the quantum to the macroscopic to the cosmic, the answer to all of these questions is “yes” when it comes to time. Although there are many oddities to its behavior, and many insufficiencies in any definition we attempt to assign to it (similarly to energy), everything we can observe, measure, and test about it points to its reality. If it truly is an illusion, it’s an illusion that’s fooled even our best methods of understanding our physical existence so far.

Send in your Ask Ethan questions to startswithabang at gmail dot com!