The most basic unknowable property of matter
The quantum nature of the Universe ruins everything.
“What we observe is not nature itself, but nature exposed to our method of questioning.” –Werner Heisenberg
When you think about the Universe on a global scale, you might think of the very large (like stars, galaxies, or clusters of galaxies), the very small (like cells, molecules, or individual atoms), or anywhere in between. The Universe, as you well know, encompasses it all.

Acknowledgements: Ming Sun (UAH), and Serge Meunier, via http://www.spacetelescope.org/news/heic1404/.
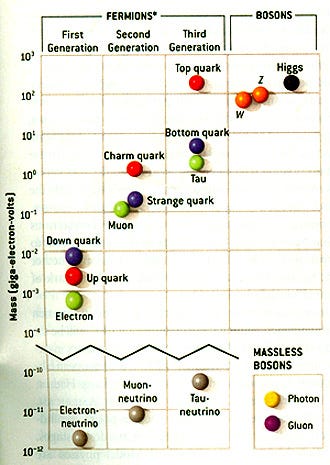
But at a fundamental level, one of the greatest things about it is it’s all made up of the same stuff, in the sense that the building blocks of all forms of matter are the same few fundamental particles. If we’re willing to ignore whatever it is that dark matter happens to be, we’re talking about only a small table of fundamental particles: the ones in the Standard Model of elementary particles.
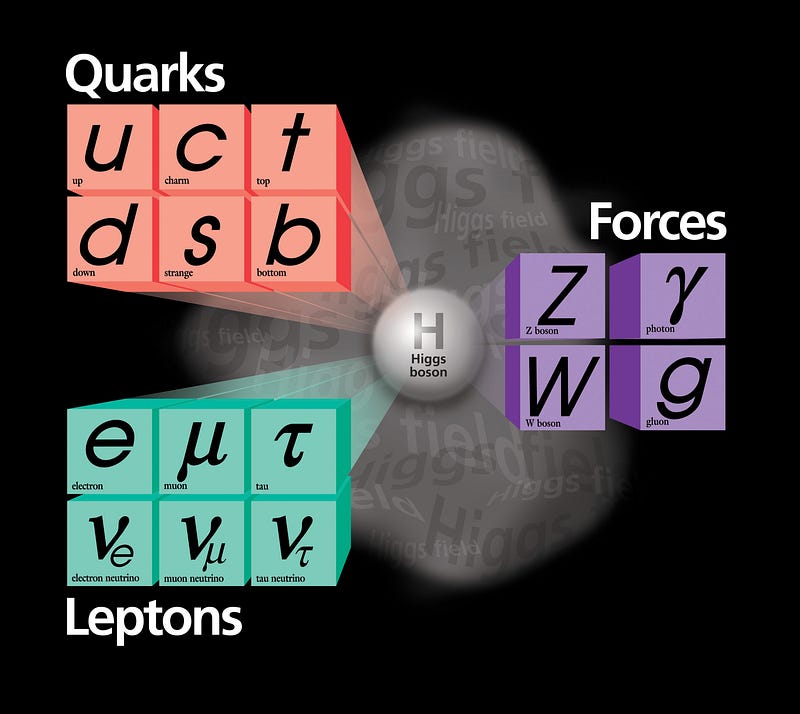
Most of these particles, however, aren’t easily or freely found in nature. Sure, there are neutrinos, electrons, and the photon that we can observe in isolation, and up and down quarks (along with the gluons) are what make up protons, neutrons and atomic nuclei; those are common enough. But the vast majority of Standard Model particles — including all the heavier quarks, the muon and the tau, and the W and Z bosons — are fundamentally unstable. As it turns out, their lifetimes are not only finite, but tiny compared to our macroscopic world. Let me explain, and let’s do it by starting with a phenomenon that you’ve heard of before: radioactivity.

You might be familiar with radioactive decay, and the fact that heavy, unstable elements can decay into lighter ones. Some of these decays are fast, taking less than a second, while others can take billions of years. (With some ultra-rare decays taking billions of times the present age of the Universe.) But these are composite configurations of a mix of up-and-down quarks along with gluons — manifested in terms of protons and neutrons — that are at most turning one or two down quarks into (slightly lighter) up quarks. This takes a long time because the particle exchange that allows this to happen is a weak force decay, mediated by a very heavy particle (the W-boson).
How does this work?
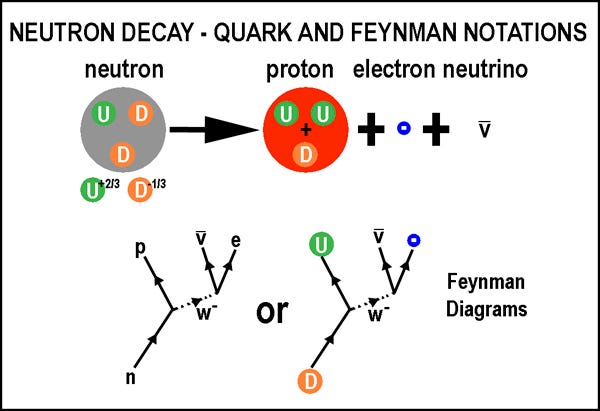
Let’s say you have a neutron, a collection of two down quarks and one up quark. With a mean lifetime of about 15 minutes, neutrons decay into protons, which are two up quarks and one down quark. We tend to measure nuclear energies in terms of units of MeV (Mega electron-Volts, or one million electron-Volts), and the mass difference between a neutron and a proton is just a little bit over 1 MeV. [All masses are given in natural units, without the factors of the speed of light (c) thrown in there.]
On the other hand, the interaction that causes a decay is a down quark transforming into an up quark plus an electron/antineutrino pair, something that requires a W-boson. But these particles don’t have sufficient energy to make a W-boson; the mass of a W-boson is somewhere around 80 GeV, or 80,000 MeV! In order for this radioactive decay to proceed, it’s dependent on there being a quantum fluctuation that allows this to happen, something that only occurs very rarely because of that huge mass ratio of the proton/neutron difference to the mass of the W-boson.
But none of the unstable fundamental particles have such a small mass difference. A muon is the next longest lived particle (after the neutron), but the mass difference between it and the electron is a little over 100 MeV, and its lifetime is just 2.2 microseconds. When I say, “a relatively short amount of time,” fundamental particles live anywhere from 10^(-6) seconds to timescales as short as an appalling 10^(-25) seconds!
As it turns out, these short lifetimes are of huge importance for a very specific fundamental property of these particles: their mass.
You may have heard of Heisenberg’s uncertainty principle, and it has nothing to do with the chemistry teacher from Breaking Bad. Most commonly, it’s known in the form of a joke:
Heisenberg is driving in his car, when he sees the flashing lights of a cop car behind him. He pulls over, and the officer comes up to him.
Officer: “Do you know how fast you were going?”
Heisenberg: “No, but I know exactly where I am!”
This is because there’s an inherent tension — an uncertainty — between knowing (or measuring) the position and the momentum of any system in the Universe simultaneously. The better you know (or measure) the position of a particle, the greater an uncertainty it induces in that particle’s momentum!
Lesser known, but just as important, is a joke that’s a little bluer:
Heisenberg finds himself at couples therapy with his wife. The therapist asks him what the problem is, but he’s too embarrassed to answer. So…
Therapist: “Mrs. Heisenberg, what’s going on at home.”
Mrs. Heisenberg (sighing): “Whenever he has the time, he doesn’t have the energy. And whenever he has the energy, he doesn’t have the time!”
This is because there’s that same inherent tension-and-uncertainty between energy and time as there is between position and momentum! So if you have a very small uncertainty in the timescale of a particular system, there must inherently be a very large energy uncertainty.
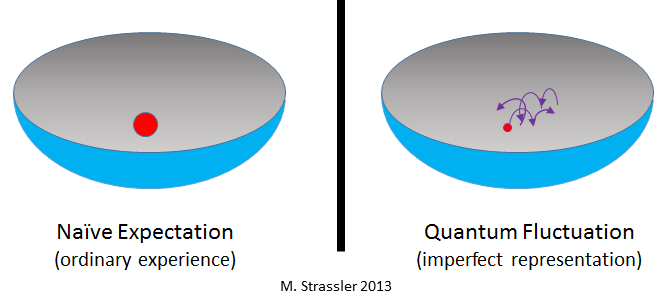
Think about this in terms of a particle’s lifetime, now. If a particle stably (or quasi-stably) exists for a very long period of time, its energy uncertainty can be very small. But what of an inherently short-lived, very unstable particle? Its energy uncertainty must be huge to compensate; Heisenberg demands it.
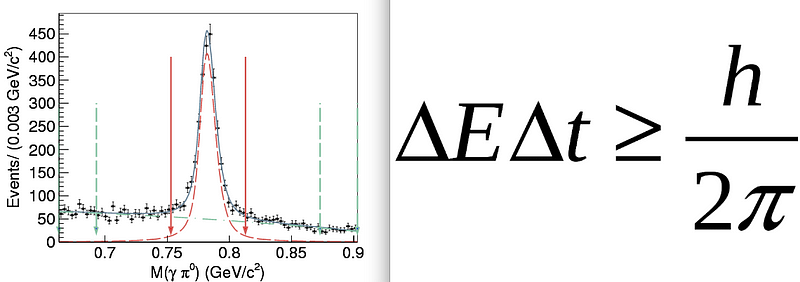
And now for the kicker: if there’s a large uncertainty in a particle’s inherent energy, and we know that there’s an energy-mass equivalence via E = mc^2, then the shorter a particle’s lifetime is, the less well-known its mass can be, even in principle!
When we create a very short-lived particle like a W-or-Z-boson, a top quark or a Higgs boson, we can know what its mass will be on average, but any individual particle created will have a range of masses it can take on. In other words, when we say “this particle’s mass is 91.187 GeV” (for the Z-boson, for instance), we’re saying that this is the average mass value that all Z-bosons have, but any one individual particle will vary considerably!
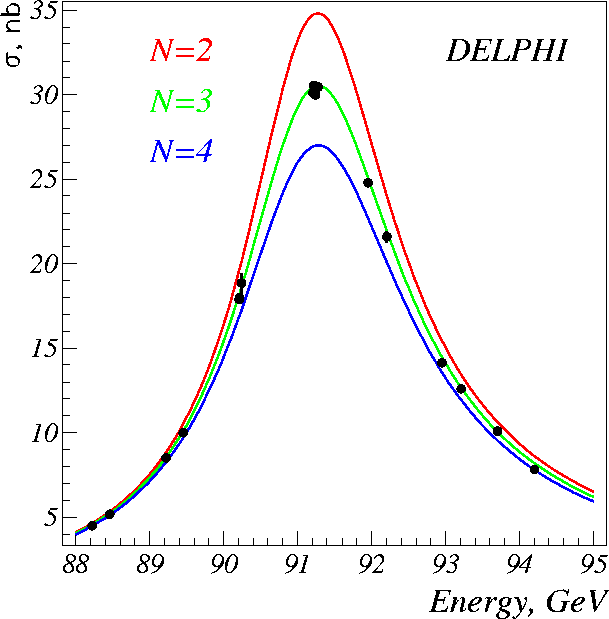
This is why, even today, it’s very hard to know the average mass of the Higgs boson, the top quark or the W-boson to three or four significant figures; even a few good, clean events won’t tell us anything more than a range. This is also why unstable particles not only have a mass as a fundamental property, but a width, which represents the inherent quantum uncertainty in their mass. Believe it or not, this was first worked out all the way back in 1936!
This may not explain the mystery of why the scale says I’m five pounds heavier today than I was yesterday, but it does tell us something amazing about the Universe: that for unstable particles, even a property as fundamental as a particle’s mass in unavoidably, significantly and inherently variable. And we owe it all to the inescapable quantum nature of the Universe!
Leave your comments at the Starts With A Bang forum on Scienceblogs.