The surprising origins of wave-particle duality

One of the most powerful, yet counterintuitive, ideas in all of physics is wave-particle duality. It states that whenever a quantum propagates through space freely, without being observed-and-measured, it exhibits wave-like behavior, doing things like diffracting and interfering not only with other quanta, but with itself. However, whenever that very same quantum is observed-and-measured, or compelled to interact with another quantum in a fashion that reveals its quantum state, it loses its wave-like characteristics and instead behaves like a particle. First discovered in the early 20th century in experiments involving light, it’s now known to apply to all quanta, including electrons and even composite particles such as atomic nuclei.

But the story of how we discovered wave-particle duality doesn’t begin and end in the early 20th century, but rather goes back hundreds of years: to the time of Isaac Newton. It all began with an argument over the nature of light, one that went unresolved (despite both sides declaring “victory” at various times) until we came to understand the bizarre quantum nature of reality. While wave-particle duality owes its origin to the quantum nature of the Universe, the human story of how we revealed it was full of important steps and missteps, driven at all times by the only source of information that matters: experiments and direct observations. Here’s how we finally arrived at our modern picture of reality.

What appears to be a simple plane wave, such as light or water passing through a partly obscured barrier, was conceived of (brilliantly) by Christiaan Huygens as a series of waves that propagate spherically outward, all superimposed atop one another. This idea of wave mechanics would apply not only to scalar waves such as water waves, but to light and particles as well.

Huygens: light is a wave

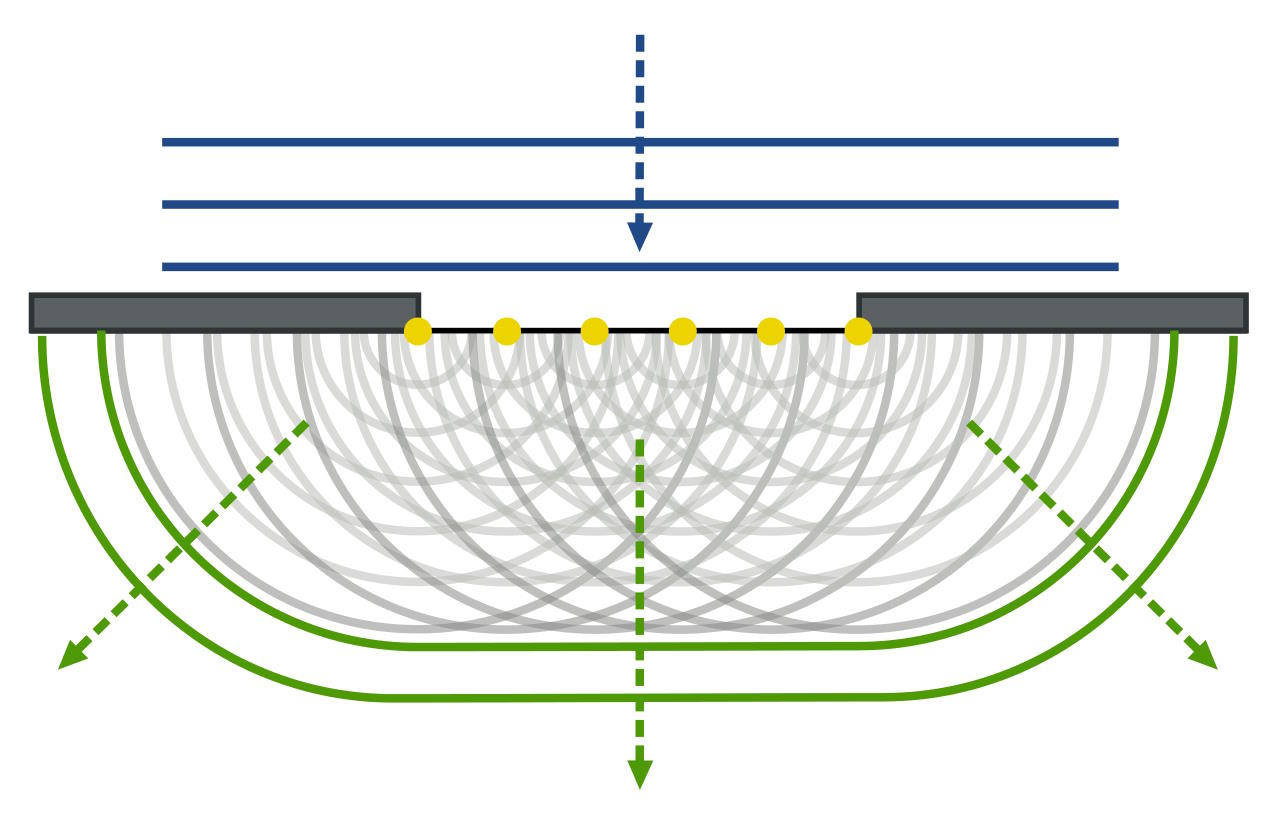
Picture a wave propagating through water, such as in the ocean: it appears to move linearly, at a particular speed and with a particular height, only to change and crash against the shore as the water’s depth lessens. Back in 1678, Dutch scientist Christiaan Huygens recognized that these waves could be treated — rather than as linear, coherent entities — as a sum of an infinite number of spherical waves, where each spherical wave became superimposed atop one another along the propagating wavefront. (Illustrated above.)

Huygens noted the existence of phenomena like interference, refraction, and reflection, and saw that they applied equally well to water waves as they did to light, and so he theorized that light is a wave as well. This provided the first successful explanation of both linear and spherical wave propagation, both for water waves as well as for light waves. However, Huygens’ work had limitations to it, including:

• it could not explain why the waves only propagated forward, not backward as well,
• he could not explain “edge effects,” or why and how diffraction occurred,
• and his idea of light could not explain the existence of polarization, which is easily observed as sunlight reflects off of bodies of water.

The idea that “light is a wave” was born with Huygens and became quite popular across the European continent upon his treatise’s publication in 1690, but didn’t catch on elsewhere due to the presence of a much more famous competitor.

Light passing from a negligible medium through a dense medium, exhibiting refraction. Light comes in from the left, strikes the prism and partially reflects (top), while the remainder is transmitted through the prism and exits at right. The light that passes through the prism appears to bend, as it travels at a slower speed than the light traveling through air did earlier. When it re-emerges from the prism, it refracts once again, returning to its original speed. Note that different wavelengths correspond to different colors, and that they are separated by their passage through the prism, not before nor after.

Newton: light is a corpuscle

In 1704, Newton published his treatise on Opticks, based on experiments that he first presented in 1672. Instead of a wave, Newton was able to describe light as a series of rays, or corpuscles, that behaved in a particle-like fashion. The deductions made in Newton’s Opticks arise as direct inferences from the experiments performed, and focused on the phenomena of refraction and diffraction. By passing light through a prism, Newton was the first to show that light was not “inherently white” and altered to have color by its interactions with matter, but rather that white light itself was composed of all of the different colors of the spectrum, which he did by passing white light through a prism.

He performed experiments on refraction with prisms and lenses, on diffraction with closely-spaced sheets of glass, and on color mixtures with both lights of individual colors that were brought together and with pigment powders. Newton was the first to coin the “ROY G. BIV” palette of colors, noting that white light could be broken up into red, orange, yellow, green, blue, indigo, and violet. Newton was the first to understand that what appears to us as color arises from the selective absorption, reflection, and transmission of the various components of light: what we now know as wavelength, an idea antithetical to Newton’s conception.

This diagram, dating back to Thomas Young’s work in the early 1800s, is one of the oldest pictures that demonstrate both constructive and destructive interference as arising from wave sources originating at two points: A and B. This is a physically identical setup to a double slit experiment, even though it applies just as well to water waves propagated through a tank.

Young’s double slit experiment

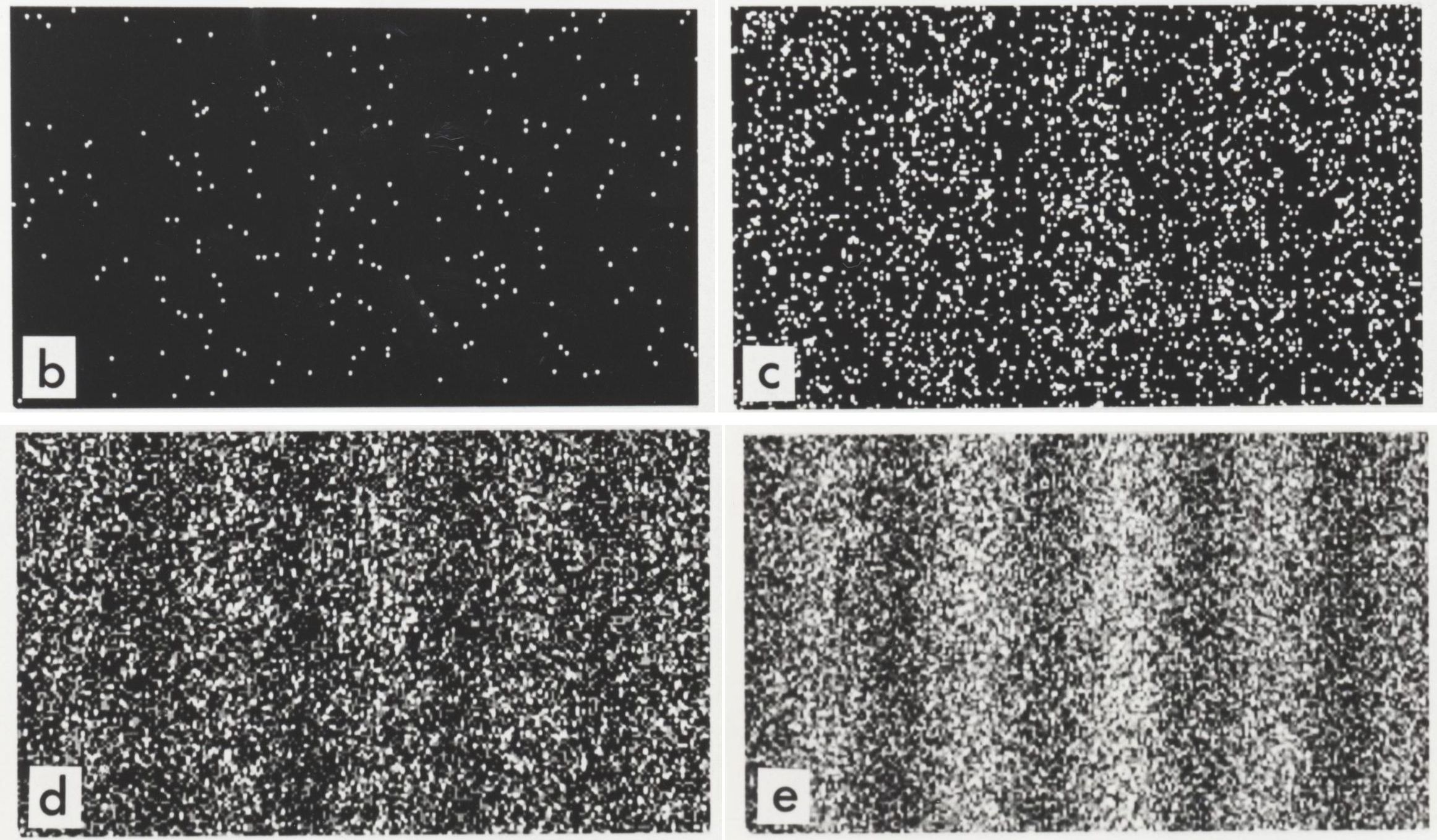
Throughout the 1700s, Newton’s ideas became popular worldwide, heavily influencing Voltaire, Benjamin Franklin, and Lavoisier, among others. But at the end of the century, from 1799 to 1801, scientist Thomas Young began experimenting with light, making two enormous advances in our understanding of light in the process.

The first, arguably most famous advance, is illustrated above: Young performed what’s known as the double slit experiment with light for the first time. By passing light of a monochrome color through two closely spaced slits, Young was able to observe a phenomenon that’s only explicable through wave behavior: the constructive and destructive interference of that light in the pattern it produces, in a fashion that depends on the color of the light being used. Young was further able to prove, through quantitative investigation, that what we perceive as the color of light is, in fact, determined by the wavelength of that light: that wavelength and color, barring the mixture of different colors, were directly related to one another.

While Newton’s conception of light still had its advantages, it was clear that the wave theory of light had its advantages too, and succeeded where Newton’s corpuscular theory did not. The mystery would only deepen as the 19th century unfolded.

Light of different wavelengths, when passed through a double slit, exhibit the same wave-like properties that other waves do. Changing the wavelength of light, as well as changing the spacing between the slits, will change the specifics of the pattern that emerges.

Simeon Poisson and the world’s most absurd calculation

In 1818, the French Academy of Sciences held an essay competition on uncovering the nature of light, and physicist Augustin-Jean Fresnel decided to enter. In that competition, he wrote an essay detailing the wave theory of light, quantitatively, accounting for Huygens’ wave principle and Young’s principle of interference in the process. He was able to account for the effects of diffraction within this framework as well, adding in the principle of superposition to his essay, explaining the scintillating colors of stars as well.

Initially, however, one of the adherents to Newton’s corpuscular idea who was serving as a judge on the committee, Simeon Poisson, attempted to have Fresnel laughed out of the competition. (Despite the fact that the only other entrant, who remains anonymous more than 200 years later, was ignorant of Young’s work.) Poisson was able to show that, according to Fresnel’s theory, if you took:

• monochromatic light,
• passed it through a diverging lens to widen the beam,
• and passed that beam around a spherical obstacle,

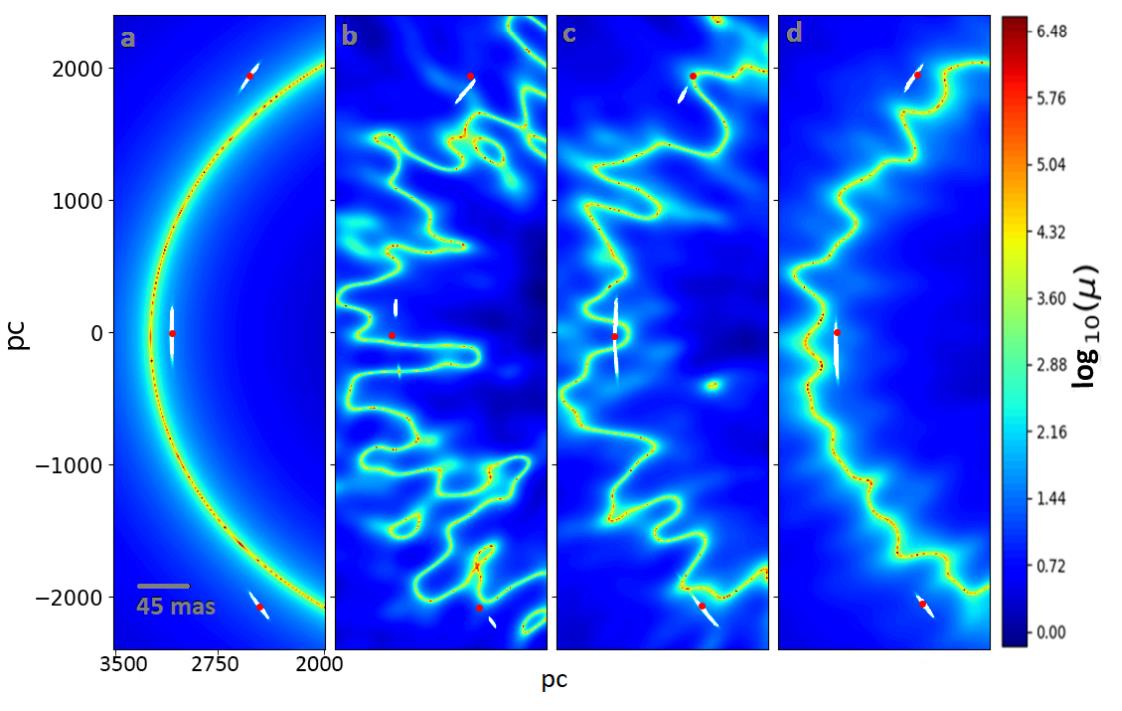
then Fresnel’s theory would predict that rather than a solid shadow, there would be a bright, luminous point in the shadow’s center. Even worse, that point would be just as bright as the part of the beam lying outside of the sphere’s shadow. Clearly, Poisson reasoned, this idea is absurd, and therefore light simply cannot have a wave nature to it.

The results of an experiment, showcased using laser light around a spherical object, with the actual optical data. Note the extraordinary validation of Fresnel’s theory’s prediction: that a bright, central spot would appear in the shadow cast by the sphere, verifying the absurd prediction of the wave theory of light. Logic, alone, would not have gotten us here.

François Arago shows the absurdity of experiment

However, there were five men on the committee, and one of them was François Arago: abolitionist, politician, and a man who would, in 1848, become President of France. Arago was moved by Poisson’s argument against Fresnel’s idea, but not in the reductio ad absurdum sense that Poisson intended. Instead, Arago became motivated to actually perform the experiment himself: to create a monochromatic light source, widen it in a spherical fashion, and pass it around a smooth, small sphere, to see what the results of the experiment were.

To the great surprise of perhaps all, Arago’s experiment revealed that the spot does in fact exist! Moreover, it:

• appears of identical brightness to the unobstructed light,
• varies in size only as a function of the light’s wavelength, distance to the screen, and size of the sphere,
• and additionally contains concentric, faint rings that result from further interference arising from the various wavefronts.

Huygens’ ideas had finally been placed on a solid theoretical footing, and had been developed into a full-fledged theory that could now account for phenomena such as polarization. Over the course of the 1800s, the wave nature of light became widely accepted in scientific circles.

Light is nothing more than an electromagnetic wave, with in-phase oscillating electric and magnetic fields perpendicular to the direction of light’s propagation. The shorter the wavelength, the more energetic the photon, but the more susceptible it is to changes in the speed of light through a medium.

Maxwell demonstrates how light is a wave

The 1800s were also a spectacular time for advances and discoveries in the fields of electricity and magnetism. The work of Ampere, Faraday, Gauss, Coulomb, Franklin, and many others laid the groundwork for what would arguably be the 19th century’s greatest scientific achievement: the development of Maxwell’s equations and the science of electromagnetism. Revelations included:

• charged particles create electric fields,
• charged particles in motion create electric currents,
• electric currents create magnetic fields,
• changing magnetic fields induce electric currents,
• and changing electric fields induce what Maxwell called a displacement current, or a magnetic field that responds in a particular fashion.

One of the consequences of Maxwell’s equations, as was shown in the 1870s, is that there would be some sort of electromagnetic radiation that arose under the right conditions: radiation that was made of oscillating, in-phase electric and magnetic fields that propagated at one universal speed, which happens to be the speed of light in a vacuum. At last, we had what appeared to be a full explanation: light wasn’t just a wave, but an electromagnetic wave, that always traveled at one universal speed, the speed of light.

The photoelectric effect details how electrons can be ionized by photons based on the wavelength of individual photons, not on light intensity or any other property. Above a certain wavelength threshold for the incoming photons, regardless of intensity, electrons will be kicked off. Below that threshold, no electrons will be kicked off, even if you turn the intensity of the light way up. Both electrons and the energy in each photon are discrete.

Einstein demonstrates that light’s energy is quantized

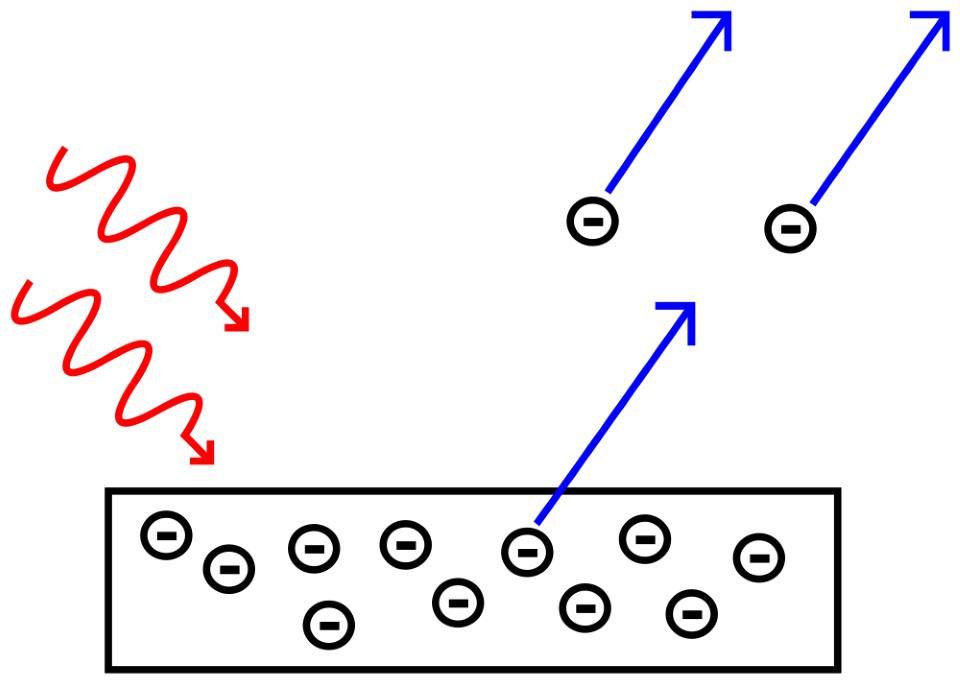
Of course, physics didn’t end with the discovery of classical electromagnetism, and the dawn of the 1900s would bring with it the earliest stages of the quantum revolution. One of the key aspects of this new conception of our reality came from none other than Albert Einstein himself, whose 1905 treatise on the photoelectric effect would forever change our understanding of light. Taking a conducting metal plate, Einstein was able to show that shining light on it caused electrons to spontaneously be emitted from the metal, as though these electrons were being “kicked off” by the light that struck them. Clearly, with enough energy, the electrons were becoming unbound from the metal they were a part of

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

What Einstein did next was nothing short of brilliant.

• When he varied the intensity of the light, he noted that this changed the number of electrons kicked off, but not whether they were kicked off.
• When he varied the wavelength of the light, he noted that beyond a certain wavelength, no electrons would get kicked off, irrespective of how high the intensity got.
• And when he varied the wavelength of light in the opposite direction, to short wavelengths, he noted that electrons were always kicked off, irrespective of how faint and dim the intensity got.

It was as though light was made up of individual energy “packets,” known today as photons, which carry energy in proportion to their frequency. (Or, inversely proportional to their wavelength.) Even though light propagated as a wave, it interacted with matter like a corpuscle (or particle), bringing about the beginnings of the modern idea of wave-particle duality.

The wave pattern for electrons passing through a double slit, one-at-a-time. If you measure “which slit” the electron goes through, you destroy the quantum interference pattern shown here. However, the wave-like behavior remains so long as the electrons have a de Broglie wavelength that’s smaller than the size of the slit they’re passing through. This wave-like and particle-like behavior has been demonstrated for electrons, photons, and even larger, composite entities.

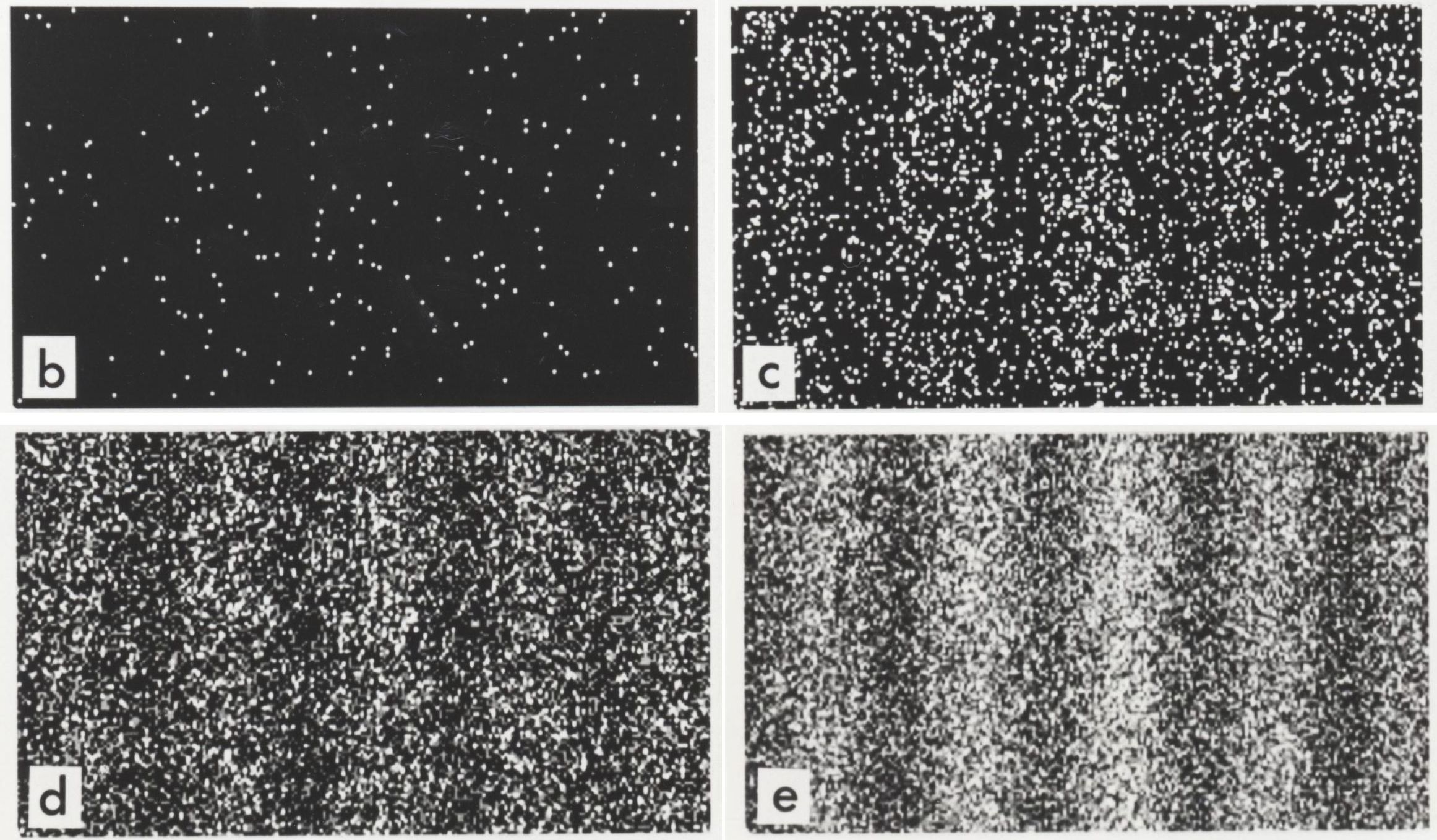
The modern double-slit and the dual nature of reality

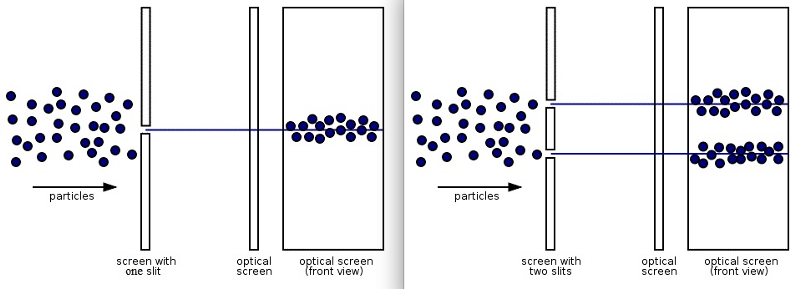
It turns out that photons, electrons, and all other particles exhibit this odd quantum behavior of wave-particle duality, where if you observe-and-measure them during their journey, or otherwise force them to interact and exchange energy-and-momentum with other quanta, they behave as particles, but if you don’t, they behave as waves. This is perhaps exemplified by the modern version of Young’s double-slit experiment, where it doesn’t rely on monochromatic light, but can even be performed with single particles, like photons or electrons, passed through a double slit one-at-a-time.

If you perform this experiment without measuring your particles until they reach the screen, you’ll find that they do, in fact, reproduce the classic interference pattern once you’ve accumulated enough individual quanta. Bright spots, which correspond to the locations where large numbers of particles land, are spaced apart by dark bands, where few-to-no particles land, consistent with the notion of an interference pattern.

However, if you measure whether the quantum passes through “slit #1” or “slit #2” during its journey, you no longer get an interference pattern on the screen, but simply two lumps: one lump corresponding to particles that passed through the first slit and the other corresponding to particles that passed through the other.

If you measure which slit an electron (or a photon) goes through when performing a one-at-a-time double slit experiment, you don’t get an interference pattern on the screen behind it. Instead, the electrons behave not as waves, but as classical particles. A similar effect can be seen for single-slit (left) experiments as well.

Many have commented that “It’s like nature knows whether you’re watching it or not!” And in some sense, this counterintuitive statement is actually true. When you don’t measure a quantum, but rather simply allow it to propagate, it behaves like a wave: a classical wave that interferes with not just other waves but also itself, exhibiting wave-like behavior such as diffraction and superposition. However, when you do measure a quantum, or otherwise compel it to interact with another quantum of high-enough energy, your original quantum behaves like a particle, with a deterministic, particle-like trajectory that it follows, just as tracks in particle physics detectors reveal.

So, is light a wave or a particle?

The answer is yes: it’s both. It’s wave-like when it’s freely propagating, and it’s particle-like when it’s interacting, a set of phenomena that’s been probed in an enormous variety of ways over the past ~100 years or so. Despite the proposal of hidden variables to attempt to reconcile wave-particle duality into a single deterministic framework, all experiments point to nature still being non-deterministic, as you cannot predict the outcome of an unmeasured, wave-like trial with any more accuracy than the Schrödinger’s equation’s probabilistic approach. Wave-particle duality began in the 1600s, and despite our attempts to pin down the true nature of reality, the answer that the Universe itself reveals is that our quantum reality is both, simultaneously, and really does depend on whether or not we measure or interact with it.