Scientists Admit, Embarrassingly, We Don’t Know How Strong The Force Of Gravity Is

Every physical theory has constants in it. The gravitational constant is remarkably uncertain.
When we first began formulating physical laws, we did so empirically: through experiments. Drop a ball off a tower, like Galileo may have done, and you can measure both how far it falls and how long it takes to hit the ground. Release a pendulum, and you can find a relationship between the pendulum’s length and the amount of time it takes to oscillate. If you do this for a number of distances, lengths, and times, you’ll see a relationship emerge: the distance of a falling object is proportional to the time squared; the period of a pendulum is proportional to the square root of the pendulum’s length.
But to turn those proportionalities into an equal sign, you need to get that constant right.
In these examples, as well as many others, that constant-of-proportionality is related to G, the gravitational constant. The Moon orbits the Earth, the planets orbit the Sun, light bends due to gravitational lensing, and comets lose energy as they escape from the Solar System all in proportion to G. Even before Newton came along, in the 1640s and 1650s, Italian scientists Francesco Grimaldi and Giovanni Riccioli made the first calculations of the gravitational constant, meaning it was the first fundamental constant ever determined: even prior to Ole Rømer’s determination of the speed of light in 1676.
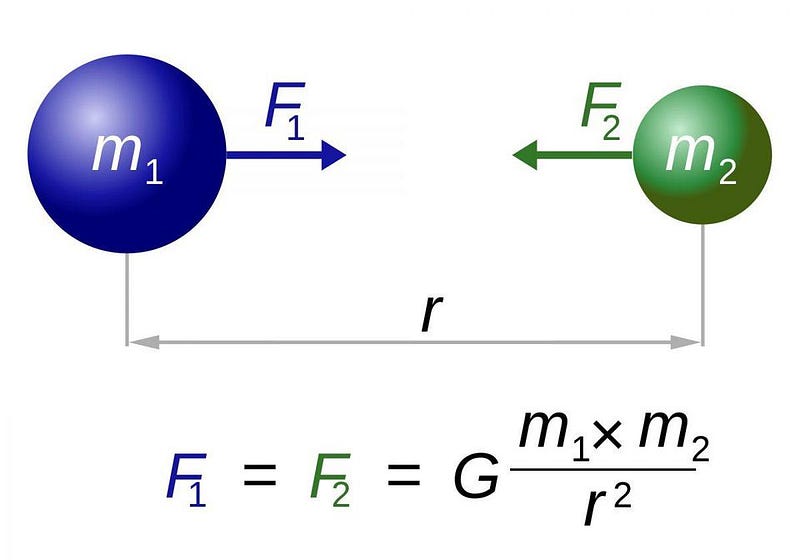
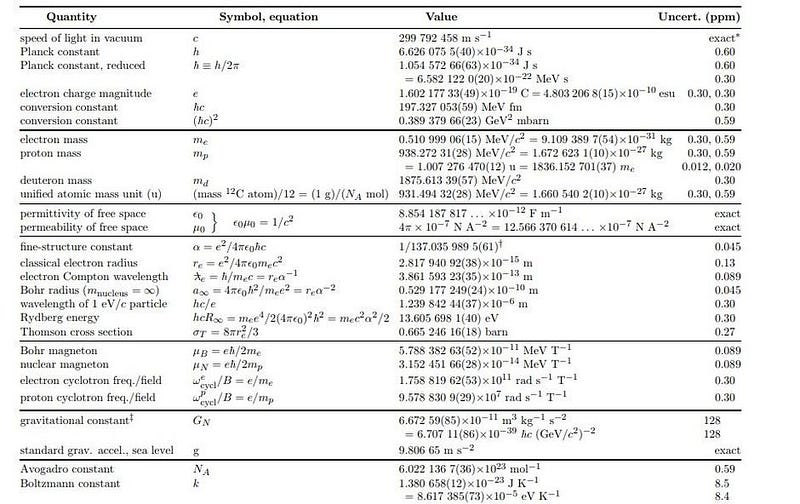
When you take any two masses in the Universe and place them in proximity to one another, they attract. According to Newton’s laws, valid under all but the most extreme mass (for large masses) and distance (for small distances) conditions in all of nature, the force of attraction is related to the two masses, the separation between them, and G, the gravitational constant. Over the centuries, we’ve refined our measurements of a great many fundamental constants to tremendous precision. The speed of light, c, is known exactly: 299,792,458 m/s. Planck’s constant, ħ, which governs quantum interactions, has a value of 1.05457180 × 10^-34 J⋅s, with an uncertainty of ±0.000000013 × 10^-34 J⋅s.
But G? That’s a different story entirely.

In the 1930s, G was measured to be 6.67 × 10^-11 N/kg²⋅m², later refined in the 1940s to 6.673 × 10^-11 N/kg²⋅m², both by the scientist Paul Heyl. As you might expect, the values got better and better through time, with the uncertainties dropping from 0.1% to 0.04% all the way down to just 0.012% in the late 1990s, owing mostly to the work of Barry Taylor at NIST.
In fact, if you pull out an old copy of the Particle Data Group booklet, where they give the fundamental constants, you can find a value for G in there that looks good: 6.67259 × 10^-11 N/kg²⋅m², with an uncertainty of just 0.00085 × 10^-11 N/kg²⋅m².
But then something funny happened.
Later that year, experiments that were performed indicated a value that was inconsistently high with those values: 6.674 × 10^-11 N/kg²⋅m². Multiple teams, using different methods, were getting values for G that conflicted with each other at the 0.15% level, more than ten times the previously reported uncertainties.
How did this happen?
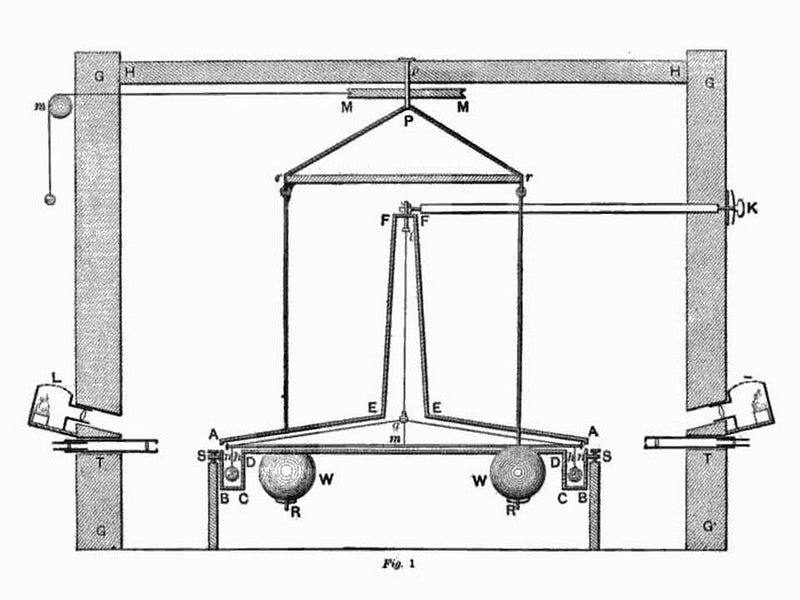
The first accurate measurement of the gravitational constant, independent of other unknowns (like the mass of the Sun or the mass of the Earth), only came about with Henry Cavendish’s experiments in the late 18th century. Cavendish developed an experiment known as a torsion balance, where a miniature barbell was suspended by a wire, perfectly balanced. Near each of the masses on either end were two larger masses, which would gravitationally attract the small masses. The amount of torsion that the miniature barbell experienced, so long as the masses and distances were known, would allow us to measure G, the gravitational constant, experimentally.
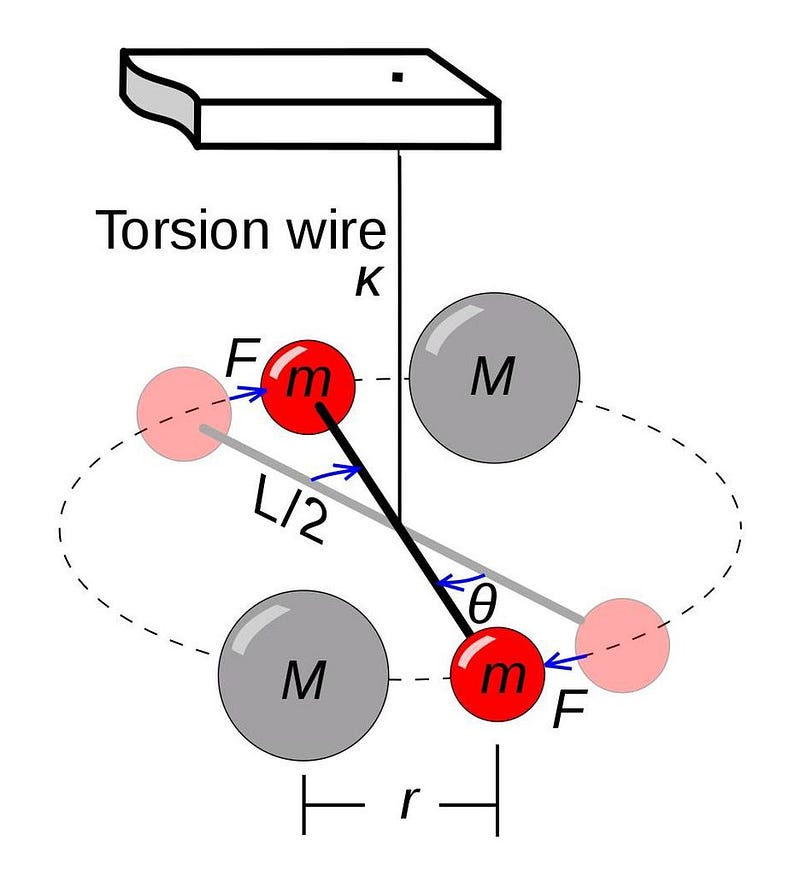
It is strongly suspected that one of the major factors at play was the well-known psychological factor of confirmation bias. If all of your colleagues are getting measurements like 6.67259 × 10^-11 N/kg²⋅m², you might reasonably expect to get something like 6.67224 × 10^-11 N/kg²⋅m², or 6.67293 × 10^-11 N/kg²⋅m², but if you got something like 6.67532 × 10^-11 N/kg²⋅m², you’d probably assume you did something wrong.
You’d look for possible sources of error, until you found one. And you’d perform the experiment again and again, until you got something reasonable: something that was at least consistent with 6.67259 × 10^-11 N/kg²⋅m².
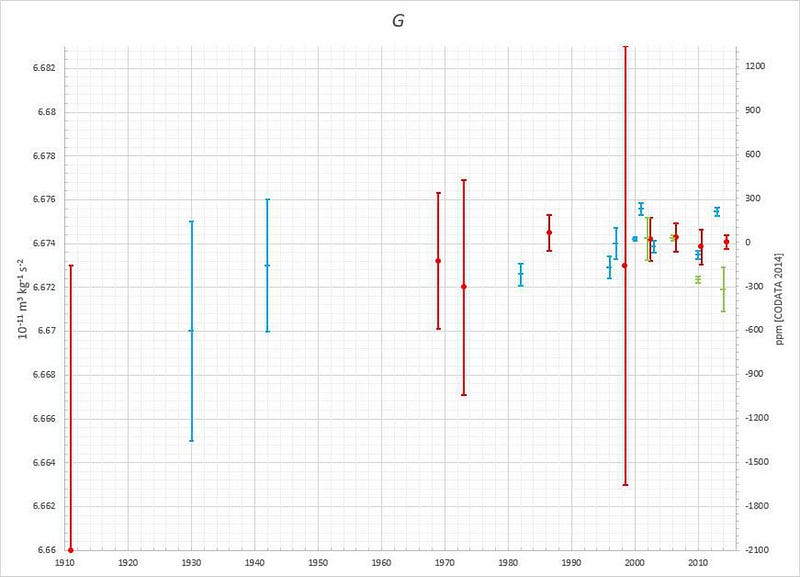
This is why it was such a shock, in 1998, when a very careful team got a result that differed by a spectacular 0.15% from the previous results, when the errors on those earlier results were claimed to be more than a factor of ten below that difference. NIST responded by throwing out the previously stated uncertainties, and values were suddenly truncated to give at most four significant figures, with much larger uncertainties attached.
Torsion balances and torsion pendulums, both inspired by the original Cavendish experiment, continue to lead the way in measurements of G, outpacing the more recent technique of atom interferometry experiments. In fact, just last week, a team from China claimed to get the most precise measurement of G yet from two independent measurements: 6.674184 × 10^-11 N/kg²⋅m² and 6.674484 × 10^-11 N/kg²⋅m², with uncertainties of just 11 parts-per-million on each.
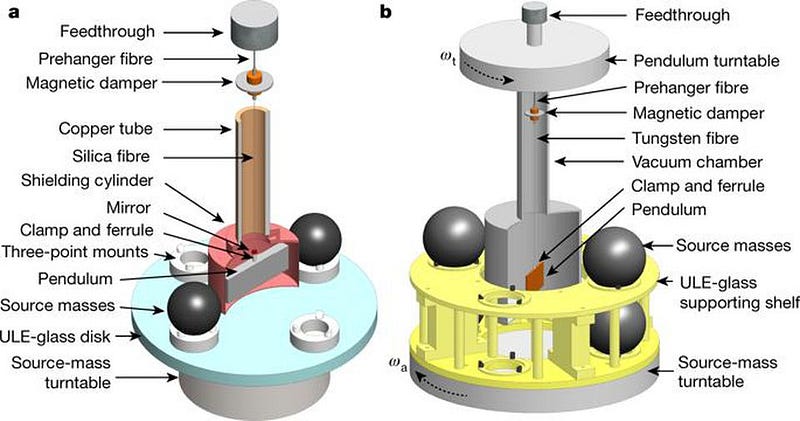
These values may agree with one another to within two standard deviations, but they don’t agree with other measurements performed by other teams over the past 15 years, which range from as high as 6.6757 × 10^-11 N/kg²⋅m² and as low as 6.6719 × 10^-11 N/kg²⋅m². While the other fundamental constants are known to precisions of anywhere between 8 and 14 significant digits, uncertainties are anywhere from thousands to billions of times greater when it comes to G.
The gravitational constant of the Universe, G, was the first constant to ever be measured. Yet more than 350 years after we first determined its value, it is truly embarrassing how poorly known, compared to all the other constants, our knowledge of this one is. We use this constant in a whole slew of measurements and calculations, from gravitational waves to pulsar timing to the expansion of the Universe. Yet our ability to determine it is rooted in small-scale measurements made right here on Earth. The tiniest sources of uncertainty, from the density of materials to seismic vibrations across the globe, can weave their way into our attempts to determine it. Until we can do better, there will be an inherent, uncomfortably large uncertainty anywhere the gravitational phenomenon is important. It’s 2018, and we still don’t know how strong gravity actually is.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.