Ask Ethan: Is it possible that gravity isn’t quantum?

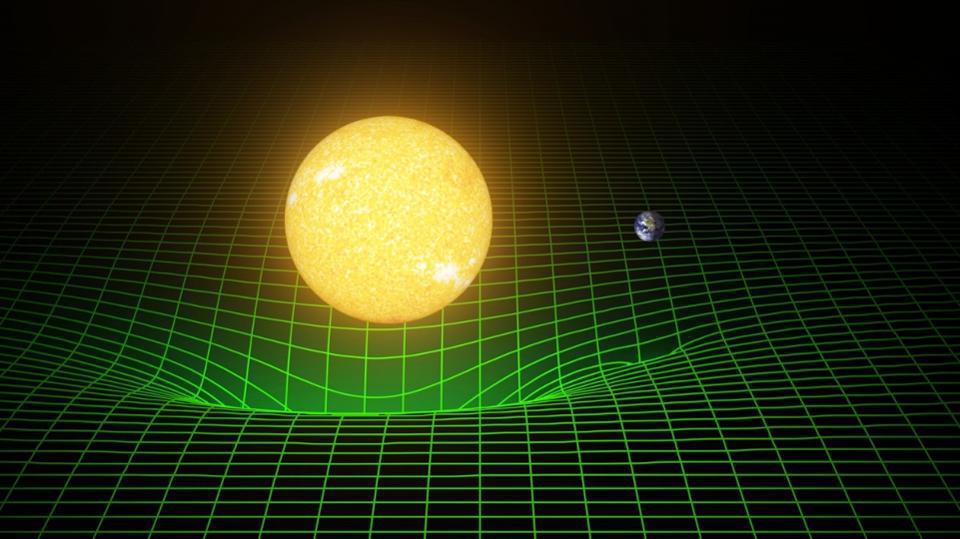
The two greatest leaps of 20th century physics still leave physicists grappling to understand how it’s possible, at a fundamental level, that they can coexist. On the one hand, we have Einstein’s general theory of relativity (GR), which treats space as a continuous, smooth background that’s deformed, distorted, and compelled to flow and evolve by the presence of all the matter and energy within it, while simultaneously determining the motion of all matter and energy within it via the curvature of that background. On the other hand, there’s quantum physics, governed at a fundamental level by quantum field theory (QFT). All the quantum “weirdness” is encoded in that description, including ideas like quantum uncertainty, the superposition of states, and quantum indeterminism: fundamentally anti-classical notions.

Traditionally, approaches to unify the two have focused on quantizing gravity, attempting to place it on the same footing as the other quantum forces. But a series of new papers, led by Jonathan Oppenheim, takes a very different approach: creating a “postquantum” theory of classical gravity. It’s led to questions by many, including Patreon supporters Cameron Sowards and Ken Lapre:

“I’d love to see your thoughts about the just published postquantum theory of classical gravity.”

“[A]ny chance you have the time and inclination to explain this paper in English so non-physicists could take a stab at understanding it?”

It’s a big idea that, importantly, is still in its infancy, but that doesn’t mean it doesn’t deserve consideration. Let’s first look at the problem, and then, the proposed solution inherent to this big idea.

A mural of the Einstein field equations, with an illustration of light bending around the eclipsed sun, the observations that first validated general relativity four years after it was first theoretically put forth: back in 1919. The Einstein tensor is shown decomposed, at left, into the Ricci tensor and Ricci scalar, with the cosmological constant term added in after that. Novel tests of new theories, particularly against the differing predictions of the previously prevailing theory, are essential tools in scientifically testing an idea.

It’s often said that general relativity (GR) and quantum field theory (QFT) are incompatible, but it’s difficult for many to understand why. After all, for problems that are only concerned with gravity, using GR alone is perfectly sufficient. And for problems that are only concerned with quantum behaviors, using QFT alone (which normally assumes a flat background for spacetime) is perfectly sufficient. You might worry that the only problems would occur when you were considering quantum behaviors in regions of space where spacetime was more severely curved, and even when you encountered those regimes, you could intuit a way out.

Why, for example, couldn’t you have space (or spacetime) always obey the laws of GR, and then have all your quantum particles-and-fields exist within that spacetime, where they obey the quantum laws (given by QFT) of the Universe? That’s the approach that many have taken, including Stephen Hawking, which is how he derived the infamous effect of Hawking radiation: by calculating how quantum fields behaved in the severely curved (classical) spacetime outside of a black hole’s event horizon. Known as semiclassical gravity, this approach is valid in many regimes, but it still doesn’t take you everywhere.

For the real black holes that exist or get created in our Universe, we can observe the radiation emitted by their surrounding matter, and the gravitational waves produced by the inspiral, merger, and ringdown. The electromagnetic radiation that we see solely originates from outside the event horizon itself; the Hawking radiation that black holes are predicted to emit is thus far unobservable in practice.

It doesn’t tell you what happens at or very close to singularities: where general relativity breaks down and gives answers that make no sense. It doesn’t tell you what happens when you have quantum fluctuations on the smallest of scales — below the Planck scale, for example — where every fluctuation should be so energetic on such tiny scales that a black hole should eventually form. And it doesn’t tell you how gravity behaves for systems that are inherently quantum in nature. That last one is extremely important, because while we lack technology to get very close to singularities or probe sub-Planckian scales, we deal with inherently quantum systems, including ones made out of massive (gravitating) particles, all the time.

Consider, for example, a double slit experiment: where individual particles, even one-at-a-time, are fired at two very narrow, closely-spaced, slits.

• If you measure which slit each particle goes through, it will wind up in one of two locations: one corresponding to a path where it goes through slit #1 and another corresponding to a path where it goes through slit #2.
• If you don’t measure which slit each particle goes through, it behaves as though it passes through both slits simultaneously, interfering with itself in the process, and landing in a location described, probabilistically, by a wavefunction on the other side.

This works for photons, electrons, or heavier, composite particles, too. This behavior, within the double slit experiment, is right at the heart of quantum mechanics.

Inherently quantum systems, such as an individual electron passing through a double slit, are generally very computationally expensive to simulate on a classical computer. It’s these types of systems that hold the most potential for Quantum Advantage to give real, important speed-ups as far as simulations and computations go.

But now let’s ask a slightly deeper question: what about gravity? What happens to the gravitational field of a massive particle as it travels through a double slit?

If you measure which slit the particle travels through, the answer is easy to intuit: the particle’s gravitational field just corresponds to wherever it was at any point along its trajectory, as it passed through the slit and onto the screen behind it.

But what if you don’t measure which slit the particle goes through?

This is a big challenge, because with plain old GR and QFT alone, we don’t get an answer. Does the gravitational field split, interfere with itself, and curve space the way you’d expect a quantum mechanical entity to: as though it were distributed in a probabilistic, wave-like distribution across a wide range of spatial locations? That would be an indication that gravity is inherently quantum in nature. On the other hand, if it simply followed a well-defined classical trajectory, that would be an indication that not only isn’t gravity inherently quantum, but it would have tremendous implications for how we conceive of the behavior of particles, as it might provide evidence for some sort of hidden determinism buried deep within quantum physics.

If you have a quantum state of a massive particle that’s in one of two positions, but has not had the entanglement/superposition of states broken yet, there are two possibilities for how a gravitational “test particle” will attract: either toward one state or the other, at left, or toward the average value, at right. This experiment has not been performed.

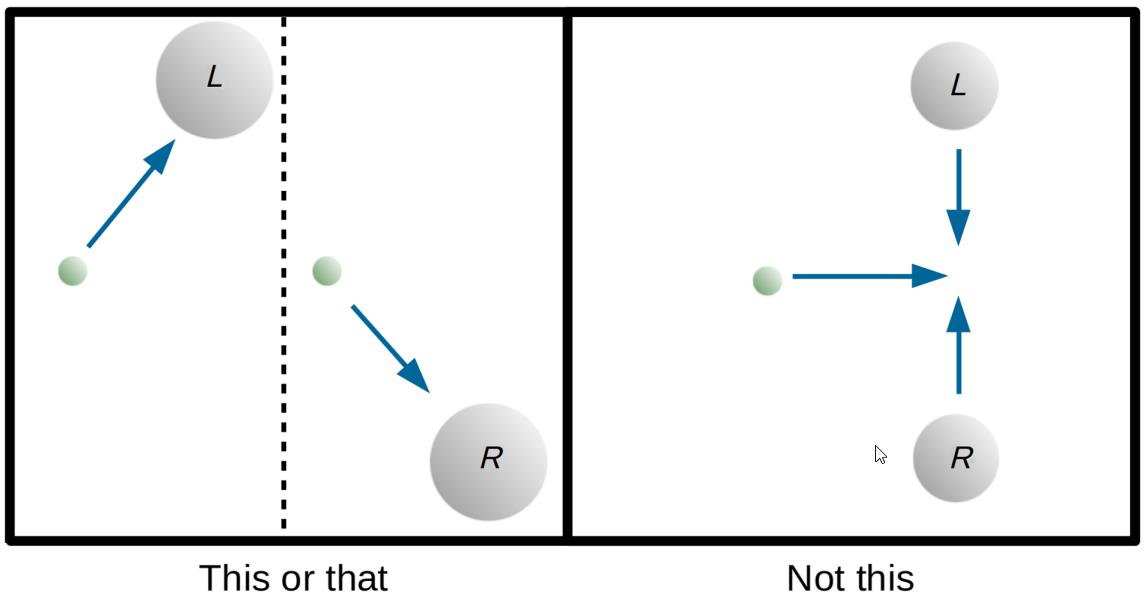
Which one is it that will occur, then, when it comes to gravity? This idea was first explored in a paper by Don Page and C.D. Geilker all the way back in 1981, who cooked up a thought experiment involving a radioactive lead mass in a superposition of states, a Geiger counter that would cause the quantum system to decohere (or collapse the wavefunction, if you prefer), and a test mass that would gravitate. The possible outcomes are shown above.

• If the test mass gravitates toward either of the two possible final-state locations that it’s in a superposition of, as shown at left, that would indicate that quantum mechanics is purely a statistical effect, and that massive-enough particles have determinate positions, and gravitate accordingly.
• If the test particle instead falls down the middle, as shown at right, that indicates that the semiclassical prediction is what occurs: the “average” trajectory taken by the test mass is what determines the gravitational effects of the particle.

If enough time is allowed to pass before the entanglement is broken (or the superposition of states decoheres), a high-quality experiment should be able to tell the left-hand case from the right-hand case, and should teach us whether gravity is at least partly quantum (for the case at right) or whether gravity is deterministic all the way through (corresponding to the case at left). Unfortunately, this is not an experiment that we know how to perform just yet; it’s a thought experiment only.

If you fire a quantum particle through a double slit and don’t measure which one it goes through, it will behave in a quantum fashion all the way until it hits the screen at the back, producing a probability distribution that shows an interference pattern. If you make measurements along the way, gravitationally, what will happen is not yet known.

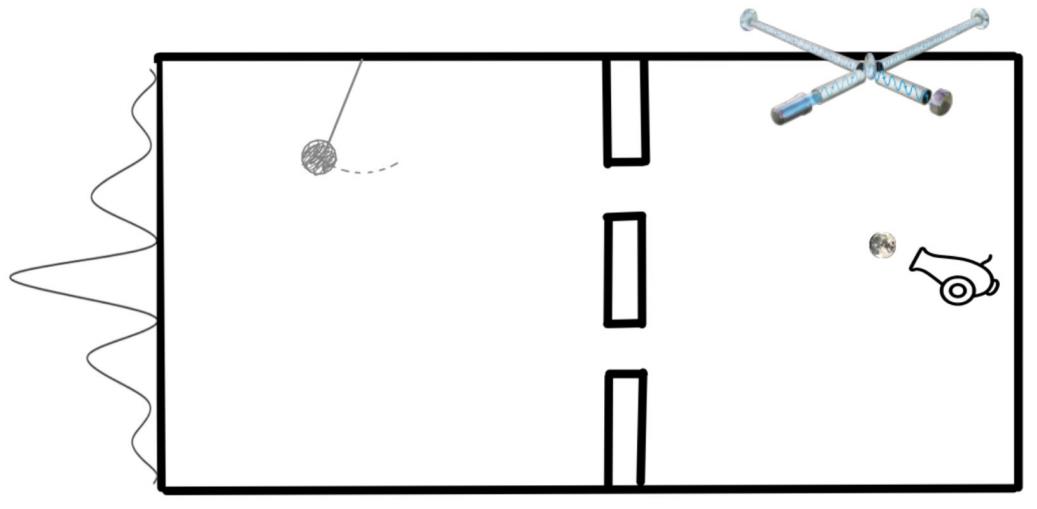
You can perform a similar thought experiment with a different setup: this time, imagine that you have a particle passing through a double slit, interfering with itself, and arriving on the screen. Even with such an uncertain position, there can be a well-defined (and knowable, to high-precision) momentum associated with the particle. If the gravitational field produced by this particle is classical, you can measure the gravitational field to sufficiently high-precision, determining the particle’s position without disturbing it. If you can make that measurement, it should be sufficient to reveal which slit the particle went through.

Either particles would be prevented from being in a superposition, or you would violate the uncertainty principle by knowing two complementary qualities (like position and momentum) to too great a precision.

But what if the classical field doesn’t respond to the quantum system in a deterministic way? What if the gravitational field reacts in an indeterministic way to the presence of matter? We have assumed, perhaps without saying so explicitly, that the gravitational degrees of freedom contain complete information about the location of the relevant particles.

But that may not be absolutely true. It’s possible that they contain only partial information, and that’s what makes the new idea of Oppenheim and his current-and-former students worth exploring.

The event horizon of a black hole is a spherical or spheroidal region from which nothing, not even light, can escape. But outside the event horizon, the black hole is predicted to emit radiation. Hawking’s 1974 work was the first to demonstrate this, and it was arguably his greatest scientific achievement. Although this treatment isn’t dependent on whether spacetime and gravity are quantum or not, treating gravity semiclassically has pathological consequences under a variety of circumstances.

Oppenheim himself states as much, noting in his new paper that:

“…previous arguments for requiring the quantization of the space-time metric implicitly assume that theory is deterministic, and are not a barrier to the theory considered here.”

The alternative, as he puts forth, is known as stochasticity. In fact, the related paper to his main paper proves this rigorously: that classical-quantum dynamics requires stochasticity, or to involve random processes (that we normally attribute solely to quantum systems) as an inherent part of how they interact.

Consider what this might mean for a longstanding paradox: the black hole information paradox. In short, this paradox is about the fact that the particles that fall into and give rise to a black hole contain particle properties: which is a form of information. Over time, black holes decay, and decay by the emission of blackbody radiation: Hawking radiation. Either:

• information is not destroyed, and is somehow encoded into the outgoing radiation,
• or information is destroyed (and not conserved),

and in either case, the big question we’re all looking to answer is “how.” What is it that occurs, and how does it occur?

Encoded on the surface of the black hole can be bits of information, proportional to the event horizon’s surface area. When the black hole decays, it decays to a state of thermal radiation. As matter and radiation fall into the black hole, the surface area grows, enabling that information to be successfully encoded. When the black hole decays, entropy will not decrease, but rather will remain constant, as Hawking radiation is an entropy-conserving (adiabatic) process.

If the Universe is fully deterministic, then gravity will break down at low energies.

If gravity is semiclassical, then a pure quantum state (where information is preserved) will evolve to become a mixed state (where information is lost), and therefore information loss occurs.

But none of the attempts to resolve the information-loss paradox have been theories of gravity, and one issue that always comes up whenever you include gravity is that of backreaction: when what occurs on quantum scales influences spacetime, how do those spacetime changes then back-react onto influencing those very same quantum scales?

That’s what the new set of papers is all about. I don’t want to go through the gory details of evaluating the new ideas on their specific merits, because that’s not really the core issue. Whenever you propose a radically new idea, there are going to be a large number of:

• pathologies, where you can point to specific examples/aspects of known physics that aren’t properly described by your idea at first,
• incompletenesses, where your theory has nothing valuable to say about a number of important issues,
• and outright failures, where you can point to apparent contradictions within the initial framework.

That’s okay; that’s what you get every time you present a new idea, as a fully-formed, complete theory is far beyond the scope of any sort of initial work.

The quantum fluctuations that occur during inflation get stretched across the Universe, and when inflation ends, they become density fluctuations. This leads, over time, to the large-scale structure in the Universe today, as well as the fluctuations in temperature observed in the CMB. It took years of theory development from when the idea was first put forth before all of these predictions could be teased out, as well as until certain pathologies with inflation’s original formulation could be resolved.

Alan Guth’s initial paper on inflation was fraught with problems, but it was an idea that led to a revolution because of the power it had to resolve issues that were unresolvable up to that point.

Many of the early attempts to formulate quantum theories were faced with pathologies, including attempts made by luminaries like Bohr and Schrodinger.

The first attempts at quantum electrodynamics were riddled with mathematical inconsistencies.

But these are not dealbreakers; this is what you get pretty much every time you “play in the sandbox” of theory with new ideas. It’s something that comes with the territory, and we shouldn’t demand that someone get everything right, and iron out all the supporting details, before an idea sees the light of day. Yes, it’s true that for a new theory to supplant and overthrow the previous prevailing model of reality, there are three hurdles it must clear:

1. It must reproduce all of the successes of the old model.
2. It must explain problems or puzzles that the old model cannot successfully explain.
3. And it must make new predictions, that can then be observed and/or tested, that differ from those of the old model.

But that’s what the development of a new idea looks like at the end of the story: once the matter is settled. We are in a very different stage here when it comes to postquantum gravity: the stage where the theory is still being developed. This is a new idea that has some compelling reasons to look deeper into it, and it’s important not to stomp it out of existence before we’ve even decided whether it’s fertile ground or not.

It’s generally assumed that at some level, gravity will be quantum, just like the other forces. But it’s possible that gravity is inherently classical, and that there are important ways that quantum processes, even involving the other forces, feed back (or backreact) onto spacetime, affecting gravity itself.

Although there has been a violent knee-jerk reaction from many against this idea, it’s often worth considering what happens if we throw out certain assumptions, and ask whether this truly leaves us with something pathological, or whether it might be salvageable after all. While semiclassical gravity does have those pathologies, this postquantum approach — of classical gravity coupled to QFTs, but where the dynamical laws of quantum mechanics are modified in ways that may still fit within experimental and observational constraints — should be further explored.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

One of the reasons it’s promising is because what’s traditionally been called “the measurement problem” in quantum physics, where reality isn’t determined until a measurement takes place, is replaced by the interaction of classical spacetime with quantum degrees of freedom, which is sufficient to cause decoherence in quantum systems. It also eliminates a host of “quantum gravity” problems by hypothesizing that gravity is not quantum at all.

Will it be possible to test/constrain the idea, as the authors of the second paper assert, via interferometry experiments and/or precision measurements of supposedly-static masses over time? That remains to be seen, but it isn’t crazy to pursue this idea. Remember: most ideas in theoretical physics are not new, and most new ideas are not good, and it’s not like the ideas we’ve had about how to reconcile GR with QFT have borne fruit up until this point. This one, regardless of how it shakes out, actually is a new idea, and it’s worth diving into the details to determine whether it’s a good one or not before simply dismissing it.

Send in your Ask Ethan questions to startswithabang at gmail dot com!