The grand paradox at the heart of every black hole

When something falls into a black hole, where does it go, and will it ever come back out again? According to Einstein’s General Relativity, those answers are simple: as soon as anything physical — matter, antimatter, radiation, etc. — crosses over the event horizon, it’s gone. It can add things like mass, electric charge, and angular momentum to the black hole, but little else. It goes swiftly toward and eventually into the central singularity, and will never escape again.

But our Universe isn’t governed by General Relativity alone, but also by quantum physics. According to our best understanding of quantum reality, there’s much more that needs to be considered. Not only are there other quantum properties inherent to the raw ingredients that go into making a black hole — baryon number, lepton number, color charge, spin, lepton family number, weak isospin and hypercharge, etc. — but the fabric of spacetime itself, which contains the black hole, is quantum in nature. Because of those quantum properties, black holes do not remain static, but rather evaporate over time: emitting Hawking radiation (and perhaps even more) in the process.

When black holes do evaporate, then, what happens to the information that went into creating them? Is it conserved? Is it destroyed? Is it encoded in the outgoing radiation? And if so, how? These questions are at the heart of perhaps the greatest paradox of all: the black hole information paradox. Here’s both what we know and what we still need to find out.

When two particles are entangled in the quantum mechanical sense, it’s as though some sort of hidden, invisible connection exists between them, and that a seemingly “random” property of one member of the pair can be known to better than “random guessing” simply by measuring the properties of the other member. Entanglement, as far as we can tell, is instantaneous, although no actual information appears to ever be transmitted from one member of the pair to the other.

Information

When a physicist talks about information, they don’t necessarily mean what we conventionally think of as information: a string of letters, numbers, symbols, or anything else that can be encoded with bits like 0s or 1s. Conventionally, this is often described as “the number of yes/no questions that must be answered to fully specify the properties of your physical system,” although even that description has limitations. These are all certainly examples of information, but those examples don’t encompass all the various types of information that exist. Information can also include:

• signals that enforce causality,
• quantum states (like qubits instead of bits) for individual entities,
• entangled quantum states between multiple entities,
• or any measure of the physical quantity known as entropy.

That last one is tricky, because entropy — an inherently thermodynamical quantity — is very often misunderstood. You’ll often hear statements like “entropy is a measure of disorder” or “entropy always increases for any system” and while those things are kind of true, it’s possible to make very ordered high-entropy systems and to decrease a system’s entropy through the input of an external energy source.

As an alternative, consider this: what entropy actually measures is the number of possible arrangements of the (fully quantum) state of your system.

A system set up in the initial conditions on the left and allowed to evolve will have less entropy if the door remains closed (left) than if the door is opened (right). If the particles are allowed to mix, there are more ways to arrange twice as many particles at the same equilibrium temperature than there are to arrange half of those particles, each, at two different temperatures, resulting in a much greater entropy for the system at right than the one at left.

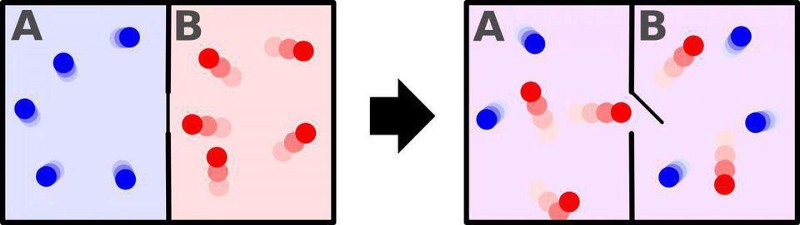
A classic example is to consider two systems:

1. A room with a divider in it, where one side of the room is filled with hot gas and the other side is filled with cold gas.
2. And that same room, with the same gases, except the divider is open and both sides of the room have reached the same temperature.

Both systems have the same number of particles, the same total energy in them, but wildly different entropies from one another. The second system has a much greater amount of entropy, as there are many different ways to distribute energy among all of the particles in your system to achieve the desired configuration than there are for the first system; the number of possible arrangements of the fully quantum state of your full system is much greater for the second system than the first.

Because there is a greater number of possible arrangements, you have to provide a greater amount of information — and, therefore, answer a greater number of “yes/no” questions — to fully describe the system with a greater amount of entropy. Information and entropy aren’t identical, but they are proportional: a greater entropy to your system means it requires more information to fully describe it.

A wine glass, when vibrated at the right frequency, will shatter. This is a process that dramatically increases the entropy of the system, and is thermodynamically favorable. The reverse process, of shards of glass reassembling themselves into a whole, uncracked glass, is so unlikely that it never occurs spontaneously in practice. However, if the motion of the individual shards, as they fly apart, were exactly reversed, they would indeed fly back together and, at least for an instant, successfully reassemble the wine glass. Time reversal symmetry is exact in Newtonian physics, but is not obeyed in thermodynamics.

Information and black holes

If you take a book and burn it, the book’s information doesn’t get lost or destroyed, but merely scrambled. In principle — although, maybe not in practice just yet — you could trace each and every particle of paper-and-ink that went into the fire, determine where they went, and from the ash, soot, chemicals, and invisible gases they produced, keep track of every character on every page in that book. In principle, you could look at that final system of the completely burned book and reconstruct the complete information that was in the book before you burned it.

You can do this with the remnants of a shattered glass, reconstructing what the original, unbroken structure looked like. You can do this with a scrambled-and-cooked egg, reconstructing what the uncooked, unscrambled egg was like. As long as the fundamental particles that the original system was made out of were preserved, no matter what interactions they underwent in the meanwhile, that original information about the initial state of the system would be preserved as well.

But with black holes, that absolutely isn’t the case any longer. In General Relativity, black holes don’t have any memory about the types of particles (or the properties of those particles) that went into creating or growing the black hole. The only measurable properties a black hole can possess are mass, electric charge, and angular momentum.

One of the most important contributions of Roger Penrose to black hole physics is the demonstration of how a realistic object in our Universe, such as a star (or any collection of matter), can form an event horizon and how all the matter bound to it will inevitably encounter the central singularity. Once an event horizon forms, the development of a central singularity is not only inevitable, it’s extremely rapid.

In the early 1970s, this puzzle was considered by physicist Jacob Bekenstein, who recognized why this was such a problem. Whatever particles go into forming a black hole have their own properties, configuration, and amount of entropy (and information) encoded within them. According to the second law of thermodynamics, entropy can never decrease for a closed system; it can only increase or remain the same, unless some external source of energy is inputted to decrease that entropy. (And even then, the total entropy of “the original system plus the external source,” where the external source is where that inputted energy comes from, will continue to increase.)

But in pure General Relativity, black holes have zero entropy, and that definition simply won’t work. From the perspective of an external observer, it’s quantum particles that go into the creation of a black hole, and as the black hole gets created and grows, the surface area of its event horizon increases. As the mass goes up, the surface area goes up, and as more particles pour in, the entropy must rise as well.

It was Bekenstein who first recognized that the information encoded by the infalling particles would, from an external observer’s perspective, appear to get “smeared out” over the surface of the event horizon, enabling a definition of entropy that was proportional to a black hole’s event horizon’s surface area. Today, this is known as the Bekenstein-Hawking entropy: the entropy of a black hole.

Encoded on the surface of the black hole can be bits (or quantum bits, i.e., qubits) of information, proportional to the event horizon’s surface area. When the black hole decays, it decays to a state of thermal radiation. As matter and radiation fall into the black hole, the surface area grows, enabling that information to be successfully encoded. When the black hole decays, entropy will not decrease, but rather will remain constant, as Hawking radiation is an entropy-conserving (adiabatic) process. How or if that information is encoded into the outgoing radiation is not yet determined.

Will that information get destroyed?

This definition was very exciting, but the notion that we had made sense of the Universe — of entropy, information, and black holes — was extremely short-lived. In 1974, just two years after Bekenstein’s earliest work on the topic, Stephen Hawking came along and not only had a spectacular realization, but performed a tremendous calculation to go with it.

His realization was that the standard way of performing quantum field theory calculations made an assumption: that space would, on tiny quantum scales, be treated as though it were flat, unaffected by the General Relativistic curvature of space. However, in the vicinity of a black hole, this wasn’t just a bad approximation, it was a worse approximation than it would be under any other conditions that occurred within our physical Universe.

Instead, Hawking recognized, the calculation needed to be done in a background of curved space, where the background spatial curvature was given by Einstein’s equations and the properties of the black hole in question. Hawking calculated the simplest case — for a black hole with mass only, without electric charge or angular momentum — in 1974, and recognized that the state of the quantum vacuum, or empty space itself, was fundamentally different in curved space, near the black hole’s event horizon, than the state of the quantum vacuum far away from the black hole: where space is flat.

The simulated decay of a black hole not only results in the emission of radiation, but the decay of the central orbiting mass that keeps most objects stable. Black holes are not static objects, but rather change over time. However, black holes formed of different materials should have different information encoded on their event horizons, and it is not understood if or how that information is then encoded in the outgoing Hawking radiation.

That calculation revealed that black holes don’t simply exist, stably, in this curved space, but that the differences in the vacuum near and far away from the event horizon lead to a continuous emission of blackbody radiation: now known as Hawking radiation. This radiation should:

• have a blackbody spectrum,
• be made almost exclusively of massless photons (not one member of particle-antiparticle pairs),
• should radiate at a very low temperature that’s inversely proportional to the mass of the black hole,
• and should evaporate in a time that’s proportional to the mass of the black hole cubed.

This is remarkable, and is a purely quantum effect that we’re now realizing may apply to systems other than black holes as well.

However, it raised a new, troubling issue. If the radiation that comes out of a black hole as it evaporates, this Hawking radiation, is purely blackbody in nature, it should have no preference for:

• matter over antimatter,
• baryons over antibaryons,
• leptons over antileptons,
• one lepton family over another,

or any other metric needed to answer a yes/no question regarding the initial quantum state of the matter that went into creating the black hole in the first place. For the first time, it seems that we’ve encountered a physical system where knowing and measuring all of the information about its “final state” doesn’t, even in principle, allow you to reconstruct the initial state.

When a black hole either forms with a very low mass, or evaporates sufficiently so that only a small amount of mass remains, quantum effects arising from the curved spacetime near the event horizon will cause the black hole to rapidly decay via Hawking radiation. The lower the mass of the black hole, the more rapid the decay is, until the evaporation completes in one last “burst” of energetic radiation.

The core of the black hole information paradox

So where, then, does the information go?

That’s the puzzle: we think that information shouldn’t be able to be destroyed, but if the black hole is evaporating into pure blackbody radiation, then all of that information that went into making the black hole has somehow disappeared.

• It’s possible, of course, that what we think we know about information, entropy, and thermodynamics is not correct, and that black holes really are information-destroying entities.
• It’s also possible, that even if we don’t presently understand the mechanism by which it occurred, that there’s some relationship between — from the perspective of an observer outside the event horizon — the information encoded on the surface of a black hole and the information encoded in the outgoing (Hawking) radiation.
• And, if we’re truly keeping an open mind, it’s possible that something more fundamentally complex is occurring: that the information that goes into making-and-growing a black hole gets “mixed up” somehow in the interior of a black hole, and then is encoded in some non-trivial fashion in the radiation when the black hole itself evaporates.

The event horizon of a black hole is a spherical or spheroidal region from which nothing, not even light, can escape. But outside the event horizon, the black hole is predicted to emit radiation. Hawking’s 1974 work was the first to demonstrate this, but that work has also led to a paradox that has not yet been resolved.

The truth is, despite many declarations over the years that the “black hole information paradox has been resolved,” that nobody knows. Nobody knows whether the information is preserved, whether it’s destroyed or erased, and whether it depends on what occurs in a black hole’s interior or whether it can be completely described from an outside observer’s perspective.

We have mathematical correspondences between what happens on the inside and the outside of a black hole, including an underappreciated fact that takes us beyond the semiclassical approximation (quantum field theory calculations in a background of curved spacetime) used by Hawking: that when radiation comes out of a black hole, it should maintain a quantum mechanical entangled link to the black hole’s interior.

We have devised methods that allow us to map the entropy of a black hole’s interior onto the outgoing radiation that arises due to the Hawking mechanism, which suggests (but does not prove) that we may be approaching a mechanism for understanding how the information that went into creating a black hole gets encoded back into the Universe outside of the black hole’s event horizon.

Unfortunately, we don’t know how to calculate individual bits of information using any of these methods; we only know how to calculate overall “amounts” of information as though we’re putting them on a scale, seeing whether they balance or not. That’s an important step, but it isn’t enough to resolve this paradox.

It’s generally assumed that at some level, gravity will be quantum, just like the other forces. While the semi-classical approximation for computing the decay of black holes involves performing quantum calculations in the classical background of Einstein’s curved space, that approach might not be valid for capturing the full suite of physical behavior that the outgoing radiation possesses, particularly as far as information is concerned.

Certainly, there are other ideas that are playing a major role. String-inspired ideas like complementarity and the AdS/CfT correspondence, as well as the notion of a “firewall” appearing partway through the evaporation process, are considered by many working on the paradox. Others suggest that there are correlations between every quantum of radiation emitted in the Hawking process (similar to entanglement), and that the full suite of those correlations must be understood in order to resolve the paradox. Still others have suggested altering the black hole’s internal and external geometries over the course of the emission of Hawking radiation to attempt to preserve information, while others appeal to whatever strong quantum effects must be present at the interface of quantum physics and relativity: becoming important in the final stages of black hole evaporation.

However, we still do not understand the most important aspects of the paradox: where the information from the particles that create the black hole goes, and how that information — assuming it does get out into the Universe again — actually gets encoded into the outgoing radiation that results when black holes evaporate. Despite whatever claims you may have heard, make no mistake: the black hole information paradox is still an unresolved paradox, and although it’s still an active area of research, no one can be sure what the solution will ultimately be, or what method will eventually lead us to it.