Even “instant” quantum behavior is still limited by the speed of light

If you throw a tennis ball at a solid wall, it will strike the wall and ricochet back at you 100% of the time, just like you’d expect. In physics, a sufficiently strong barrier will prevent any incoming object from passing through it. But at the quantum level, this isn’t strictly true. If you replace a tennis ball with a quantum particle and a solid wall with any quantum mechanical barrier, there’s a finite probability that the particle will actually tunnel through the barrier, where it winds up being detected on the other side. It’s as though you threw the tennis ball at the wall and it went right through, unimpeded by the wall at all.

One of the questions you might seek to ask is whether there’s any delay in the apparent motion of that quantum particle as it moves “through” the barrier via the process of tunneling. In a 2019 experiment, scientists measured exactly that, and found that the tunneling process itself was instantaneous; there was no delay caused by the tunneling process at all. Some have questioned whether this means, in the quantum realm, that it’s possible to violate the speed limit imposed by relativity: the speed of light. Although your intuition might suggest this possibility to you, it turns out not to be the case at all. All processes, even quantum ones, still need to obey the rules of relativity, and can never exceed the speed of light. Here’s how to reconcile the instantaneous nature of quantum tunneling with the fact that no information is ever transmitted faster than the speed of light.

By examining this strobe image of a bouncing ball, you cannot tell for certain whether the ball is moving toward the right and losing energy with each bounce, or whether it’s moving toward the left and getting an energetic kick with each bounce. The laws of physics are symmetric under time-reversal transformations, and yet we only ever perceive time’s arrow as running in one particular (forward) direction. The reason why is not yet known.

When you think of the quantum Universe, chances are you think of tiny, individual particles all zipping around and colliding into one another. This isn’t a bad picture to have in your head, but it doesn’t encapsulate what’s truly going on at a quantum level. One of the counterintuitive aspects of the quantum nature of reality is that treating these quanta as particles, with specific positions and motions at any instant in time, doesn’t fully explain what we observe. We know that there’s a fundamental uncertainty inherent to certain properties (like the positions) of quantum particles, and we can only describe them fully by using a probabilistic description of reality.

What this means is that if you take a single quantum particle, place it down at any one location, and ask “Where is it now?” at some later time, you won’t find it simply by multiplying its speed by the amount of time that’s passed. The quantum nature of this particle means that its position is defined by a wavefunction, not by one specific, well-determined value. Even at the limits of physics, we can only tell you the relative probabilities of where you might find the particle, and only through observation can you determine precisely what that particle’s location actually is.

As time goes on, even for a simple, single particle, the quantum wavefunction that describes its position will spread out, spontaneously, over time. This happens for all quantum particles.

This bizarre, counterintuitive property of quantum physics isn’t a limitation of our measurement equipment, but rather is a fundamental property of our reality and the rules that govern it. Whether you’re talking about:

• a particle at rest,
• a free particle traveling through space,
• a bound particle (like an electron in an atom) that’s restricted as far as where it’s allowed to be,
• or a particle that encounters an obstacle that restricts what quantum states it’s allowed to occupy,

there is no completely deterministic calculation you can do to uncover precisely where that particle is.

All you can calculate is the probability that the particle will be found in a particular location or over a particular interval. Until you make a measurement, which reveals a property such as “position” to whatever measurement uncertainty your measuring device allows, these probabilities are the only guide we have as to where the particle is. There is no such thing as a 100% “certain” position in quantum physics; the Heisenberg uncertainty principle ensures that there will always be a finite, non-zero uncertainty to such a property.

Trajectories of a particle in a box (also called an infinite square well) in classical mechanics (A) and quantum mechanics (B-F). In (A), the particle moves at constant velocity, bouncing back and forth. In (B-F), wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. These stationary (B, C, D) and non-stationary (E, F) states only yield probabilities for the particle, rather than definitive answers for where it will be at a particular time.

There’s an inherent uncertainty relation to position and momentum; that’s the most commonly used example of quantum uncertainty. But there are others as well, including an uncertainty between a particle’s energy and between the time interval over which a particle either exists in a certain quantum state or which you’re attempting to measure its properties. If you’re thinking of this, you might also think that a system that has a probability of tunneling from one side of a quantum barrier (like bound in an atom, or in a false minimum) to the other must have a restriction on how quickly that transition could occur.

Maybe it would depend on the size of the barrier, the thickness of the barrier, or some other factor that was related to its physical properties. After all, in this Universe, everything should be limited by the speed of light.

The simplest setup we can imagine to test this is to take one single particle, like an electron, that’s bound in a restricted system, like a hydrogen atom. There’s a finite, non-zero probability that the electron will spontaneously tunnel to an unbound state. By imaging it with the proper equipment — ultra-fast photons, for instance — you can accurately measure the time interval it takes to tunnel from a bound to an unbound state.

In many physical instances, you can find yourself trapped in a local, false minimum, unable to reach the lowest-energy state, which is known as the true minimum. Whether you receive a kick to hurdle the barrier, which can occur classically, or whether you take the purely quantum mechanical path of quantum tunneling, going from one state to another is always possible so long as no fundamental conservation laws are violated. This is an example of a first-order phase transition, rather than a smooth (second-order) transition without any false minima.

In 2019, that’s precisely what researchers at the Australian Attosecond Science Facility accomplished, finding that this transition, arguably the simplest of electron transitions, takes at most 1.8 attoseconds, or 1.8 × 10-18 s. That means, at the speed of light (299,792,458 m/s), we’re talking about traveling a distance of just 5.4 ångströms. According to Robert Sang, one of the lead researchers:

“There’s a well-defined point where we can start that interaction, and there’s a point where we know where that electron should come out [the interaction itself is] instantaneous. So anything that varies from that time we know that it’s taken that long to go through the barrier… It came out to agree with the theory within experimental uncertainty being consistent with instantaneous tunneling.”

While this has fascinating and profound implications for a variety of practical applications, including, for example, the construction of a quantum-limited transistor, “instantaneous” in this context doesn’t mean that the electron moves from one physical location to another instantaneously, which would be in violation of Einstein’s relativity.

This generic illustration of quantum tunneling assumes there is a high, thin, but finite barrier separating a quantum wavefunction on one side of the x-axis from the other. While most of the wavefunction, and hence the probability of the field/particle that it’s a proxy for, reflects and remains on the original side, there is a finite, non-zero probability of tunneling through to the other side of the barrier. This phenomenon must be explicable in all interpretations of quantum mechanics.

It isn’t as though at one instant you can say “This particle is over there” and then, some tiny amount of time later, you can say “This particle is now located here instead.” If you could do that, you could simply take the measured change-in-distance and divide it by the change-in-time that occurred; if that number came out to a number greater than 299,792,458 m/s, you’d conclude that you had exceeded the speed of light. The experiment that was performed with an electron within a hydrogen atom, which is remarkable for how precise and clean it was in only involving a single particle in a single, bound system, was not able to make that critical measurements.

All it could do was demonstrate that there’s no fundamental “quantum delay” in the tunneling transition from a bound state to an unbound state. Nevertheless, experiments like these are useful for exposing how physicists have managed to exploit a many-particle system in order to create the illusion of something traveling faster than light: a result which gets misreported every few years in the popular media.

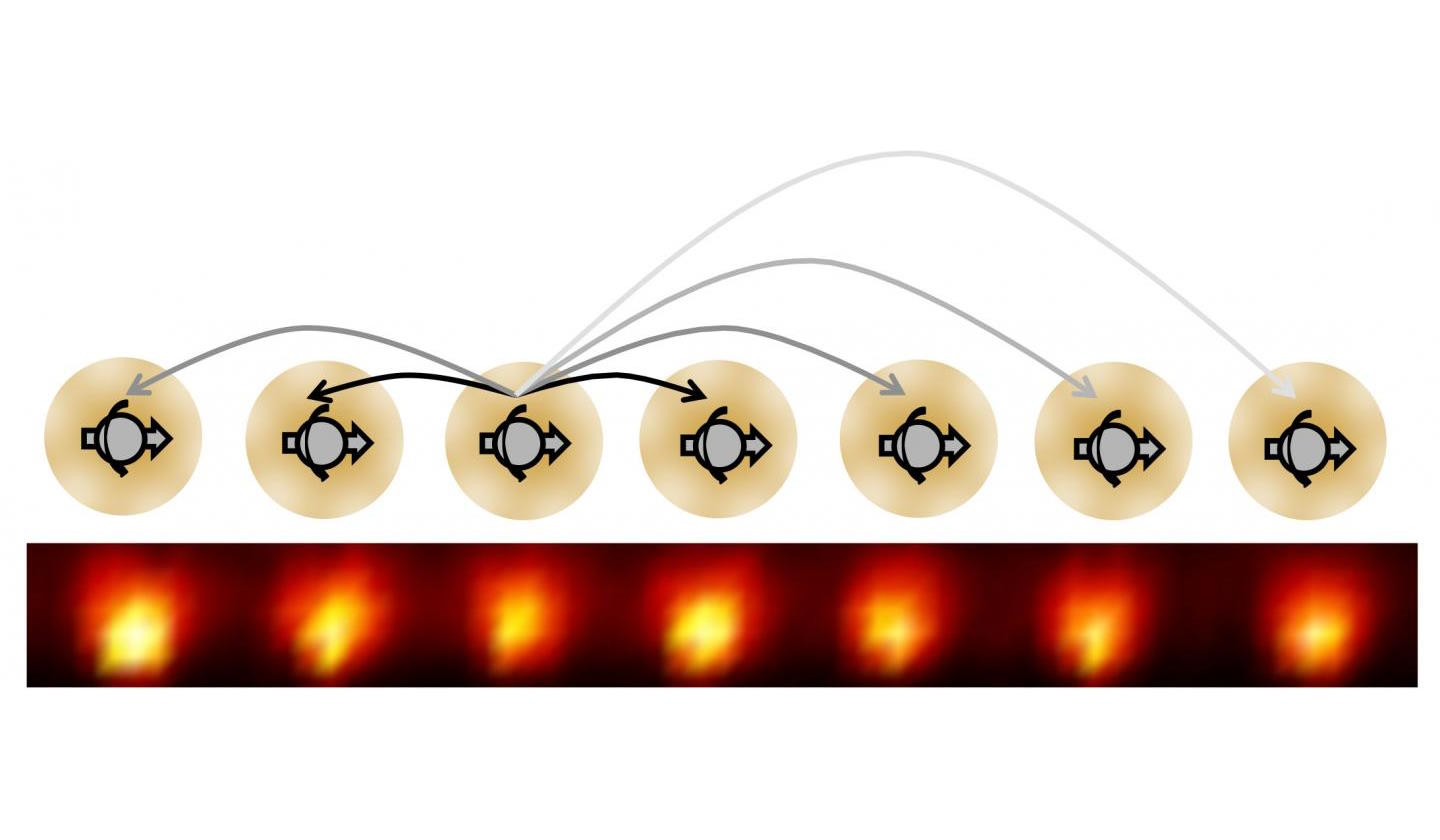
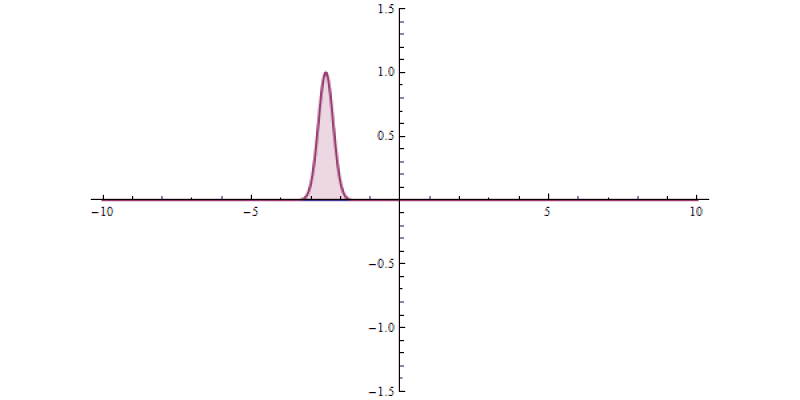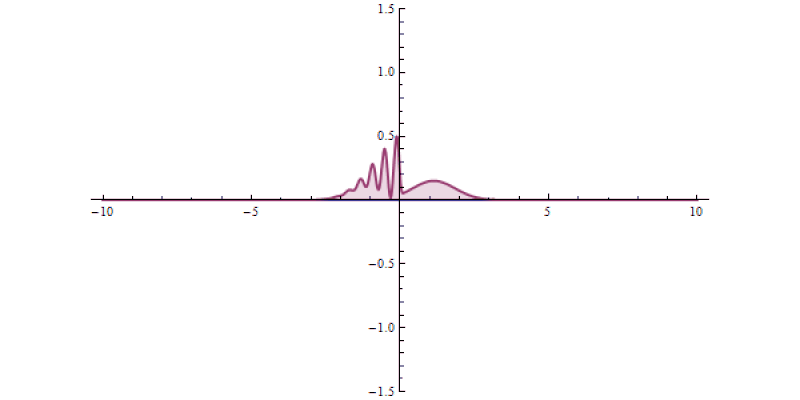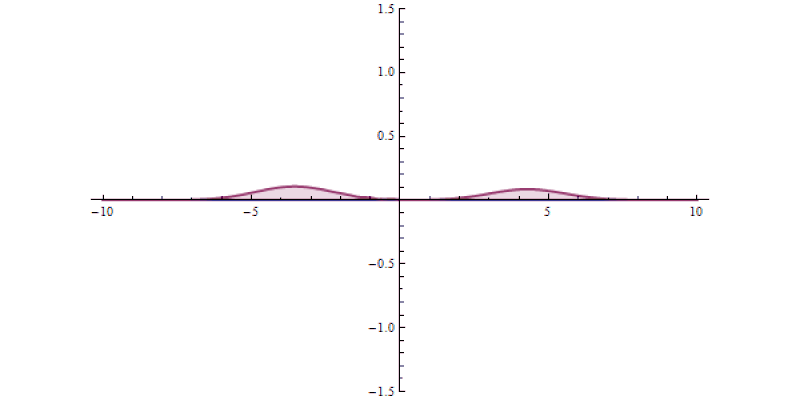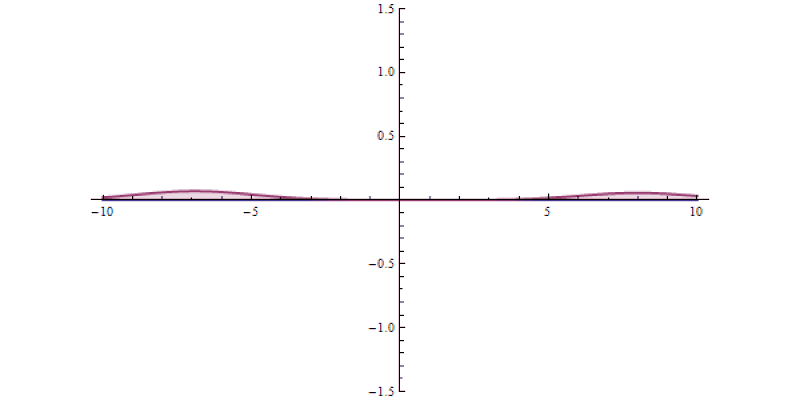
To illustrate this, imagine you’ve got a set of quantum particles, bunched together into a tight pulse, tunneling or otherwise traveling through a barrier of some sort.

By firing a pulse of light at a semi-transparent/semi-reflective thin medium, researchers can measure the time it must take for these photons to tunnel through the barrier to the other side. Although the step of tunneling itself may be instantaneous, the traveling particles are still limited by the speed of light. By taking high-speed images of this light pulse, we can construct a movie that appears continuous.

It’s truly remarkable at how successful we’ve become at imaging pulses that move at speeds that approach or even equal the speed of light, thanks to novel techniques and technologies. Because we have these advanced imaging capabilities today, we can use multiple separate measurements, over time, to illuminate your understanding of the quantum Universe, and to prevent you from being fooled by this type of erroneous “faster-than-light” claim.

Step 1: The first thing you’ll want to measure, as precisely as possible, is where this pulse of physical quanta is located, in space and at a certain moment in time, before a quantum barrier is ever encountered.

When you create a pulse of particles, whether those particles are massive or massless (like light itself), there is always a distribution in space and time inherent to those particles. While you may not be able to measure this distribution to infinite, arbitrary precision, your measurement apparatus is capable of measuring a position and a time for even quantum particles simultaneously.

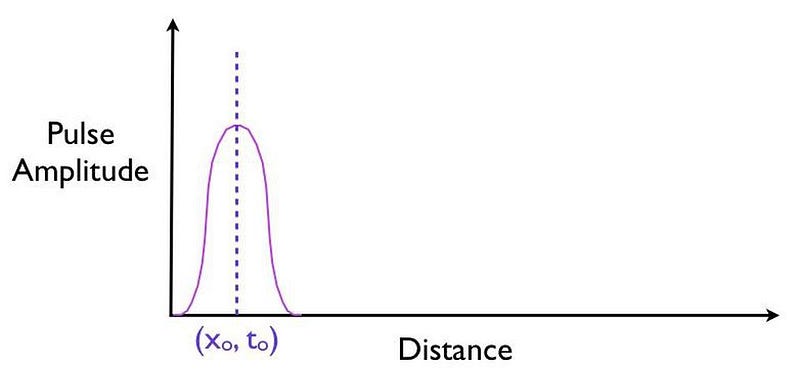
Step 2: The next thing you’ll want to do, before making the next measurement, is to calculate precisely where-and-when you’d expect the pulse of quanta to arrive under the assumption that the pulse were to move at the speed of light and were to successfully tunnel through the barrier in front of it.

Naively, if you sent particles from one location to another without a barrier or something to filter them out in between, you’d expect they would arrive at your destination in a predictable amount of time that was set (or at least limited) by the speed of light. This is a straightforward calculation to perform: simply “translate” your particles forward by a distance that corresponds to the light-travel distance over the amount of time between the initial and final measurements.

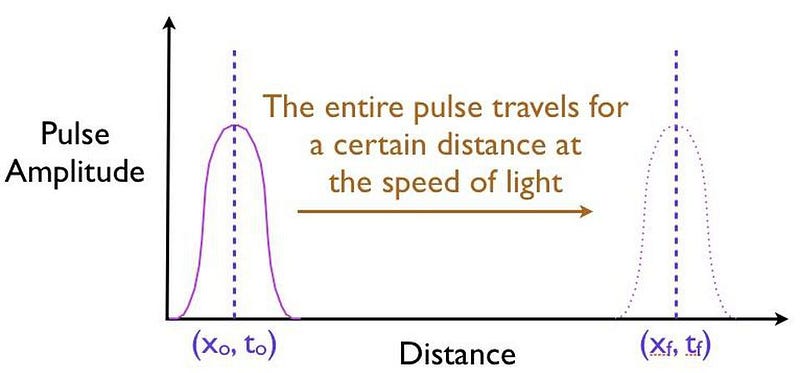
Step 3: Now, you’ll want to make that measurement for precisely where the pulse is located at a later instant in time, after it successfully tunnels through the barrier.

But, when you make that measurement, you shouldn’t be surprised if you learn that the pulse that you detect on the other side of the barrier — the pulse that must’ve tunneled through the barrier in order to get there — might appear to have moved faster than the speed of light would seem to permit!

If all you did was measure the start position, time and end position, and time of a set of particles that were sent toward and wound up passing through a quantum barrier, you might (falsely) conclude that these arriving particles had traveled faster than the speed of light. Don’t worry, they didn’t; you’re not observing the full suite of particles, only the (possibly weighted) portion that made it through your quantum barrier.

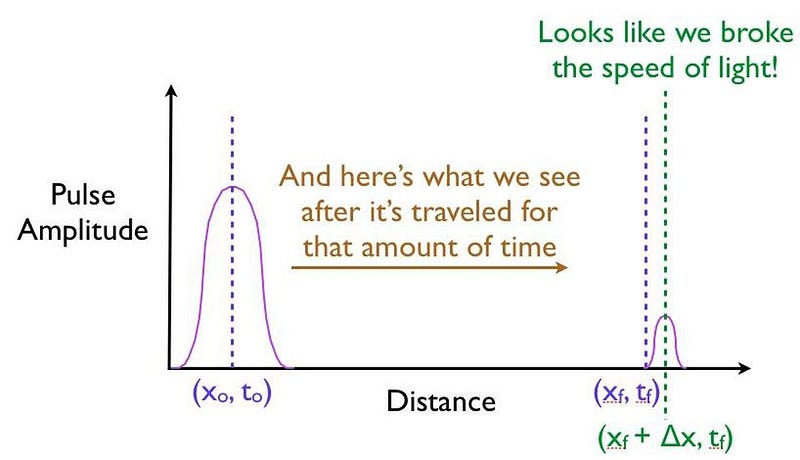
This is a tricky situation, as you might think, based on what you just read about the speed of quantum tunneling being instantaneous, that this means that particles can travel infinitely fast, breaking the speed of light, through a quantum mechanical barrier of finite, non-zero thickness.

That’s the misinterpretation that always crops up, and how people fool themselves (and unscrupulous news organizations try to fool you) into thinking they’re breaking the speed of light.

But that’s not what’s happening here, or in any of these so-called “faster-than-light” demonstrations. Instead, all that’s happening here is that only a portion of the quantum particles found in the pulse manage to successfully tunnel through the barrier. The majority of the particles do what a (classical) tennis ball would do: they bounce back, failing to arrive at the destination. The “trick” to fooling yourself into believing that you’ve created a faster-than-light system is that it’s possible to front-load which particles make it through the barrier, preferentially cutting off the particles in the back of the pulse.

If you do this without being sufficiently careful, you’ll falsely measure a faster-than-light speed for the overall pulse, even though no individual particle actually ever exceeds the speed of light.

If you were to somehow track the individual motion of each and every particle that you launched toward your destination, you’d find that the ones that made it were simply part of the front-end of the initial pulse, and that no actual particles were traveling faster than light itself.

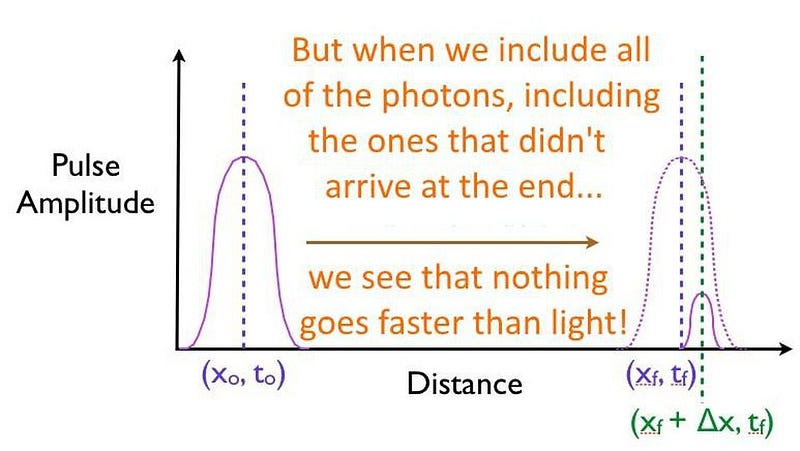
So what does it mean, then, for the researchers to assert that quantum tunneling is an instantaneous process that occurs without any delay?

Simply that the actual process of tunneling itself, where the transition occurs from being in a bound state on one side of a quantum barrier to an unbound state on the other side, doesn’t take any extra, additional time on top of all the other physical effects. It means that there’s no inherent “quantum delay” for the process of tunneling to occur.

But as the particles in your system move a finite distance over a finite amount of time, they’re still fundamentally limited by Einstein’s relativity. This restriction applies to each and every particle, under all circumstances, with no exceptions. It’s an incredible feat that scientists have now measured the speed of a quantum transition from an electron to go from a bound state to an unbound state directly, for a single particle, determining that there is no delay occurring that’s inherent to the quantum tunneling process itself. However, at no point is any quantum particle actually traveling faster than light. That’s a phenomenon that’s restricted, at least as far as we know, to the realm of science fiction alone.