In A Quantum Universe, Even Mass Is Uncertain

In the quantum world of the unstable, even identical particles don’t have identical masses.

In the microscopic world of the quantum particle, there are certain rules that are wholly unfamiliar to us on a macroscopic scale. If you measure a particle’s position and ask “where are you,” the more accurately you learn the answer, you’ll fundamentally know its motion, or its momentum, less well. Other properties, however, like electric charge, remain perfectly well-known at all times, regardless of what else you measure. For purely stable particles, whether elementary or composite (including electrons and protons), mass is one of those perfectly-known properties. If you know the mass of one electron under one set of conditions, you know it for all electrons everywhere in the Universe. But this isn’t the case for all the particles we know of. The shorter-lived an unstable particle is, the more uncertain its mass is. This isn’t just a hypothesized effect, but rather one that’s been experimentally observed and verified for decades.

From a theoretical standpoint, quantum uncertainty ought to play a role wherever two physical properties that are related in a certain way exist. That particular relationship is one that we call “non-commutative,” and it’s weird to think about. If I measure your position (where you are), for example, and then I measure your momentum (a measure of your motion), you’d expect that I’d get the same results as if I measured first your momentum and then your position. In classical physics, all variables commute: it doesn’t matter whether you measure position and then momentum, or momentum and then position. You get the same answers either way. But in quantum physics, there’s an inherent uncertainty that arises, and measuring position and then momentum is fundamentally different from measuring momentum and then position.

It’s as though I told you that “3 + 4” was somehow fundamentally different than “4 + 3”. In the quantum Universe, this is a fundamental and unavoidable property known as Heisenberg uncertainty, and it tells you that for quantities like position (Δx) and momentum (Δp), there’s this inherent uncertainty between them, and hence an inherent uncertainty in each variable. This isn’t restricted to position and momentum, either. There are plenty of physical quantities out there — often for esoteric reasons in quantum physics — that have that same uncertainty relation between them. This happens for every pair of conjugate variables we have, just like position and momentum are. They include:

• Energy (ΔE) and time (Δt),
• Electric potential, or voltage (Δφ) and free electric charge (Δq),
• Angular momentum (ΔL) and orientation, or angular position (Δθ),

along with many others. It tells you that these two quantities, multiplied together, have to be greater than or equal to some finite value: ℏ/2.

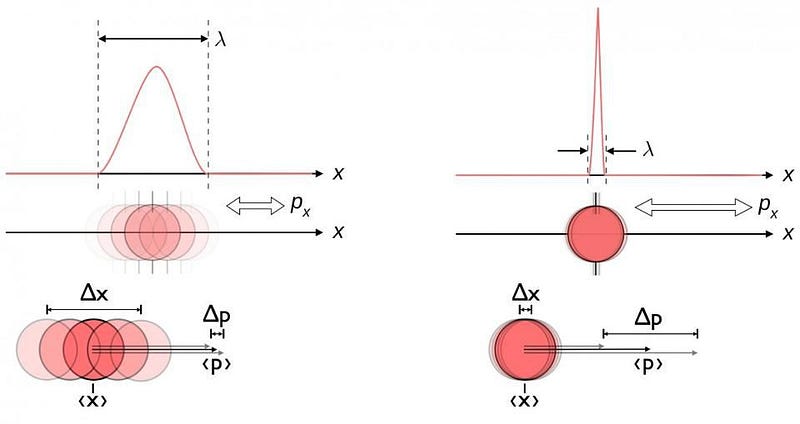
While position and momentum are the usual examples we talk about, in this case, it’s the energy-and-time relation that leads to the bizarre and confusing behavior. If a particle is completely stable, then the uncertainty in its lifetime doesn’t really matter: any finite uncertainty (Δt) added on to an infinite lifetime is inconsequential. But if a particle is unstable, then there’s an uncertainty in how long it survives that’s roughly equal to its mean lifetime: Δt. That means there’s an inherent uncertainty to its energy as well; using our uncertainty formula, it tells us that if you multiply your energy uncertainty (ΔE) by your time uncertainty (Δt), it has to be greater than or equal to ℏ/2.

And the shorter your particle’s lifetime is, the larger your energy uncertainty needs to be.

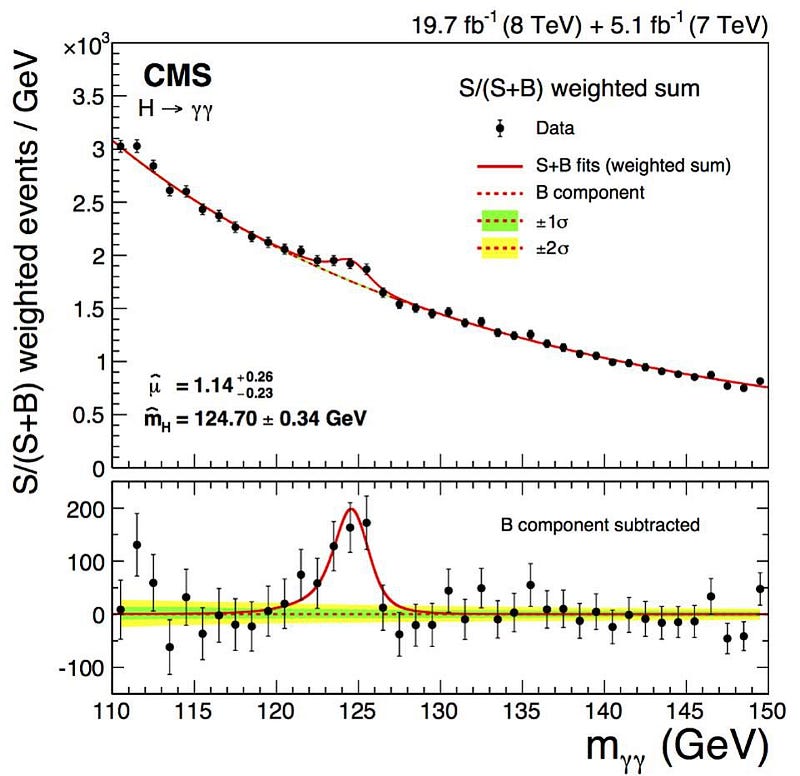
But an uncertainty in energy, for a particle, means there must be an uncertainty inherent in its mass, too, since E = mc². If it has a bigger energy uncertainty, it has a bigger mass uncertainty, and the shorter-lived a particle is, the bigger its mass uncertainty has to be. A lot of people noticed, when they first detected the Higgs boson, that it showed up as a “bump” in the data (above). If the Higgs boson were, instead always the same exact, single mass, we’d reconstruct it to be an infinitely narrow “spike,” where the only uncertainty came from our own measurements.

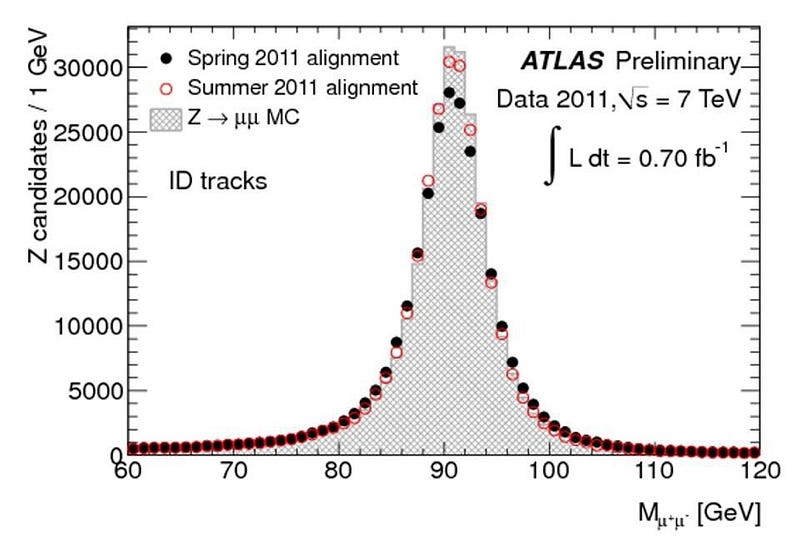
Now, it’s true that there are measurement/detector uncertainties, and these do play a role. But many particles — like the Higgs boson, the Z boson, the W+ and W- bosons, and the top quark — are incredibly short-lived, with lifetimes on the order of 10^-24 seconds! (Or in the case of the top quark, even less than that.) Every time you create a Higgs particle, it could be (in terms of energy) 124.5 GeV, 125.0 GeV, 125.5 GeV, or 126.0 GeV, or anywhere in between. When you create a Z boson, it could range anywhere from about 88 GeV to 94 GeV. And, most remarkably, when you create a top quark, it could have a rest mass of anywhere from about 165 GeV all the way up to over 180 GeV: the largest range of any known elementary particle.

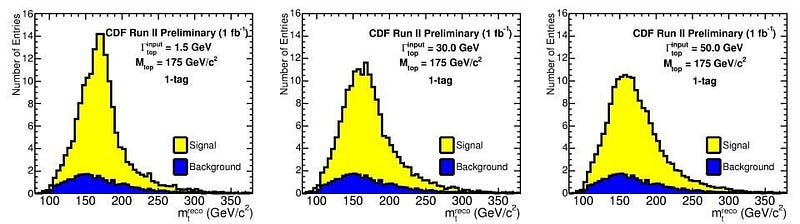
This means that, literally, when you create one of these particles and measure how much energy it had, it’s fundamentally and inherently different than the next particle of exactly the same typeyou’ll create. This is a non-intuitive property of quantum particles that only comes up when they’re unstable. Any electron that you create is indistinguishable from any other electron in the Universe, but each top quark that exists will have its own unique set of particles and energies that decay from it, with an uncertainty inherent to all of their properties, including their total mass/energy.

It’s one of the most remarkable and counterintuitive results of the quantum Universe, that every unstable particle that you make has an inherent uncertainty to the most seemingly fundamental property of all: mass. You can know what the average mass of a typical particle of any particular type, and you can measure its width, which is directly related to its mean lifetime through the Heisenberg uncertainty principle. But every time you create one new particle, there’s no way to know what its actual mass will be; all you can do is calculate the probabilities of having a varieties of masses. In order to know for sure, all you can do is measure what comes out and reconstruct what actually existed. Quantum uncertainty, first seen for position and momentum, can now be convincingly stated to extend all the way to the rest energy of a fundamental particle. In a quantum Universe, even mass itself isn’t set in stone.