Overcoming the last “impossible” step in making supermassive black holes

- The most massive black holes in the Universe weigh in at billions or even tens of billions of solar masses.
- The only way to get that large is by incorporating mergers, but the longstanding “final parsec problem” has always stood in the way of this scenario.
- After years of contentious debate, the final parsec problem is no longer a problem; here’s how to solve it.
At the center of practically every massive galaxy in the Universe is the same type of structure: a supermassive black hole. Ranging from a few million solar masses up to tens of billions of solar masses, these astrophysical engines are the most extreme objects known to humanity. Powering the tremendous jets and ejecta associated with quasars, blazars, and active galactic nuclei, these objects are at least partially responsible for shaping and determining the fates of the host galaxies of which they’re part.
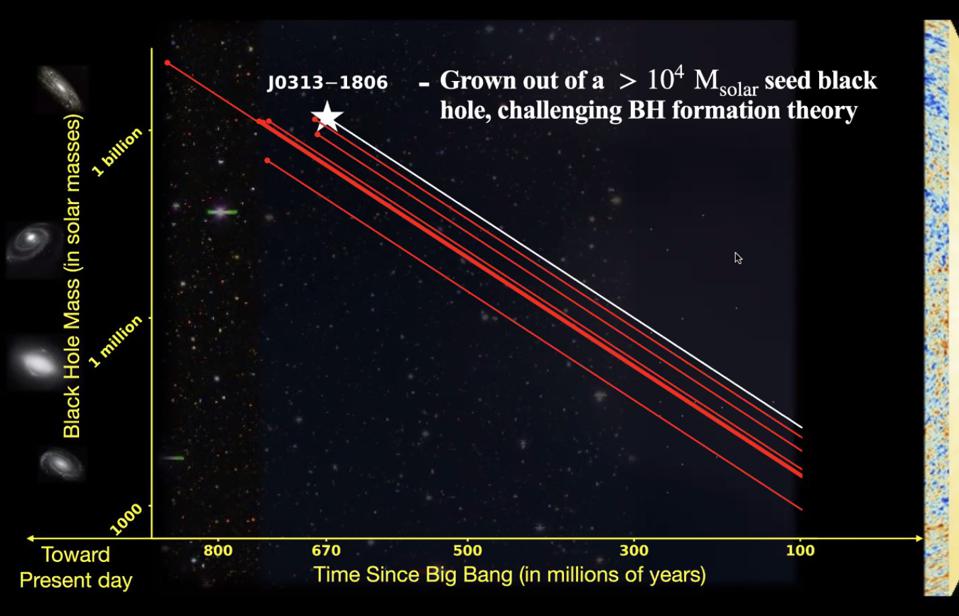
But how are these extreme objects made? We have a very simple and straightforward story for the creation of the “other” major class of black holes: stellar mass black holes. When a large, massive star reaches the end of its life, it can die in either a core-collapse supernova or it can directly collapse in its entirety: giving rise to a black hole of tens or, quite possibly, hundreds of masses. But how do we get them to grow to be billions of solar masses in heft, particularly so early on in the history of the Universe, where the earliest quasars show that they were this huge very early on? For a long time, it seemed impossible, owing to the “final parsec problem.” Here’s why, at last, that’s not a problem anymore.

Credit: ESO/MPE
At the start of the hot Big Bang, there was nothing even resembling a black hole. There were no large, collapsed masses; no tremendously large overdensities; nothing to even serve as the seeds of these runaway structures. All we had were regions — on all cosmic distance scales, from cosmic to subatomic — where the overall density differed slightly from the average density.
Yes, it’s the initially overdense regions that will eventually grow into the modern-day structure we see in the Universe:
- planets
- stars
- galaxies
- clusters of galaxies
- supermassive black holes
But it takes a very long time for them to get there. The reason is simple: We’ve measured the magnitude of fluctuations that existed very early in the Universe’s history and it’s very small. Typically, a region of space will depart from the average density by just 0.003%, with an extreme, one-in-a-few-million overdensity being perhaps 0.015% denser than average. These small seeds will grow into interesting structure eventually, but it will take time: tens or hundreds of millions of years to even form the very first stars of all.

Credit: Nicole Rager Fuller / NSF
Fortunately, that should be completely sufficient to start of the process of growing a supermassive black hole. Once enough mass accrues in one place, gravitation will cause it to begin to collapse. With only hydrogen and helium present at this early stage, the amount of mass required to trigger that collapse is much greater than it is today, and the stars that form as a result will also be much more massive. Whereas the average star that forms today is only about 40% the mass of the Sun, the average “first star” in the Universe is anticipated to be more than ten times as massive as our Sun.
When stars are that massive, their lifetimes are very short: only a few tens of millions of years. In addition, the most massive stars that form will be many hundreds — perhaps even thousands — of times the mass of our Sun, and they might live for only one or two million years before evolving into black holes. Once you have a “seed” black hole like this, which you could potentially form when the Universe is merely 50-200 million years old, it can grow by accreting matter at the maximum rate possible: the Eddington limit. If we do this, we can almost, but not quite, get black holes to grow to the sizes we see in a fast enough time. Almost, but not quite.
Credit: F. Wang, image taken at AAS237
But that doesn’t mean forming or growing these supermassive black holes is a problem, because there’s a major ingredient we’ve left out: mergers and the formation of large-scale structure. Sure, the very first stars might give rise to black holes, and those black holes could then grow, but they don’t do so in isolation. When stars form, they form in clusters, frequently with hundreds, thousands, or even greater numbers of them present all at once.
When the first stars form, they do so all across the Universe: in initially overdense regions near and far, no matter where you begin.
And as the Universe ages, it expands but also gravitates. These early star clusters merge together, forming proto-galaxies and eventually full-fledged galaxies. The combination of inflowing matter from the surrounding spatial regions and mergers, both major and minor ones, can bring many of these black holes together into the same post-merger galaxy.

Credit : NASA; Z. Levay and R. van der Marel, STScI; T. Hallas; A. Mellinger
Now, here’s where the real fun begins. If we can get these numerous black holes of varying sizes and masses — in a variety of stages of growth and evolution — to all meet up in the galactic center and merge together, we’ll have no problem forming a supermassive black hole. But if there’s some phenomenon preventing them from meeting up, merging together, or otherwise growing to the necessarily large masses they must possess in a short enough amount of time, we’d run into trouble. We might even conclude, as some have said in recent years, that these supermassive black holes might well be considered “impossible” in some sense.
The first step is pretty easy. When galaxies merge, they’re full of gas, dust, and stars, in addition to the black holes and whatever dark matter may be present. When these black holes travel through this material, relative to one another, the material gets gravitationally scattered in all directions, which effectively slows these black holes down. In simulation after simulation, this typically gets the black holes relatively close together: within about 1-to-10 light-years of one another. This braking process is caused by a phenomenon we call dynamical friction, and will leave us with two black holes orbiting one another at this relatively small cosmic distance.

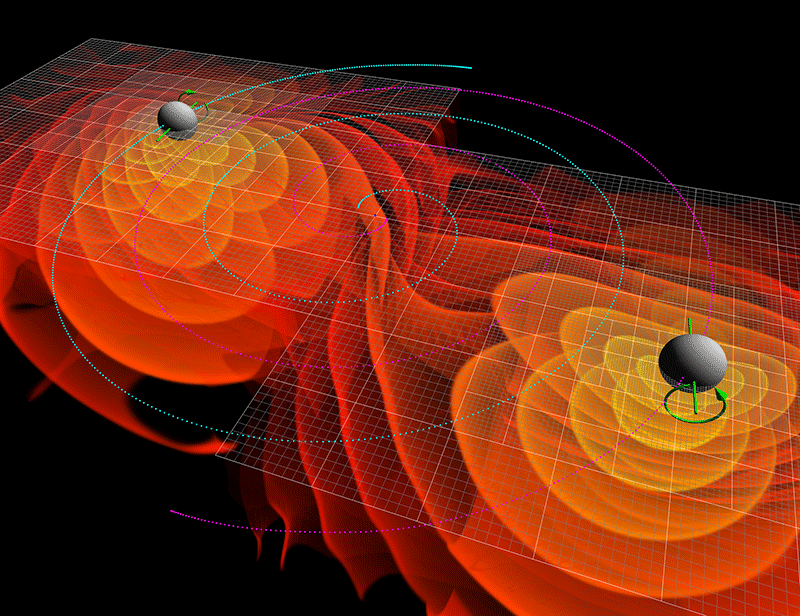
The last step is also pretty easy: the gravitational inspiral and merger of two bound, mutually orbiting masses. One of the greatest scientific discoveries of the last decade has been the identification of inspiraling and merging black holes by gravitational wave detectors, such as LIGO and Virgo. Whenever any two masses orbit one another, the act of each mass traveling through space causes the curvature of that space to change, while the motion of each mass through that region where the curvature is itself changing leads to the emission of gravitational radiation.
These ripples in spacetime, also known as gravitational waves, carry energy away from the system, leading to orbital decay, inspiral, and, eventually, a merger.
For any system of two black holes, based solely on their masses and their initial orbital distance from one another, we can calculate the timescale required for them to merge together. If you want to grow supermassive black holes from these progenitor candidates, you simply need to get them to within about 0.01 light-years of one another. Closer than that, and the Universe provides you with ample time for gravitational waves to do their thing, and for your black holes to merge together.
Credit: C. Henze/NASA Ames Research Center
For years, these two pieces of the puzzle were known, but the critical intermediate step was missing. When galaxies merge together, the two largest black holes will sink to the center and begin orbiting one another. But by the time they’re just a handful of light-years away from one another, all of that intervening matter is gone. Without stars, gas, dust, or other massive objects in there, dynamical friction can take us no closer.
But unless we get much closer first, by about a factor of ~500 or so, gravitational waves won’t lead to those black holes merging together. They’d still be hanging out there even today, a few light-years apart, having failed to merge.
This is why the final parsec problem was considered to pose such a difficulty for theories of supermassive black hole formation. If you can’t fill in that critical in-between step — of going from a too-wide orbit to one narrow enough where a black hole-black hole merger will occur in a reasonable time — then you don’t have a successful explanation for how these supermassive black holes actually form. Fortunately, there are factors we haven’t considered that can fill that gap.

Credit: NASA/JPL-Caltech
One important factor is this: other masses exist! There are clumps of matter of all sorts — stars, stellar corpses, planets, gas clouds, globular clusters, plasma flows, supernova ejecta, etc. — that will migrate down toward the galactic center, and that will eventually pass close to the inspiraling black holes. When they do, a fascinating phenomenon comes into play: violent relaxation.
Whenever you have multiple masses in a gravitational dance, the following will inevitably occur:
- These masses will all mutually gravitationally interact.
- These interactions will impart “kicks,” or changes in momentum, to each of the masses.
- The smallest masses, when they receive appreciable changes in momentum, receive large changes to their velocity.
- This either kicks the small masses to higher, more loosely-bound orbits, or may even eject them entirely.
- The momentum and angular momentum they carry away comes out of the entire system, leaving the remaining masses more tightly bound.
Although violent relaxation is more commonly applied to systems of stars, like star clusters and elliptical galaxies, it works equally well for any system of masses interacting under the force of gravity.

Credit: S5 Collaboration/James Josephides (Swinburne Astronomy Productions)
There are other contributing factors that can make it easier for supermassive black holes to form. This violent relaxation process should also occur early on: all the way back when the first black holes are forming from the first stars. If the initial star cluster is massive enough, this process could yield seed black holes between 10,000 and 1,000,000 solar masses before these clusters even begin merging into proto-galaxies.
The Eddington limit, or the maximum rate at which black holes can grow, is specifically calculated for a spherically symmetric distribution of matter accreting onto an object. But real structures in the Universe, and particularly structures made out of normal, baryonic matter, are highly asymmetric when compared to a sphere. As a result, super-Eddington accretion should actually be the norm when it comes to the growth of supermassive black holes.
And finally, just by looking at the central supermassive black hole in our own galaxy, Sagittarius A*, we can see that its X-ray emission varies tremendously over time. There are flaring periods and quiet periods; outbursts and silence. This teaches us that matter is constantly, but not continuously, falling and flowing onto the black hole, where it gets accelerated and we see the electromagnetic consequences. If it’s happening here, now, then it’s probably happening elsewhere and often. This can either lead to additional violent relaxation or, alternately, a restart to the dynamical friction process every time it occurs.

Credit: NASA/CXC/Amherst College/D.Haggard et al.
For a long time, it was thought that the story of supermassive black holes would be simple and straightforward. You’d form the first stars, they’d die and make black holes, those black holes would grow, and then you’d wind up with the supermassive black holes we see today. With today’s knowledge, we can definitively state that that picture is too simple and naive to work.
However, by folding in just a few additional, more realistic factors, supermassive black hole formation no longer appears to be an impossibility. By recognizing the importance and ubiquity of mergers, both black hole seeds and more mature supermassive black holes could grow to many times their original size in a short amount of time. The combination of dynamical friction as well as continuously infalling and interloping matter can bring multiple black holes within inspiral-and-merger distance on completely adequate timescales. In the cosmic blink of an eye, there are supermassive black holes at the center of every large, modern galaxy.
There are many more pieces of the story still to be uncovered, but this much is clear: the final parsec problem is no longer an “impossible” problem to solve. Binary supermassive black holes may yet be more common than we know them to be at present, as future observatories like Lynx may yet unveil. But when we see a single, supermassive black hole at the center of a galaxy, there’s no longer a reason to doubt that such objects can exist within our Universe as we know it. What we see really is what we get, and it’s no longer an unsolved mystery that these objects formed at all.