How flat can a planet be?

The Earth is round, Kyrie Irving. But not every world needs to be.

“‘I’ll follow him to the ends of the earth,’ she sobbed. Yes, darling. But the earth doesn’t have any ends.” –Tom Robbins

We know that the Earth isn’t flat, and have known this for hundreds of years. There are many ways to demonstrate this, from ships’ masts disappearing as they sail out over the horizon, to your ability to see farther at higher altitudes, to the longer shadows cast by the Sun at higher latitudes, to measuring the shape of the Moon’s shadow on the Earth during a solar eclipse, to actually going to space and seeing the shape of the Earth for yourself.

But just because the Earth isn’t flat doesn’t necessarily mean a planet couldn’t be. In fact, there are many observations that we make that would be consistent with a flat, circular Earth.

So how close could we actually get to a flat planet? One strategy would be to take a solid slab of material — stone, steel, or something even harder like diamond or graphene — and build the largest flat disk you could. If you used conventional materials like this, you could create a thin, flat disk many hundreds of kilometers in radius that was stable. In other words, you could make a flat world that was larger than any object in our asteroid belt, and possibly even nearly the size of our Moon.

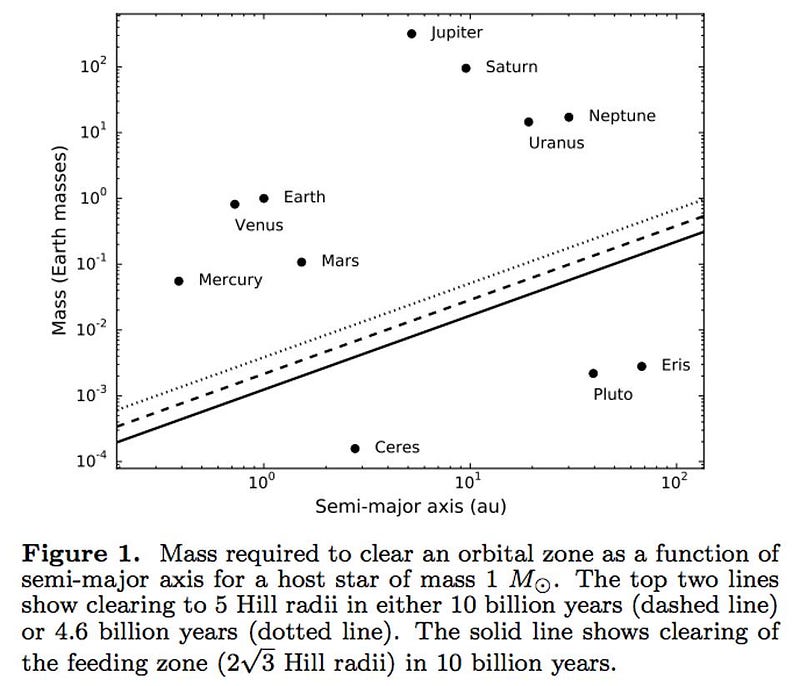
But it wouldn’t be a planet if you did it that way. Back in 2006, we famously set forth the three criteria for defining a planet. (That definition has since been extended to exoplanets, too!) In order to be a planet, a world:

1. must be in orbit around the Sun (and not any other body like another planet),
2. must have sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium shape (round, or oblate/prolate in the case of a rapid rotation), and
3. must clear the neighborhood around its orbit (so that there are no other comparably large bodies also in/near its orbit).

That second part of the definition is what fails for our specially-created flat, thin world. If it isn’t massive enough to pull itself into hydrostatic equilibrium, it can’t be classified as a planet.

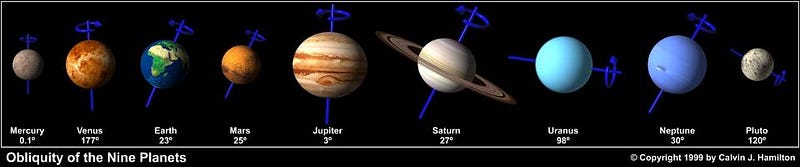
But there is a way to create a relatively flat planet: have it spin. Here on Earth, our planet is a relatively slow spinner: it takes 24 hours for us to rotate a full 360°. This means that a person living on the equator, the maximal distance from the Earth’s axis of rotation, experiences an extra speed of 464 meters per second (about 1,000 miles per hour) compared to someone at the poles. This extra speed affects the entire shape of the Earth, and causes it to elongate into a shape known as an oblate spheroid: a near-perfect sphere that’s flattened at the poles and elongated at the equator.

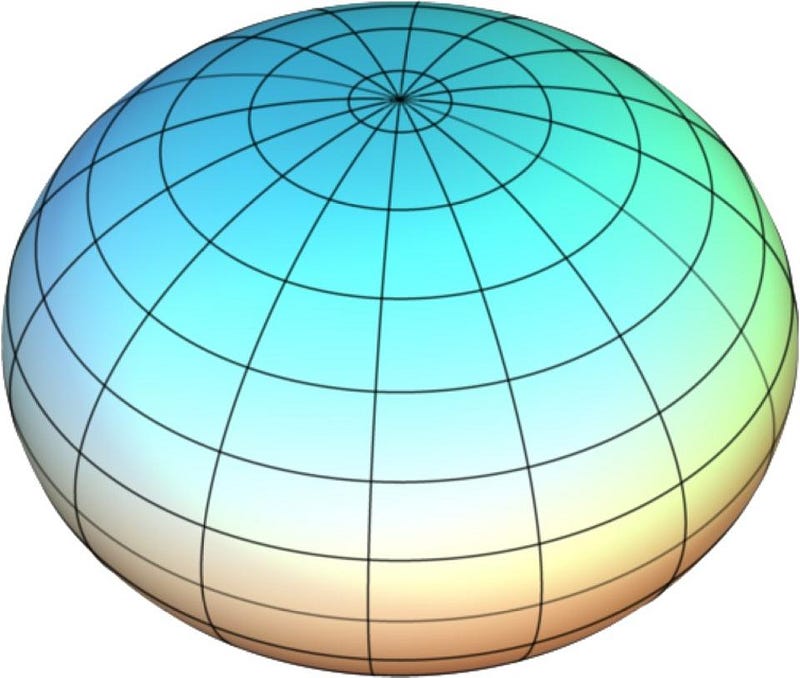
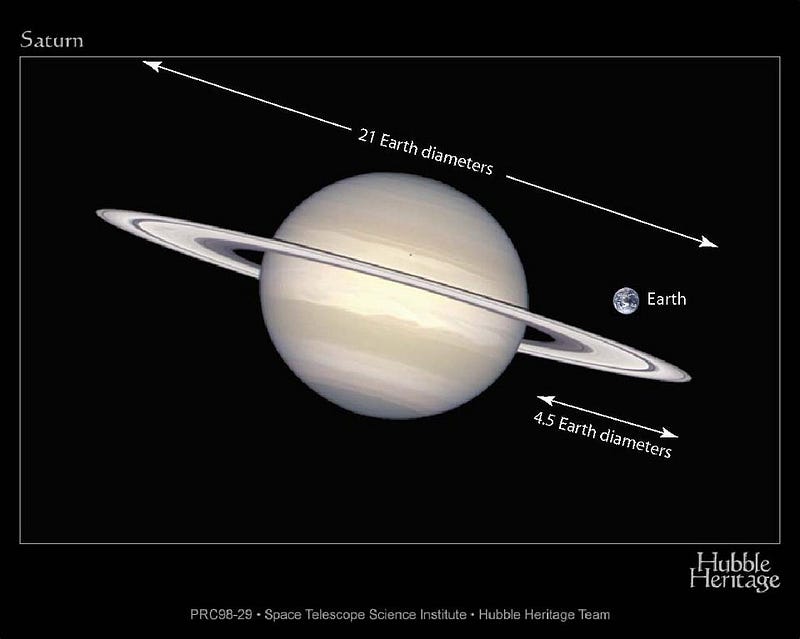
The diameter of the Earth at the equator is 12,756 km, while at the poles its only 12,714 km. You are 21 kilometers closer to the center of the Earth standing at the North Pole than you are at the equator. This doesn’t seem like much, but there are worlds out there that rotate far faster. The gas giants all rotate quite quickly, with Saturn’s poles compressed by 10% relative to its equator.

But that isn’t the limit. According to physics you can have a much flatter world. We had never seen one when all we knew were the eight planets, but as we’ve discovered massive asteroids and worlds in the Kuiper belt, we’ve met some incredible cosmic oddities. The record holder? The massive Kuiper belt object Haumea, whose equatorial diameter along its long axis is twice as large as its shortest axis. This 2:1 ratio is the most extreme world in hydrostatic equilibrium that we know of.

Scientists believe it was a collision that created Haumea’s rapid rotation, along with its two known moons: Hiʻiaka and Namaka. The larger of the two, Hiʻiaka, has a strong gravitational influence on Haumea, further complicating the system. Haumea isn’t simply a world with an equatorial bulge and compressed poles; it has three separate axes of various lengths, making it a triaxial ellipsoid.

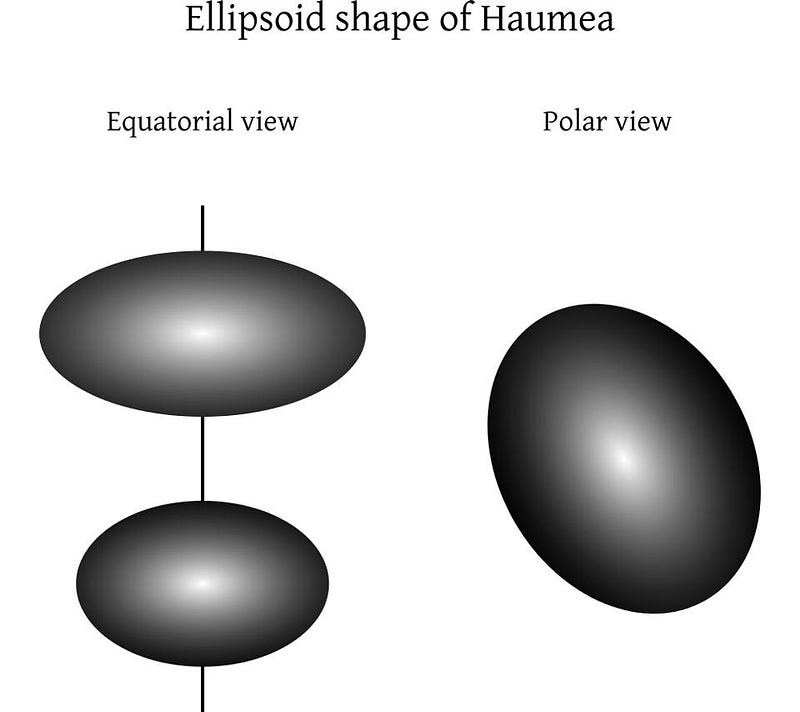
In other words, Haumea is only the most extreme example we know of so far, but in theory, a world could be even flatter. The denser a planet is and the faster it rotates, the flatter it gets. In principle, the limit for flatness is given by whether an object could spin fast enough to cause its equatorial particles to be flung off the world and into outer space, overcoming the planet’s gravitational attraction. For a planet like Earth, we could reach a maximum flattening ratio of about 3:1 before our equator began to escape into space; a planet made entirely of uranium could perhaps reach a 5:1 ratio.

The flatter you get, the harder it is to maintain a rigid world, as the internal forces work to create friction and differential rotation at the outer layers. Just as the outer portions of Saturn’s rings rotate more slowly than the inner ring particles, a flattened planet would have to contend with the same forces. In theory, you can have a much flatter planet than Earth, but there’s no world that obeys the laws of physics that you’d ever confuse with being truly flat!

This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!